Черняк О.І. та ін. Економетрика

31

Квар

тал

Випуск,

тис грн, y

Капітал

,

тис грн,

x

2002/

Q2

129 787

2002/

QЗ

131 809

2002/

Q4

140 812

1. Побудуйте регресію вигляду

ttt

yx



  .

2.

Побудуйте надійні інтервали для коефіцієнтів моделі з рівнем надійності 99 %.

3.

Перевірте модель на адекватність із рівнем надійності 95 %.

4.

Визначте, на скільки зросте випуск підприємства при збільшенні розміру

встаткування на 3 %.

5.

Визначте, на скільки зросте випуск підприємства при збільшенні розміру

встаткування на 1,2 млн грн.

Задача 1.16. Відома інформація про дохід підприємства у млн грн, y , і відношення

його капіталу до кількості працівників





K

L

:

y K/L

2,

263

12,

116

2,

266

12,

137

2,

284

12,

259

2,

300

12,

364

2,

367

12,

805

2,

412

13,

109

2,

442

13,

313

2,

508

13,

757

2,

538

13,

960

2,

585

14,

280

2,

653

14,

745

2,

667

14,

845

2,

670

14,

859

2,

686

14,

975

2,

698

15,

056

2,

728

15,

259

2,

749

15,

409

2,

795

15,

728

2,

896

16,

429

2, 16,

32

y K/L

945 772

3,

245

18,

906

3,

268

19,

077

3,

284

19,

193

3,

297

19,

282

3,

350

19,

668

1. Оцініть функцію Солоу





tt

K

y

L



  .

2.

Побудуйте надійні інтервали для коефіцієнтів моделі з рівнем надійності 95 %.

3.

Перевірте модель на адекватність із рівнем надійності 90 %.

4.

Визначте, на скільки зросте дохід підприємства при збільшенні відношення

капіталу до праці на 1 %.

5.

Визначте, на скільки зросте дохід підприємства при збільшенні відношення

K

L

на

0,4.

Задача 1.17. Для даних задачі 1.16 визначте залежність доходу підприємства від

часу, побудувавши трендову регресію

tt

yt



  .

1.

Перевірте значущість коефіцієнта



, 0, 01



 .

2.

Побудуйте надійні інтервали для коефіцієнтів моделі з рівнем надійності 90 %.

3.

Перевірте модель на адекватність із рівнем надійності 99 %.

4.

Визначте, на скільки зростає в середньому дохід підприємства за один період

спостережень.

5.

Зробіть прогноз доходу підприємства на наступний період.

Задача 1.18. Відома інформація про дохід підприємства у млн грн, y , і відношення

його капіталу до працівників





K

L

:

y

K

L

7,

203

6,

242

7,

941

6,

771

7,

314

6,

322

5,

969

5,

337

5,

577

5,

044

6,

048

5,

396

6,

509

5,

737

6,

990

6,

088

5,

808

5,

217

6,

015

5,

372

5,

537

5,

014

7, 6,

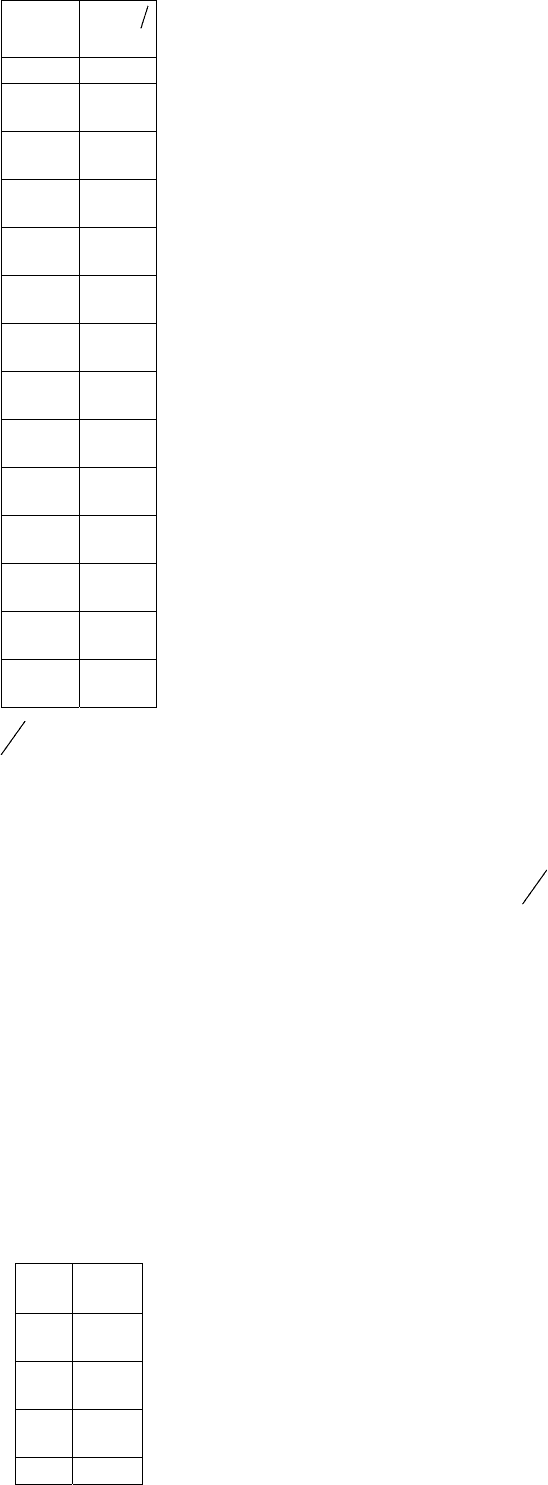
33

y

K

L

663 573

5,

571

5,

039

6,

063

5,

407

7,

427

6,

404

6,

730

5,

899

7,

713

6,

608

6,

804

5,

953

5,

959

5,

330

7,

540

6,

485

6,

330

5,

605

7,

089

6,

160

7,

907

6,

747

5,

831

5,

235

5,

536

5,

013

1. Оцініть функцію Солоу





tt

K

y

L



  .

2.

Побудуйте надійні інтервали для коефіцієнтів моделі з рівнем надійності 90 %.

3.

Перевірте модель на адекватність із рівнем надійності 95 %.

4.

Визначте, на скільки зросте дохід підприємства при збільшенні відношення

капіталу до праці на 2 %.

5.

Визначте, на скільки зросте дохід підприємства при збільшенні відношення

K

L

на

0,1.

Задача 1.19. Для даних задачі 1.18 визначте залежність доходу підприємства від

часу, побудувавши трендову регресію

tt

yt



 

.

1.

Перевірте значущість коефіцієнта



, 0,05



 .

2.

Побудуйте надійні інтервали для коефіцієнтів моделі з рівнем надійності 95 %.

3.

Перевірте модель на адекватність із рівнем надійності 95 %.

4.

Визначте, на скільки зростає в середньому дохід підприємства за один період

спостережень.

5.

Зробіть прогноз доходу підприємства на наступний період.

Задача 1.20. На основі даних про рівень нагромадження (млрд грн),

S

, та дохід

(млрд грн) Y побудуйте регресію вигляду

ttt

SY



  :

S

Y

2

,9

1

5,8

3

,0

1

6,5

3

,1

1

7,2

31

34

S

Y

,3 7,9

3

,4

1

8,6

3

,5

1

9,3

3

,7

2

0,0

3

,8

2

0,7

3

,9

2

1,4

4

,0

2

2,1

4

,2

2

2,8

4

,3

2

3,5

4

,4

2

4,2

4

,6

2

4,9

4

,7

2

5,6

4

,8

2

6,3

4

,9

2

7,0

5

,1

2

7,7

5

,2

2

8,4

5

,3

2

9,1

5

,5

2

9,8

5

,6

3

0,5

5

,7

3

1,2

5

,8

3

1,9

6

,0

3

2,6

6

,1

3

3,3

6

,2

3

4,0

6

,4

3

4,7

6

,5

3

5,4

6

,6

3

6,1

6

,7

3

6,8

1. Визначте значущість коефіцієнтів регресії, 0, 05



 .

2.

Перевірте модель на адекватність із рівнем надійності 95 %.

3.

Побудуйте надійні інтервали для коефіцієнтів моделі з рівнем надійності 95 %.

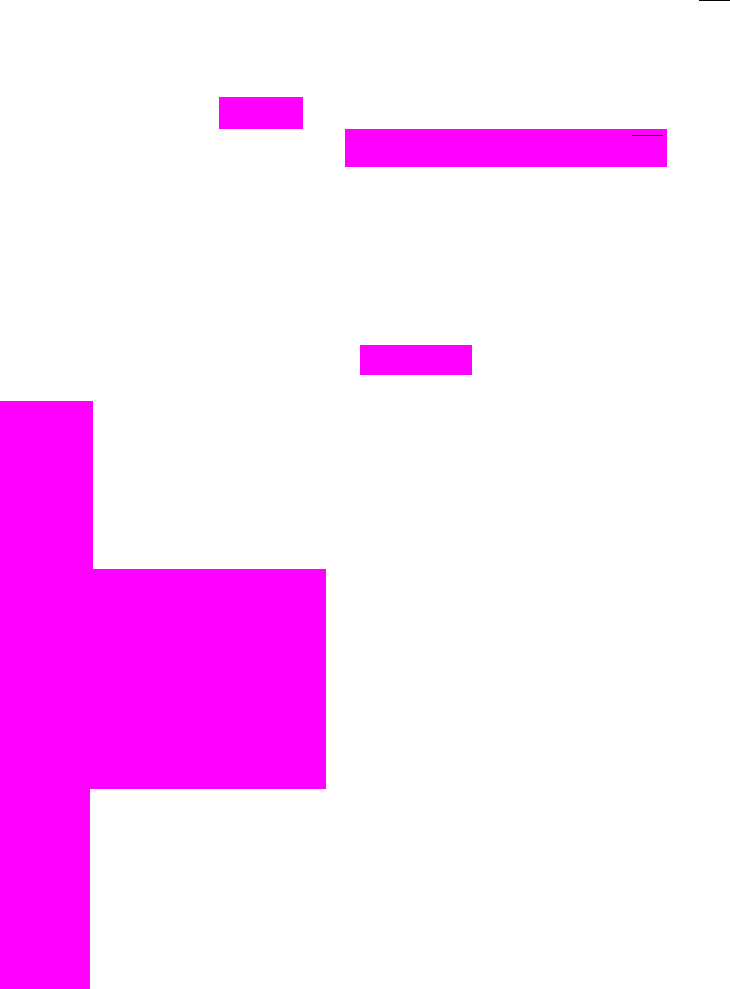
35

4.

Визначте, на скільки відсотків зросте рівень нагромадження, якщо дохід зросте на

5 %.

5.

Обрахуйте коефіцієнт кореляції між змінними, перевірте його значущість, 0,1



 .

Розділ 2. Множинна лінійна регресія

2.1. Описання моделі

За допомогою моделі простої лінійної регресії визначають зв'язок між залежною

змінною y і незалежною змінною x . Модель множинної лінійної регресії описує

співвідношення між

y і набором незалежних змінних

01 1

,,,

k

xx x



 . Наприклад, під час

досліджування треба визначити залежність обсягу попиту на деякий товар від ціни на

цей товар, цін на взаємозамінні з ним товари та від доходів споживачів. У цьому разі слід

застосувати щонайменше три незалежні змінні.

За наявності n спостережень модель множинної лінійної регресії записують у вигляді

0,0 1,1 1,1

,1,,

tt t ktkt

y

xx x tn



      (2.1)

де

tj

x – значення

j

-ї незалежної змінної (

j

x ) у

t

-му періоді. Збурення

t

 задовольняють

тим самим припущенням, що і в моделі простої регресії, де:

 нульове середнє:



M0

t

;

 гомоскедастичність збурень

   

22

DM const, 1,

tt

tn

;



некорельованість збурень cov( , ) 0,

ts

ts   ;



некорельованість збурень і регресорів

,

cov

(

,

)

0, , ,

tsj

xts

j



 (якщо регресори

нестохастичні, то це припущення виконано автоматично);



збурення

t

 нормально розподілені для всіх t.

Модель множинної лінійної регресії (2.1) зручно записувати в матрично-векторному

вигляді



y

X

βε (2.2)

з використанням таких позначень:

1

2

.

n

y











y – вектор значень залежної змінної;

10 11 1, 1

20 21 2, 1

01 ,1

k

nn nk

xx x













   





   



   







X

– матриця значень незалежних змінних;



























1

2

n

ε  – вектор збурень;

36































0

1

1k

β – вектор параметрів (коефіцієнтів) регресії.

Матриця

X складається з n рядків – відповідно до кількості спостережень, і з

k

стовпчиків, кількість яких дорівнює кількості незалежних змінних. Щоб записати модель

із константою

01,1 1,1

,1,

ttktkt

y

xxtn



     

у матричному вигляді, розглядають матрицю значень незалежних змінних, у якій перший

стовпчик складається з одиниць

11 1, 1

21 2, 1

1,1

1

k

nnk

xx















 







 





 







X

.

Позначимо через

Dε

коваріаційну матрицю вектора збурень. Тоді внаслідок того,

що збурення мають нульові математичні сподівання, маємо:













    













    



11213 1

21 2 23 2

12

D cov( , ) cov( , ) cov ,

cov( , ) D cov( , ) cov ,

D

cov( , ) cov( , ) D

n

nn n

ε







     





 



 



      



2

11213 1

2

21 2 2 3 2

2

123

MM M M

MMM M

M

()

MM M M

n

T

nn n n

εε

,

Припущення 2 та 3 щодо збурень регресії зручно записувати у вигляді





2

Dε I

,

де I – одинична матриця n -го порядку, а припущення 1 у вигляді M0ε .

Таким чином, модель множинної лінійної регресії в матрично-векторних позначеннях

має такий вигляд:









2

,

M0,

D,

yXβε

ε

ε I

ε

не залежить від X; 

2

~(0, )Nε I .

2.2. Знаходження параметрів регресії методом найменших квадратів

Нехай



  

01 1

ˆ

ˆˆ ˆ

( , ,..., )

T

k

β – деяка оцінка вектора параметрів β . Запишемо рівняння

вибіркової регресії

00 11 1 1

ˆˆ ˆ

ˆ

,

kk

yx x x



    .

Тоді

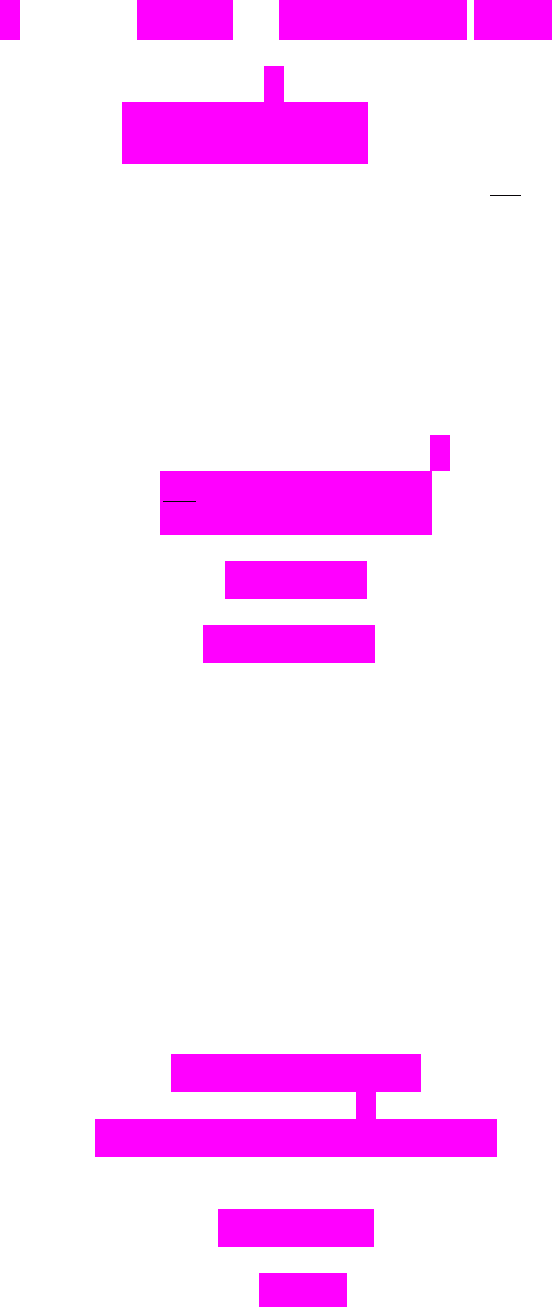
37

00 1 ,1 1 , 1

ˆˆ ˆ

ˆ

ttktk

yxx x



   

є оцінкою математичного сподівання

t

My

, побудованою на основі вибіркової регресії.

Залишки

ˆ

t

 визначаємо як різниці між значеннями y , які спостерігались, і обчисленими

з регресії:

ˆ

ttt

yy  .

Вектор залишків

ˆ

ε дорівнює



ˆ

ε yy

, де 

12

ˆˆˆ ˆ

(

,,,

)

T

n

yy yy , 

ˆ

yXβ .

Оцінки методу найменших квадратів знаходять з умови мінімізації суми квадратів

залишків за всіма можливими значеннями

ˆ

β :







2

1

ˆ

ˆˆ

ˆ

() ( ,)

n

T

t

QQβεε

(2.3)

Якщо регресію записати у вигляді

0,0 1,1 1,1

,1,

tt t ktkt

y

xx x tn



     

,

то оцінки МНК можна знайти, розв'язавши систему нормальних рівнянь:

0 1 1, 2 2, 1 1,

2

0 1, 1 1, 2 1, 2, 1 1, 1, 1,

2

0 1, 1 1 1, 2 2 1, 1 1, 1,

,

.

ttkktt

tt ttktkttt

kt kt kt k kt ktt

nxx xy

x x xx xx xy

xxx xx xx

y



 

    





  







   



 

  

  







(2.4)

Щоб мінімізувати вираз (2.3) у векторному вигляді, запишемо необхідну умову

екстремуму, тобто прирівняємо часткові похідні відносно

ˆ

β до нуля. Маємо





 



ˆ

22 0

ˆ

TT

Q

Xy XXβ

β

,

тобто система нормальних рівнянь (2.4) у матричній формі набуває вигляду



ˆ

T T

XXβ Xy

,

звідки





1

ˆ

()

TT

β XX Xy. (2.5)

Перевірка достатніх умов екстремуму показує, що

ˆ



, обчислена за (2.5), насправді

мінімізує функцію (2.3). Таким чином, оцінку методу найменших квадратів коефіцієнтів

моделі множинної лінійної регресії можна знайти за формулою (2.5).

Рівняння вибіркової регресії набуває вигляду

00 11 1 1

ˆˆ ˆ

ˆ

kk

yx x x



    ,

або, у випадку регресії з константою

011 11

ˆˆ ˆ

ˆ

kk

yx x



    .

Рівняння вибіркової регресії є рівнянням лінійної функції багатьох змінних.

2.3. Властивості залишків методу найменших квадратів

Для прикладу розглянемо множинну регресію вигляду

011, 11,

ˆˆ ˆ

ˆ

ttkkt

yx x



   

.

Використовуючи введені вище векторно-матричні позначення, можна записати





1

ˆ

()

TT

yXβ XX X X y.

Вектор залишків методу найменших квадратів

ˆ

ε визначаємо як



 

T1T

ˆ

(() )

ε yy yXβ IXXX Xy.

Зміст поняття залишків такий самий, як і в моделі простої лінійної регресії. Запишемо

систему нормальних рівнянь у такому вигляді:

T

()0



XX y



,

або



T

ˆ

0

X ε

(2.6)

38

Очевидно, що вектор залишків ортогональний до кожного стовпчика матриці X.

Згадаємо, що

j

-й стовпчик цієї матриці утворюють значення

j

-го регресора. Таким

чином,

залишки методу найменших квадратів ортогональні до регресорів. Якщо

розглядати модель із константою, то перший стовпчик матриці

X складається з одиниць, і

з рівняння (2.6) випливає, що

1

ˆ

0

n

t

t 







(2.7)

З останньої рівності випливає, що в моделі з константою сума залишків методу

найменших квадратів дорівнює нулю

.

Оскільки 

ˆ

yXβ , то

  

ˆˆ

ˆˆ ˆ ˆ

ˆˆ

(,) ( ) 0

TTTT

y ε y ε Xβε βX ε (2.8)

унаслідок (2.7). Крім того, вектор

ˆ

y є лінійною комбінацією стовпчиків матриці X , тобто

регресорів.

Зі співвідношення (2.8) випливає важливий наслідок: регресійна гіперплощина в моделі

з константою проходить через точку, координати якої дорівнюють середнім значенням

незалежних змінних.

2.4. Статистичні властивості оцінок методу найменших квадратів. Теорема

Гауса – Маркова

Покажемо, що МНК-оцінка є незміщеною оцінкою β :

 



 

 













11 1

11

ˆ

MM M M

M.

TT TT TT

TT TT

β XX Xy XX X y XX X Xβε

XX XXβ XX X εβ

Знайдемо коваріаційну матрицю МНК-оцінки:



 



   



 

 



 

 

 

 



  







11 1

11 11

22

1

2

ˆ

.

T

TT TT TT

T

TT TT TTT

T

DD D

I

β XX Xy XX X y XX X

XX X XX X XX XXXX

XX

Таким чином,

ˆ

M,







2T-1

ˆ

D().β XX (2.9)

Безпосередньо дисперсії кожного з коефіцієнтів регресії містяться на головній діагоналі

отриманої матриці. Проте наведені формули не можна використовувати для перевірки

гіпотез та інтервального оцінювання, оскільки до них входить невідомий параметр –

дисперсія збурень

2

 . Можна показати, що статистика

2

ˆ

RSS

nk





, (2.10)

де

k

– кількість регресорів, включаючи константу, є незміщеною оцінкою

2



. Якщо

збурення нормально розподілені, то

ˆ



має багатовимірний нормальний розподіл,

математичне сподівання і дисперсію якого обчислюємо за формулою (2.9).

Величина

2

1

22

ˆ

()

n

t

nk

RSS













має 

2

– розподіл з nk степенями свободи і не залежить від

ˆ



. Оцінку коваріаційної

матриці коефіцієнтів регресії за методом найменших квадратів одержуємо, підставивши

до формули (9) виразу (10) замість дисперсії збурень

2



:

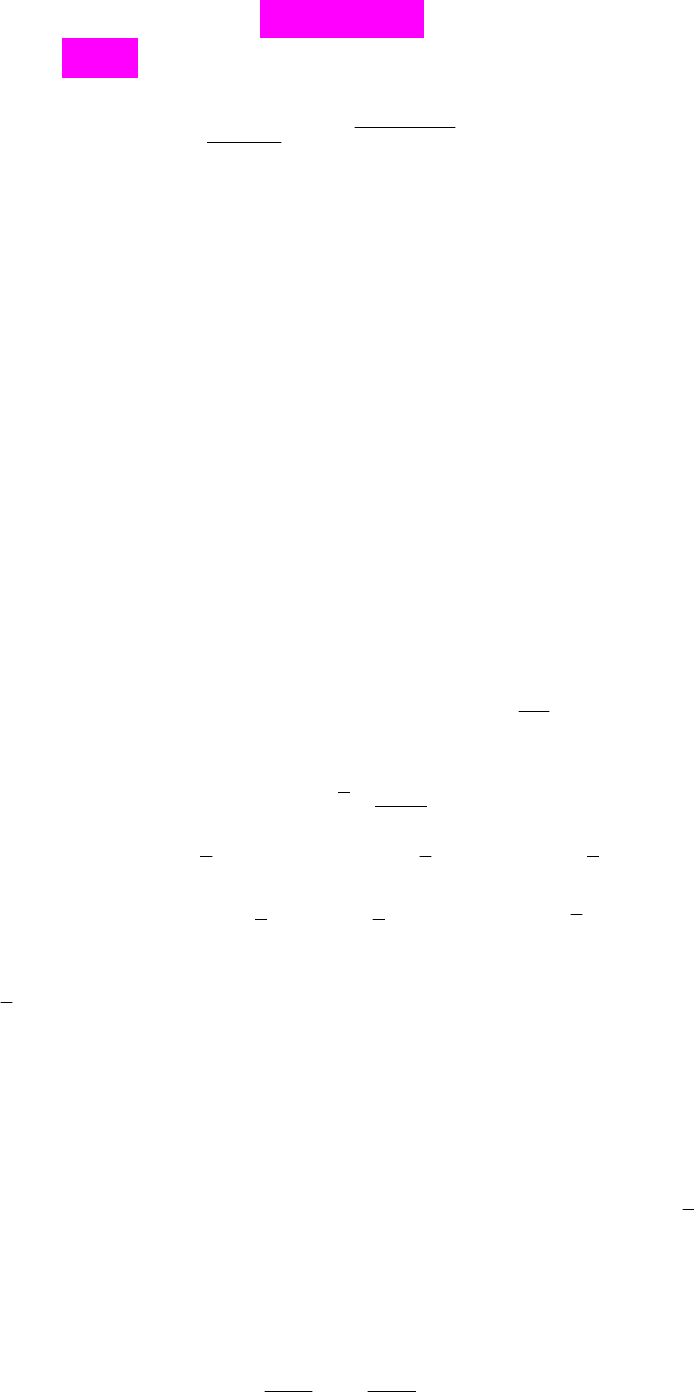
39



2-1

ˆ

Dˆ( )

T

β XX .

Позначимо через 

ˆ

s.e.

()

j

оцінку середньоквадратичного відхилення коефіцієнта

ˆ

j



.

Розмірковуючи таким чином, як у випадку простої регресії, доходимо висновку, що

ˆ

~,0,1.

ˆ

s.e.( )

jj

nk

j

tjk











(2.11)

Оцінки методу найменших квадратів є лінійними в тому розумінні, що

ˆ

 – лінійна

функція

y

. Наведена теорема визначає оптимальні властивості оцінки методу

найменших квадратів.

Теорема Гауса – Маркова:

1. Нехай припущення про нормальність збурень не накладено. Тоді МНК-оцінки будь-

якої лінійної комбінації параметрів регресії мають найменшу дисперсію в класі

незміщених лінійних оцінок.

2. Припустимо, що збурення мають нормальний розподіл. Тоді МНК-оцінки будь-якої

лінійної комбінації

параметрів регресії мають найменшу дисперсію в класі незміщених

оцінок.

Таким чином, оцінки коефіцієнтів

ˆ



мають найменші дисперсії серед оцінок

відповідних класів.

2.5. Розклад дисперсії залежної змінної. Коефіцієнт детермінації.

Скоригований коефіцієнт детермінації

Як і в моделі простої лінійної регресії, суму квадратів відхилень залежної змінної можна

розкласти на дві частини. Проте такий розклад суттєво залежить від того, чи є в регресії

константа.

Нехай константа існує в регресії, тобто ми розглядаємо модель вигляду

01,1 1,1

,1,

ttktkt

y

xxtn



      .

Тоді внаслідок (2.6)-(2.8), а також того, що

1

ˆ

n

t

y

n





маємо

222

11 1

2222

11 1 11

ˆˆ ˆ

ˆ

() ( )( )

ˆˆ ˆˆ

ˆˆ ˆ

2

()() ()

.

nn n

t ttt tt

tt t

nn n nn

ttt t tt

tt t tt

TSS y y y y y y y y

yy yy yy

 

  



 

     

 

  

Як і раніше,

2

1

ˆˆ

()

n

t

ESS

yy







– пояснена сума квадратів,

2

1

ˆ

n

t

RSS







– сума квадратів залишків.

Отже, формулу

розкладу дисперсії слід використовувати й у випадку множинної

регресії

.

TSS ESS RSS



 (2.12)

Якщо ж константи немає в регресії, то подвійний добуток

1

ˆ

2

()

n

tt

t

yy







не завжди

дорівнюватиме нулю, а тому не можна стверджувати, що завжди виконуватиметься

тотожність (2.12).

Коефіцієнт множинної детермінації (або коефіцієнт детермінації

2

R

треба

визначати як частку поясненої і загальної сум квадратів:

2

1

ESS RSS

R

TSS TSS

 (2.13)

Коефіцієнт множинної детермінації показує, яку частину дисперсії залежної змінної

пояснюють за рахунок моделі, або, іншими словами, незалежними змінними в сукупності.

40

Підкреслимо, що коефіцієнт детермінації є мірою щільності саме лінійного зв'язку між

залежною та незалежними змінними.

Коефіцієнт детермінації завжди перебуває в межах від нуля до одиниці. Що ближче

2

R

до 1, то тісніший зв'язок між змінними. Якщо

2

1R



, то це означає, що всі значення y

належать гіперплощині, породженій стовпчиками матриці X . Якщо

2

0R  , то лінійного

зв'язку між змінними немає. Коефіцієнт детермінації використовують як міру згоди і для

множинної регресії.

Також слід зазначити, що в моделях без константи через порушення тотожності (2.12)

різні способи визначення

2

R дають різні результати, і коефіцієнт детермінації важко

інтерпретувати. Тому в жодному разі не можна співвідносити моделі з константою і без

константи на підставі порівняння коефіцієнтів детермінації. Якщо немає економічних

підстав обрати регресійну функцію у вигляді без константи, то бажано розглядати модель

з константою.

Одним із суттєвих недоліків коефіцієнта детермінації є

те, що при додаванні регресорів

2

R

зростає. Також під час найпростіших перетворень залежної змінної коефіцієнт

детермінації суттєво змінюється. Тому для порівняння моделей з різною кількістю

регресорів, а також моделей з різною функціональною формою змінних використовують

скоригований коефіцієнт детермінації

2

1

adj

ESS

nk

R

TSS

n







.

Очевидно, що при цьому значення скоригованого коефіцієнта детермінації можна

виразити через величину

2

R





22

1

11

adj

n

RR

nk



 



.

Неважко показати, що для будь-яких 1

k  коефіцієнт детермінації більший за

скоригований коефіцієнт детермінації:

22

adj

RR .

Це означає, що скоригований коефіцієнт детермінації занижує якість побудованої

моделі залежно від кількості додаткових регресорів, що дозволяє більш коректно

порівнювати моделі з різною кількістю чинників.

Нарешті, з огляду на останню нерівність, скоригований коефіцієнт детермінації не

може перевищувати 1. Чим ближче до 1 його значення, тим ліпше побудована модель.

На відміну від звичайного

коефіцієнта детермінації, величина скоригованого

коефіцієнта детермінації може бути від'ємною.

Приклад 2.1. Оцінювання множинної регресії

Бюджетне обстеження п'яти випадково вибраних сімей дало такі результати:

Сім'я

1

2

3

4

5

Нагромадження,

S

3

6

5

3

,5

1

,5

Дохід, Y

4

0

5

4

5

3

0

3

0

Майно, W

6

0

3

6

3

6

1

5

9

0

Оцініть регресію S на Y та W з константою. Спрогнозуйте нагромадження сім'ї, якщо

її дохід 40 тис. грн, а майно 25 тис. грн. Нехай дохід зріс на 10 тис. грн. Як зростуть

нагромадження сім'ї? Знайдіть коефіцієнт детермінації моделі.

Розв'язання

Оцінимо регресію

01 2

,1,5

tttt

SYWt    

. Для знаходження коефіцієнтів регресії

можна скористатися двома способами.

Черняк О.І. та ін. Економетрика

Подождите немного. Документ загружается.