Черняк О.І. та ін. Економетрика
Подождите немного. Документ загружается.

343
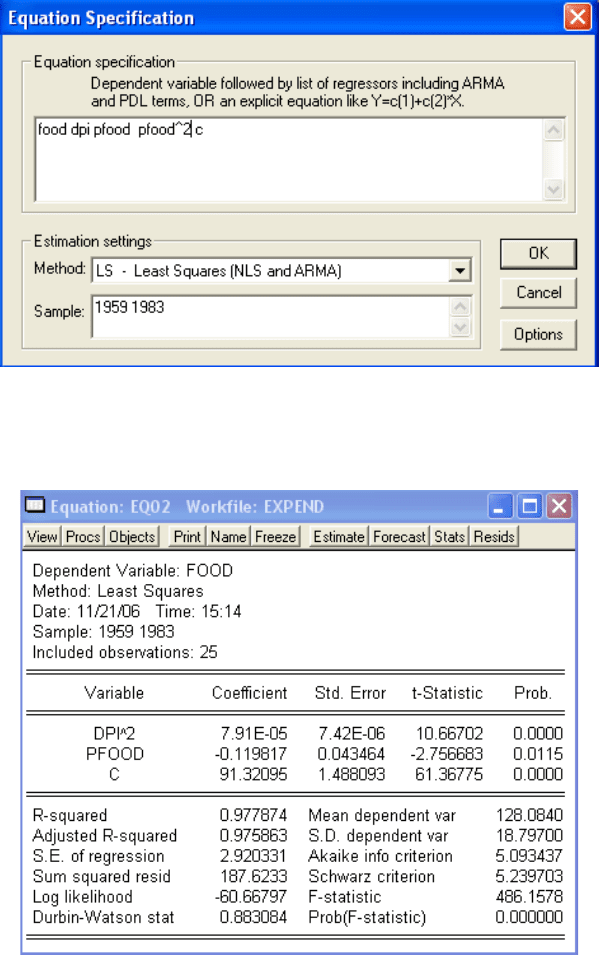
Рис.13.19. Специфікація для другої моделі
Отримаємо такі результати оцінювання першої та другої моделей:

344
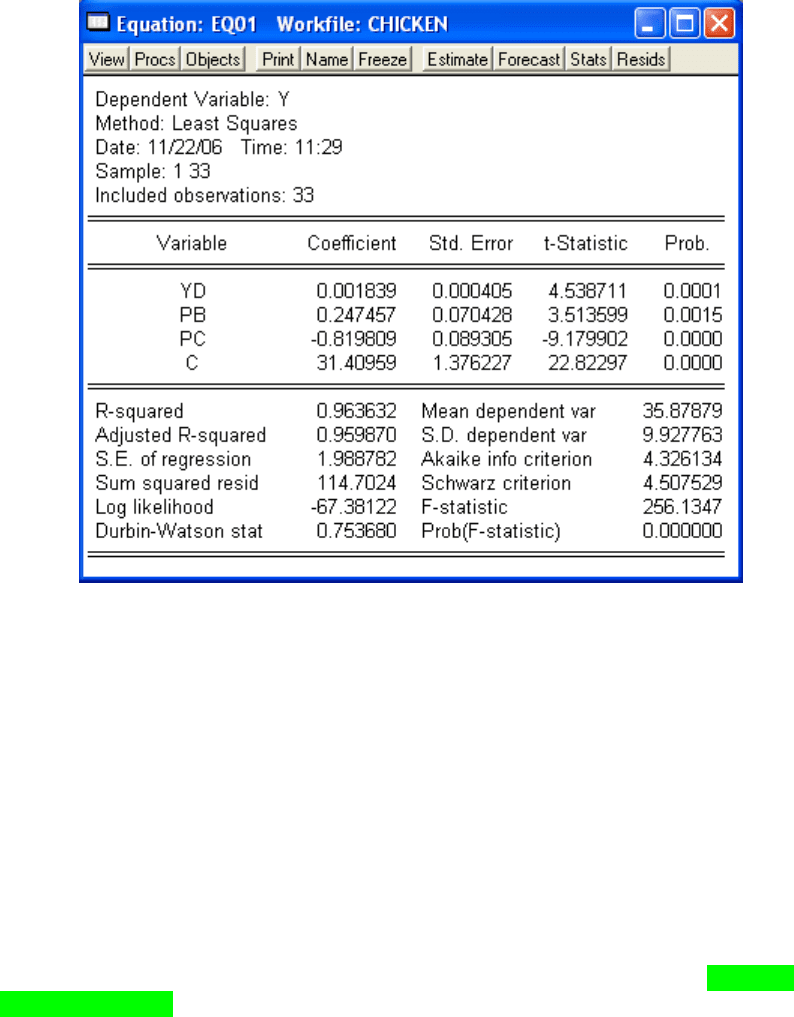
Рис.13.20. Результати оцінювання першої та другої моделей
Таким чином, найкращі результати в цьому випадку
продемонстрували нелінійні моделі.
13.4. Перевірка статистичних гіпотез
У цьому розділі буде розглянуто перевірку таких гіпотез:
1. Про адекватність моделі.
2. Про значення коефіцієнта моделі.
3. Про значущість коефіцієнта моделі.
4. Про стійкість моделі.
5. Про лінійні обмеження на коефіцієнти моделі.
Спочатку побудуємо таке регресійне рівняння:
345
Рис.13.21. Приклад побудування регресійного рівняння
13.4.1. Гіпотеза про адекватність моделі
Для перевірки моделі на адекватність слід порівняти практично
знайдене значення F-статистики з теоретичним значенням.
Адекватність моделі означає, що ми відхиляємо гіпотезу про те, що всі
коефіцієнти моделі одночасно дорівнюють 0. У цьому випадку,
практичне значення F-статистики дорівнює 256,1347. Теоретичне
значення можна знайти з таблиці розподілу Фішера з 3 та 29
степенями свободи та
заданим рівнем значущості = 0,05 (2,93).
Оскільки практичне значення більше ніж знайдене теоретичне
значення статистики Фішера, можна зробити висновок про
адекватність побудованої моделі.
Те саме можна зробити іншим способом, оскільки Prob. (F-
statistic) = 0,0000, що менше ніж 0,05 (рівень значущості), тому можна
зробити висновок про адекватність моделі за рівня значущості 0,95.
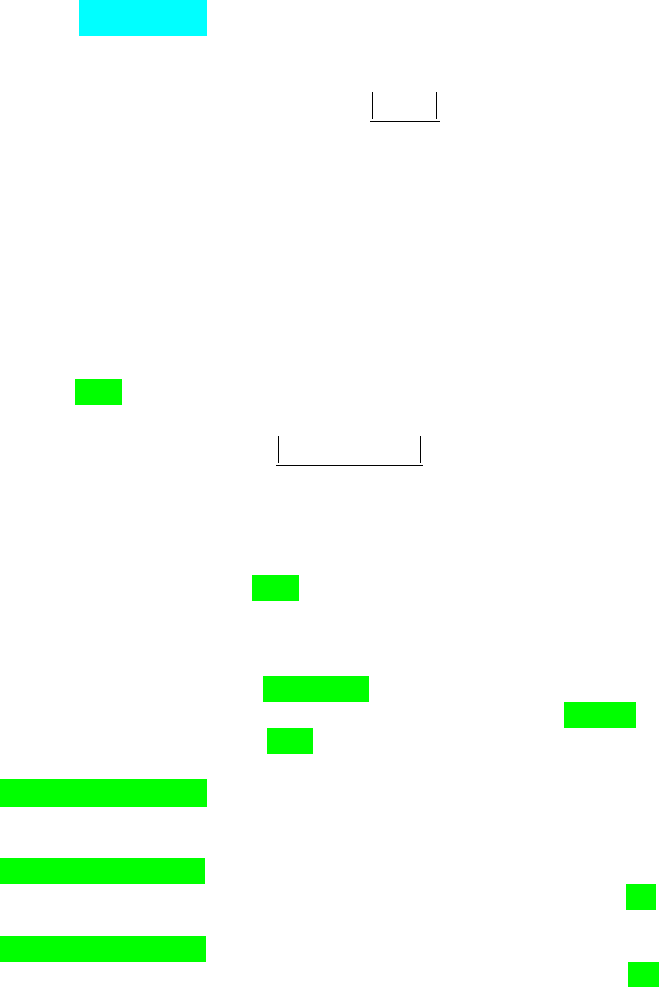
346
13.4.2. Гіпотеза про значення коефіцієнта моделі
Для перевірки гіпотези про значення m оцінки коефіцієнта
i
b моделі
o
(:β )
i
Hm слід порівняти практично знайдене значення t-
статистики розподілу Стьюдента з теоретичним значенням.
Практичне значення підраховуємо за формулою
,
..
()
i
pr
i
m
t
se
де
i
– коефіцієнт, значення якого перевіряють; i – номер коефіцієнта
i = 0,1,...; m – значення для перевірки;
..( )
i
se
– стандартне
відхилення для цього коефіцієнта.
Далі за вибраним рівнем значущості або рівнем надійності
1 у
таблиці розподілу Стьюдента з n - k степенями свободи знаходимо
критичне значення t
кр
. Якщо t
pr
< t
кр
, то гіпотезу H
0
можна прийняти.
Якщо t
pr
t
кр
, то гіпотезу H
0
слід відхилити.
Наприклад, перевіримо гіпотезу про значення коефіцієнта при
змінній РВ 2 за рівнем надійності 0,95. Для цього розрахуємо
практичне значення t-статистики:
0,247457 2
23,5937.
0,070428
pr
t
Теоретичне значення
t-статистики дорівнює 2,045. Оскільки
практичне значення t-статистики перевищує теоретичне, можна
зробити висновок про відхилення нульової гіпотези про рівність
коефіцієнта при змінній РВ 2.
13.4.3. Гіпотеза про значущість коефіцієнта моделі
У програмному пакеті Eviews 4.0 для перевірки значущості змінної
(рівності змінної нулеві) слід порівняти значення p-value (у таблиці
результатів – це стовпчик Prob) з рівнем значущості.
Наприклад, для цієї моделі:
Prob. (YD) = 0,0001, що менше ніж 0,01 та 0,05 (рівень значущості),
тому можна зробити висновок про значущість змінної
YD за будь-
якого рівня значущості.
Prob. (PB) = 0,0015, що менше ніж 0,01 та 0,05 (рівень значущості),
тому можна зробити висновок про значущість змінної PB за рівня
значущості 0,05 та 0,01.
Prob. (PC) = 0,0000, що менше ніж 0,01 та 0,05 (рівень значущості),
тому можна зробити висновок про значущість змінної PC за будь-
якого рівня значущості.
347
13.4.4. Гіпотеза про лінійні обмеження на коефіцієнти
моделі
Нехай ми маємо перевірити такі гіпотези:
4)3()1(
cc та 1)2(
c
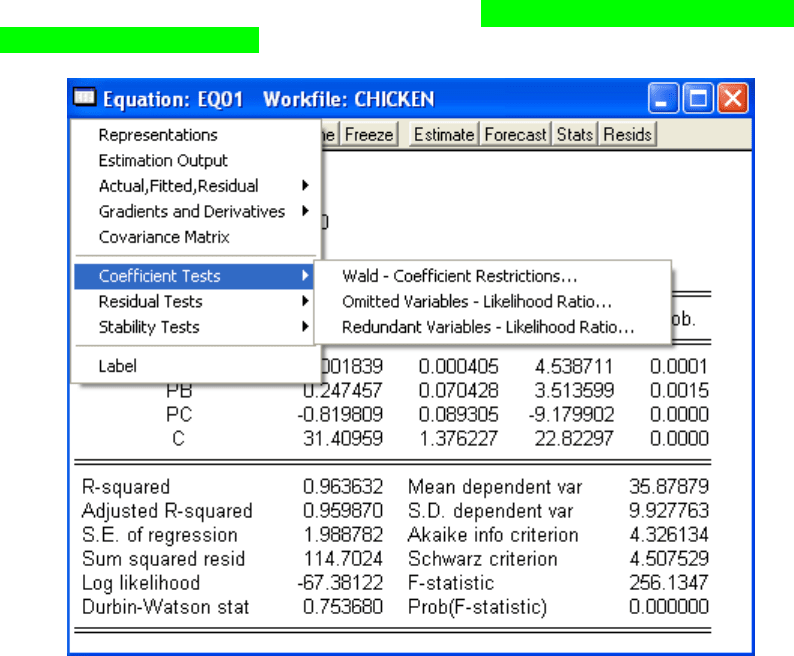
Для цього треба (перебуваючи у вікні результатів оцінювання
моделі) обрати в меню такі команди: ViewCoefficient TestsWald-
Coefficient Restrictions… :
Рис.13.22. Перевірка гіпотез
У діалоговому вікні вказують вид гіпотези:
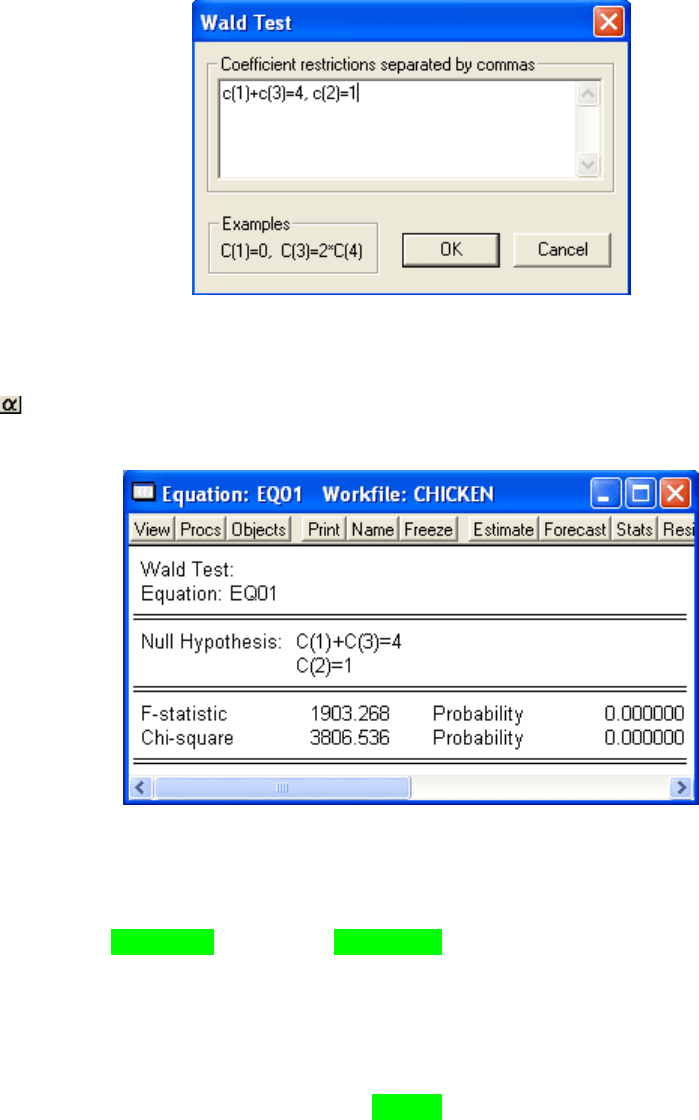
348
Рис.13.23. Вид гіпотези
Для уточнення індекси коефіцієнтів можна переглянути в об’єкті
с.
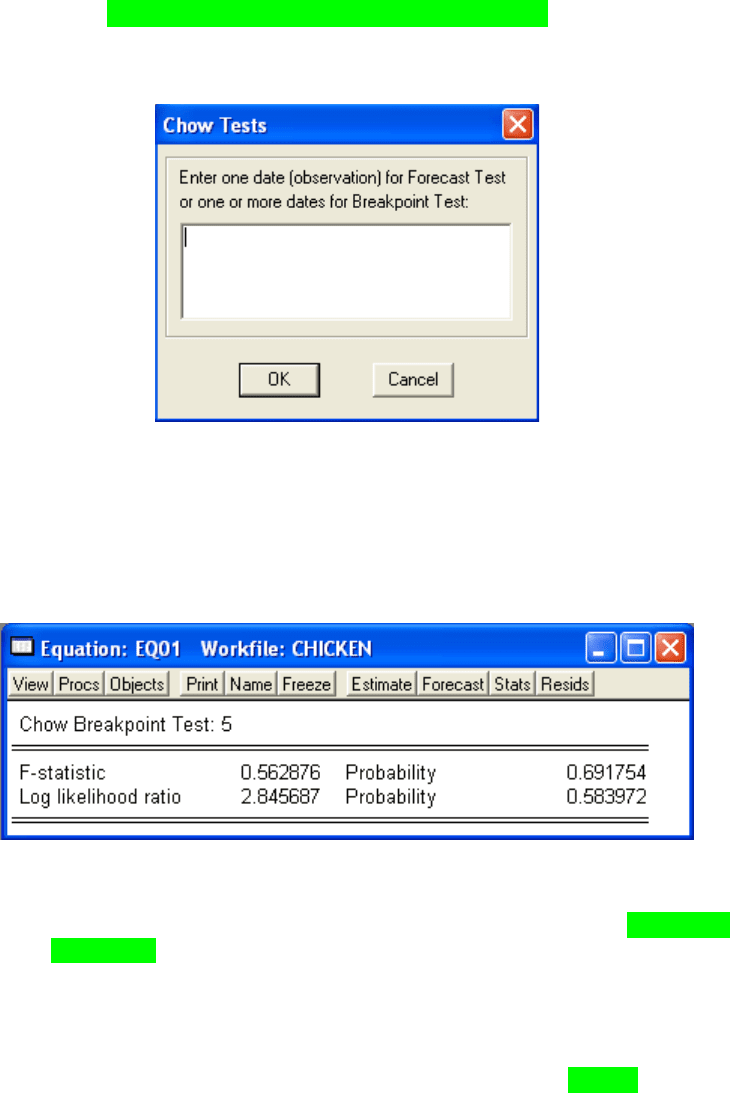
Вікно результатів матиме такий вигляд:
Рис.13.24. Вікно результатів перевірки гіпотези
Нехай рівень значущості дорівнює 0,05. Результати перевірки
свідчать про те, що нульову гіпотезу слід відхилити, оскільки
значення Probability навпроти Chi-square менше ніж 0,05.
Нагадаємо, що значенням F-статистики можна користуватися
лише за припущення про нормальний розподіл збурень регресії, в
іншому випадку слід використовувати значення
2
.
13.4.5. Перевірка гіпотези про стійкість моделі
У програмному середовищі Eviews для перевірки гіпотези про
стійкість моделі за допомогою критерію переломної точки Чоу треба
349
(перебуваючи у вікні результатів оцінювання моделі) обрати в меню
такі команди: ViewStability TestsChow Breakpoint test та ввести дату
або номер спостереження, під час якого відбулися певні зміни
(переломні точки):
Рис.13.25. Вікно введення дати або номеру спостереження
Припустимо, що треба перевірити гіпотезу про структурні
зрушення в п'ятому спостереженні. Для цього введемо у вікно цифру
5, що позначає п'яте спостереження.
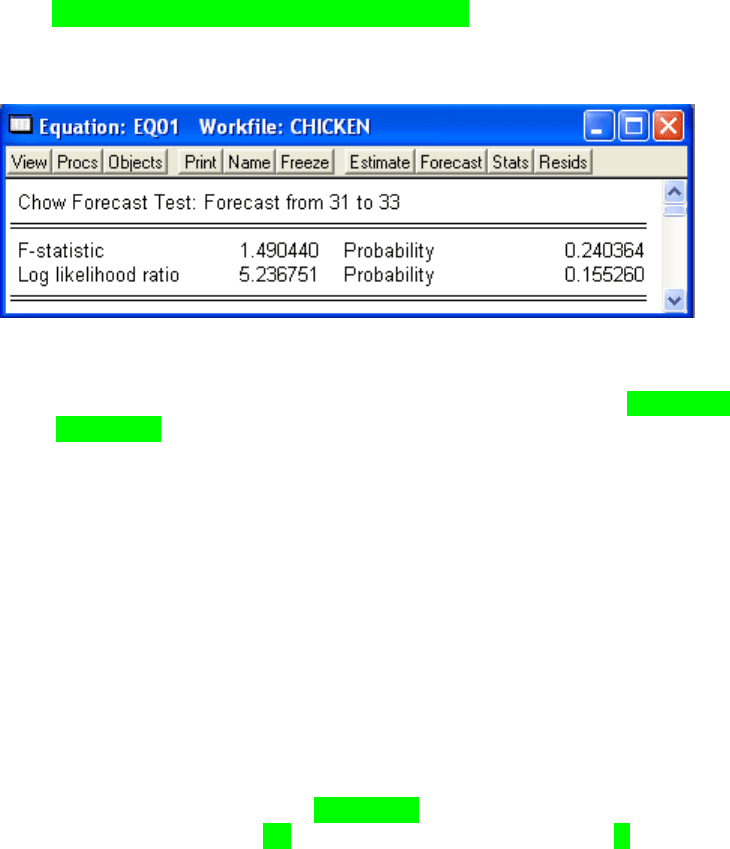
Вікно результатів матиме такий вигляд:
Рис.13.26. Вікно результатів перевірки гіпотези про стійкість моделі -1
Нехай рівень значущості дорівнює 0,05. Оскільки Probability
навпроти F-statistics більше ніж 0,05, тоді приймаємо нульову гіпотезу
про відсутність структурних змін, що відбулися в п’ятому
спостереженні.
Прогностичний критерій Чоу
застосовують у випадках, коли одна з
двох груп має невелику кількість спостережень, недостатню для того,
щоб знайти оцінки. Щоб зробити цей тест в Eviews, треба
(перебуваючи у вікні результатів оцінювання моделі) обрати в меню
350
команди ViewStability TestsChow Forecast test та ввести дату або
номер спостереження, під час якого відбулися певні зміни (переломні
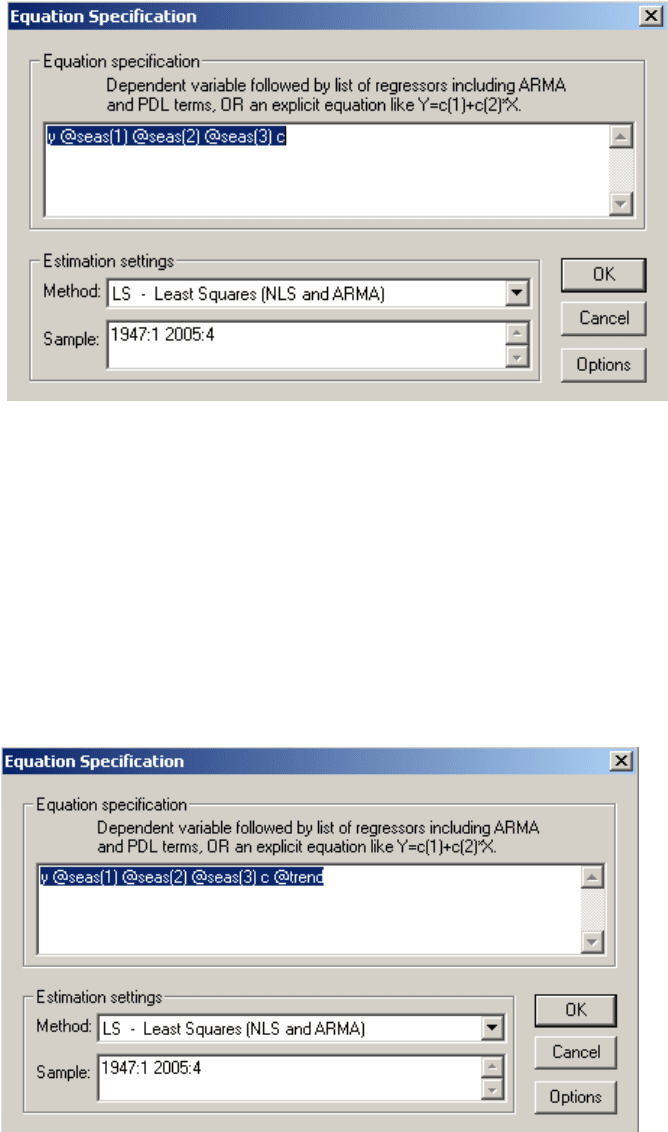
точки) – у цьому випадку 31:
Рис.13.27. Вікно результатів перевірки гіпотези про стійкість моделі -2
Нехай рівень значущості дорівнює 0,05. Оскільки Probability
навпроти F-statistics більше ніж 0,05, то можемо прийняти нульову
гіпотезу про відсутність структурних змін, що відбулися в 31-ому
спостереженні.
13.5. Види лінійної регресії
У цьому підрозділі розглянемо різновиди регресійних моделей, а
саме: включення сезонних коливань та лінійного тренду до моделі та
моделювання за допомогою функції Кобба – Дугласа.
13.5.1. Визначення сезонних коливань
Нехай треба проаналізувати часовий ряд
t
y
на наявність сезонних
коливань.
Одним із поширених способів моделювання сезонності є
використання фіктивних змінних. Для побудування регресійної
моделі слід застосувати функцію @seas(N). Як і всі функції системи, її
запис починається зі знака @. Ця функція має параметр N – номер
сезону в році. Наприклад, для оцінювання регресії вигляду
11 2 2 3 3to t
yqqq
у вікні специфікації регресії слід указати:
351
Рис.13.28. Використання фіктивних змінних
У цьому випадку в моделі використано три фіктивні змінні,
оскільки періодичність даних була квартальною.
У випадку місячної структури даних слід було б використати 11
фіктивних змінних.
Розглянемо такі моделі:
11 2 2 3 3to t
yqqq
11 2 2 3 3 4to t
yqqqt
Для першої моделі специфікація моделі аналогічна попередній.
Для другої моделі у вікні специфікації запишемо:
352
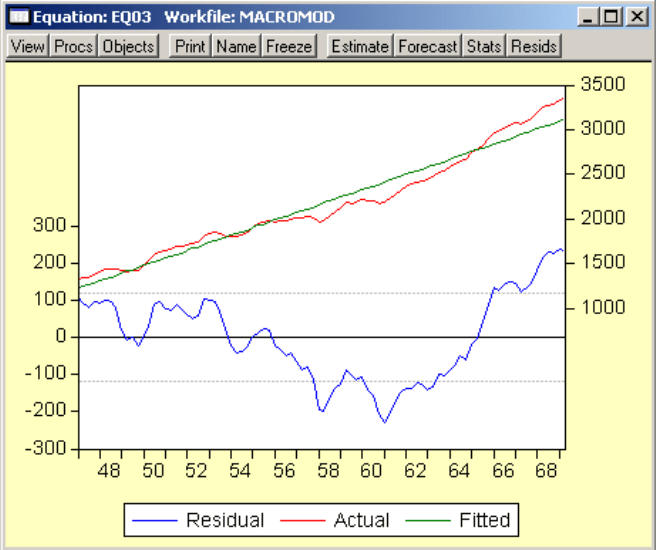
Рис.13.29. Використання фіктивних змінних для другої моделі
Для ілюстрації побудуємо графік оціненої регресії:
Рис.13.30. Графік оціненої регресії
13.5.2. Функція Кобба – Дугласа
2
1
0
,YKL
де
Y
– індекс реального обсягу виробництва;
K
– індекс реальних
капітальних витрат;
L
– індекс реальних витрат праці.
Для того щоб звести модель до лінійної регресії, слід логарифмувати
задану функцію. Для цього у вікні специфікації записуємо:
