Черняк О.І. та ін. Економетрика
Подождите немного. Документ загружается.

247
агрегованому ринку праці в умовах недосконалої конкуренції. Зауважимо, що моделі
попиту та пропозиції є моделями часткової рівноваги, тоді як решта є моделями загальної
рівноваги, де два співвідношення, скажімо, AD (сукупний попит) та AS (сукупна
пропозиція) передбачають рівновагу на кількох ринках (агреговані ринки товарів,
робочої сили та фінансовий ринок). Однак усі ці
моделі мають подібну геометричну
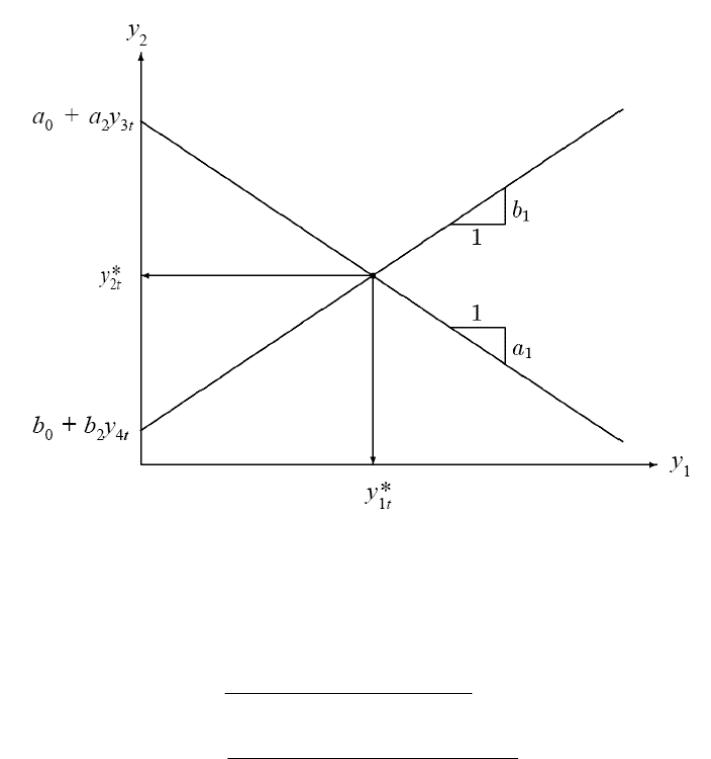
інтерпретацію (див. рис. 10.1)
Нехай у
1
та y
2
– ендогенні змінні, а у
3
та y
4
– екзогенні змінні. Припустимо, що
змінні пов'язані через такі два структурні відношення для ендогенних змінних:
201123
201124
,
.
d
ttt
s
ttt
y
aa
y
a
y
ybbyby
(10.25)
Усі параметри для зручності вважають додатними (негативний ефект передають за
допомогою знаку "мінус"). Ці відношення зазвичай інтерпретують як поведінкові
відношення, що описують наміри економічних агентів. Верхні індекси d та s указують на
те, що ми маємо справу з намірами стосовно попиту та пропозиції (це не обов'язково,
оскільки метою є
надати більшу конкретність нашому аналізові).
Модель є лінійною. Тому для більшої реалістичності будемо розглядати логарифми
вихідних економічних змінних. Лог-лінійсть можна інтерпретувати як локальну
апроксимацію справжньої залежності.
Модель проілюстровано на рис. 10.1
Рис. 10.1. Теоретична модель для фіксованих значень екзогенних змінних
За умови
11
ba (криві на рис. 10.1 не паралельні) у моделі існує і єдина точка
рівноваги
22
ds
tt
yy
:
023 024
1
11
10 23 10 24
2
11
()()
*,
()()
*.
tt
t
tt
t
aay bby
y
ab
ba ay ab by
y
ab
(10.26)
Зазначимо, що в цьому підрозділі ми вживатимемо термін "рівновага" у тому розумінні,
що наміри реалізовані.
Ґрунтуючись на структурних відношеннях і припущенні про існування рівноваги,
економісти починають аналізувати рівноважні ефекти на ендогенні змінні, спричинені
зміною екзогенних. Ці ефекти виражаються як часткові похідні рівноважних значень
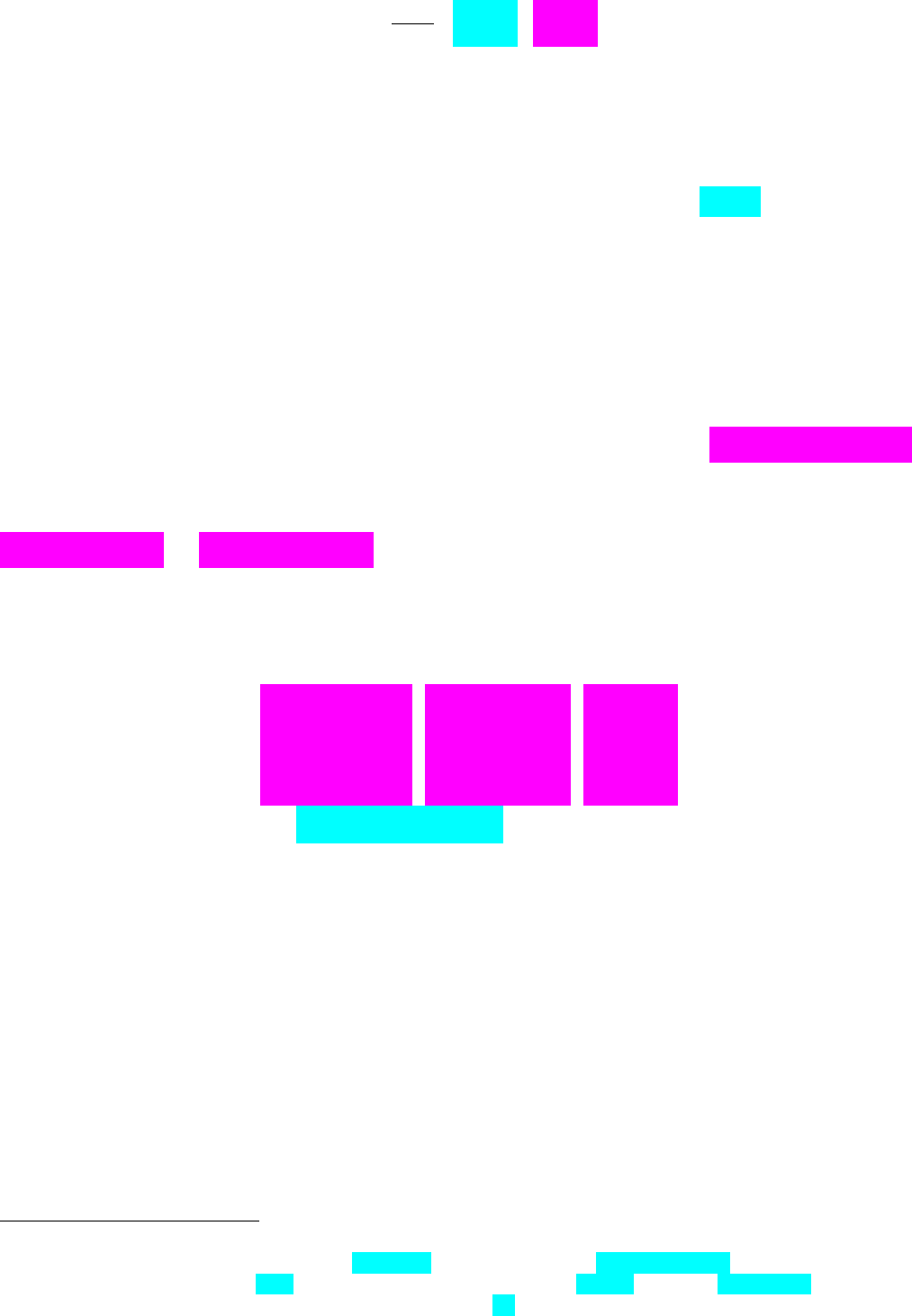
248
(10.26) стосовно екзогенних змінних,
,
,
*
tk
tl
y
y
, =1,2k ,
3,4l . Вони називаються ефектами
порівняльної статики.
Розглянемо більш конкретну ситуацію, яка вкладається в нашу схему. Нехай наша мета
– проаналізувати попит і пропозицію на ринку курятини. Перше з рівнянь (10.25) є
(оберненою) функцією попиту, а друге – (оберненою) функцією пропозиції. Дві ендогенні
змінні у
1
та y
2
– це кількість та ціна курятини; екзогенні змінні: у
3
– ціна м'яса, y
4
–
ціна на вхідні ресурси виробництва. Отже, зростання y
4
зміщує криву пропозиції
вгору, оскільки збільшує виробничі витрати. Припущення
2
>0a означає, що
курятина та м'ясо є взаємозамінними товарами (ефект заміщення переважає). Таким
чином, ми розглядаємо часткову рівновагу на ринку курятини. Наша мета полягає в
тому, щоб провести відповідність між основними поняттями теоретичної моделі,
проілюстрованої на рис. 10.1, такими, як припущення про існування рівноваги,
структурні відношення, розділення змінних на ендогенні/екзогенні,
порівняльна
статика та концепціями VEC-моделі (або коінтегрованої векторної авторегресії,
СVAR
18
): коінтеграційними відношеннями, спільними трендами, множиною
атракторів, функцією імпульсної реакції, довгостроковими ефектами.
VEC-модель часткової рівноваги на ринку курятини. Зрозуміло, що наша
теоретична модель передбачає VEC-модель із чотирма змінними
T
123 4
=
[
,,,
]
ttttt
yy y yy .
Уважатимемо, що в даних відсутній явний тренд, і для простоти розглянемо модель, яка
відповідає векторній авторегресії першого порядку, описаній у п. 10.2.5. Двом
структурним рівнянням (10.26) відповідають два нормалізовані
19
коінтеграційні вектори
T
11 2
[
,1, ,0
]
aaβ
та
T
21 2
[
,1,0,
]
bbβ
.
Теоретична екзогенність у
3
та y
4
загалом відповідає поняттю сильної екзогенності у
CVAR-моделях. У VAR-моделі лише з одним лагом поняття сильної та слабкої
екзогенності збігаються. Припустимо також, що теоретичні коефіцієнти
забезпечують існування рівноваги (10.26) та виконання І(1)-умови.
Таким чином, маємо модель (10.19), у якій
13
24
00
00
α
,
11
2
2
11
0
0
ab
a
b
β
,
0
0
a
b
ρ
,
T
1, 2, 3, 4
[]
.
ttttt
yy y yy
(10.27).
Доцільно записати нашу модель у вигляді окремих рівнянь:
111,2011,121,3
31,2 0 11,1 21,4 1
(( ))
(( )).
tt tt
tttt
yyaayay
ybbyby
221,2011,121,3
4 1,2 0 1 1,1 2 1,4 2
(( ))
(( )).
tt tt
tttt
yyaayay
ybbyby
33
,
tt
y
44
.
tt
y
(10.28)
Зазначимо, що такі моделі завжди можна записати таким чином, щоб кожна
ендогенна змінна реагувала лише на одне (коінтеграційне) відношення, проте, з (10.28)
18
Останнім часом під впливом данської школи на чолі з С. Йогансеном у наукових статтях
цей термін витісняє термін VEC. Однак у текстах підручників наразі частіше вживають останній.
19
За умови, що ранг коінтеграції дорівнює 2, ця нормалізація є ідентифікуючою. Покажіть
це самостійно.
249
бачимо, що такі відношення будуть комбінаціями теоретичних відношень. Зображення
(10.28) показує, яким чином можна коригувати поведінку ендогенних змінних, якщо вони
відхиляються від стану рівноваги (у відповідь на "похибку рівноваги
20
"). Загалом кожна
ендогенна змінна
21
реагує на відхилення від рівноваги в обох теоретичних
співвідношеннях.
Ортогональні доповнення
α
та
β
мають такий вигляд:
00
00
10
01
α
,
22
11 11
22
11
11
11
.
10
01
ab
ba
ab
ba ba
ab
β
(10.29)
Отже, спільні тренди (10.22) і матриця навантаження (10.24) мають такий вигляд:
3
1
3
1
,
t
i
i
t
i
i
CT
22
11 11
22
11
11
11
.
10
01
ab
ba
ab
ba ba
ab
L (10.30)
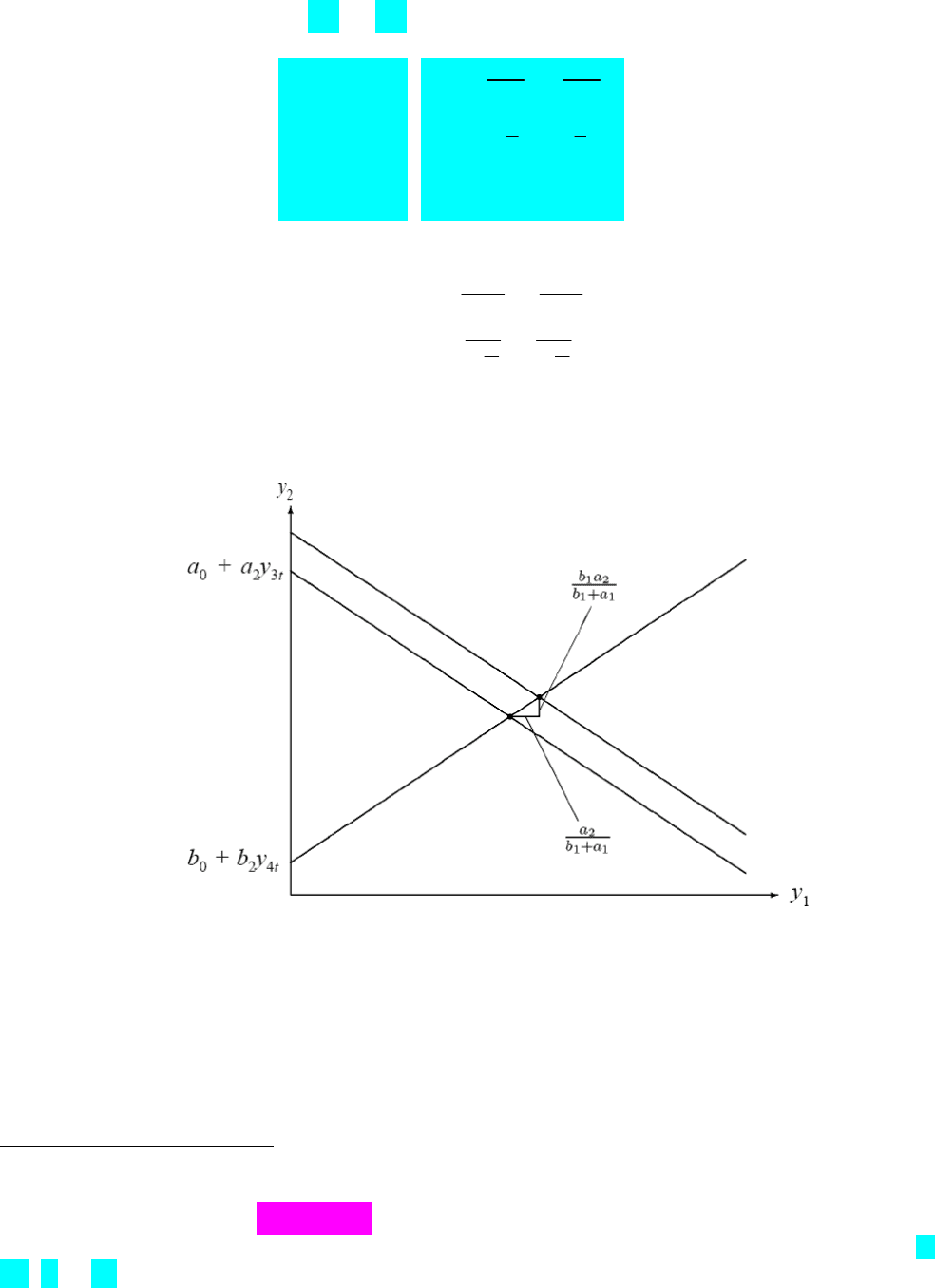
Рис. 10.2. Довгостроковий ефект одиничного зростання
3
(додатного шоку пропозиції на
ендогенні змінні у
1
та у
2
.
Далі матриця довгострокових ефектів С з формули (10.20) (матриця граничних значень
функцій імпульсної реакції) буде такою
22
:
20
Звідси, власне, походить назва моделі корекції похибок.
21
Приклад винятку:
32
0 (чому курсивом???).
22
Формула (10.31) також ілюструє той факт, що матриця С не залежить від нормування
α
,
α
,
β
та
β
.
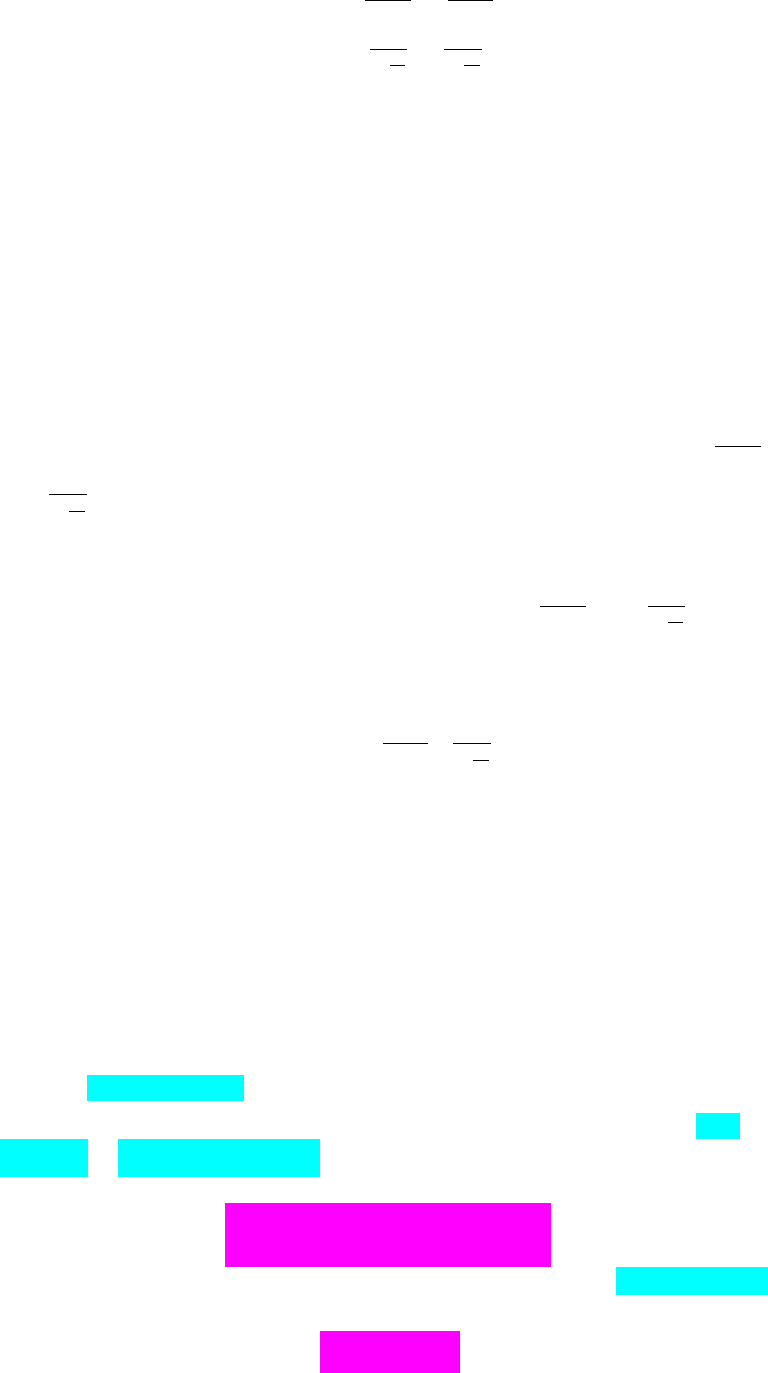
250
22
11 11
22
11
11
11
00
00
00 1 0
00 0 1
ab
ba
ab
ba ba
ab
C . (10.31)
Формула (10.30) показує, що спільні тренди відповідають кумулятивним шокам
(теоретично) екзогенних змінних у
t3
та у
t4
. Вони визначають довгострокову поведінку
ендогенних змінних. У термінах "економічного хреста" на рис. 10.1 кожний шок у
t3
та
у
t4
зсуває (назавжди) одну з кривих угору або вниз. Звідси випливає, що сума таких
шоків фактично визначає положення кривих на рис. 10.1 у момент t.
Як ми зазначали, матриця навантаження L (10.30) характеризує вплив спільних
трендів на змінні, зокрема на ендогенні змінні. Інтерпретація елементів L стає
зрозумілою, якщо скористатись "економічним хрестом" на рис. 10.1.
Розглянемо
одиничне зростання
3t
, яке відповідає одиничному зростанню
3
1
t
i
i
. З формули
(10.30) випливає, що довгостроковими наслідками будуть зміна у
1
на
2
11
a
ba
одиниць та
зміна у
2
на
2
1
1
1
a
b
a
одиниць. У термінах "економічного хреста" цю ситуацію можна
описати таким чином. Непередбачений одиничний шок ціни м'яса у
t3
, який зсуває
криву попиту на a
2
одиниць, у кінцевому підсумку призводить до зростання
рівноважних значень у
1
та у
2
на ті самі величини
2
11
a
ba
та
2
1
1
1
a
b
a
, відповідно (див.
рис. 10.2).
Так само на основі матриці С можна визначати ефекти порівняльної статики.
Наприклад, часткова похідна рівноважної ціни на курятину стосовно ціни на м'ясо,
обчислена на основі (10.26), становить
12 2
1
11
1
1
a
b
ba a
ab
, тобто дорівнює елементу (2,1)
матриці L та елементу (2,3) матриці С.
З формули (10.31) випливає, що шоки змінних у
1
та у
2
не мають довгострокового
ефекту на жодну змінну, оскільки два перші стовпчики матриці С складаються з
нулів. Цей факт можна інтерпретувати таким чином: шоки у
1
та у
2
не впливають на
положення кривих попиту та пропозиції, на відміну від шоків у
t3
та у
t4
.
Як випливає з формули (10.21), матриця С є матрицею граничних значень для функції
імпульсної реакції. Таким чином, функції імпульсної реакції описують перехідну динаміку
під час руху від одного стану рівноваги до іншого, що відбувається внаслідок шоків
відповідних змінних. Щоб вийти за межі простого опису перехідної динаміки на основі
оцінених функцій імпульсної
реакції, слід розглядати динамічні економічні моделі.
10.2.6. Метод С. Йогансена для оцінювання VECM
Припустимо, що ранг коінтеграції відомий і дорівнює r. У цьому разі існує розклад
матриці
T
αβ
, rank rank rαβ. Розглянемо для зручності модель (10.6) без
детермінованих компонентів (випадок 1, формула (10.14)) :
T
1
1
1
.
p
tt itit
i
y αβ yyε
(10.32)
Перенумеруємо елементи вибірки як 1, 2, , T , крім того, уважатимемо, що відомі
передвибіркові значення
10
,,
p
yy . Уведемо такі позначення:
1
,,
T
Yy y ,
10 1
,
T
Yyy ,
1
,
T
U εε,
11
,
p
та
01
,
T
XX X ,
де
251
1
1
1
t
t
tp
y
X
y
.
У цих позначеннях модель (10.32) набуде вигляду
T
1
.Y αβ YXU (10.33)
Для фіксованої матриці
T
αβ , як неважко побачити, оцінка найменших квадратів
ˆ
становить
TTT
1
1
ˆ
()().
Y αβ YXXX (10.34)
Підставивши знайдений вираз для
ˆ
до (10.33), після перегрупування доданків
одержимо
T
1
ˆ
YM αβ YM U, (10.35)
де
TT1
()MIXXX X. Оцінки
α
та β можна одержати за допомогою аналізу канонічних
кореляцій, або, еквівалентно, застосовуючи апарат регресії зниженого рангу до моделі
(10.35). Як показав С. Йогансен [52], оцінки можна знайти, розв'язавши таку узагальнену
проблему власних значень:
1
11 01 00 01
det( ) 0
T
SSSS , (10.36)
де
1
00
T
TSYMY
,
1T
01 1
TSYMY
,
1T
11 1 1
TSYMY
.
Позначимо впорядковані власні значення, тобто розв'язки (10.36), як
1 k
, (10.37)
а відповідну матрицю узагальнених власних векторів через
1
,,
k
Vb b. Узагальнені
власні вектори задовольняють такі рівності:
1
11 01 00 01
T
ii i
Sb SS Sb. Ці вектори нормують
таким чином, щоб
11
.
T
k
IVS V
(10.38).
Оцінка β становить
1
ˆ
,,
r
β bb,
а оцінка α є такою:
1
TT T
111
ˆˆ ˆ
ˆ
α YMY ββYMYβ . (10.39)
На основі (10.34) маємо доступну оцінку
ˆ
:
T
1
1
ˆ
ˆ
()()
TT
Y αβ YXXX . Якщо збурення
нормально розподілені, одержані оцінки є оцінками умовної максимальної
правдоподібності за умови фіксованих передвибіркових значень.
Із зауваження до теореми Грейнджера про зображення (див. п. 10.2.1) стає зрозумілим,
що знайшовши оцінку
T
β за умови нормування (10.38), ми можемо перейти до будь-якого
іншого допустимого нормування. Решту випадків, описаних у кінці п. 10.2.3, можна
розглянути за такою самою схемою.
10.2.7. Діагностика коінтеграції. Критерій Йогансена.
Перед застосуванням критерію слід визначитись із трендовими властивостями даних і
вибрати один із п'яти варіантів моделі (10.14)–(10.18). Критерій Йогансена застосовують у
двох варіантах: критерій сліду та критерій максимального власного значення.
Критерій сліду побудовано на принципі критеріїв відношення правдоподібності.
Перевіряють нульову гіпотезу: ранг коінтеграції r дорівнює
0
r (
0
0, , 1rk ) проти
альтернативи rk , де k – кількість змінних у системі, тобто альтернатива означає, що
змінні є стаціонарними. Для перевірки гіпотези слід оцінити VEC у припущенні, що ранг
коінтеграції дорівнює
0
r . Статистика сліду становить
0
0
1
ln
(
1
)
k
trace
ri
ir
LR T
,
252
де
i
задано формулою (10.37). Граничний розподіл статистики є нестандартним і
виражається як функціонал від багатовимірного вінерівського процесу [51, 52]. Критичні
значення знаходять методом Монте-Карло. Таблиці наведено в кількох роботах (критичні
значення, наведені в різних джерелах, дещо відрізняються між собою), наприклад [58].
Нульову гіпотезу можна прийняти, якщо значення статистики сліду менше за критичне.
Однак зрозуміло, що нульова гіпотеза буде прийнятою коректно, якщо ранг коінтеграції
насправді менше ніж
0
r
. Тому здійснивши перевірку лише для одного значення
0
r
, ми
фактично не можемо правильно визначити ранг коінтеграції
23
. Коректною є така
послідовна процедура. Знаходимо статистику сліду для 0
r
, 1r
і так далі, аж поки не
дійдемо до найменшого значення
r , при якому нульову гіпотезу можна прийняти. Це
значення становить ранг коінтеграції. Зазначимо, що коли прийнято гіпотезу
0r
, то ми
робимо висновок про відсутність коінтеграції. У цьому разі між змінними не існують
довгострокові рівноважні співвідношення, і коректним підходом до аналізу таких змінних
є оцінювання векторної авторегресії для різниць.
Критерій максимального власного значення. Цей критерій також побудовано на
принципі критеріїв відношення правдоподібності. Статистика максимального власного
значення, яка перевіряє нульову
гіпотезу
0
rr
проти альтернативи
0
1rr, становить
00
max
1
ln
(
1
)
rr
LR
.
Розподіл цієї статистики також є нестандартним. Нульову гіпотезу можна прийняти,
якщо значення статистики менше від критичного. Для визначення рангу коінтеграції, як
і в попередньому випадку, потрібна послідовна процедура.
Загалом можна організувати послідовну процедуру в оберненому порядку (починаючи з
1
rk). Однак, як зазначає К. Юзеліус [53], такий порядок призводить до викривлення
рівня значущості.
10.2.8. Діагностика автокореляції
Критерій портманто. Як і для необмеженої векторної авторегресії, статистику
критерію обчислюють за формулою (9.8) або (9.9). Тривалий час на практиці, у тому числі
в популярних економетричних пакетах, наприклад EViews 5.1, як розподіл Q
h
-статистики
без належного теоретичного підґрунтя використовували той самий розподіл
22
(( ))kh p
.
Однак Р. Брюґеман, Х. Люткеполь та П. Сайконен [34] нещодавно показали, що для
коінтегрованих І(1) процесів кількість степенів свободи залежить від рангу коінтеграції.
Таким чином, критерій портманто не слід використовувати для аналізу нестаціонарних
VAR-моделей (у рівнях змінних) з невідомим рангом коінтеграції. У випадку VEC-моделі,
яка не має обмежень на та Г
1;
..., Г
p–1
, а ранг коінтеграції r правильно визначений,
коректна кількість степенів свободи розподілу
2
становить
22
(1) kh k p kr
. У цьому
разі критерій портманто також слід застосовувати переважно для діагностики
автокореляції вищих порядків. Для виявлення автокореляції нижчих порядків більш
придатний LM-критерій.
LM-критерій. Для векторної моделі корекції похибок LM-критерій Бройша – Ґодфрі для
перевірки існування автокореляції збурень порядку h слід будувати майже так само, як і
для векторної авторегресії (див. п. 9.4.2, LM-критерій ). Відмінність полягає в тому, що
допоміжна модель набуває такого вигляду:
T
11 1 1 111
ˆ
ˆˆˆ
... ...
tt t ptpt htht
εαβyy y εεe ,
де
ˆ
t
– залишки вихідної моделі,
– оцінка коінтеграційної матриці вихідної моделі
(залишки допоміжної моделі
t
e , а отже, LM-статистика не залежать від способу
23
Наведені міркування є підставою для того, що в багатьох джерелах нульову гіпотезу
формулюють як "ранг коінтеграції не перевищує r
0
", що зі статистичного боку не зовсім коректно,
оскільки розподіл статистики сліду і, відповідно, критичні значення можна знайти за умови, що
ранг коінтеграції точно дорівнює r
0
.

253
нормалізації ). Значення статистики, як і раніше, знаходимо за формулою (9.11). У
випадку І(1)-змінних вона також має асимптотичний
2
-розподіл з hk
2
степенями свободи
[34]. Таким чином, на відміну від критерію портманто, цей критерій можна
використовувати для нестаціонарних VAR-моделей (у рівнях змінних) з невідомим рангом
коінтеграції
24
. Сказане дозволяє однозначно рекомендувати віддавати перевагу LM-
критерію, оскільки критерій портманто спирається на припущення про правильно
визначений ранг коінтеграції, а критерій Йогансена для визначення рангу, у свою чергу,
спирається на припущення про відсутність автокореляції.
10.2.9. Вибір довжини лага
Для вибору довжини лага в VECM можна використовувати критерії Ханана – Квіна,
або Шварца, значення яких знайдено на основі необмеженої векторної авторегресії.
Отже, значення критеріїв слід обчислювати за формулами (9.6) і (9.7). Коректність цього
підходу для інтегрованих процесів обґрунтовано в роботі [62]. Отже, на практиці слід
вибрати довжину лага за необмеженою авторегресією, а також упевнитися у
відсутності автокореляції. Після цього знайдену довжину лага можна
використовувати для визначення рангу коінтеграції.
10.2.10. Слабка екзогенність
Про зв'язок між поняттям екзогенності в економіко-теоретичному розумінні та
екзогенністю в CVAR-моделях ішлося в п. 10.2.2, тому в цьому підрозділі ми обмежимося
формулюванням гіпотези про обмеження на
α
. З алгоритмом практичної перевірки
зацікавлений читач може ознайомитись у керівництві користувача відповідної
економетричної програми, наприклад Eviews.
Гіпотеза про те, що змінна впливає на довгострокову поведінку інших змінних системи
і водночас не зазнає їхнього впливу, називається гіпотезою "відсутності оберненого
зв'язку в рівнях", або гіпотезою довгострокової слабкої екзогенності. Нульову гіпотезу
сформульовано таким чином: рядки матриці
α
, які відповідають слабко екзогенним
змінним, складаються з нулів
25
.
Задачі
Група А
Задача 10.1. Розгляньте векторний процес (x
t
,y
t
)
1
,
tt t
xx
1
(0,||1).
tttt
yxy
1. Покажіть, що x
t
і y
t
є коінтегрованими. Укажіть ранг коінтеграції та загальний
вигляд коінтеграційних векторів.
2. Запишіть процес у вигляді векторної моделі корекції похибок. Укажіть відповідні
матриці та .
Задача 10.2. Нехай у векторній моделі корекції похибок
1
1
1
p
tt itit
i
yy yε
матриця П така:
24
Тобто застосувати результати п. 9.2.4. у незмінному вигляді до необмеженої VAR-моделі.
25
В Eviews в такому випадку слід переоцінити модель, одночасно накладаючи ідентифікуючі
обмеження на і відповідні обмеження на . Так само для перевірки додаткових обмежень на
слід переоцінити модель, одночасно наклавши ідентифікуючі та додаткові обмеження.
254
161
242
321
.
Знайдіть ранг коінтеграції, матрицю коінтеграційних векторів та матрицю .
Задача 10.3. Поясніть, чому процедура С. Йогансена дозволяє не перевіряти змінні на
наявність одиничних коренів.
Задача 10.4. Нехай у векторній моделі корекції похибок
1
1
1
p
tt itit
i
yy yε
коінтеграційні вектори становлять (1; –1; 0) та (1; 1; 1), а матриця корегувальних
коефіцієнтів становить
10
02
01
.
Знайдіть матрицю П.
Група В
Задача 10.5. Користуючись матеріалами прикл. 10.3, за даними табл. 10.1, побудуйте
модель корекції похибок, попередньо визначивши порядок моделі та ранг коінтеграції.
Для нормалізації коінтеграційної матриці скористайтесь теорією, наведеною у
прикл. 10.3. Знайдіть функції імпульсної реакції та розклад дисперсії. Дайте економічну
інтерпретацію одержаним результатам.
Таблиця 10.1
(???)
Квар
тал
CPR INF
L
M
TBR
Y
1954/
Q1
2,0366
67
1,9513
79
6,354
598
1,0836
67
7,415
055
1954/
Q2
1,6333
33
0,9059
19
6,353
662
0,8143
33
7,413
609
1954/
Q3
1,3633
33
0,3596
56
6,362
623
0,8696
67
7,425
179
1954/
Q4
1,31 3,8584
45
6,363
803
1,0363
33
7,437
383
1955/
Q1
1,6133
33
3,0970
73
6,367
617
1,2563
33
7,463
076
1955/
Q2
1,9666
67
4,6957
58
6,361
511
1,5143
33
7,472
273
1955/
Q3
2,3266
67
3,7694
50
6,356
575
1,8613
33
7,483
357
1955/
Q4
2,8333
33
2,5997
20
6,352
305
2,3493
33
7,492
147
1956/
Q1
3 3,8469
96
6,346
747
2,3793
33
7,488
294
1956/
Q2
3,2633
33
2,6679
09
6,341
898
2,5966
67
7,494
708
1956/
Q3
3,35 3,5968
33
6,333
339
2,5966
67
7,496
763
1956/
Q4
3,63 2,6737
62
6,331
111
3,0636
67
7,510
212
1957/
Q1
3,63 5,4841
38
6,319
665
3,1716
67
7,515
562
255
1957/
Q2
3,6833
33
1,8741
80
6,315
313
3,157 7,514
691
1957/
Q3
3,9533
33
2,9259
91
6,307
960
3,3823
33
7,523
589
1957/
Q4
3,9933
33
0,1563
61
6,302
782
3,3433
33
7,512
344
1958/
Q1
2,8166
67
2,2797
11
6,295
580
1,838 7,490
027
1958/
Q2
1,7166
67
0,6037
13
6,305
356
1,0176
67
7,497
983
1958/
Q3
2,13 3,7484
70
6,306
495
1,7106
67
7,518
010
1958/
Q4
3,2133
33
2,7402
09
6,312
439
2,7876
67
7,539
506
1959/
Q1
3,3033
33
4,3031
24
6,308
003
2,8003
33
7,552
185
1959/
Q2
3,6033
33
3,5835
15
6,307
619
3,0193
33
7,569
154
1959/
Q3
4,1933
33
1,5468
16
6,310
843
3,533 7,565
690
1959/
Q4
4,76 0,9972
38
6,299
598
4,2993
33
7,571
422
1960/
Q1
4,6866
67
3,5010
32
6,287
990
3,943 7,589
285
1960/
Q2
4,0733
33
0,1965
90
6,285
352
3,0923
33
7,586
651
1960/
Q3
3,3733
33
1,8497
44
6,289
997
2,3903
33
7,587
665
1960/
Q4
3,27 -
1,334622
6,292
860
2,3606
67
7,581
261
1961/
Q1
3,0133
33
0,0422
49
6,297
712
2,3766
67
7,589
538
1961/
Q2
2,86 2,5560
74
6,298
597
2,3246
67
7,603
898
1961/
Q3
2,8966
67
2,2761
81
6,298
734
2,3246
67
7,618
349
1961/
Q4
3,0566
67
1,4664
58
6,304
093
2,475 7,638
439
1962/
Q1
3,2433
33
3,7014
70
6,301
269
2,739 7,651
501
1962/
Q2
3,2033
33
1,1613
40
6,304
981
2,716 7,661
856
1962/
Q3
3,3333
33
1,5811
05
6,300
118
2,858 7,669
775
1962/
Q4
3,2633
33
2,3182
76
6,299
770
2,8033
33
7,668
655
1963/
Q1
3,31 0,6098
82
6,308
603
2,909 7,682
897
1963/
Q2
3,3166
67
0,5716
96
6,316
317
2,9413
33
7,695
985
1963/
Q3
3,6966
67
1,5546
36
6,322
809
3,2806
67
7,713
159
1963/
Q4
3,9066
67
2,7898
22
6,325
236
3,4993
33
7,720
683
1964/
Q1
3,95 0,6163
32
6,330
203
3,538 7,745
479
1964/
Q2
3,9333
33
2,2662
72
6,331
433
3,4813
33
7,753
581
1964/
Q3
3,91 1,7795
44
6,343
172
3,504 7,765
315
256
1964/
Q4
4,0633
33
2,2916
63
6,350
457
3,685 7,768
110
1965/
Q1
4,3 4,2801
24
6,347
236
3,8996
67
7,787
424
1965/
Q2
4,38 1,6664
47
6,348
849
3,879 7,800
900
1965/
Q3
4,38 2,4389
49
6,354
414
3,8596
67
7,818
229
1965/
Q4
4,47 3,1800
27
6,364
606
4,1586
67
7,841
414
1966/
Q1
4,97 3,8296
60
6,372
066
4,6306
67
7,862
035
1966/
Q2
5,4266
67
4,0964
49
6,372
568
4,5973
33
7,863
805
1966/
Q3
5,79 3,0363
87
6,361
864
5,0476
67
7,873
255
1966/
Q4
6 4,5655
67
6,353
369
5,246 7,878
724
1967/
Q1
5,45 2,1182
15
6,357
935
4,5336
67
7,885
028
1967/
Q2
4,7166
67
1,2747
85
6,368
507
3,6573
33
7,889
459
1967/
Q3
4,9733
33
3,6802
91
6,381
083
4,3446
67
7,900
822
1967/
Q4
5,3033
33
4,8459
27
6,385
361
4,7873
33
7,906
584
1968/
Q1
5,58 6,0563
01
6,382
566
5,0646
67
7,920
120
1968/
Q2
6,08 4,6012
28
6,388
591
5,51 7,936
267
1968/
Q3
5,9633
33
4,6082
30
6,396
386
5,2263
33
7,943
357
1968/
Q4
5,9633
33
5,2144
79
6,404
686
5,5806
67
7,945
095
1969/
Q1
6,6566
67
4,1647
71
6,412
159
6,1376
67
7,960
184
1969/
Q2
7,54 5,3997
39
6,406
654
6,24 7,961
300
1969/
Q3
8,4866
67
5,8367
45
6,396
532
7,0466
67
7,967
107
1969/
Q4
8,62 4,6295
96
6,393
018
7,3176
67
7,963
843
1970/
Q1
8,5533
33
5,4467
23
6,390
155
7,2626
67
7,961
300
1970/
Q2
8,1666
67
6,8178
44
6,380
217
6,7523
33
7,958
402
1970/
Q3
7,8366
67
2,5651
36
6,387
072
6,3746
67
7,970
740
1970/
Q4
6,2933
33
4,4149
94
6,393
821
5,3583
33
7,963
216
1971/
Q1
4,59 7,3999
23
6,391
876
3,8633
33
7,986
131
1971/
Q2
5,04 6,2366
70
6,397
239
4,206 7,987
592
1971/
Q3
5,7433
33
4,9054
87
6,402
107
5,0503
33
7,993
721
1971/
Q4
5,0633
33
2,9647
04
6,403
958
4,2343
33
7,998
772
1972/
Q1
4,0566
67
5,5453
21
6,409
516
3,4353
33
8,018
724
