Черняк О.І. та ін. Економетрика

Подождите немного. Документ загружается.

217

Інструментами для регресора X вважають змінні Z, корельовані з X, але не

корельовані з поточними збуреннями. Щоб знайти оцінки, треба відшукати не менше

інструментів (яких немає в моделі), ніж ендогенних регресорів, тобто тих, які корельовано

з поточними збуреннями. Техніку обчислень найпростіше описати таким чином.

Оцінювання відбувається у два етапи. На першому

етапі звичайним методом найменших

квадратів оцінюють регресії ендогенних регресорів стосовно інструментів, серед яких

регресори моделі, некорельовані з поточними регресорами (екзогенні регресори). На

другому етапі також звичайним методом найменших квадратів оцінюють вихідну модель,

у якій значення ендогенних регресорів, замінюють на свої оцінки, знайдені на першому

етапі. Двохетапний метод найменших квадратів, який

застосовують для оцінювання

систем одночасних рівнянь, – це варіант методу інструментальних змінних, зумовлений

конкретним вибором інструментів. Тому зараз немає потреби розглядати коваріаційну

матрицю для цих оцінок, оскільки її наведено в розділі, присвяченому системам

одночасних рівнянь. Вибір належного набору інструментів у деяких випадках становить

складну практичну проблему, але у випадку моделей з автогегресійними

лагами завжди

можна запропонувати один очевидний розв'язок: у моделі (8.62) використати як

інструменти лагові значення X з лагом, більшим ніж k. Наприклад, у моделі (8.63)

інструментами можуть слугувати X

t-1

, X

t-2

, … .

Для коваріаційної матриці оцінок методу інструментальних змінних також існують

аналоги оцінки Неві – Веста на випадок автокорельованих збурень. За виконання

стандартних умов регулярності оцінки методу інструментальних змінних будуть

спроможними й асимптотично нормально розподіленими, хоча і не будуть асимптотично

ефективними. Однак їхня коректність не потребує припущень про структуру

автокореляції збурень (а отже, не залежить від помилок під час її визначення). Цим можна

пояснити надійність методу.

Крім того, при відомій структурі автокореляції збурень на другому етапі можна

застосувати варіант узагальненого методу

найменших квадратів, пристосований до

наявного типу автокореляції збурень.

На практиці нас частіше цікавлять оцінки параметрів вихідної форми моделі. Отже, їх

слід виразити через параметри авторегресійної форми моделі, а потім в одержані

формули підставити знайдені оцінки. Дисперсії можна знайти з використанням формули

асимптотичної дисперсії нелінійних функцій від параметрів.

Знаючи конкретну структуру

збурень (наприклад ARMA(p,q)), можна застосувати метод

максимальної правдоподібності. Вигляд функції правдоподібності у випадку MA-збурень

дуже складний, тому на практиці можуть виникати проблеми зі збіжністю.

У випадку авторегресійних збурень існує інша дуже проста можливість. Припустимо,

що в моделі (8.63) збурення генерує процес AR(1). Якщо записати (8.63) для моменту t – 1 і

з одержаного рівняння

виразити



 , підставивши в рівняння (8.63), у якому збурення

записано з використанням означення процесу AR(1), то після перепозначення параметрів

одержимо рівняння (8.64) з нелінійним обмеженням на параметри. Це обмеження

нескладно перевірити. Якщо воно хибне, то це означає, що слід обрати модель (8.64).

Іншими словами, у вихідній моделі замість геометричного слід використати розподіл лагів

Паскаля. Таким

чином, у випадку авторегресійних збурень іноді можна звільнитись від

автокореляції шляхом уведення в авторегресійну форму моделі додаткових лагів, а отже,

урешті-решт, скористатись звичайним методом найменших квадратів у модифікованій

моделі.

Оцінювання у формі рухомого середнього слід здійснювати методом максимальної

правдоподібності або нелінійним методом найменших квадратів, а отже, ми завжди

маємо спиратись на припущення про конкретну структуру автокореляції збурень. Як

завжди, найбільш поширені три ситуації: класичні збурення, AR(1)-збурення і МА(1)-

збурення. Ми обмежимось розглядом моделі з геометричним розподілом лагів із

класичними і AR(1)-збуреннями. Нам буде

зручно скористатись записом моделі у вигляді

(8.44):

(1 )

ttit







   



. (8.65)

Перетворимо (8.65) до такого вигляду:

218

(1 )

ttit







   



(1 ) ( )

XX X



   

(1 ) ( )





      .

Нехай  

M[ ]Y . Неважко побачити, що третій доданок дорівнює 

. Логічно

інтерпретувати



як невідомий параметр, тому що ми не маємо вибіркової інформації

про момент часу 0. Таким чином, модель набуває вигляду

(1 )

ttt



    ,

де

tt t

XX X X



  

(8.66)

В умовах нормально розподілених збурень логарифмічна функція правдоподібності для

цієї моделі нелінійної регресії має такий вигляд:





02 2 2

(

,,, ,

)

(

)

ln ,







      





(8.67)

де

(1 )

tt t

YX    

Аналізуючи вигляд функції (8.67), легко зрозуміти, що оцінки максимальної

правдоподібності збігаються з оцінками нелінійного методу найменших квадратів. Оцінку

дисперсії збурень знаходимо за звичною формулою











Без припущення про нормальність збурень оцінки нелінійного методу найменших

квадратів лишаються спроможними, хоча і можуть виявитись неефективними.

Для фіксованого значення  оцінки решти параметрів, тобто ,  

(

)

та



можна

знайти з лінійної регресії Y

стосовно константи

X і



. Оскільки  лежить між нулем і

одиницею, то на практиці можна застосувати решітковий пошук. Стандартно спочатку

для кожного   0,1; 0,2; ; 0,9 оцінюють лінійні регресії і в результаті вибирають

значення

 , яке дає найменшу суму квадратів залишків. На другому етапі процедура

повторюється в діапазоні  

ˆˆ

[

0,09; 0,09

]

з кроком 0,01. У разі необхідності ітерації

можна продовжувати. Правилом зупинки може бути умова, щоб різниці між двома

послідовними оцінками не перевищували заданий рівень точності. На практиці

X можна

обчислювати з використанням рекурентної формули

,XX

1tt t

XX X



 ,

2,..., .tn



(8.68)

Оцінки стандартних похибок можна знайти за допомогою оберненої до інформаційної

матриці. Остання має такий вигляд:

(,, ,, )I





  

**2

()

0000/

()

tt t

tt ttt

tt t t









 







 









 

  

, (8.69)

де

()

X  





01t





  





Вибіркові значення





також можна знайти за допомогою рекурентної формули.

Використовуючи (8.68), можна показати, що

X







219

(8.70)













 

 

3,..., .tn



(8.71)

Нарешті









(8.72)

Асимтотичну дисперсію останньої оцінки можна охарактеризувати, використовуючи

формулу асимтотичної дисперсії нелінійної функції від параметрів:

  

   

   

  

   

  

ˆˆ ˆˆ

ˆˆ ˆˆ ˆˆ ˆˆ

[] [] []

2cov

[

]

ˆˆ ˆˆ

DDD

Автокорельовані (AR(1)) збурення. Якщо збурення в (8.66) генеруються процесом

AR(1)

tt t



 

то описаний вище алгоритм можна застосувати до перетвореної моделі:



 

            

** 1

101

(1 ) (1 ) [ ] [ ] [ ] .

tt t t tt t

YY X X

При заданому значенні  у точності повторюють дії у випадку некорельованих збурень.

Для пошуку всього набору параметрів можна організувати двовимірний решітковий

пошук  і .

Задачі

Група А

Задача 8.1. За допомогою якого методу можна оцінити параметри необмеженої моделі

зі скінченною довжиною лага?

Задача 8.2. У чому полягає головна причина переходу від необмеженої моделі

розподілених лагів до моделі полиномиального розподілу лагів?

Задача 8.3. У чому полягає головна причина переходу від моделей зі скінченною

довжиною лагів до моделі з геометричним розподілом лагів?

Задача 8.4. Запишіть очікування змінної X у моделі адаптивних очікувань у вигляді

розподілених лагів для фактичних значень змінної X.

Задача 8.5. У моделі



   

0,5 0,5 0,2 0, 3

ttttt

yyxx

знайдіть значення

довготермінового мультиплікатора.

Задача 8.6. У моделі з геометричним розподілом лагів одержано оцінки:

 20,8; 0,1,2,...

i . Знайдіть середній і медіанний лаги.

Група Б

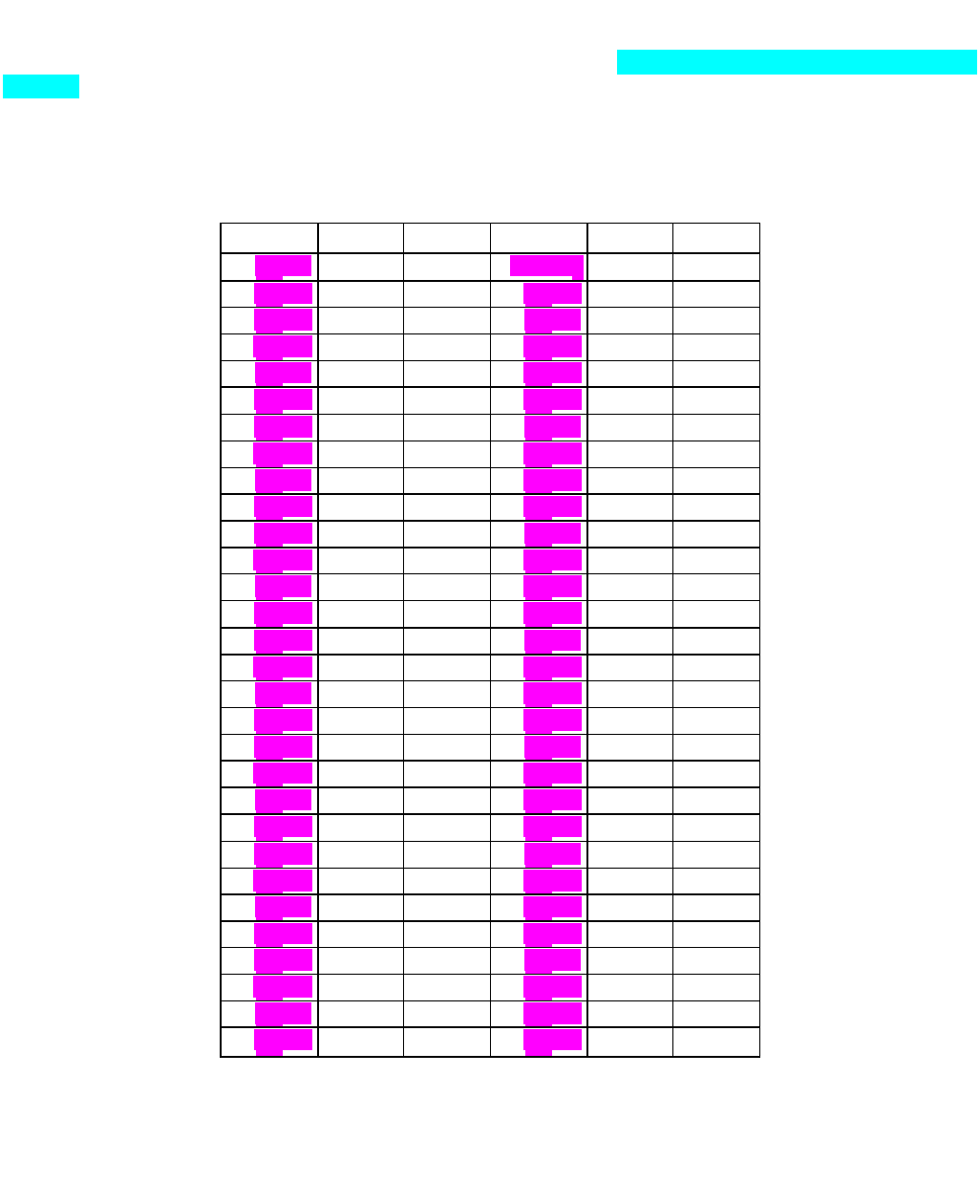
Задача 8.7. У табл. 8.1 наведено дані зі статті Ш. Алмон по промислових підприємствах

США (EXPEND – capital expenditures, капітальні витрати; APPROP – appropriations,

асигнування).

1. Побудуйте графіки обох рядів. Що можна сказати за ними про ряди? Чи помітна

залежність між рядами (у той самий період або з часовим лагом)?

2. Побудуйте крос-кореляційну функцію для лагів –12, …, 0, … , 12 (???). Зробіть

висновки.

3. Використовуючи дані табл. 8.1, оцініть необмежену модель з розподіленими лагами

220

з максимальною довжиною лага q = 6, ..., 12 для залежності EXPEND від APPROP.

Використовуючи відомі вам методи, знайдіть довжину лага.

Оцініть модель із поліноміальним розподілом лагів, що має максимальний лаг – 8 і

степінь полінома р = 2, ..., 6. Використовуючи відомі вам методи, оберіть степінь

полінома.

Таблиця 8.1

(???)

Квар

EXP

END

APP

ROP

Квар

EXP

END

APP

ROP

1953/ 2072 1660 1960/Q 2721 2131

1953/ 2077 1926 1960/ 2640 2552

1953/ 2078 2181 1961/ 2513 2234

1953/ 2043 1897 1961/ 2448 2282

1954/ 2062 1695 1961/ 2429 2533

1954/ 2067 1705 1961/ 2516 2517

1954/ 1964 1731 1962/ 2534 2772

1954/ 1981 2151 1962/ 2494 2380

1955/ 1914 2556 1962/ 2596 2568

1955/ 1991 3152 1962/ 2572 2944

1955/ 2129 3763 1963/ 2601 2629

1955/ 2309 3903 1963/ 2648 3133

1956/ 2614 3912 1963/ 2840 3449

1956/ 2896 3571 1963/ 2937 3764

1956/ 3058 3199 1964/ 3136 3983

1956/ 3309 3262 1964/ 3299 4381

1957/ 3446 3476 1964/ 3514 4786

1957/ 3466 2993 1964/ 3815 4094

1957/ 3435 2262 1965/ 4093 4870

1957/ 3183 2011 1965/ 4262 5344

1958/ 2697 1511 1965/ 4531 5433

1958/ 2338 1631 1965/ 4825 5911

1958/ 2140 1990 1966/ 5160 6109

1958/ 2012 1993 1966/ 5319 6542

1959/ 2071 2520 1966/ 5574 5785

1959/ 2192 2804 1966/ 5749 5707

1959/ 2240 2919 1967/ 5715 5412

1959/ 2421 3024 1967/ 5637 5465

1960/ 2639 2725 1967/ 5383 5550

1960/

2733

2321

1967/

5467

5465

А це що???

Джерело: Almon Shirley. The Distributed Lag between Capital Appropriations and Expenditures //

Econometrica. – 1965. –V. 33, N1 . –P. 178-196

Задача 8.8. У табл. 8.2 наведено дані про споживання та дохід у розпорядженні у

США за 1953-1984 рр.

1. Оцініть таку модель адаптивних очікувань. Споживання C

залежить від

перманентного доходу

tt tt

YC Y 

, де

задано рівнянням

()

EE E

tt tt

YY YY





Знайдіть довгострокову граничну схильність до споживання.

2. Оцініть за тими самими даними модель часткового пристосування. Бажаний рівень

споживання

C залежить від поточного доходу :

tt tt

YC Y



  , де

C –

неспостережувана змінна, підпорядкована рівнянню часткового пристосування

()

tt t t t

CC C C



 . Знайдіть довгострокову граничну схильність до споживання.

221

Таблиця 8.2

Рік,

квартал

С Y

Рік,

квартал

С Y

Рік,

квартал

С Y

1953/Q1 362,8 395,5 1963/Q4

507,5

552,5

1974/Q3 769,4

859,7

1953/Q2 364,6 401,0 1964/Q1

516,6

563,6

1974/Q4 756,5

851,1

1953/Q3 363,6 399,7 1964/Q2

525,6

579,4

1975/Q1 763,3

845,1

1953/Q4 362,6 400,2 1964/Q3

534,3

586,4

1975/Q2 775,6

891,3

1954/Q1 363,5 399,7 1964/Q4

535,3

593,0

1975/Q3 785,4

878,4

1954/Q2 366,2 397,3 1965/Q1

546,0

599,7

1975/Q4 793,3

884,9

1954/Q3 371,8 403,8 1965/Q2

550,7

607,8

1976/Q1 809,9 899,3

1954/Q4 378,6 411,8 1965/Q3

559,2

623,6

1976/Q2 817,1 904,1

1955/Q1 385,2 414,7 1965/Q4

573,9

634,6

1976/Q3 826,5 908,8

1955/Q2 392,2 423,8 1966/Q1

581,2

639,7

1976/Q4 838,9 914,9

1955/Q3 396,4 430,8 1966/Q2

582,3

642,0

1977/Q1 851,7 919,6

1955/Q4 402,6 437,6 1966/Q3

588,6

649,2

1977/Q2 858,0 934,1

1956/Q1 403,2 441,2 1966/Q4

590,5

700,7

1977/Q3 867,3 951,9

1956/Q2 403,9 444,7 1967/Q1

594,8

665,0

1977/Q4 880,4

965,9

1956/Q3 405,1 446,6 1967/Q2

602,4

671,3

1978/Q1 883,8 973,5

1956/Q4 409,3 452,7 1967/Q3

605,2

676,5

1978/Q2 901,1 982,6

1957/Q1 411,7 452,6 1967/Q4

608,2

682,0

1978/Q3 908,6

994,2

1957/Q2 412,4 455,4 1968/Q1

620,7

690,4

1978/Q4 919,2

1005,0

1957/Q3 415,2 457,9 1968/Q2

629,9

701,9

1979/Q1 921,2

1011,1

1957/Q4 416,0 456,0 1968/Q3

642,3

703,6

1979/Q2 919,5

1011,8

1958/Q1 411,0 452,1 1968/Q4

644,7

708,7

1979/Q3 930,9

1019,7

1958/Q2 414,7 455,1 1969/Q1

651,9

710,4

1979/Q4 938,6

1020,2

1958/Q3 420,9 464,6 1969/Q2

656,2

717,0

1980/Q1 938,3

1025,9

1958/Q4 425,2 471,3 1969/Q3

659,6

730,1

1980/Q2 919,6

1011,8

1959/Q1 424,1 474,5 1969/Q4

663,9

733,2

1980/Q3 929,4

1019,3

1959/Q2 439,7 482,2 1970/Q1

667,4

737,1

1980/Q4 940,0

1030,2

1959/Q3 443,3 479,0 1970/Q2

670,5

752,6

1981/Q1 950,2

1044,0

1959/Q4 444,6 483,1 1970/Q3

676,5

759,7

1981/Q2 949,1 1041,0

1960/Q1 448,1 487,8 1970/Q4

673,9

756,1

1981/Q3 955,7

1058,4

1960/Q2 454,1 490,7 1971/Q1

687,0

771,3

1981/Q4 946,8

1056,0

1960/Q3 452,7 491,0 1971/Q2

693,3

779,7

1982/Q1 953,7

1052,8

1960/Q4 453,2 488,8 1971/Q3

698,2

781,0

1982/Q2 958,9

1054,7

1961/Q1 454,0 493,4 1971/Q4

708,6

785,5

1982/Q3 964,2

1057,7

1961/Q2 459,9 500,7 1972/Q1

718,6

791,7

1982/Q4 976,3

1067,5

1961/Q3 461,4 505,5 1972/Q2

731,1

798,5

1983/Q1 982,5

1073,3

1961/Q4 470,3 514,8 1972/Q3

741,3

842,2

1983/Q2 1006,2

1082,2

1962/Q1 474,5 519,5 1972/Q4

757,1

838,1

1983/Q3 1015,6

1102,1

1962/Q2 479,8 523,9 1973/Q1

768,8

855,0

1983/Q4 1032,4

1124,4

1962/Q3 483,7 526,7 1973/Q2

766,3

862,1

1984/Q1 1044,1

1147,8

1962/Q4 490,0 529,0 1973/Q3

769,7

868,0

1984/Q2 1064,2

1165,3

1963/Q1 493,1 533,3 1973/Q4

766,7

873,4

1984/Q3 1065,9

1176,7

1963/Q2 497,4 538,9 1974/Q1

761,2

859,9

1984/Q4 1075,4

1186,9

1963/Q3 503,9 544,4 1974/Q2

764,1

859,7

Джерело: Greene W. Econometric Analysis. 3rd. edition. – Macmillan, 1997.

222

Розділ 9. Векторні авторегресії

9.1. Визначення векторної авторегресії

Моделі векторної авторегресії (VAR) являють собою природне узагальнення моделей

авторегресії на випадок багатьох змінних. Їхня перевага полягає в тому, що вони є не

лише засобом прогнозування, але й дозволяють вивчати динамічну взаємодію між

економічними змінними. Багатовимірна модель авто регресії має такий самий вигляд, як

і одновимірна, якщо відповідні символи інтерпретувати як

вектори й матриці. Таким

чином, розглянемо k-вимірний часовий ряд













,1 ,

tt tk

yyy . Модель векторної

авторегресії порядку p (VAR(p)) запишемо таким чином:



  

11ttptpt

AAy μ yyε , (9.1)

де

– k-вимірний вектор констант (



 

μ );

– матриці розмірністю kk



1,lp ;

ε – вектор збурень,



 





ttk

ε . Для різних t збурення некорельовані, тобто:

M( ) 0, .

tsεε Однак елементи

ε можуть бути корельованими між собою:



M( ) .

εε У

контексті векторної авторегресії збурення часто називають шоками, або інноваціями.

Процес

ε , що має описані властивості, називається багатовимірним процесом "білого

шуму" .

Модель (9.1) зручно записувати за допомогою матричного полінома від оператора лага

(

1tt



yy)



()

ABy ε

де

() )

AB I AB A B  .

Позначимо (i,j)-й елемент матриці

через

()l

a . Доцільно записати окремі рівняння

моделі (9.1). Розглянемо, наприклад, VAR(2) із двома змінними. Нехай



 ,

ttt

myy , де

m -

приріст логарифма агрегату М1,

y -приріст логарифма ВВП:

(1) (1) (2 ) ( 2 )

111 221

11 12 11 12

tttttt

mamayamay

  

     

(1) (1) (2 ) ( 2 )

211 222

21 22 21 22

tttttt

yamayamay

  

     

Зауважимо, що на практиці аналізовані в прикладі змінні найчастіше перетворюються

на стаціонарні саме описаним способом.

Як бачимо, окреме рівняння моделі є рівнянням регресії, у якому залежна змінна

залежить від своїх власних лагових значень та від лагових значень усіх інших змінних.

Таким чином, векторна авторегресія моделює динаміку змінних, ураховуючи їхню

взаємодію. Наприклад, вона здатна врахувати той факт, що коли Ml є більшою в одному

кварталі, то ВНП має тенденцію бути більшим у наступному кварталі, а також те, що коли

ВНП велике в одному кварталі, то ВНП має тенденцію бути більшим у наступному

кварталі. Векторні авторегресії застосовують для аналізу стаціонарних ы тренд

стаціонарних змінних. У розд. 10 ми розглянемо узагальнення векторних авторегресії на

випадок коінтегрованих І(1) змінних (див. розд. 10). У випадку відсутності коінтеграції

для таких змінних найчастіше розглядають VAR для різниць.

VAR-моделі набули популярності в прикладних економічних дослідженнях після виходу

роботи К. Сімза [66]. Їх застосовують переважно в макроекономіці. В останні 15-20 років

векторні

авторегресії поруч із векторними моделями корекції похибок стали одним з

основних засобів прикладного макроекономічного моделювання, витіснивши системи

одночасних рівнянь



З погляду статистики системи одночасних рівнянь, як і звичайна регресія, коректні лише в

умовах І(0)-змінних, тоді як зараз майже всі дослідники вважають, що основні макроагрегати

інтегровані. З емпіричного погляду головним недоліком систем одночасних рівнянь була

223

9.2 Умова стаціонарності та МА-зображення

Найзручніше розпочати з процесу VAR(1) (як і для одновимірних ARMA-процесів, для

простоти ми можемо розглядати процеси у відхиленнях від середніх і спростити

арифметику, розглядаючи моделі без константи):







1ttt

Ayyε

або



()

IABy ε

Припустимо, що матриця

()

EA має обернену матрицю, а всі власні значення матриці

А за модулем менше ніж одиниця. Тоді матричний ряд





IAA A збігається та

123

()IA EAA A





Неважко впевнитись, що формально оператор

22 33

IABAB AB



 (якщо він має

сенс) буде оберненим до 

()

IAB. Тому







    





22 33

()

ttti

IABAB AB Ay εε. (9.2)

Якщо всі власні значення матриці А за модулем менше ніж одиниця, то матричний ряд

збігається досить швидко, щоб сума ряду випадкових векторів









A ε

існувала у

розумінні збіжності в середньому квадратичному й утворювала стаціонарний процес,

який становить МА-зображення (зображення у вигляді рухомого середнього) процесу

векторної авторегресії. Зауважимо, що власні числа матриці А є оберненими величинами

до коренів полінома det( )

IAz з комплексним аргументом z .

Для розглядання загального процесу VAR(p) зручно застосувати такий прийом, як

зведення VAR(p) до VAR(1) шляхом збільшення кількості змінних у моделі:























 

























AA A

або







*** *

ttt

Ay μ y ε .

Як ми бачили кількома рядками вище, для стаціонарності потрібно, щоб власні числа

*A були менше ніж одиниця за модулем. Виявляється, що цю умову можна виразити в

термінах матричних коефіцієнтів вихідної моделі, а саме, процес VAR(p) буде

стаціонарним, якщо всі корені характеристичного полінома

  

()

det

()

zIAzAz

за модулем більше ніж одиниця. Зауважимо, що степінь

()



не перевищує (найчастіше

дорівнює) kp. При виконанні умови стаціонарності VAR(p) має МА-зображення







     





()()

tptttiti

IAB AB By εεεε. (9.3)

Матричні коефіцієнти

 можна знайти, виходячи з



A , або можна застосовувати

рекурентні підстановки до (9.1), а потім зібрати коефіцієнти при

ti

ε . Зауважимо, що



нездатність спрогнозувати стагфляцію в розвинених країнах у 70-ті роки ХХ ст. Разом із

занепадом у другій половині 70-х

традиційної версії кейнсіанства, яка була теоретичним

підґрунтям систем одночасних рівнянь, останні стали вважати неадекватними також з

теоретичного погляду, особливо після появи "Критики Лукаса" [56]. Детальніше з цією темою

можна ознайомитися в роботі [41].

224

I. Неважко знайти, що при виконанні умови стаціонарності вектор середніх значень

процесу має такий вигляд:



  

()(

)

IA Ay νμμ,

а МА-зображення буде таким:







  



ttiti

y νε ε

МА-зображення зручне для знаходження функції імпульсної реакції, яку ми розглянемо

в підрозд. 9.4, а також для прогнозування. Особливо зручно обчислити прогнози за

моделлю VAR(1):



()

ttk t

MAy ν y .

9.3 Оцінювання та специфікація моделі

9.3.1. Оцінювання

Оцінювання стаціонарної моделі (9.1) не становить великих проблем. Кожне рівняння

окремо можна оцінювати методом найменших квадратів (після того як обрано належну

довжину лага для зникнення автокореляції). Отже, процедури перевірок гіпотез будуть

стандартними. Можна показати, що у випадку нормально розподілених збурень МНК-

оцінювання окремих рівнянь збігається з системним методом максимальної

правдоподібності

. Логарифмічна функція правдоподібності буде такою (див., напр., [48]):

(, ) ( /2)ln(2) (/2)ln (1/2) ( ) ( ),

TT T

tt tt

lnk n









      







yx yx

де

– кількість спостережень, доступних для оцінювання;



 

[

1, , ,

]

tt tp

xy y;

[

,,,

]

AA 

9.3.2. Вибір довжини лага

Для вибору довжини лага в VAR-моделях використовують стандартні критерії,

значення яких мінімізується на множині можливих довжин

max

0, ,pp  . Загальна

форма критеріїв, побудованих за цим принципом є такою:

() ln| | ()

Cp c p, (9.4)

де 



ˆˆ

ptt

εε ,

ε – вектор залишків найменших квадратів, p – довжина лага,

()



–

функція від p , яка "штрафує" великі довжини лагів, значення

c може залежати від

розміру вибірки та є специфічним для конкретних критеріїв. Нерідко також

використовують варіант формули, у якому застосовано корекцію для невеликих розмірів

вибірки, що його запропонував К. Сімз [65]:







ˆˆ

ptt

εε

, де

km 1

– загальна

кількість параметрів в окремому рівнянні моделі. Вираз

ln| |



є незростаючою функцією

від довжини лага

, тоді як

()

p зростає зі збільшенням

. Таким чином, при виборі

довжини лага досягається баланс між цими протилежно спрямованими силами.

Найбільш популярними критеріями такого типу є:

 інформаційний критерій Акайке [27, 28]:

() ln| |

AIC p pk

 , (9.5)

де



;

 критерій Ханана – Квіна ([49, 63]):

225

2lnln

()

ln| | ,

HQ p pk



(9.6)

де

2lnln

 ;

 критерій Шварца (або Шварца – Рісанена) ([64, 67]):

() ln| |

SC p pk

 , (9.7)

де

 .

У кожному з цих критеріїв

()ppk . Позначимо через

()

pAIC ,

()

pHQ та

()

pSC довжини

лагів, вибрані згідно з AIC, HQ та SC, відповідно. Для фіксованих розмірів вибірки

16T 

реалізується така нерівність:

ˆˆ ˆ

() ( ) ( )

pSC pHQ p AIC



 .

Таким чином, при використанні AIC обрана довжина лага буде найбільшою, при

використанні SC – найменшою ([57, розд. 4, 8]). Одержане на основі HQ значення буде

проміжним. Оскільки нерівності нестрогі, то не виключено, що всі критерії вкажуть на

однакову довжину лага. Як з'ясував Й. Паулсен ([62]), критерії HQ та SC є

спроможними в тому розумінні, що довжина лага, обрана за цими критеріями,

збігається за ймовірністю або з імовірністю 1 до справжньої довжини лага VAR-моделі

при виконанні досить загальних умов, якщо

max

перевищує

. Натомість критерій

Акайке при збільшенні розмірів вибірки має тенденцію до переоцінювання довжини

лага. Таким чином, для обрання довжини лага рекомендуємо використовувати

критерій Ханана – Квіна, або критерій Шварца.

9.3.3. Діагностика автокореляції

Критерій портманто. Критерій портманто для векторної авторегресії розробив

Дж. Госкінг [50]; він являє собою безпосереднє узагальнення критеріїв Бокса й Пірса [31)

та Льюнга й Бокса [55] на випадок векторних часових рядів. Нульова гіпотеза полягає в

тому, що всі автоковаріації збурень дорівнюють нулю, тобто





M( ) 0( 1 2 )

tti

H : i , ,εε .

Альтернатива полягає в тому, що принаймні одна автоковаріація, а отже, одна

автокореляція є ненульовою. Статистика критерію ґрунтується на автоковаріаціях

залишків і має такий вигляд:







ˆˆ ˆˆ

()

hjj

Qn CCCC (9.8)

де









ˆˆ

ttj

Cn εε ,

ε – залишки. Для необмеженого стаціонарного процесу VAR(p) за

нульової гіпотези статистика Q

має асимптотичний розподіл

(( ))kh p, якщо T та h

прямують до нескінченності, а

1/2

()hOn . Як показав С. Ан [26], коли існують обмеження

на параметри, кількість степенів свободи розподілу 

дорівнює різниці між кількістю

(неодночасних) автоковаріацій (k

h), які фігурують у статистиці Q

, та кількістю оцінених

параметрів VAR-моделі.

Для поліпшення властивостей критерію для малих вибірок Дж. Госкінг у згаданій

роботі запропонував також використовувати модифіковану статистику:









211

ˆˆ ˆˆ

()

hjj

Qn CCCC

(9.9)

Зазначимо, що вибір h також суттєво впливає на властивості критерію в умовах малих

вибірок. З одного боку, щоб граничний розподіл був якісною апроксимацією, h має бути

значно більшим за p. З іншого боку, вибір надто великого значення h може спричинити

втрату потужності критерію. Часто на практиці розглядають кілька значень h. Критерій

портманто слід застосовувати передусім для діагностики автокореляції вищих порядків.

226

Для виявлення автокореляції нижчих порядків більш придатний LM-критерій, який ми

розглянемо підрозд. 9.4.

LM-критерій. Критерій множників Лагранжа (LM-критерій), також відомий як

критерій Бройша – Ґодфрі [33,45], як і в одновимірному випадку, перевіряє існування

автокореляції збурень порядку h. Розглянемо таку модель для збурень вихідної векторної

авторегресії:





 

...

tt htht

BBεε εe ,

де

– (векторний) білий шум.

Критерій полягає в перевірці нульової гіпотези (сформулюйте по-іншому,

наприклад: Для визначення критерію Слід перевірити нульову гіпотезу

 

H : B B (відсутність автокореляції) проти





{1, , } : 0

H : i h B . Відповідну

LM-статистику обчислюють на основі такої допоміжної моделі:





  

11 11

ˆˆˆ

... ... ,

tt ptpt htht

AABBε yyεεe (9.10)

де

ε – залишки вихідної моделі;



e – збурення допоміжної моделі. Значення

ε при 0t



слід заповнити нулями. Позначимо залишки з оціненої допоміжної моделі через



 

(

)

tT та визначимо









ˆˆ

ett

ee . Тоді значення LM-статистики можна обчислити за

такою формулою:











ˆˆ

()

LM u e

Qnk . (9.11)

За нульової гіпотези статистика асимптотично має



-розподіл з hk

степенями

свободи [34]. Д. Еджертон та Г. Шукур [42] здійснили широкомасштабне дослідження

методом Монте-Карло і виявили, що для малих вибірок розподіл статистики може значно

відрізнятись від асимптотичного 

-розподілу. Вони запропонували F-версію критерію,

яка має ліпші властивості в умовах малих вибірок.

9.4. Функція імпульсної реакції

Функція імпульсної реакції – траєкторія

y , яка реалізується в результаті одиничного

шоку 

,ti

, тобто,

,, ,

0, 1, 0,

tsi ti tsi





 для



. Таким чином, у моделі з k

змінними існує загалом k

імпульсних реакцій. Ця функція цікава з кількох причин. По-

перше, це – альтернативна характеристика поведінки наших моделей. По-друге, вона

дозволяє починати аналіз "причин" і "ефектів". Наприклад, на основі VAR-моделі, у якій

фігурують ВВП і M1, можна обчислити реакцію ВВП на грошовий шок і інтерпретувати

результат як "ефект" монетарної політики

на ВВП. Ми детально ознайомимося із

застереженнями стосовно цієї інтерпретації, але зрозуміло, що слід вивчити, як

обчислювати імпульсну реакцію.

Запишемо векторне MA-зображення як







 



titi

Iy νε . Тоді послідовність

матричних коефіцієнтів 

{,,}визначає всі функції імпульсної реакції в моделі.

Позначимо (j, l)-й елемент матриці



через

()i



. Послідовність

()

,0,

i визначає

функцію реакції j-ї змінної на одиничний шок l-го рівняння моделі

. Зазначимо, що

функції імпульсної реакції в стаціонарних векторних авторегресіях завжди збігаються до

нуля. Цей факт є елементарним наслідком умови стаціонарності.



Ми уникаємо формулювання "функція імпульсної реакції j-ї змінної на одиничний шок l-ї

змінної" з причин, які стануть зрозумілими в наступних підрозділах.