Черняк О.І. та ін. Економетрика

Подождите немного. Документ загружается.

207

8.2. Типи моделей регресії з лаговими змінними

Моделі регресії з лаговими змінними розрізняються на таки типи:

У моделях з розподіленими лагами (МРЛ) регресорами є лише поточні та минулі

значення незалежним змінних. Наприклад, у випадку лише однієї незалежної змінної

модель має вигляд

01122

ttttktkt

YXXXX

 

     (8.16)

Залежно від кількості k лагових значень незалежної змінної моделі з розподіленими

лагами розділяються на два типи:



моделі зі скінченними лагами

;

titit





  



(8.17)



моделі з нескінченними лагами

titit







  



(8.18)

В обох випадках щоб уникнути прямування

MY до нескінченності, припустимо, що

сума коефіцієнтів



скінченна:





(8.19)

Рівняння (8.4), (8.7), (8.13), (8.15) є прикладами моделей із розподіленими лагами.

Авторегресійні, або динамічні моделі. У цих моделях множина регресорів містить

одне або більше лагових значень залежної змінної. Наприклад,

122

ttttt

YXYY



    (8.20)

Інтерпретуємо регресійні коефіцієнти в моделях із розподіленими лагами на прикладі

моделі (8.16). У цій моделі за рівності решти умов, якщо Х

збільшиться на одиницю за

період

t , то

MY зміниться на

 у момент t , на



у момент 1t



і так далі. Визначимо

такі характеристики впливу:



частковий мультиплікатор порядку i. Він характеризує граничний ефект



на

Y , тобто

tt i

dY dX



 . Іншими словами, частковий мультиплікатор характеризує

вплив

MY одиничного зростання Х

, яке відбулось за i періодів до періоду t ;



короткостроковий, або миттєвий мультиплікатор. Це частковий

мультиплікатор порядку

i = 0, що дорівнює



. Тобто він характеризує вплив на

одиничного зростання Х

, яке відбулося в той самий період;



проміжний мультиплікатор порядку i. Його визначають як суму i перших

часткових мультиплікаторів

...

 . Проміжний мультиплікатор характеризує

вплив на

MY від зростання Х

на одиницю протягом i періодів перед t ;



довгостроковий, загальний, або рівноважний мультиплікатор, який визначають

як суму всіх часткових мультиплікаторів

i 







. Рівноважний мультиплікатор

характеризує ефект

MY від зростання Х

на одиницю в кожному періоді, який

передує t .

Корисно також розглянути таке. Припустимо, що весь час X

= c , у момент t X зросте

на 1, а потім повернеться до попереднього рівня. Тоді



характеризуватиме різницю між

МY

t+i

і МY

, тобто розподіл реакції в часі на короткостроковий шок і швидкість повернення

Y до попереднього рівня (пригадаймо, що 

= 0 починаючи з деякого k у моделях зі

скінченними лагами і 

0 при i). Тепер припустимо, що весь час X

= c , у момент t X

зросте на 1 і залишиться на цьому рівні. Надалі будемо називати таку ситуацію

збереженим зростанням. У такому випадку повна сума лагових коефіцієнтів

характеризує різницю між рівноважними значеннями MY, які відповідають вихідному і

208

новому значенням X, тобто довгострокову, або повну реакцію, а часткові суми показують,

з якою швидкістю y реагує на зміну X.

Оскільки часткові мультиплікатори дорівнюють регресійним коефіцієнтам, то вони

залежать від одиниць виміру незалежної змінної Х

Як характеристику, вільну від одиниць виміру, розглядають стандартизовані

коефіцієнти, або лагові ваги







для 0,1,2,...ik



. (8.21)

Після підстановки (8.21) до (8.18) або (8.19) модель набуде такого вигляду

titit

YwX





 



. (8.22)

Розглянемо кілька інших статистик, які характеризують розподіл лагів.

Середній лаг

Wiw





визначає швидкість, з якою

Y реагує на зростання зі

збереженням Х

на одиницю за період за умови, що всі регресійні коефіцієнти додатні.

Інша ситуація, коли зручно скористатись цим показником – та, коли виникає потреба

одним числом охарактеризувати затримку в часі реакції на миттєвий шок.

Медіанний лаг визначає час, за який відбувається 50 % зміни

у відповідь на

зростання зі збереженням Х

за період







min .

w: w ,

median lag w

8.3.Оцінювання моделей із розподіленими лагами

Для зручності розглянемо модель з однією незалежною змінною

titit





  



. (8.23)

Існують два підходи до оцінювання МРЛ: необмежений і обмежений.

Необмежений підхід використовують, якщо довжина лага

k скінченна і немає

обмежень стосовно характеру лагової залежності, накладених на регресійні коефіцієнти

моделі. Застосовуючи такий підхід, ситуації розрізняють залежно від того, відома чи

невідома довжина лага.

Обмежений підхід використовують, якщо на регресійні коефіцієнти накладено

обмеження, які стосуються характеру лагової залежності. Ми розрізнятимемо два

випадки:



скінченна довжина лага;

 нескінченна довжина лага.

Необмежене оцінювання МРЛ

. Припустимо, що збурення задовольняють класичні

умови. У такому випадку можна застосувати звичайний метод найменших квадратів

(ЗМНК), причому оцінки ЗМНК будуть найкращими лінійними незміщеними оцінками.

Необмежене оцінювання МРЛ у випадку невідомої довжини лага.

Найчастіше

довжина лага в моделі (8.23) невідома, тому її слід визначити.

Існують різні методи визначення довжини лага. Найбільш популярним серед них є

підхід, за якого оптимізують певну формальну характеристику. При цьому

використовують такі критерії:



максимізація виправленого коефіцієнта детермінації

(

)



 



;



мінімізація інформаційного критерію Акайке

ln( )

SSR q

AIC

;



мінімізація критерію Шварца

209

()

ln ,

SSR q

SC q



де

n – кількість спостережень;

– кількість коефіцієнтів у регресійній моделі; SSR – сума

квадратів залишків.

Усі ці критерії побудовано на компромісі між максимізацією

R , який зростає при

збільшенні кількості змінних у моделі, і принципом економності, тобто недопущенням

розростання моделі. Найбільш чуттєвим до залучення додаткових лагів є критерій

Шварца (при ln

()

2n  ), а найменш чуттєвим – критерій максимізації

R .

Беручи до уваги той факт, що довжина більшої частини рядів економічних даних

коротка, можна окреслити дві серйозні проблеми, які виникають у випадку великої

довжини лага:

1. Невелика кількість ступенів свободи.

Чим більша довжина лага, тим менше кількість ступенів свободи і, отже, тим меншою є

точність оцінок і надійність перевірок гіпотез.

Мультиколінеарність.

Чим більшою є довжина лага, тим із більшою ймовірністю додаткові лагові змінні

будуть корельованими. Мультиколінеарність також знижує точність оцінок і надійність

перевірок гіпотез.

Підводячи підсумок, можна сказати, що внаслідок ненадійності перевірок гіпотез

збільшення довжини лага помилково призводить до висновку при незначущість

коефіцієнтів.

З метою розв'язання цієї проблеми на регресійні

коефіцієнти накладають обмеження.

8.4. Обмежене оцінювання скінченних МРЛ

За способом накладення обмежень розрізняють моделі з довільно розподіленими лагами

і моделі з поліноміально розподіленими лагами.

8.4.1. Моделі з довільно розподіленими лагами

При застосуванні такого підходу визначення ваг лагових змінних ґрунтується на

певних припущеннях щодо розподілу і часу реакції залежної змінної на зміну незалежної

змінної. Найчастіше використовують такі моделі:

1. Арифметично розподілені ваги.

У цій моделі, яку запропонував Фішер, ваги лінійно спадають:















(1), 0

kii=,k

i>k

(8.24)

Модель ґрунтується на ідеї, що більш недавні значення залежної змінної мають

сильніший вплив, ніж більш давні.

Підставивши (8.24) до (8.23), одержимо

(1) ,

ttittt

YkiX Z





     



(8.25)

де

(1)

tti

ZkiX









Модель (8.25) оцінюють звичайним МНК.

Позначимо через b МНК-оцінку . Тоді

(

)

kib  



для 0,1,...,ik



де





– оцінка

 .

Розподіл ваг "обернене V ".

У цій моделі, що її запропонував Ф. ДеЛеув, ваги спочатку лінійно зростають, а потім

спадають:

210

 





    







(1 ) , 0 2

(

)

, 1 .

iik/

ki +ik

i>k

(8.26)

Підставивши (8.26) до (8.23), одержимо

0(/2)1

[(1) (1) ] ,

tt tittt

iik

YiXkiXZ





       



(8.27)

де

0(/2)1

(

)(

)

tti t

iik

ZiX kiX





  



Модель (8.27) оцінюють звичайним МНК, після чого, як і в попередньому випадку,

коефіцієнти вихідної моделі знаходять за формулами

(1 ) 0 2,

(1) 2,

ib i= , k/

kibi=k/, k

 

  

де b – оцінка  .

Розглянутий підхід має такі обмеження:

Структура ваг має бути апріорі відомою, тобто чи ваги зростають, чи спадають, чи

наслідують схемі "оберненого V " тощо.

Тип залежності ваг також має бути відомим апріорі, тобто, наприклад, якщо ваги

спадають, то чи це спадання лінійне, експоненційне тощо.

Його перевагами є:

1. Простота оцінювання.

2. Можливість знаходити довжину лага з використанням простих статистичних

критеріїв, наприклад

R , AIC, SC.

8.4.2. Поліноміальний розподіл лагів

У будь-якій моделі з довільними лагами коефіцієнти



утворюють певну функцію

лагового індексу i . Оскільки обирати цю функцію треба апріорно, то зрозуміло, що цей

вибір може бути хибним.

Одним із методів усунення цього недоліку є застосування моделей з поліноміально

розподіленими лагами. Цей метод запропонувала Ширлі Алмон.

Основна ідея цього методу полягає в тому, що "справжня" функція

()

i

може бути

достатньо точно наближеною поліномом порядку

до лагового індексу i :

01 2

...

ii i     для 0, .rkr



 (8.28)

Підставивши (8.28) до (8.23), одержимо

101

(...)

titt rtit

YX iiX





        



або, якщо формально записати

01 , то

00 0 0

kr r k

t j ti t j ti t

ij j i

YiX iX



  

     

  

00 11 ,

...

tt rrtt

ZZ Z



     (8.29)

де

0tt

ZX ,

2...

tt t tk

ZX X kX

 

  для 1,

r .

Якщо збурення задовольняють класичні умови, то в моделі (8.29) оцінки ЗМНК будуть

найкращими незміщеними лінійними оцінками.

Позначимо через

a МНК-оцінки



. Тоді оцінки коефіцієнтів



такі:

    

01 2

...

aaiai ai для 0,ik . (8.30)

Оцінки (8.30) є оцінками МНК з обмеженнями.

Дисперсії

 легко знайти:

211

(

... ,

)

2cov

(

)

rj jh

ijjh

jjh

Db D a a i a i i Da i a a





 



(8.31)

для

0,ik

На коефіцієнти



зазвичай накладають додаткові обмеження, які називаються

"крайовими обмеженнями", а саме:





 і

k 



 . (8.32)

З урахуванням (8.28) ми можемо сказати, що

-1 0 1 2

βααα... ( 1) α 0.

 

(8.33) (де 8.32???)

101 2

βαα(1)α ( 1) ... α (1)0.

kk k



      (8.34)

У різних ситуаціях накладають одне або обидва обмеження (8.33) і (8.34). Ці обмеження

є лінійними обмеженнями на коефіцієнти моделі (8.29).

Отже, щоб оцінити модель (8.29), слід записати модель з обмеженнями й оцінити її,

використовуючи ЗМНК.

Після знаходження

a оцінки коефіцієнтів



слід обчислювати так само, як і в

попередньому випадку.

Варто нагадати, що в результаті накладення обмежень зміняться оцінки всіх

коефіцієнтів моделі.

Досі ми вважали довжину лагів і порядок полінома відомими. У реальних ситуаціях ці

величини невідомі, отже, потрібні методи їх визначення.

Визначення довжини лагів. Спочатку модель треба оцінити з використанням

необмеженого підходу, отже, для визначення довжини лагів використовують методику,

розглянуту раніше у підрозд. 8.3

Визначення порядку полінома.

Після того, як довжину лагів k визначено, порядок

полінома

rk . Потім послідовно знижуємо порядок полінома на 1 і здійснюємо вибір на

основі попередньо визначеного критерію (

,,RAICSC). На практиці зазвичай остаточний

порядок полінома рідко буває більше ніж 3.

Проблема неправильної специфікації.

Проблема неправильної специфікації

виникає, коли неправильно визначено довжину лагів і порядок полінома (однієї з цих

величин, або обох одночасно).

Позначимо через k визначену довжину лагів, а через *k – справжню довжину. Якщо

*kk (залучення зайвих змінних), то оцінки незміщені і спроможні, але неефективні.

Якщо

*kk

(не залучено важливі змінні), то оцінки зміщені ті неспроможні.

Позначимо через r визначений, а через *r – справжній порядок полінома. Якщо *rr



(накладення некоректних обмежень), то оцінки зміщені і неспроможні. Якщо *rr

(перепараметризація моделі), то оцінки будуть незміщеними, але неефективними.

8.5. Моделі з нескінченною довжиною лагів

Моделі зі скінченною довжиною лагів ґрунтуються на припущенні, що вплив лагових

значень незалежної змінної

X на залежну змінну незначний для великих лагів, отже,

відповідні коефіцієнти дорівнюють нулю.

Однак, як ми з'ясували вище, неправильне визначення довжини лага, тобто різниці в

часі, після якої впливами можна знехтувати, призводить до проблем з оцінюванням.

Проблеми неправильного визначення довжини лага немає в моделях з нескінченною

довжиною лагів (8.18). Для зручності

нагадаємо відповідне рівняння:

titit







  



αβ ε

titit











. (8.35)

Під час спроби оцінити коефіцієнти моделі (8.35) виникає нова проблема: як оцінити

нескінченну кількість параметрів

 з використанням скінченної кількості спостережень.

Для розв'язання цієї проблеми існують кілька методів.

212

8.5.1. Геометричний розподіл лагів (розподіл Койка)

Ця модель є найбільш популярною в емпіричних дослідженнях моделей із

розподіленими лагами.

Модель запропонував Л. Койк, який припустив, що вплив лагових значень X на

експоненційно спадає з часом. Іншими словами, регресійні коефіцієнти утворюють

спадну геометричну прогресію:

, 0< <1

 

ββ,0 λ 1



 для 0,1,...,in



0,1,...,in



. (8.36)

Чим ближче  до нуля, тим швидше спадає вплив попередніх лагових значень.

У результаті підстановки (8.36) до (8.35) одержуємо

ttit







  



αβ ε.

ttit













(8.37)

Запишемо (8.37) для моменту 1t  :

10 11

ttit







  



10 11

αβ λ ε.

ttit





 



 



(8.38)

Помножимо (8.38) на



і віднімемо від (8.37)

(1 )

tt ttt

YY X



     

λα(1 λ) βελε.

tt ttt

YY X



  (8.39)

Перенесемо

Y

у праву частину рівняння

00 1tttt

YXY





  , (8.40)

де

0t1

(1 ) ; .

tt

 

Оскільки модель (8.40) містить лагове значення



залежної змінної, то вона належить

до класу авторегресійних або динамічних моделей. Збурення





 

t1tt

є процесом

рухомого середнього першого порядку (МА(1)).

Обчислимо характеристики впливу, уведені в підрозд. 8.3.

Середній лаг









 



 

  









/(1 )

1/(1 ) 1

w (8.41)

Медіанний лаг























 





 

 







min min :

(1 ) / (1 )

10,5.

1/(1 )

w: w ,

median lag w w

Тобто медіанний лаг можна визначити з рівняння 10,5

  , або 0,5

 , звідки



ln0,5

median lag (8.42)

Миттєвий мультиплікатор дорівнює



Рівноважний мультиплікатор:





    







(8.43)

Якщо в моделі

titit







  



замість (8.36) записати

213

(1 )



 

(8.44)

то  слід інтерпретувати як рівноважний мультиплікатор. Тому деякі автори віддають

перевагу останньому формулюванню моделі.

8.5.2. Розподіл лагів Паскаля

Цю модель запропонував Р. Солоу.

Коефіцієнти



в основному рівнянні (8.35) визначають таким чином:

w для 0,1, 2,...i



, (8.45)

де

(1)!

(

)(

)

!( 1)!

iri ri

iir



  



(факторіал ки оклику???)

(8.46)

де

r - натуральне число, 0 1 .

На відміну від моделі з геометричним розподілом лагів, у якій коефіцієнти



монотонно спадають, тепер коефіцієнти наслідують схемі "оберненого V".

Для того щоб записати модель з розподілом лагів Паскаля підставимо (8.45) до (8.35)

(1)

(

)[

...

]

ttttt

YXrXX





        (що це за знаки оклику???)

(8.47)

У моделі (8.47) невідомі параметри



,,,r . Зауважимо, що модель з геометрично

розподіленими лагами є частковим випадком (8.47) при 1r



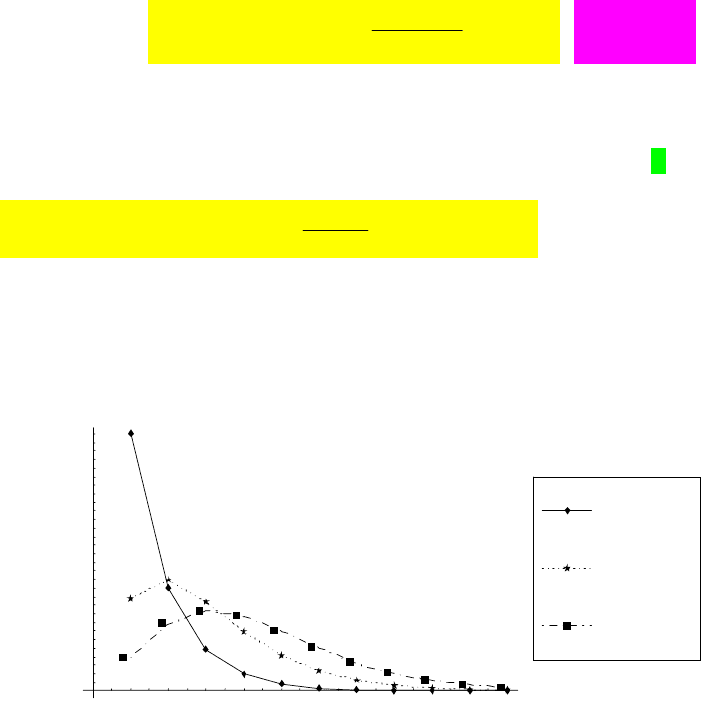
Вплив параметра

на характер розподілу лагів проілюстровано на рис. 8.2, де

зображено графік вагових коефіцієнтів для 0, 4



 і 1, 3, 5r



, відповідно.

2 4 6

0.1

0.2

0.3

0.4

0.5

0.6



Рис. 8.1

Модель з розподілом лагів Паскаля також можна записати у вигляді авторегресійної

моделі. Згадаймо, що однією з основних переваг моделей з розподіленими лагами є

можливість досліджувати розподіл у часі реакції залежної змінної на зміну визначальних

факторів. Причиною введення структур розподілів лагів, які ми розглянули, були такі

недоліки моделей з необмеженими лагами, як

мультиколінеарність і необхідність

визначати максимальну довжину лага (надійність статистичних методів визначення

максимальної довжини лага також зменшується внаслідок мультиколінеарності).

Проблема максимальної довжини лага стосується і моделей з поліноміально розподіленими

лагами. Моделі з геометричним розподілом лагів спираються на припущення, що

величина реакції із самого початку монотонно спадає в часі. На практиці таке

припущення виконується далеко не завжди. Наведемо такий тривіальний приклад.

Припустимо, що ми використовуємо щомісячні дані, а максимальна реакція виявляється

через чотири місяці. Зрозуміло, що в цьому разі найбільший коефіцієнт має бути при Y

t-4

Таким чином, на нашу думку, розподіл лагів Паскаля – найбільш гнучкий засіб

моделювання серед тих, що ми розглянули, хоча, як ми побачимо у підрозд. 8.6, у деяких

214

випадках вигляд розподілу лагів можна вивести з економічних міркувань. У наступному

підрозділі ми розглянемо подальше узагальнення розподілу лагів Паскаля.

8.5.3. Моделі з раціонально розподіленими лагами

З використанням оператора лага (див. підрозд. 7.4) основна модель (8.35) набуде

вигляду

()

titititt tt

YX BX BX









     



(8.48)

де

01 2 3

() ...

BB BBB





  



(8.49)

поліном стосовно B .

Вираз









є збіжним степеневим рядом. Тому його можна проінтерпретувати як

розклад у ряд Тейлора функції

()

B . Д. Йоргенсон запропонував розглянути моделі, у яких

функція

()

B раціональна, тобто

01 2

...

()

...

BB B

   



 



   

(8.50)

Підставимо (8.50) до (8.48), поклавши



 :

()

ttt





 



Помножимо обидві частини останньої рівності на

()



() () () (),

ttt

BY B B X B 

звідки

00 11 11

... ...

tttptptqtqt

YXX XYY





        , (8.51)

де

() (

1...

)

B  

()

... .

tttt qtq



        (8.52)

Рівняння (8.51) задає модель із раціонально розподіленими лагами в авторегресійній

формі. Ця модель узагальнює дві розглянуті раніше моделі. Поклавши в (8.51)

()B і

()1BB, одержуємо модель з геометрично розподіленими лагами. Модель із

розподілом лагів Паскаля одержуємо, якщо

() (1 )



 і () (1 )

BB.

8.6. Моделі з нескінченною довжиною лагів і економічна теорія

Усі моделі з нескінченою довжиною лагів, розглянуті вище, удалося привести до

авторегресійної форми.

Відповідні перетворення мали технічний характер, оскільки їх було здійснено з метою

позбутися нескінченної кількості невідомих параметрів у моделях. У цьому розділі ми

розглянемо приклади з економічної теорії, які безпосередньо призводять до

авторегресійної форми моделей із розподіленими лагами.

8.6.1. Модель часткового пристосування

Цю модель запропонував Марк Нерль. Він припустив, що поточний рівень пояснюючої

змінної

визначає "бажаний" рівень залежної змінної

YX (8.53).

Наприклад, бажаний рівень запасів фірми є функцією від рівня продажів, а бажаний

рівень капіталу в економіці є функцією випуску.

215

Однак бажаний рівень не можна спостерігати і, отже, використовувати для

оцінювання. З різних причин існує різниця між бажаним і фактичним рівнями залежної

змінної:

().

tt t t t

YY Y Y







   (8.54)

Тобто з точністю до збурення фактичний приріст залежної змінної

1tt



 буде меншим

від бажаного в



разів.

Рівняння (8.55) відоме як рівняння часткового пристосування, а  називається

коефіцієнтом пристосування.

Чим

(1 )

tt tt

YX X





    ближче до одиниці, тим швидше фактичний рівень

наближається до бажаного.

Запишемо (8.54) у такому вигляді:

(1 ) .

tt tt

YY Y







 

(8.55)

З (8.55) видно, що фактичне значення залежної змінної в момент t дорівнює зваженому

середньому її бажаного значення в момент

t і фактичному значенню в момент 1t



Підставимо (8.53) до (8.55):

()(1)

tttt

YXY



    .

Звідси

(

)

ttyt

YXY



    (8.56)

Якщо не брати до уваги властивості збурень, то (8.56) є авторегресійною формою

моделі з геометричним розподілом лагів.

8.6.2. Модель адаптивних очікувань

У моделі адаптивних очікувань, яку запропонував П. Кейган, "очікуваний" рівень

пояснювальної змінної



визначає поточний рівень залежної змінної

Y :

ttt





  (8.57)

Наприклад, сукупний попит на гроші є функцією очікуваної довгострокової відсоткової

ставки, обсяг попиту є функцією очікуваної ціни, рівень споживання є функцією

очікуваного, або перманентного доходу.

П. Кейган припустив, що очікувані значення можна коректувати з урахуванням нової

інформації:

( ), 0< 1.

tt tt

XX XX

 



 

(8.58)

Оскільки  0< 1, то зміна очікуваного рівня

1tt





 завжди менша, ніж різниця між

фактичним значенням



і його очікуваним значенням





Рівняння (8.58) відоме як "рівняння адаптивних очікувань", або "рівняння навчання на

похибках".

Коефіцієнт  називається "коефіцієнтом очікувань". Чим більше  , тим більшою

мірою реалізуються очікування в період

У крайньому випадку 1



 усі очікування реалізуються протягом поточного періоду.

Запишемо (8.58)у такому вигляді:

(1 ) ,

tt t

XX X





   (8.59)

звідки видно, що очікуване значення є зваженим середнім фактичного і попереднього

очікуваного значення.

Підставимо (8.59) до (8.57):

(1 ) .

tt tt

YX X





    (8.60)

Запишемо (8.60) для моменту

1t 

, результат помножимо на (1-



) і віднімемо від (8.59):

(1 ) (1 ) .

ttttt

YXY



      (8.61)

Таким чином, ми одержали модель з геометрично розподіленими лагами, записану в

авторегресійній формі. Якщо збурення у вихідній моделі (8.57) – класичні (тобто

гомоскедастичні та некорельовані), то збурення в моделі, записаній у вигляді (8.61)

генерує процес MA(1). Однак не слід думати, що модель адаптивних очікувань із

216

необхідністю веде до появи автокорельованих збурень в авторегресійній формі моделі.

Наприклад, якщо в (8.57)



= (1 –



)



t–1

+ u

, то u

являють собою збурення в моделі (8.61).

Зрозуміло, що u

можуть бути некорельованими і гомоскедастичними. Оскільки апріорі

невідомо, які властивості мають збурення вихідної моделі в конкретних ситуаціях, то зі

сказаного можна зробити висновок, що та чи інша економічна модель, яка призводить до

моделі з геометричними лагами, взята окремо, не визначає властивості збурень в

авторегресійному вигляді останньої. Отже, на нашу думку,

правильним підходом буде

статистичне визначення властивостей збурень у кожній конкретній ситуації.

8.7. Оцінювання моделей з нескінченною довжиною лагів

У цьому підрозділі ми коротко і досить неформально розглянемо методи оцінювання

моделей з раціональними лагами, приділяючи основну увагу найпростішому випадку –

моделям з геометричним розподілом лагів. Відразу наголосимо, що необхідною умовою

спроможності оцінок методу найменших квадратів і оцінок інших методів є

стаціонарність змінних моделі. Отже, важливо пам'ятати, що моделі з розподіленими

лагами є засобом дослідження зв'язків між

стаціонарними змінними. У протилежному

випадку іноді вдається відшукати "стабілізуючі" перетворення, наприклад перехід до

різниць (як під час моделювання Бокса – Дженкінса), або до відносних приростів.

Звернімо увагу на те, що в прикладах, розглянутих на початку розділу, деякі змінні

відразу мали вигляд приростів, що було продиктовано теорією, покладеною в основу

відповідних моделей. Якщо змінні

стають стаціонарними в результаті виділення

детермінованого тренда, наприклад лінійного, то проблему можна розв'язати шляхом

введення в модель відповідного тренда. Найбільш уживаним способом дослідження

залежностей між нестаціонарними змінними є модель корекції похибок.

Як було зазначено вище, моделі з (раціонально) розподіленими лагами можна

записувати у двох формах: авторегресійній і рухомого середнього. Тому

оцінювати модель

можна в будь-якій із цих форм.

Оцінювання в авторегресійній формі. Авторегресійна форма моделі з раціонально

розподіленими лагами у випадку єдиної пояснювальної змінної має вигляд

titiitit

YXY







    



, (8.62)

де



– збурення, а кількості k–1 i l лагових значень визначають, на відміну від випадку

необмежених лагів, вихідним виглядом моделі (у формі рухомого середнього). Наприклад,

як ми побачили в підрозд. 8.6, авторегресійна форма моделі з геометричним розподілом

лагів така:

1tttt

YXY





   , (8.63)

а для лагів Паскаля з  2r маємо

0111122tttttt

YXXYY

 

     . (8.64)

Методи оцінювання залежать від стохастичної специфікації збурень. Якщо

виконуються класичні умови, то оцінки методу найменших квадратів будуть

спроможними, хоча і зміщеними.

Складнішою буде ситуація у випадку автокорельованих збурень (тут буде доречним

нагадати про некоректність використання критерію Дурбіна –Уотсона для перевірки

автокорельованості збурень у випадку наявності лагових значень залежної змінної).

У численних джерелах можна зустріти твердження про неспроможність оцінок методу

найменших квадратів за умов наявності лагових значень залежної змінної й

автокорельованих збурень. Однак це твердження може виявитись хибним. Для уточнення

можна навести приклад структури автокореляції збурень у моделі (8.63), при якій



виявляється некорельованим з



. У такому випадку коректно застосувати звичайний

метод найменших квадратів з використанням оцінки Неві – Веста для коваріаційної

матриці оцінок параметрів. В інших випадках, наприклад для AR(1)- або для MA(1)-

збурень у моделі (8.63),



корельований з



. У цій ситуації найбільш простим у

практичній реалізації й одночасно найнадійнішим з погляду теорії є

метод

інструментальних змінних