Черняк О.І. та ін. Економетрика

Подождите немного. Документ загружается.

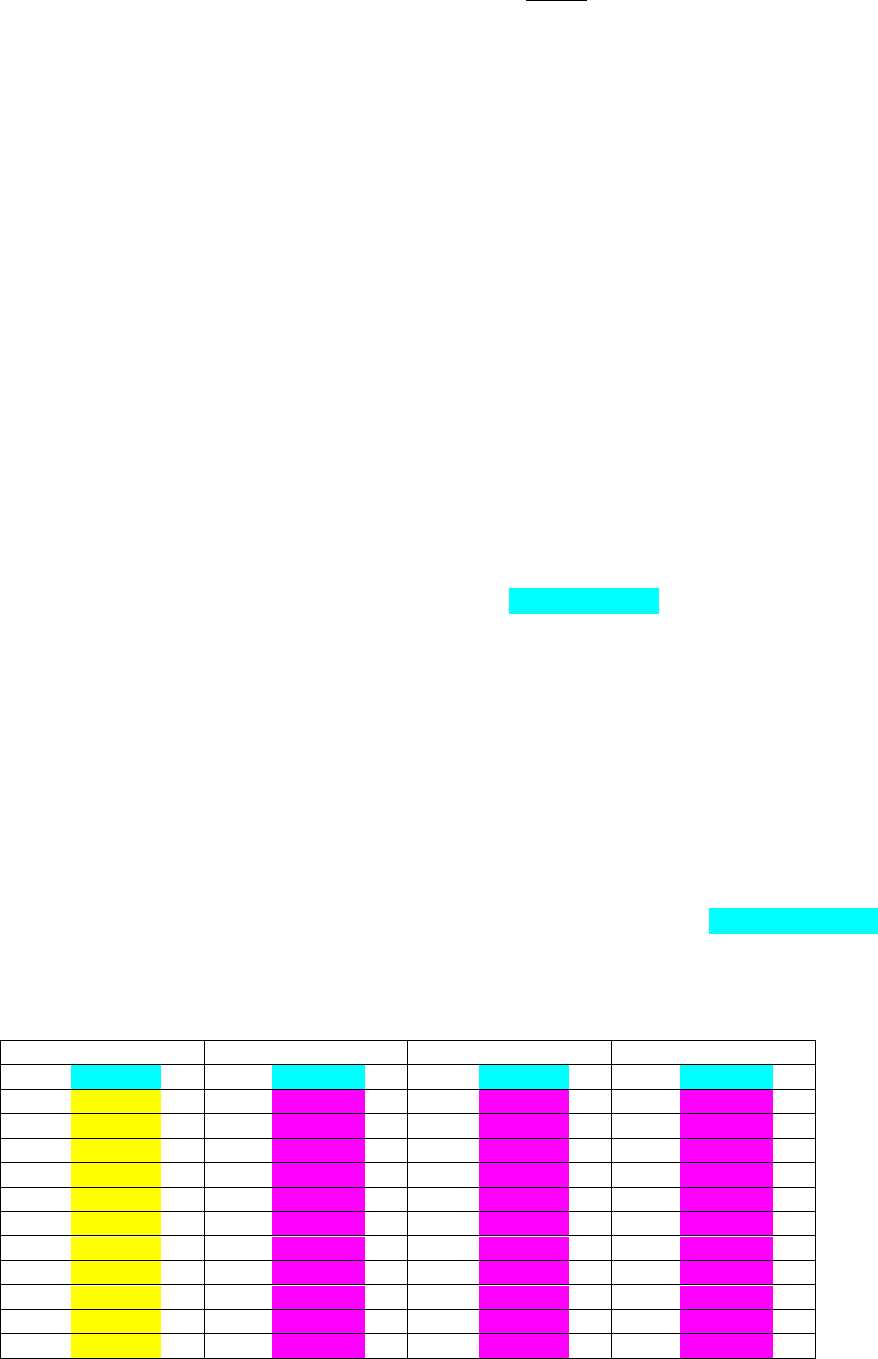
197

Тепер

:0H  (випадкове блукання із дрейфом),

:0H  (лінійний тренд плюс

стаціонарна авторегресія першого порядку).

Статистика критерію становить

()









Правило ухвалення рішення зберігається й у цій ситуації.

За рівності решти умов критичні значення



-статистики в регресії (7.46) ще більше

зміщені ліворуч.

Як ми знаємо, загальний процес реалістично описує стаціонарний часовий ряд. Звідси

випливає, що в більшій частині практичних ситуації збурення в регресіях Дікі – Фуллера

будуть автокорельованими, а отже, критичні значення



-статистик будуть некоректними.

У двох наступних підрозділах буде розглянуто два поширені узагальнення критерію

Дікі – Фуллера, які було розроблено на основі підходів, які узагальнюють два популярні

методи розв'язання проблеми автокореляції в звичайних моделях регресії.

Узагальнений критерій Дікі – Фуллера (критерій Сейда – Дікі). Узагальнений

критерій Дікі – Фулера (Augemented Dickey – Fuller test) у деяких джерелах називають

також критерієм Сейда – Дікі. Замість моделей (7.44)–(7.46) в аналогічних ситуаціях

розглядають такі регресії:

11 1tt t ptpt

yy y y

 

    , (7.47)

11 1

tt t ptpt

yy y y

 

    (7.48)

11 1tttptpt

yty y y

 



        . (7.49)

Довжину лага p вибирають таким чином, щоб позбутися автокореляції збурень. На

практиці довжину лага рекомендовано вибирати, мінімізуючи значення критерію

Шварца, або Ханнана – Квіна. Формулювання гіпотез, статистики критеріїв і алгоритми

перевірки будуть такими самими, як у моделях (7.44)-(7.46). Граничний розподіл також

виражено як функціонал від стандартного вінерівського процесу. Доведено, що розподіл

статистик критеріїв не залежить від довжини лага p.

Критерій Філіпса – Перрона. Цей критерій ґрунтується на моделях (7.44)-(7.46),

однак, статистики коригують на основі оцінки коваріаційної матриці, коректної в умовах

автокореляції.

Якщо ряд має одиничний корінь, треба дослідити перші різниці ряду. За необхідності

процедуру слід продовжити, аж поки ми не одержимо стаціонарний процес. Таким чином

ми, урешті-решт, відшукаємо порядок інтегрованості ряду.

Приклад 7.2. Оцінювання ARIMA-процесу

Виберемо найкращу

RIMA

–модель для часового ряду ВВП України за 1996-2007 рр.,

поданого в таблиці (оскільки вихідні дані мають експоненційний тренд та яскраво

виражену сезонність, то значення ВВП попередньо логарифмовані й сезонно

скориговані). Треба оцінити цю модель.

Логарифм натуральний номінального ВВП України (млн грн). Дані сезонно

скориговано.

(???)

Квартал Ln(ВВП) Квартал Ln(ВВП)

1996/Q1 9,880484 2002/Q1 10,87420

1996/Q2 9,871042 2002/Q2 10,88733

1996/Q3 9,903196 2002/Q3 10,94175

1996/Q4 9,984332 2002/Q4 10,99981

1997/Q1 9,997500 2003/Q1 11,02986

1997/Q2 10,00711 2003/Q2 11,06915

1997/Q3 10,04604 2003/Q3 11,09409

1997/Q4 10,12640 2003/Q4 11,14147

1998/Q1 10,10917 2004/Q1 11,24870

1998/Q2 10,13560 2004/Q2 11,34189

1998/Q3 10,14310 2004/Q3 11,37937

1998/Q4 10,17939 2004/Q4 11,41734

198

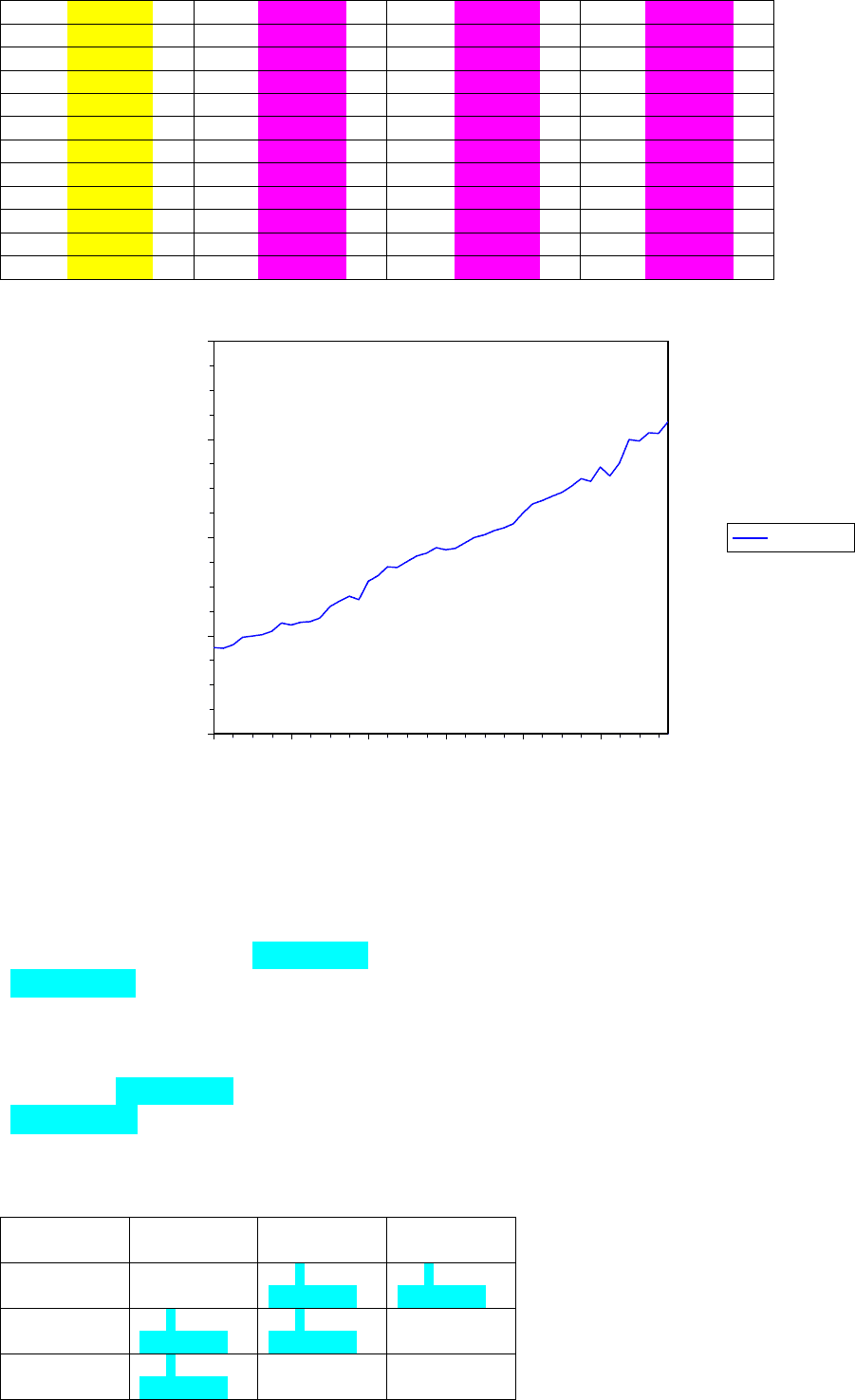
1999/Q1 10,29410 2005/Q1 11,46207

1999/Q2 10,35426 2005/Q2 11,52510

1999/Q3 10,39990 2005/Q3 11,60069

1999/Q4 10,36714 2005/Q4 11,57479

2000/Q1 10,55590 2006/Q1 11,71521

2000/Q2 10,61096 2006/Q2 11,62674

2000/Q3 10,70382 2006/Q3 11,75759

2000/Q4 10,69032 2006/Q4 11,99425

2001/Q1 10,75327 2007/Q1 11,98195

2001/Q2 10,81275 2007/Q2 12,06783

2001/Q3 10,84276 2007/Q3 12,06184

2001/Q4 10,89231 2007/Q4 12,17469

1996 1998 2000 2002 2004 2006

ln(ВВП)

Рис. 7.1. Логарифм натуральний сезонно скоригованого квартального ВВП України за 1996–

2007 рр.

Розв'язання. Спочатку визначимо тип процесу. Оскільки графік даних (рис. 7.1)

показує, що дані приблизно мають лінійний тренд, застосуємо узагальнений критерій

Дікі – Фуллера, що ґрунтується на регресії (7.49). Мінімізуючи значення критерію Шварца,

вибираємо довжину лага в регресії Дікі – Фуллера рівною нулю. Вибіркове значення



статистики становить 2,844175 , що перевищує десятивідсоткове критичне значення



(

3,184230

)

. Отже, ми не можемо відхилити гіпотезу про наявність одиничного кореня.

Різниці ряду не мають явного тренда, а їхнє середнє значення значущо відрізняється від

нуля. Тому до різниць застосовуємо варіант критерію з регресією (7.49). Довжина лага,

обрана на основі критерію Шварца, дорівнює нулю. Вибіркове значення

 -статистики

дорівнює 8,954576 , тобто є меншим, ніж одновідсоткове критичне значення



(

3,581152

)

. Це вказує на стаціонарність різниць. Таким чином, робимо висновок, що ряд

є інтегрованим першого порядку.

Тепер слід вибрати

(

)

ARMA p q -модель для різниць. Вибиратимемо, мінімізуючи

критерій Шварца для моделей, у яких 2pq



 :

0 1 2

0 –

2,813744

–

2,723430

1 –

2,833687

–

2,753423

2 –

2,751957

199

Найменше значення 

(

2,833687

)

SIC дає модель

(

0,1

)(

)

RMA MA , яку ми й

обираємо. Усі значення Q -статистики для

220k



 значно менші за відповідні критичні

значення. Отже, робимо висновок про некорельованість залишків моделі. Оцінена модель

для різниць є такою:



  

ˆˆ

0,049 0, 357

ttt

Відповідно, вихідний ряд можна описати таким процесом

(

0,1,1

)

ARIMA :





ˆˆ

0,049 0,357

tttt

yy .

Обчислення здійснено в програмному середовищі EViews 5.1.

7.13. Регресія у випадку тренд-стаціонарних часових рядів

Нехай залежна змінна

є тренд-стаціонарною з лінійним трендом, тобто

yt  , (7.50)

де

 – стаціонарний випадковий процес із нульовим середнім.

Наша мета – дослідити лінійну залежність між

та набором змінних



 

,1 , 1

(

1, , ,

)

tt tk

xxx . Якщо змінні були б стаціонарними, ми почали б з оцінювання моделі

множинної регресії



tt t

y x β

(7.51)

де



 

(,, )

β ,

 – збурення (можливо, автокорельовані). Уведемо також таке

позначення:

-0 

 

(, , )

β , тобто

-0

β – вектор коефіцієнтів при всіх незалежних

змінних, окрім константи.

Спочатку проаналізуємо властивості цієї моделі в наявних умовах. Якщо у тренд-

стаціонарний, а всі елементи

– стаціонарні, то модель (7.51) апріорі некоректна,

оскільки збурення в цій моделі не можуть бути стаціонарними. У тому випадку, коли

принаймні один із набору регресорів

є тренд-стаціонарним, за відсутності залежності

між змінними

R у моделі (7.51) прямує до одиниці зі швидкістю







(тобто

1 R







), якщо

 є білим шумом, і зі швидкістю







, якщо

 є випадковим

блуканням. Тому коефіцієнт детермінації в цих умовах не є інформативним. Оцінки

коефіцієнтів β зміщені та неспроможні (окрім ситуації, яку буде розглянуто нижче).

Таким чином, звичайна регресія, тобто модель (7.51), буде некоректною.

Виявляється, що зміни, які слід внести до моделі (7.51), не такі вже й значні. Слід

обов'язково включити відповідний тренд до рівняння



 

tt t

ytx β

(7.52)

Модель (7.52) оцінюють, виходячи із властивостей збурень, так само, як у випадку

стаціонарних змінних. Однак ця модель має певні особливості. Насамперед оскільки

завжди прямує до одиниці, то стандартна F-статистика для перевірки гіпотези про

значущість прямує до нескінченності. Отже, її використовувати не можна. Натомість

звичні t- та F-статистики для перевірок гіпотез про обмеження на β та  (окрім

-0



0β

та

0 одночасно, тобто крім стандартного формулювання гіпотези про значущість) будуть

коректними. Стандартне формулювання гіпотези про значущість моделі (7.52) замінює

гіпотеза

-0

 0β

Рекомендуємо такий алгоритм. Слід оцінити моделі (7.50) і (7.52). Основою аналізу є

модель (7.52). Слід окремо перевірити гіпотези

-0



0β та





. Залежно від результатів

перевірок варто розрізняти такі випадки:

200



-0

 0β та

0

. Регресори пояснюють як тренд залежної змінної, так і

короткострокові відхилення від тренда. У цій ситуації модель (7.51) коректна і слід

перейти до неї (пам'ятайте про зауваження стосовно коефіцієнта детермінації).



-0

 0β

та 0 . У цьому випадку слід порівняти коефіцієнти при тренді в моделях

(7.50) і (7.52).

Формальну перевірку рівності здійснюють за допомогою такої штучної моделі. Маємо

2n спостережень:

 (, ,, )

yyyy





(

,,0,,0

)

,1,1

1, ,

xx jk

jjnj

Замість константи з’являються дві фіктивні змінні. В одній n перших координат –

одиниці, а n останніх – нулі, у другій – навпаки. Замість тренда маємо дві такі змінні:





(0, ,0,1,2, , )

та





(1,2,,,0,,0)

Цю модель слід оцінювати методом зважених найменших квадратів з вагами,

пропорційними до стандартних відхилень збурень у моделях (7.50) і (7.52). Гіпотеза про

рівність коефіцієнтів при двох останніх змінних в описаній моделі еквівалентна гіпотезі

про рівність коефіцієнтів при тренді в моделях (7.50) і (7.52). Якщо коефіцієнти значно не

відрізняються, то

це означає, що х-и здатні пояснювати лише короткострокові відхилення

у від тренда, джерело якого лишається нез'ясованим. Якщо коефіцієнти відмінні, то це

означає, що х-и частково пояснюють тренд у, однак, частина джерел тренда в явному

вигляді невідома. У цій ситуації треба залишити модель (7.52).

Основні факти такі. Модель здатна коректно

оцінювати вплив незалежних змінних, її

можна використовувати для прогнозування. Однак довгострокову поведінку у (частково

або повністю) не можна пояснити, а лише формально змоделювати за допомогою тренда.

Щоб охарактеризувати вплив незалежних, рекомендуємо обчислити частковий коефіцієнт

детермінації. Для цього треба спочатку оцінити моделі тренда для у і для кожного х. Потім

слід

оцінити регресію залишків у стосовно залишків кожного з х-ів. Звичайний R

останній регресії є частковим коефіцієнтом детермінації у вихідній моделі. Проте

останній має лише обмежену цінність, оскільки показує, наскільки х-и пояснюють

відхилення залежної змінної від власного тренда. Для виявлення того, наскільки х-и

пояснюють тренд у, пропонуємо псевдо-коефіцієнт детермінації, який треба обчислювати

таким чином. Позначимо через

β та



оцінки коефіцієнтів β та  у моделі (7.52).

Оцінимо регресію   

tx β . Нехай



– оцінка



. Тоді









Pseudo

R .

Пропонований коефіцієнт ґрунтується на методології арифметики зростання Солоу.

Задачі

Група А

Задача 7.1.

Знайдіть автокореляційну функцію такого

(

)

MA -процесу:

0,7 0,2

tt t t





    .

Задача 7.2. Знайдіть автокореляційну функцію такого

(

)

R -процесу:

0,7( )

ttt



   .

Побудуйте графік



у діапазоні 66k  .

Задача 7.3. Покажіть, що значення автокореляційної функції

(

1,1

)

ARMA -моделі

11tttt



   можна обчислювати за такою формулою:

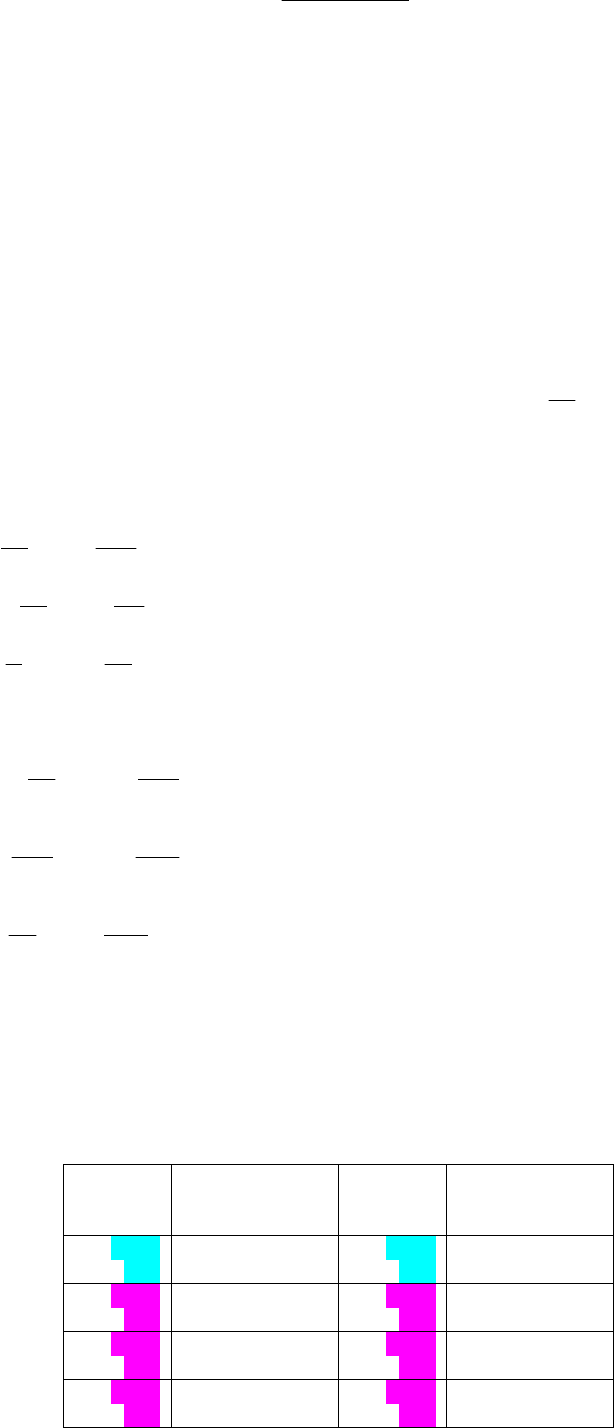
201

()(1)

, 1,



 







  













Задача 7.4. Запишіть кожну з наведених нижче моделей за допомогою полінома від

оператора лага. Визначте, чи є вони стаціонарними та/або оборотними:

а)

0,3

ttt



;

б)

1, 3 0, 4

tt t t



    

;

в)

112

0,5 1,3 0, 4

tttt t



;

г)

12 12

0,03 0, 7 0, 9 0,2 0,5

tttttt

yyy

 

  

Для моделі (а) знайдіть еквівалентне

-зображення.

Задача 7.5. Покажіть, що

(

)

AR -процес вигляду

12tt t t

yy cy





 є стаціонарним

при 10c  . Знайдіть автокореляційну функцію при

c  . Покажіть, що

(

)

AR -

процес

123tt t t t

yy cy cy

 



– нестаціонарний для будь-якого значення c .

Задача 7.6. Знайдіть параметри моделі

(

)

AR , якщо:

а)

13 113

1, ,

14 140

     ;

б)

11 41

2, ,

13 65

     ;

в)

113

3, ,

715

    

Задача 7.7. Знайдіть параметри моделі

(

1,1

)

ARMA , якщо:

а).

13 91

4, ,

19 190

    

;

б).

11 11

3, ,

175 350

    

;

в).

31 93

1, ,

41 205

    

Група Б

Задача 7.8.

Оберіть найкращу

RIMA -модель для часового ряду ВВП України за

1999-2007 рр., поданого в таблиці. Оцініть обрану модель. На основі даних за 1999-

2006 рр. розрахуйте прогноз на 2007 р. Визначте похибку прогнозування.

(???)

Пері

од

ВВП

України,

млн грн

Пері

од

ВВП

України,

млн грн

1996

/01 5060

2002

/01

14128

1996

/02 5140

2002

/02

13412

1996

/03 6488

2002

/03

16592

1996

/04 5062

2002

/04

14412

202

1996

/05 5730

2002

/05

17080

1996

/06 7075

2002

/06

18625

1996

/07 5155

2002

/07

18569

1996

/08 6740

2002

/08

23474

1996

/09 10615

2002

/09

23024

1996

/10 4810

2002

/10

14720

1996

/11 7529

2002

/11

18623

1996

/12 12115

2002

/12

33151

1997

/01 5920

2003

/01

15021

1997

/02 6107

2003

/02

15562

1997

/03 6701

2003

/03

20952

1997

/04 7493

2003

/04

15714

1997

/05 6998

2003

/05

18509

1997

/06 5994

2003

/06

25741

1997

/07 8383

2003

/07

14143

1997

/08 7503

2003

/08

25481

1997

/09 10190

2003

/09

35957

1997

/10 6584

2003

/10

14604

1997

/11 8205

2003

/11

24654

1997

/12 13287

2003

/12

37827

1998

/01 6544

2004

/01

19099

1998

/02 6511

2004

/02

19231

1998

/03 7816

2004

/03

25785

1998

/04 7189

2004

/04

22530

1998

/05 7640

2004

/05

23225

1998

/06 8538

2004

/06

32834

1998

/07 8262

2004

/07

26416

1998

/08 8594

2004

/08

33282

1998

/09 12052

2004

/09

40306

1998

/10 7701

2004

/10

23740

1998 9905

2004 31341

203

/11 /11

1998

/12 11841

2004

/12

47324

1999

/01 8017

2005

/01

24278

1999

/02 7960

2005

/02

25786

1999

/03 9003

2005

/03

29292

1999

/04 9318

2005

/04

30781

1999

/05 10043

2005

/05

30464

1999

/06 9835

2005

/06

32881

1999

/07 12173

2005

/07

40452

1999

/08 11980

2005

/08

38628

1999

/09 13480

2005

/09

45022

1999

/10 11844

2005

/10

30066

1999

/11 12851

2005

/11

35513

1999

/12 10622

2005

/12

61578

2000

/01 9934

2006

/01

29844

2000

/02 10887

2006

/02

30626

2000

/03 11488

2006

/03

41557

2000

/04 12857

2006

/04

26684

2000

/05 12705

2006

/05

37876

2000

/06 12327

2006

/06

39512

2000

/07 17243

2006

/07

47616

2000

/08 16564

2006

/08

47050

2000

/09 17431

2006

/09

49793

2000

/10 15948

2006

/10

50069

2000

/11 16662

2006

/11

52312

2000

/12 16024

2006

/12

82921

2001

/01 13616

2007

/01

44108

2001

/02 13720

2007

/02

43284

2001

/03 11865

2007

/03

45716

2001

/04 19383

2007

/04

47509

2001

/05 16104

2007

/05

51892

204

2001

/06 10994

2007

/06

61987

2001

/07 25543

2007

/07

59656

2001

/08 21388

2007

/08

65370

2001

/09 12068

2007

/09

70598

2001

/10 25746

2007

/10

70992

2001

/11 18121

2007

/11

68907

2001

/12 15642

205

Розділ 8. Моделі з лаговими змінними

8.1. Приклади з економічної теорії

Досить часто в реальних ситуаціях вплив більшої частини факторів не можна відчути

миттєво. Час, потрібний для того, щоб дія фактора реалізувалася повністю, залежить від

характеристик і міри складності явища, яке аналізують. Розглянемо кілька економічних

прикладів.

Приклад 8.1. Функція споживання

Найпростіша лінійна функція споживання має вигляд

00ttt



  , (8.1)

де

– особисте споживання;

– особистий дохід у розпорядженні;



– збурення;





–

параметри

0 ,

01  .

Частка

CY – це "середня схильність до споживання", а перша похідна



 є

граничної схильністю до споживання.

З рівняння (8.1) випливає, що поточне значення споживання залежить лише від

поточного значення доходу та не залежить від поточних значень будь-яких інших

змінних.

Однак така специфікація моделі може бути некоректною. Наприклад, поточне

споживання може також залежати від поточного рівня нагромаджень. У цьому разі

функція споживання

набуде такого вигляду:

00 0tttt

CYS



   , (8.2)

де

S – особисті нагромадження;

 – параметр моделі.

Розв'язання. Як відомо з економічної теорії, поточний рівень нагромаджень залежить

від доходу попередніх років. Тому функцію нагромаджень можна записати таким чином:

01122

...

tttt

SYYu



    

, (8.3)

де

 (для j = 0,1,...) – параметри моделі;

u – збурення.

Підставимо (8.3) до (8.2) та одержимо



       

000 0 011022 0

()

...

()

tttttt

CYYYu

або

01122

... .

ttttt

CYYY



    (8.4)

З рівняння (8.4) випливає, що поточний рівень споживання залежить від поточного та

минулих значень доходу.

Якщо взяти до уваги так звану постійність звичок, то поточний рівень споживання

залежить від минулих рівнів споживання:

  



      

01122 1122

... ... .

tttt ttt

CYYYCC (8.5)

Приклад 8.2. Акселераторна модель інвестицій

У найпростішій акселераторній моделі інвестицій визначено, що існує зв'язок між

чистими інвестиціями і зміною випуску. Це взаємовідношення можна записати у вигляді

0ttt



, (8.6)

де

– чисті інвестиції;

1ttt

XQQ





;

– випуск;



– параметр.

З моделі випливає, що рівень інвестицій буде значно коливатися. Інвестиції будуть

додатними, якщо економіка у стані піднесення (



 ), і від'ємними, якщо

економіка на спаді (



 ). Однак зміна рівня інвестицій залежить і від інших

факторів, наприклад від розподілу в часі інвестиційних рішень.

Оскільки інвестиційні рішення з різних причин можуть бути відкладені, то реакція

інвестицій на зміну випуску розподіляється в часі. У цьому випадку рівняння (8.6) можна

записати таким чином:

206

0112 2

... .

tttktkt

IXXX

 

    

(8.7)

Приклад 8.3. Кількісна теорія грошей

Кількісна теорія грошей стверджує, що рівень цін в економіці пропорційний обсягу

грошової маси в цій економіці. Це твердження випливає з рівняння І. Фішера

tt t t

MV PQ



, (8.8)

де

M – номінальний обсяг грошової маси;

V – швидкість обігу грошей;

Q – реальний

випуск (обсяг кінцевих товарів і послуг);

P – загальний рівень цін.

Розв'язання. Логарифмуємо співвідношення (8.8):

ln ln ln ln .

ttt t

MV PQ (8.9)

У результаті диференціювання (8.9) за часом одержимо

tt t t

mv pq



, (8.10)

де

dt M dt

. Аналогічно визначаємо

,,.

ttt



У випадку дискретного часу замість похідних розглянемо відносні прирости:

1tt



Перепишемо (8.10) у такому вигляді:

tttt

pmqv





(8.11)

Таким чином, інфляцію визначаємо за зміною реального випуску, зміною номінальної

грошової маси і зміною швидкості обігу грошей.

Монетаристи стверджують, що основним фактором, який визначає інфляцію, є зміна

грошової маси, уважаючи два інші фактори неважливими. Залежно від того, буде

сумарний ефект змін випуску і швидкості обігу позитивним, нульовим чи додатним

інфляція

буде більшою, рівною або меншою, ніж зміна грошової маси.

Отже, з монетаристської позиції, залежність інфляції від обсягу грошей буде такою:

0ttt



 . (8.12)

Тоді як із рівняння (8.12) випливає, що зміна грошової маси діє на інфляцію миттєво, у

реальності реакція інфляції розподілена в часу. Тому залежність (8.12) слід записати у

вигляді



     

01122

... .

ttttt

pmmm

(8.13)

Приклад 8.4. Крива Філіпса

Крива Філіпса в первісному вигляді описує емпіричне співвідношення між відносною

зміною заробітної плати і безробіттям у відсотках до загальної кількості робочої сили. Чим

вище рівень безробіття, тим менше зміна заробітної плати.

Це співвідношення можна записати таким чином:

wUe









, (8.14)

де

()/

ttt t

www w







;

w – рівень заробітної плати;

U – рівень безробіття у відсотках;



– збурення;  0, 0 – параметри.

Припустимо, що заробітна плата залежить також від цін у минулому. Крім того,

зважимо на те, що реакція заробітної плати не є миттєвою. Тоді замість (8.14) слід

записати

... ... ... ,

ttm

wUU ppe











(8.15)

де

()/

ttt t

ppp p







;

– загальний рівень цін; ,



 – параметри.

У всіх розглянутих прикладах значення залежної змінної визначають значення

незалежних змінних у поточний момент часу (миттєва реакція), але й значення за минулі

моменти часу (неперервна, або динамічна реакція). Різниця між поточними та минулими

моментами часу називається часовим лагом або просто лагом, а відповідна змінна

називається

лаговою змінною.