Черняк О.І. та ін. Економетрика

Подождите немного. Документ загружается.

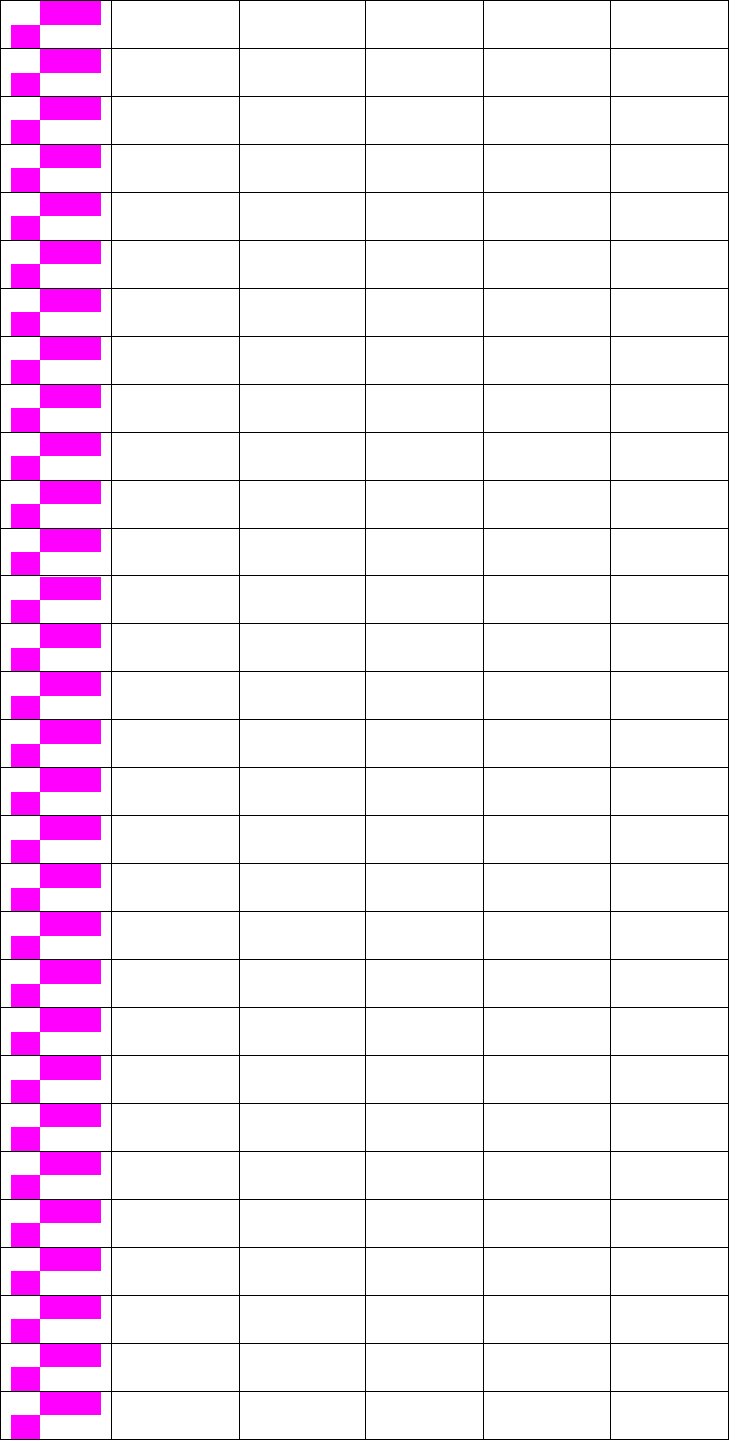
257

1972/

4,5766

3,9005

6,415

854

3,7483

8,035

829

1972/

4,9333

3,7182

6,427

247

4,2413

8,047

446

1972/

5,3333

6,3320

6,435

745

4,8513

8,063

220

1973/

6,2833

5,1878

6,442

297

5,6396

8,087

425

1973/

7,4666

7,3710

6,435

847

6,6083

8,091

811

1973/

9,8733

7,5045

6,428

663

8,3883

8,090

801

1973/

8,98 9,3811

6,417

550

7,4616

8,098

369

1974/

8,3033

6,3878

6,418

051

7,6003

8,089

298

1974/

10,456

667

8,2983

6,406

561

8,268 8,091

811

1974/

11,533

333

11,891

6,385

880

8,2863

8,083

051

1974/

9,05 9,6535

6,373

887

7,336 8,079

122

1975/

6,5633

11,410

6,351

073

5,8733

8,056

427

1975/

5,92 5,4572

6,352

346

5,4006

8,067

902

1975/

6,6666

8,3506

6,350

277

6,3366

8,086

380

1975/

6,12 6,7269

6,341

396

5,6843

8,099

402

1976/

5,29 5,1718

6,341

862

4,9533

8,118

714

1976/

5,57 5,1180

6,345

223

5,1686

8,122

431

1976/

5,53 6,2017

6,340

273

5,1686

8,125

927

1976/

4,99 6,8614

6,342

037

4,6983

8,136

313

1977/

4,81 5,4079

6,351

912

4,624 8,150

872

1977/

5,2366

8,1503

6,349

046

4,8286

8,167

636

1977/

5,8066

6,9745

6,348

404

5,472 8,181

553

1977/

6,5933

7,0500

6,351

865

6,137 8,179

536

1978/

6,7966

5,6438

6,357

512

6,408 8,186

409

1978/

7,2 10,370

6,353

586

6,481 8,217

978

1978/

8,0833

7,7627

6,353

993

7,3153

8,225

664

1978/

9,8966

8,6832

6,349

470

8,6803

8,237

373

1979/

10,096

667

7,8207

6,342

107

9,3576

8,237

691

1979/

9,8533

8,5493

6,345

397

9,3723

8,238

616

1979/

10,603

333

8,8086

6,347

885

9,6313

8,244

728

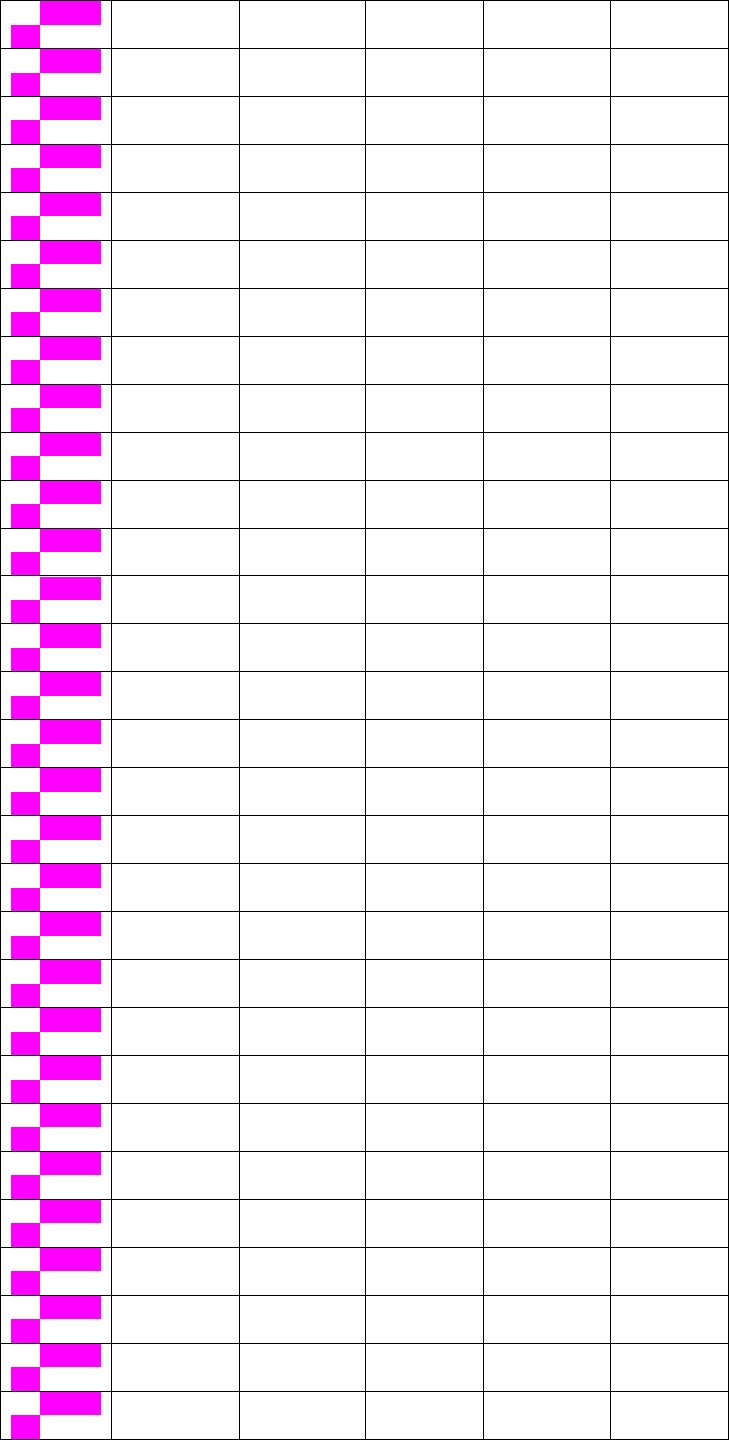
258

1979/

13,096

667

7,9574

6,336

670

11,803

667

8,246

591

1980/

14,253

333

9,2141

6,330

169

13,458

667

8,250

829

1980/

10,75 9,4505

6,298

007

10,049

333

8,224

860

1980/

9,6466

9,0866

6,312

097

9,2353

8,225

101

1980/

14,513

333

10,479

6,312

904

13,709

667

8,244

991

1981/

14,52 11,251

6,296

084

14,369 8,258

552

1981/

15,35 6,9857

6,302

509

14,829 8,254

373

1981/

16,213

333

9,3234

6,284

129

15,087

333

8,259

588

1981/

12,94 8,5695

6,275

268

12,022

667

8,243

572

1982/

13,696

667

4,5346

6,286

486

12,895 8,231

136

1982/

13,483

333

5,2402

6,282

984

12,359 8,235

122

1982/

11,553

333

4,0572

6,285

005

9,7053

8,230

684

1982/

8,81 3,3336

6,316

703

7,935 8,232

068

1983/

8,34 4,8824

6,332

228

8,0813

8,238

405

1983/

8,6066

2,8123

6,355

529

8,419 8,265

264

1983/

9,44 3,9181

6,368

987

9,1866

8,280

052

1983/

9,19 4,2134

6,375

867

8,7933

8,297

070

1984/

9,45 5,6207

6,377

857

9,1333

8,316

178

1984/

10,773

333

4,1585

6,384

305

9,8433

8,329

417

1984/

11,146

667

4,5626

6,382

478

10,343

333

8,334

808

1984/

9,2566

2,6370

6,386

530

8,9733

8,341

458

1985/

8,69 4,6399

6,400

523

8,1833

8,348

017

1985/

7,91 2,6809

6,418

486

7,5233

8,355

803

1985/

7,7233

2,8038

6,446

560

7,1033

8,368

461

1985/

7,7 3,9239

6,464

576

7,1466

8,374

131

1986/

7,4133

1,9726

6,480

989

6,8866

8,387

198

1986/

6,5433

1,7987

6,515

254

6,13 8,386

560

1986/

5,8933

3,1998

6,549

046

5,5333

8,392

219

1986/

5,7266

2,9906

6,584

086

5,34 8,395

500

1987/

5,95 3,5977

6,606

894

5,5333

8,402

904

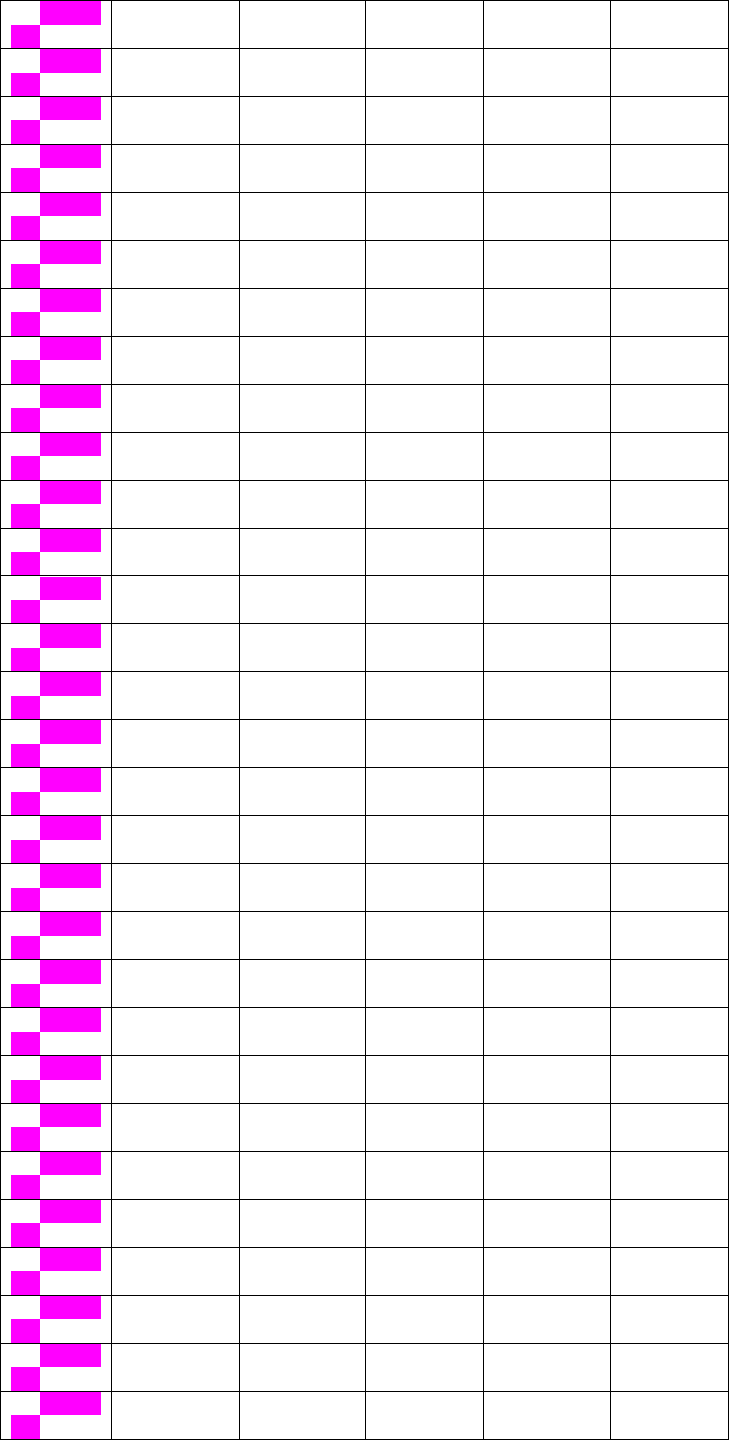
259

1987/

6,8466

2,8525

6,617

196

5,7333

8,415

227

1987/

7,0266

3,0551

6,611

214

6,0333

8,424

924

1987/

7,54 3,6979

6,612

419

6,0033

8,439

340

1988/

6,7133

3,3155

6,611

622

5,76 8,445

762

1988/

7,2533

4,4941

6,618

918

6,23 8,456

339

1988/

8,1633

4,8347

6,619

848

6,9933

8,462

631

1988/

8,5866

3,9898

6,612

931

7,7033

8,472

133

1989/

9,4466

5,1121

6,598

751

8,5333

8,480

031

1989/

9,29 4,3546

6,577

275

8,44 8,484

463

1989/

8,39 3,7608

6,572

754

7,85 8,484

463

1989/

8,0566

3,5021

6,576

606

7,6333

8,488

114

1990/

8,0766

5,2574

6,574

452

7,7566

8,496

643

1990/

8,1933

4,2118

6,574

546

7,7666

8,500

474

1990/

7,8333

3,9482

6,575

841

7,4933

8,498

316

1990/

7,68 4,2256

6,573

205

7,0233

8,490

274

1991/

6,5966

4,8463

6,574

205

6,0533

8,485

083

1991/

6,0566

2,7397

6,587

026

5,5933

8,490

418

1991/

5,83 2,7829

6,599

436

5,4066

8,492

880

1991/

4,9166

2,4668

6,617

347

4,5833

8,493

064

1992/

4,19 3,7775

6,648

784

3,91 8,500

759

1992/

4,03 2,6704

6,668

766

3,7233

8,506

638

1992/

3,41 1,3525

6,692

511

3,13 8,515

291

1992/

3,5666

2,6467

6,724

760

3,0766

8,529

260

1993/

3,2866

3,1426

6,737

378

2,9933

8,532

141

1993/

3,2566

1,7190

6,759

368

2,9833

8,538

054

1993/

3,31 1,0925

6,786

213

3,02 8,544

692

1993/

3,3666

1,3387

6,806

020

3,08 8,559

869

1994/

3,6666

2,6302

6,814

227

3,25 8,568

095

1994/

4,7266

2,9385

6,811

526

4,0366

8,578

119

1994/

5,2133

2,0787

6,813

823

4,51 8,588

024

260

1994/

6,11 1,2178

6,807

213

5,2833

8,600

394

261

Розділ 11. Моделі з обмеженими залежними змінними і моделі з панельними

даними

11.1. Моделі з обмеженими залежними змінними

11.1.1. Моделі бінарного вибору

Припустимо, що нас цікавить, чому певна сім'я має або, навпаки, не має автомобіль.

Нехай єдиною пояснювальною змінною є дохід. Ми зібрали дані про

n сімей





1,in .

Позначимо через

дохід і-ї сім'ї. Визначимо залежну змінну

таким чином:



y  , якщо

-та сім'я має автомобіль;



y 

, якщо i -та сім'я не має автомобіля.

Проаналізуємо модель лінійної регресії

, 1, .

iii

xin   

З одного боку,







M| ,

ii i

оскільки за стандартним припущенням регресії







M| 0.

З іншого боку,



      M | 1 { 1|}0 { 0|} { 1|}.

ii ii i i ii

Отже,

{1|} .

ii i

Py x x



 

Це співвідношення показує, що модель лінійної регресії буде нереалістичною, оскільки

вираз

0 i

x

не обов'язково обмежено нулем та одиницею. Крім того, виникають

проблеми з властивостями збурень. Для розв'язання цієї проблеми було запропоновано

підхід так званих латентних змінних. Припустимо, що справжня модель має вигляд

iii

yx   але значення змінної *

ми не спостерігаємо. Тому змінна *

називається латентною, або прихованою. Значення спостережень

y пов'язані зі

значеннями латентної змінної

таким чином:



y  , якщо 0

y  ;



y 

, якщо

y 

Латентну змінну можна інтерпретувати як "здібність" , "здатність" або "схильність".

Тобто якщо здатність або схильність придбати автомобіль (або, скажімо, в іншій моделі –

повернути кредит) є додатною, то сім'я купує автомобіль (повертає кредит тощо). Інша

можлива інтерпретація – це різниця функції корисності для двох рішень. Параметри

моделі оцінюють методом максимальної правдоподібності. Позначимо

через F функцію

розподілу збурень і припустимо, що розподіл збурень є симетричним. Тоді

 

01 01 01

{1}{ 0}{ 0}

{}{},

ii ii

iiii i

Py Py P x

PxPxFx



   

     



{ 0} { 0} 1 { 0} 1 .

ii i i



  

Таким чином, функція правдоподібності має вигляд











01 01

:1 ; 0

iy iy

LF x F x



     



Поки що ми визначили латентну змінну з точністю до довільної константи. Справді,

визначимо ** *,

 де 0 .

Тоді:

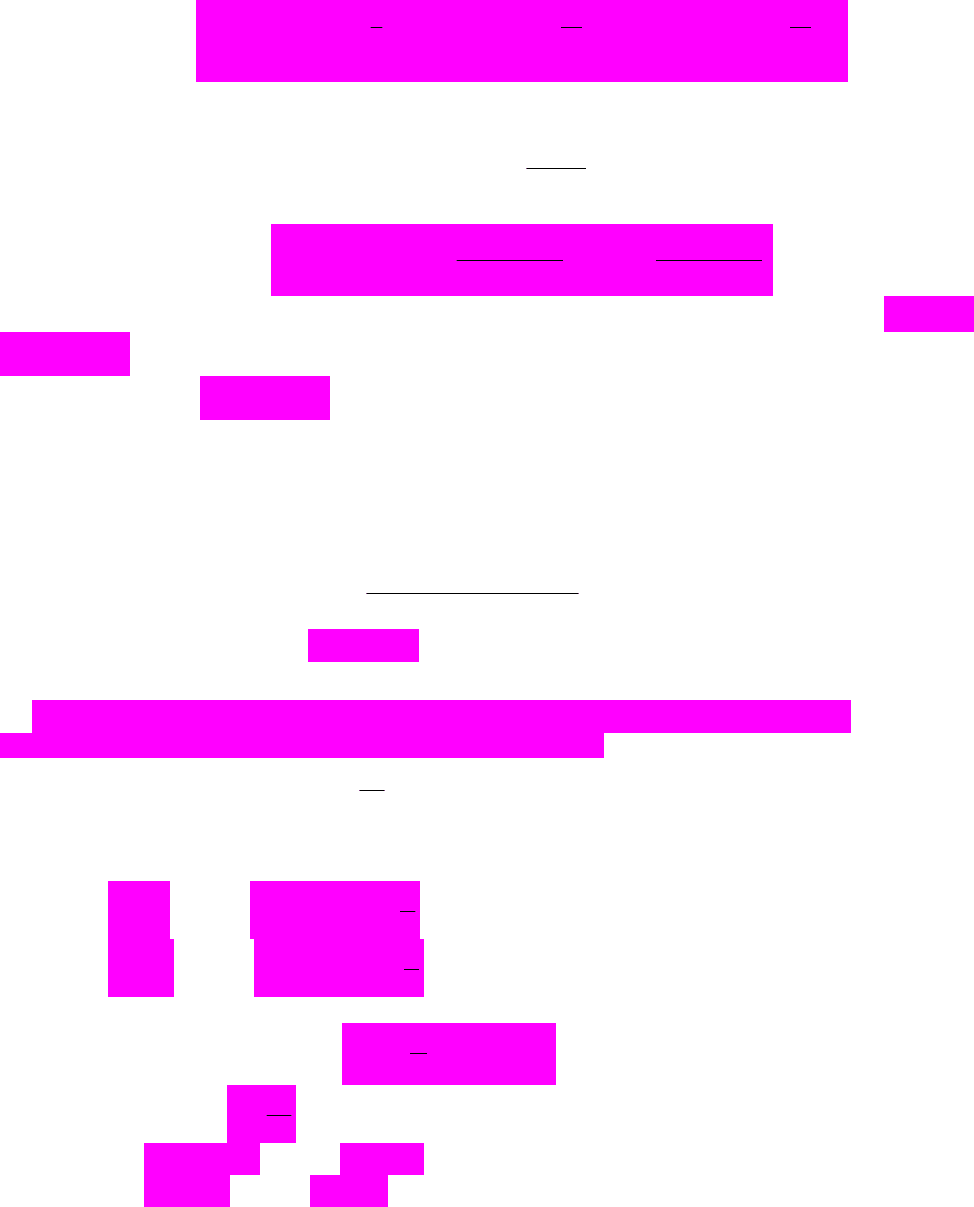
262

 якщо 0,



 то 1

y  ;



якщо 0,



 то 0.

y 

Дисперсії збурень для двох варіантів латентної змінної відрізнятимуться в



разів,

тому ми можемо однозначно визначити латентну змінну, зафіксувавши її дисперсію.

Найчастіше припускають, що збурення мають стандартний нормальний розподіл.

Модель, одержувана в такому випадку, отримала назву

моделі пробіт. Логарифм

функції правдоподібності має вигляд







 



  

   





22 2

:1 :0

ln , 2 ln ln .

nx x

iy iy

Ledxedx

Модель логіт одержують у припущенні, що збурення мають логістичний розподіл з

функцією розподілу







Логарифм функції правдоподібності має вигляд





 



  





01 01

;1 :1

,ln ln .

iy iy

Для обох моделей зручно інтерпретувати не регресійну функцію 

ˆˆ

x , а





ˆˆ

Fx, де F

– відповідна функція розподілу. З виведення функції правдоподібності

видно, що вираз





ˆˆ

Fx є оцінкою ймовірності {1},



тобто оцінкою ймовірності

того, чи сім'я матиме автомобіль, чи буде повернуто кредит тощо. Унаслідок того, що

функції розподілу монотонно зростають, знаки коефіцієнтів інтерпретують майже

звичним способом. Для характеристики згоди моделі використовують кілька варіантів

псевдо

R :

Псевдо

R за Т. Амемійя



1 2 ln ln /

LLn





2) Псевдо

за Д. Мак-Фейденом

1ln /ln ,RLL

де

ln L - значення логарифмічної функції правдоподібності, обчислене при

значеннях аргументів, що дорівнюють ММП-оцінкам;

 

01 1 1

ln ln / ln 1 ;

Ln nn nn









1 i





Псевдо

R , що ґрунтується на коректних прогнозах.

Визначимо прогнози таким чином:

 

y , якщо





 

ˆˆ

;

 

y , якщо



 

ˆˆ

Fx.

Частка некоректних прогнозів дорівнює









wv y y

Позначимо через 

– частку одиниць у вибірці. Визначимо:

 

wv , якщо 

0,5;





, якщо 

0,5 .

Псевдо

R визначаємо таким чином:

263



11.1.2. Моделі з упорядкованим відгуком

Розглянемо вибір між M можливостей, які ми занумеруємо від 1 до M . Якщо ці

можливості можна впорядкувати логічно (наприклад, автомобіля немає, один автомобіль,

більш ніж один автомобіль), то в такій ситуації застосовують так звані моделі з

упорядкованим відгуком. В основу також покладено ідею латентних змінних. Для

випадку єдиної пояснювальної змінної можна записати:

iii

yx  

yj , якщо



 

де

,0, ,

        а решта

 невідомі.

У припущенні, що збурення незалежні і мають стандартний нормальний розподіл,

одержуємо модель пробіт з упорядкованим відгуком, а якщо збурення мають

логістичний розподіл,

одержуємо модель логіт з упорядкованим відгуком. При 2M



маємо звичайні моделі. Розглянемо приклад. Припустимо, що заміжні жінки відповідають

на запитання: "Скільки часу ви бажаєте працювати?", причому анкета опитування

містить три варіанти відповіді: "ні", "неповний робочий тиждень", "повний робочий

тиждень". Згідно з неокласичною теорією відповідь залежить від індивідуальних переваг і

бюджетного обмеження. Такими чинниками можуть бути вік, склад сім'

ї, дохід чоловіка,

рівень освіти тощо. Для простоти розглянемо модель з однією незалежною змінною.

Будемо вважати, що залежна змінна набуває значень таким чином:



y  , якщо відповідь "ні";



y 

, якщо відповідь "неповний робочий тиждень";



y  , якщо відповідь "повний робочий тиждень".

Модель записуємо в такому вигляді:



iii

yx  



y  , якщо *0

y  ;



y  якщо 0*

y;



y  якщо *

y ;



 незалежні і мають стандартний нормальний розподіл.

Латентну змінну можна проінтерпретувати як бажання працювати або як кількість

робочих годин. Таким чином,







{ 1|} { 0|} ,

ii i i i

Py x Py x F x



 







{3|}{ |}1

ii i i i

xF x



















01 01

{2|} ,

ii i i

Py x P x P x

де

F – функція розподілу для стандартного нормального розподілу. Невідомий параметр 

оцінюють методом максимальної правдоподібності разом з



. У результаті

підстановок y попередні формули

замість

x і оцінок замість параметрів одержимо

оцінки ймовірностей кожної можливості, якщо значення пояснювальної змінної дорівнює

x .

11.1.3. Моделі Тобіт

У деяких ситуаціях залежна змінна буде неперервною, але діапазон її значень

обмежений. Досить часто значення залежної змінної дорівнює нулю для значної частини

популяції і є додатним для решти популяції. Як приклади можна назвати витрати на

264

товари тривалого користування, робочі години, обсяги прямих іноземних інвестицій, що

їх зробила фірма.

Уперше модель запропонував Джеймс Тобін у 1958 р., а свою назву – Тобіт – вона

одержала в 1964 р. завдяки Артуру Голдбергу, який підкреслив її подібність до моделей

пробіт. Згодом було запропоновано різноманітні узагальнення цієї моделі. Ми розглянемо

стандартну модель Тобіт, або, як її іноді називають, модель цензурованої регресії:



iii

yx   , 1, ;in



yy , якщо *0;

y 



y  , якщо *0;

y 





незалежні і мають розподіл





0, .N 

Латентну змінну *

зазвичай інтерпретують як "бажану" кількість. Логарифм функції

правдоподібності має вигляд







ln , , ln 1

ln exp ,









   









 

















де F-функція розподілу стандартного нормального розподілу. Звернімо увагу на

особливість інтерпретації регресійних коефіцієнтів і вибіркової регресійної функції.

Очікувані значення залежної змінної знаходять таким чином:





 

  







01 01

ˆˆ ˆˆ

ˆˆ

M| ˆ ,

ˆˆ

yx xF

де F – функція розподілу, а  – щільність стандартного нормального розподілу. Граничний

ефект незалежної змінної не дорівнює регресійному коефіцієнту. За умови цензурування















ˆˆ

Оскільки оцінки параметрів знаходять методом максимальної правдоподібності, то

коваріаційну матрицю визначають і перевірку гіпотез здійснюють у межах звичайної для

ММП схеми.

11.2. Моделі з панельними даними

11.2.1.Переваги панельних даних

Панельні дані, або панель утворюється таким чином. Припустимо, що ми маємо N

одиниць спостереження





1,iN , причому для кожної одиниці (особи, домогосподарства,

фірми, галузі промисловості, країни тощо) ми спостерігаємо набір показників за





1,Tt T періодів часу. Через

y будемо позначати значення залежної змінної для i -ї

одиниці спостереження в момент часу

t . Набір значень k незалежних змінних, не

враховуючи константу, позначимо через

. Лінійну модель можна записати у такому

вигляді:

  

it i it it

y x  ,

де  – вектор параметрів, які характеризують граничний ефект незалежних змінних на

залежну. Це означає, що ефекти від зміни

x однакові для всіх одиниць у всіх

спостереженнях, але середні значення змінних можуть відрізнятись від одиниці до

одиниці спостереження. Отже,



відображає дію факторів, специфічних для конкретної

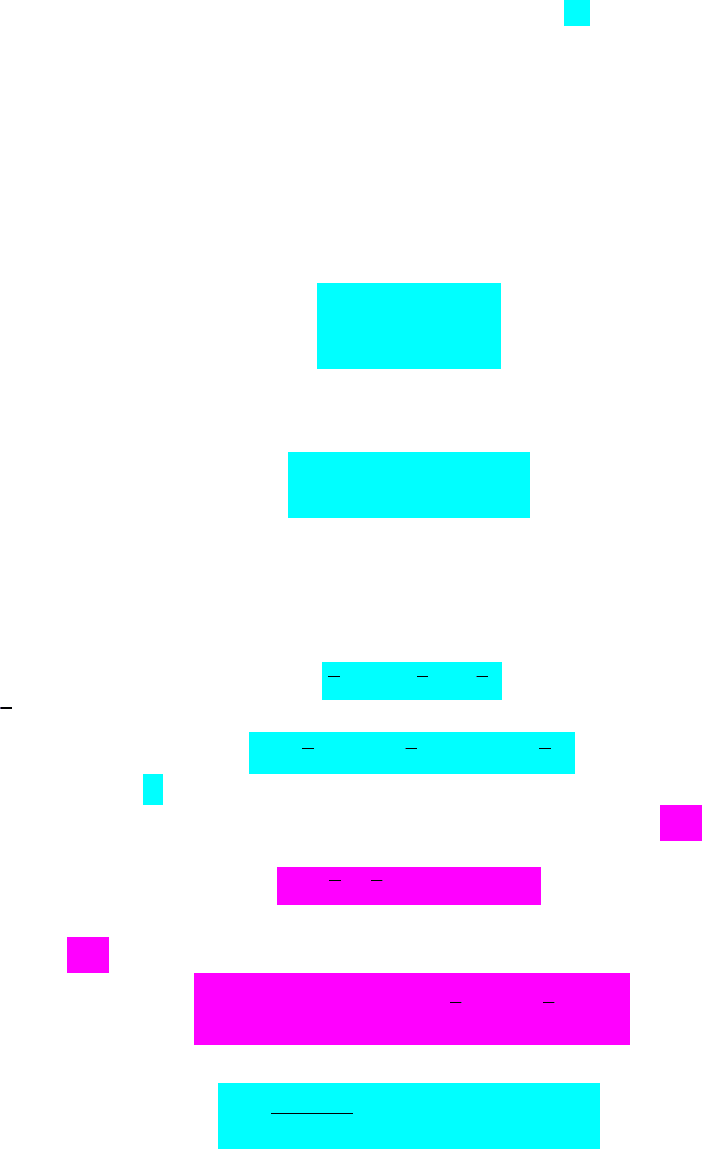
265

одиниці спостереження, але не змінюються з часом. У стандартному випадку

припускають, що

 незалежні й однаково розподілені з нульовим середнім і дисперсією



 . Якщо

 трактують як фіксовані невідомі параметри, то модель називають моделлю з

фіксованими ефектами, а випадок, коли



утворюють вибірку з розподілу із середнім



і дисперсією



 одержав назву моделі з випадковими ефектами. Тут важливим є

припущення, що

 не залежить від

. Моделі з панельними даними дозволяють

аналізувати зміни на індивідуальному рівні. Розглянемо ситуацію, коли середній рівень

споживання зростає на 2 % щорічно. Це може бути викликано тим, що споживання

кожного зростає на 2 %, або, скажімо, тим, що приблизно половина збільшила

споживання на 4 %, а в решти рівень споживання не змінився. Дослідження показали,

що оцінювання за панельними даними найчастіше буде більш ефективним порівняно з

ситуацією, коли доступний такий самий обсяг даних, але дані утворюються в результаті

вибору різних одиниць у кожний період часу. Моделі з панельними даними є більш

стійкими щодо пропущених змінних

, похибок вимірювання та наявності ендогенних

змінних серед регресорів.

11.2.2. Модель із фіксованими ефектами

Модель із фіксованими ефектами є моделлю з лінійної регресії, у якій константи

змінюються від одиниці до одиниці спостереження:





  



~...0,

it i it it

iid

x 

Припустимо також, що всі

незалежні від усіх



. Цю модель можна записати в

межах стандартної моделі регресії з використанням фіктивної змінної для кожної

одиниці спостереження і :



  



it j ij it it

ydx  ,

де 1

d  для i

 і 0

d  у решті випадків.

Отже, модель можна оцінити звичайним методом найменших квадратів, однак, у

цьому разі вона міститиме велику кількість невідомих параметрів. Проте можна зробити

простіше: показати, що ті самі оцінки



можна знайти з регресії з використанням даних

у формі відхилень від середніх за одиницями. Спочатку зауважимо, що

  

iii i

y x 

де

(1/ ) ,

itit

yTy

а решта середніх утворюються аналогічно. Далі запишемо



  

it i it i it i

yy xx

МНК-оцінка  , знайдена за цією моделлю з перетвореними даними, називається

оцінкою з фіксованими ефектами. Позначимо її через



. Оцінки

 знаходимо

таким чином:

  

,1,...,

iiiFE

yiNx  .

Оцінки є незміщеними в припущенні, що



M0

it is

x для всіх s і t . Коваріаційна

матриця















  









FE it i it i

β xxxx

де







-оцінка дисперсії збурень











 







it i it FF

x β .

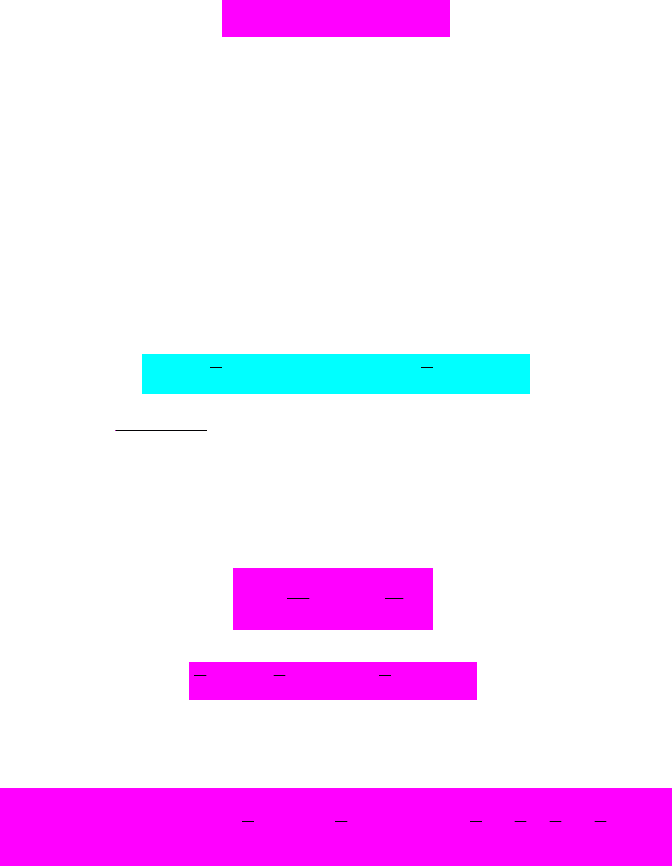
266

При досить необмежених припущеннях одержані оцінки є асимптотично

нормальними. Отже, для перевірки гіпотез можна застосувати стандарті статистики (t-

статистику, статистику Вальда тощо).

11.2.3. Модель з випадковими ефектами

У регресійному аналізі зазвичай припускають, що всі фактори, які діють на залежну

змінну, але які не входять до рівняння явно, можна моделювати за допомогою

збурень. У

нашому випадку це приводить до припущення, що



є випадковими факторами,

незалежними й однаково розділеними стосовно одиниць спостережень. Таким чином,

модель можна записати у вигляді

  

it it i it

y x β







~...0, ; ~...0,

it i

iid iid





,

причому

iit



слід інтерпретувати як похибку, яка складається з двох компонентів:

1). компонента, специфічного для кожної одиниці спостережень, який не змінюється в

часі;

2). залишкового компонента, припускаючи, що він некорельований у часі.

Таким чином, кореляція збурень у часі виникає завдяки ефектам

 , пов'язаним з

одиницями спостережень. Отже, залишилось записати структуру цієї кореляції й

застосувати узагальнений метод найменших квадратів. Найбільш простою процедурою

обчислення є така. Слід знайти оцінки звичайного методу найменших квадратів у моделі

за перетвореними даними:



     

()

it i it i it

uxx

де

1/2

1, 











На практиці



 і



 невідомі, тому їх треба оцінювати.

Оцінку





знаходять із моделі з фіксованими ефектами. Оцінку





можна знайти за

формулою





  



222

ˆˆ

де

e – залишки звичайного методу найменших квадратів у моделі

   ,1,

iiii

yiNx β .

Оцінки, одержані за допомогою описаного варіанту узагальненого методу найменших

квадратів, називаються оцінками з випадковими ефектами; їх позначаємо

β (англ.

random effects estimator). Коваріаційну матрицю знаходимо за формулою

 





 



     





 

11 1

Dˆ .

NT N

RE it i it i i i

ij i

Tβ x xx x xxxx

Ця коваріаційна матриця збігається зі стандартною коваріаційною матрицею, яку

розраховують під час оцінювання моделі за перетвореними даними звичайним методом

найменших квадратів.

11.2.4. Фіксовані ефекти чи випадкові ефекти

Загалом моделі з фіксованими ефектами слід надавати перевагу в тому разі, коли

обрані одиниці спостережень становлять усю або значну частину невеликої популяції

(країни, великої компанії, галузі). У таких випадках наголос часто роблять на

відмінностях між одиницями спостережень. Якщо сукупність одиниць спостережень

утворюють як вибірку з великої популяції, роблячи наголос на граничних ефектах

пояснювальних змінних, то перевагу слід віддати моделі з випадковими ефектами. Однак