Черненко В.Д. Высшая математика в примерах и задачах (том 1)

Подождите немного. Документ загружается.

Гпава 1

1.8. Ранг матрицы

Если в матрице взять какие-либо к строк и столбцов и со-

ставить определитель из элементов, которые окажутся на их пе-

ресечении, то этот определитель называется минором /с-го

порядка данной матрицы.

Из строк и столбцов матрицы можно составить определи-

тели различных порядков, не превышающих наименьшего из

чисел т или п.

Рангом г матрицы называют наибольший из порядков оп-

ределителей этой матрицы, отличных от нуля.

Матрицы, имеющие одинаковый ранг, называются экви-

валентными.Эвив^теятяостъ

матриц обозначается знаком

меж-

ду

ними.

Элементарными преобразованиями называются такие

преобразования, при которых миноры матрицы либо не меняют

своей величины, либо, меняя величину, не обращаются в нуль.

Элементарные преобразования матриц позволяют:

Переставлять местами между собой строки (столбцы).

Прибавлять к какой-либо строке (столбцу) другую стро-

ку (столбец), умноженную на любое число.

Умножать строку (столбец) на число, отличное от нуля.

Вычеркивать строки (столбцы), состоящие

из

одних нулей.

Элементарные преобразования позволяют получить матри-

цу, эквивалентную исходной, для которой легко установить ранг.

Для этого необходимо с помощью элементарных преобразова-

ний привести исходную матрицу к диагональному виду

а„

^12

^22

«13 •

«23 •

«33 •

0 .

•• «1А •

.. а,, .

•• «3* •

•• «** •

•• «.«

•• «2п

•• «з«

тп

где а^=

при i >j; ФФ

при / =/

ОПРЕПЕПИТЕПИ и

МАТРИиЫ.

СИСТЕМЫ

Ранг этой матрицы равен к, так как она имеет отличный от

нуля определитель

А:-го

порядка.

Всякий отличный от нуля минор матрицы, порядок кото-

рого равен рангу матрицы, называется базисным минором этой

матрицы.

Теорема о

базисном

миноре.

Если матрица имеет отличный

от нуля минор порядка

/с,

а все миноры порядка

/с+1,

содержа-

щие данный минор (окаймляющие

миноры),

равны

нулю,

то ранг

матрицы равен к.

Метод окаймляющих миноров. Находим минор второго по-

рядка отличный от нуля, если такой существует, и вычисляем

окаймляющие его миноры третьего порядка, пока

не

найдем сре-

ди них отличного от нуля и т. д.

Если найден отличный от нуля минор порядка к, то вычис-

ляем окаймляющие миноры к+1 порядка. Если все они равны

нулю или таких миноров вообще нет (в случае, когда матрица

содержит к столбцов или к строк), то ранг матрицы равен к,

иначе этот процесс продолжаем.

8.1.

Найти ранг матрицы

Л =

-1

Решение. Поскольку минор второго порядка

УИ.=

2 1|

1 0

= -\ФО,

а оба окаймляющие его миноры третьего порядка равны нулю

2 1 4

1 0 3

5 2 И

= 0,

2 1

1 0

5 2

-1

52 Гпава 1

ТО

ранг матрицы А равен двум, а базисным минором является,

например, Mj.

8.2. Найти ранг матрицы:

а)

-1

-2

-1

8 l^

1 5

-2 3,

б)

^ 3

-1

-3

Решение, а) Переставим первый и второй столбец местами

/"2 2-1 8 О

7 4-2 15

^4 2-1-2 3

2 -1

7 -2

2 4-1

8 О

1 5

-2 Ъ

Чтобы иметь дело с меньшими числами, умножим первый

столбец на ~

(\ 2

2 7

1 4

-1

-2

-1

8 П

1 5

-2 3

Первую строку прибавляем ко второй и третьей, умножая

при этом ее на (-2) и (-1), соответственно

^1 2-1 8 О

0 3 О -15 3

0 2 О -10 2

Умножим вторую строку на—, получим

-1

8 П

-5 1

-10 2

ОПРЕПЕПИТЕПИ и

МАТРИиЫ.

СИСТЕМЫ

8 1

-5 1

О О

Умножим вторую строку на (-2) и прибавим ее к третьей

строке

(\ 2 -1

О 1 О

0 0 0

Вычеркиваем третью строку

^\ 2 -1

О 1 О

Отсюда видно, что ранг матрицы равен г = 2.

б) Поменяем местами первую и вторую строку

( Ъ -\ \ 5Л ( \ 15-1^

-5

-1

5 -1

2 -3

7 9

-1

-1 1

4 2

1 7

-3

Умножим первую строку на 3 и вычтем из второй, затем

прибавим ее к третьей, а к четвертой прибавим первую строку,

умноженную на (-7)

-22

-14

-28

-П

-Л

Умножим вторую строку на

— , а четвертую на -

5 -О

7 -4

-12 -7

Гпава 1

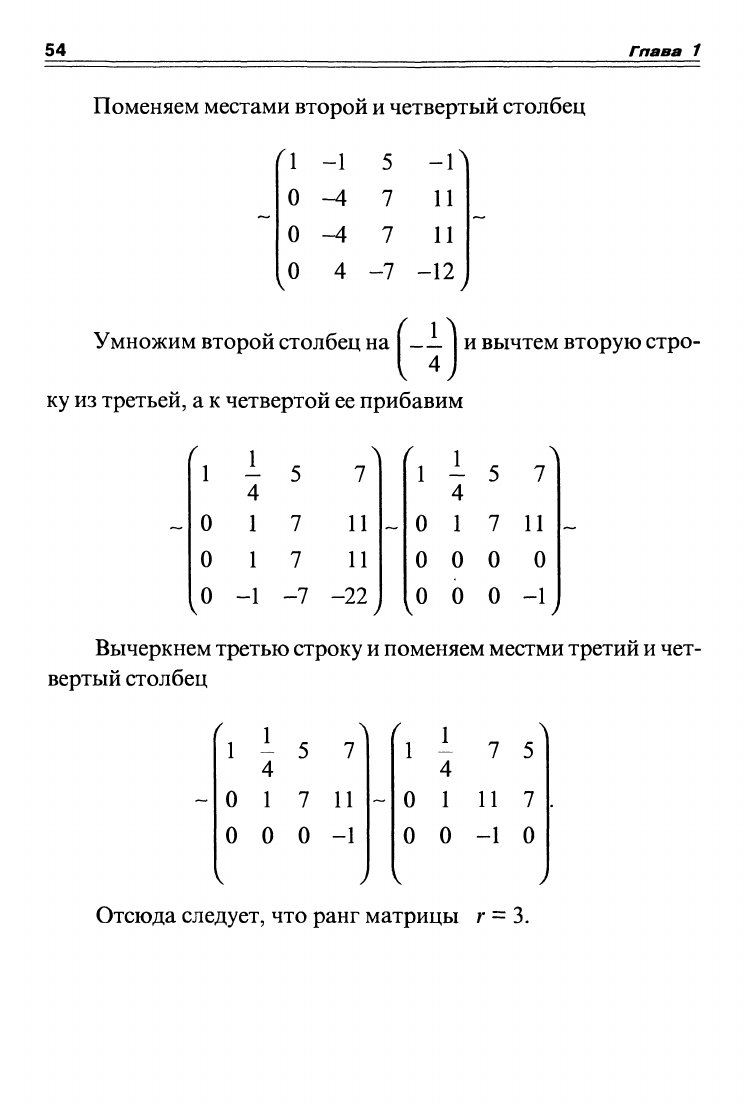
Поменяем местами второй и четвертый столбец

-1

-4

-7

-п

-12

Умножим второй столбец на ( —

и вычтем вторую стро-

ку из третьей, а к четвертой ее прибавим

-1

-7

-22

1 i 5

Вычеркнем третью строку и поменяем местми третий и чет-

вертый столбец

1 7

0 0

-1

1 i 5

0 1 7

0 0 0

-1

)

(

7 5

1 i

О 1 11 7

0 0-10

Отсюда следует, что ранг матрицы г = 3.

ОПРЕПЕПИТЕПИ и

МАТРИиЫ.

СИСТЕМЫ

1.9. Решение системы линейных уравнений.

Теорема Кронекера-Капелли

Рассмотрим систему т линейных уравнений с п неизвест-

ными

Введем в рассмотрение матрицу системы

А =

а,

а^

а,. а,.

а<

*т2

^-In

расширенную матрицу

Б =

а,

•21

'т2

^2пК

тп п

Теорема

Кронекера-Капелли. Для того чтобы система была

совместна, необходимо

достаточно, чтобы ранг матрицы А си-

стемы равнялся рангу расширенной матрицы В, т. е. г {А) = г (В),

Система называется несовместной, если она не имеет ни

одного решения. В зтом случае ранг матрицы А меньше ранга

матрицы В.

Совместная система называется определенной, если она

имеет единственное решение, и неопределенной, если решений

более

одного.

Совместная система будет определенной, если ранг

системы равен числу неизвестных, т.е. г{А)=пи неопределен-

ной, если ранг системы меньше числа неизвестных, т.с.г(А)< п.

Гпава 1

Если все свободные члены равны нулю 6j= Ъ^ ... = Ъ^ О,

то система линейных уравнений называется однородной и все-

гда совместна.

Пусть,

общем

случае,

ранг совместной системы меньше

чис-

ла неизвестных или числа уравнений

< (/iv

m),

причем базисный

минор располагается в

строках и столбцах матрицы ^. Эти г не-

известных

Хр

...

,Xj.

назовем

базисными

неизвестными,

г,

х^^^,...

,х^

назовем

свободными неизвестными

и перенесем их в правую часть

системы уравнений. Решая полученную систему уравнений

(по

фор-

мулам Крамера), определяем базисные неизвестные через свобод-

ные.

Придавая свободным неизвестным произвольные значения,

находим, что решений

этой системы бесконечно много.

Если ранг матрицы А равен рангу матрицы В и г

т, то

выбираем из системы какие-нибудь

уравнений, матрица коэф-

фициентов которых имеет ранг г.

Решение этих г уравнений будет являться решением и ос-

тальных т-г уравнений системы. Если же в этом случае г <п,

то система имеет бесчисленное множество решений.

9.1.

Исследовать систему

.Л/1 I Л"^ """ Л-ч ~~~ tJ f

2л:,

+Х2+ ЗХз

= 4,

2x^

4Хз

=11,

л;,

2^2

Хз

= 4,

2х, +Зх2-7Хз =16.

Решение. Запишем расширенную матрицу системы

^1 1 -1 5^

2 1 3 4

6 = 12 1 -4 11

12 14

2 3-7 16^

ОПРЕПЕПИТЕПИ и

МАТРИиЫ.

СИСТЕМЫ

-4

-3

-4

Прибавим вторую строку

пятой, а третью

четвертой

f\ 1 -\ Ъ\

в~

Разделим четвертую строку на 3, а последнюю строку на 4

f\ \ -\ 5\

2 13 4

Б-Ь 1 -4 И

11-15

Вычтем первую строку из четвертой

последней

^1 1 -1 5^

2 13 4

В~\

11-26

0 0 0 0

Вычеркнем четвертую

пятую строки

(\ 1 -1 5^

B~\l

1 3 4

11-26

Отсюда матрица системы

А~

-2

Гпава 1

1 1

2 1

1 1

-1

-2

1 1

2 1

0 0

-1

Найдем определитель последней матрицы

= 1;^0.

Следовательно, г{А)-Ъ,

Ранг расширенной матрицы также равен г(5)=3, поскольку

только что рассмотренный определитель является минором рас-

ширенной матриы. Следовательно, система совместна.

Для решения системы выберем, например, уравнения

12Xj +

3^3

= 4,

Xj + 2^2 + Хз = 4.

Решая систему по формулам Крамера находим, что

Xj=3,

х^

xf^X. Нетрудно

убедится,

что третье

пятое уравниния при

этих значениях неизвестных тождественно удовлетворяются.

9.2. Исследовать систему

2х, +

2^2

+ 8Хз

- 3^4

9^5

= 2,

2х, +

2^2

4Хз

- ^4 +

3^5

= 2,

Xj + Х2 +

ЗХ3

2X4

ЗХ5

= 1,

Зх, +3X2+5X3-2X4+3X3 =1.

Решение. Найдем ранг матрицы системы и ранг расширен-

ной матрицы

системы.

Для этого запишем расширенную матри-

цу системы

8-392^

2 4-132

113-231

^335-231

В =

ОПРЕПЕПИТЕПИ И MA TPHUbL СИСТЕМЫ

Вычтем из элементов первого столбца элементы второго

столбца

в~

^0 2 8

0 2 4

0 1 3

0 3 5

Матрица А системы будет

А~

(1 8

2 4

1 3

-3

-1

-2

-3

-1

-2

3 2

3 1

3 1>

Разделим все элементы последнего столбца на 3

А~

(1 8

2 4

1 3

V '

Прибавим третий столбец к

А~\

'2 8

2 4

1 3

3 5

-3

-1

-2

четвертому

-3

-1

-2

-1

•

Отнимаем из последней строки третью

А~\

'2 8

2 4

1 3

2 2

-3

-1

-2

-1

•