Черненко В.Д. Высшая математика в примерах и задачах (том 1)
Подождите немного. Документ загружается.

30
Гпава 1
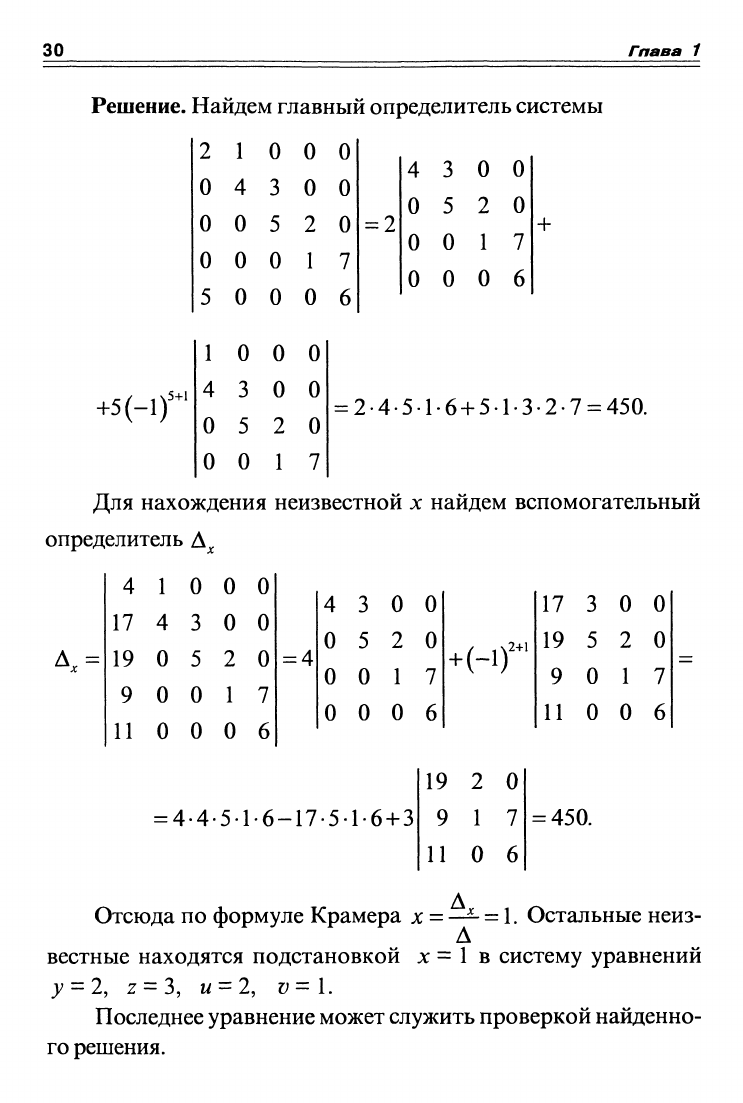
Решение. Найдем главный определитель системы
|2 1 О О 0|
10 4 3 О о|
10 О 5 2 01
10 О О 1 71
5 0 0 0 6
4 3 0 0
0 5 2 0
0 0 17
0 0 0 6
+5(-1Г
2-4-51-6
+ 51-3-2-7 = 450.
10 0 0
|4 3 О О
О 5 2 о|
0 0 17
Для нахождения неизвестной х найдем вспомогательный
определитель Д^
4
1 О О 01
А =
17 4 3 О О
19 О 5 2
01
= 4
9 0 0 17
11 О О О 6
= 4-4-51-6-17-51-6 + 3
4
0
0
0
3
5
0
0
0
2
1
0
0
0
7
6
.(-,Г
3
5
О
О
2
О
17
19
9 0 17
И О О 6
= 450.
19 2 О
9 1 7
11
О 6
Отсюда по формуле Крамера х
=
—^ =
1.
Остальные неиз-
А
вестные находятся подстановкой х =
1
в систему уравнений
y^l,
z = 3, и = 2, v=\.
Последнее уравнение может служить проверкой найденно-
го решения.

ОПРЕПЕПИТЕПИ и
МАТРИиЫ.
СИСТЕМЫ
31
1.3. Основные определения теории матриц.
Сложение и умножение матриц
1°.
Матрицей называют таблицу, состоящую из элементов
а-.,
расположенных в т строках и п столбцах, и обозначают
А =
а,
а
21
1 ^ml
^2
а
а,,
22 *2«
С1
ml
а^
Если т =п,то матрицу называют квадратной; если т-1,
то получим матрицу - строку
если « = 1, то получим матрицу
—
столбец
^21
Если элементы квадратной матрицы удовлетворяют усло-
вию
a-j
=
а.-,
то матрица называется симметрической.
Единичной
матрицей порядка
п
называется квадратная мат-
рица, у которой на главной диагонали стоят единицы, а все ос-
тальные элементы равны нулю
Г1 о ... 0^
О 1 ... О I II если i
=
j;
Е =
О
О
1
а,=^
О если i ^ /.
V
' - J
Нетрудно заметить, что определитель единичной матрицы
любого порядка равен единице det Е^- \.

32
Гпава
1
Две матрицы
AVLB
называются равными, если они имеют
одинаковую размерность и все соответствующие элементы мат-
риц равны между собой, т. е. а.. = 6..
2°.
Суммой двух матриц одинаковой размерности
AVLB
на-
зывается матрица С такой же размерности, получаемая из этих
матриц сложением соответствующих элементов
с..
=
а.г^Ь..
С = А+В.
Например, сумма матриц третьего порядка имеет вид
kl ^2
^13
'
^21 ^22 ^23
[^1 ^2 ^3 ^
+
^Ьи 6,2 ^13 '
^21 ^^22 ''гз
^^31 ^32 ^33 J
=
4l+6ll ^2+^12
«21+^21 ^22+^22
^031+63,
^32+^32
Свойства суммы матриц:
1.
Сочетательный закон
(А+В) + С=А + {B+Q.
2.
Переместительный закон
А+В^
--В+А.
а,з+6,з^
«23+^23
«33+^33 J
3°.
Разность матриц есть действие обратное сложению, т.
е. чтобы найти разность двух матриц одинаковой размерности,
следует произвести вычитание соответствующих элементов
Cy
=
a.j-b,j.
4°.
Умножение матрицы на
число.
Под произведением мат-
рицы А на число к понимается матрица Д получаемая из матри-
цы А умножением всех ее элементов на это число Ь.-= ка--
В
=
кА.
Свойства:
1.
Распределительность относительно суммы чисел
{kj+k^A -kjA +к^,
2.
Распределительность относительно суммы матриц
к(А+В)=кА Л-кВ.

ОПРЕПЕПИТЕПИ и МАТРИиЫ. СИСТЕМЫ
33
5°.
Умножение матрицы на матрицу. Под произведением
матрицы А размерности {тхп) на матрицу В размерности
{nxk) понимается матрица С размерности
(АПХ^),
получаемая
перемножением элементов матрицы А на элементы матрицы В
по правилу
^ч
Х^Л-
т. е. по правилу «строки на столбец».
Таким образом, произведение матриц А
•
В имеет смысл
только тогда, когда число столбцов матрицы А равно числу
строк матрицы В,
В
итоге получается матрица
С,
у
которой чис-
ло строк совпадает
с
числом строк матрицы ^, а число столбцов
с числом столбцов матрицы В :
A-B
= C[^(mxn)(nxk) = (mxk)j.
Например, произведение двух матриц третьего порядка име-
ет вид
Л
«11
«21
«31
«12 «13
«22 «23
«32 «33
6,1 6,2
к, 6„ Ь.
6,3^
22
&,
ь.
32
-'23
^^33
Ъ=М^ Ъ=М2 Ъ=Мз
£=ЛА1 Hi=M2 Х?=Л'Аз
Е-=1«зА I.IM2 Х-=лАз
Свойства:
1.
А{В+С)=АВ+АС;
2.
(В+С)А =ВА-^СА;
3.
(А+В) (C-^D) = AC+AD+BC+BD;
4.
{АВ)С=А{ВСУ
Здесь предполагается, что матрицы
А,
В,
С,
Z>
допускают пе-
ремножение.
6°.
Если размерность матрицы А равна (тхп),то Е^А
=
А
и АЕ^
=
А, т. е. умножение матрицы А на единичную матрицу
есть та же самая матрица А, если порядок единичной матрицы
позволяет перемножение.

34
Гпава
1
3.1.
Найти сумму матриц
Л =
(1 ъЛ
3 5
1 2
^v
)
,
'
Решение.
С=Л+Б=
В
=
(1
4
b
(3 6^
7 3
3
9
3
-2
7
3.2.
Найти разность матриц
А =
2
•2
1
3
4^
7
> \
4
О 1
3
5-2
Решение.
С
=
А-В:
-2
1 3
-5
-2 9
3.3.
Найти произведение матрицы
А =
число
к = 3.
Решение.
3
4 7 1
2
3 5 2
4
1-23
л
на
B
=
kA
=
9
12 21 3\
6
9 15 6
^12
3 -6 9^
3.4.
Доказать равенство
1
-1 2^
4
3 5
= 2
1
-1 2
4
3 5
\
+
3
)
f
1
-1 2'\
3
5
Решение. Выполним указанные действия
J
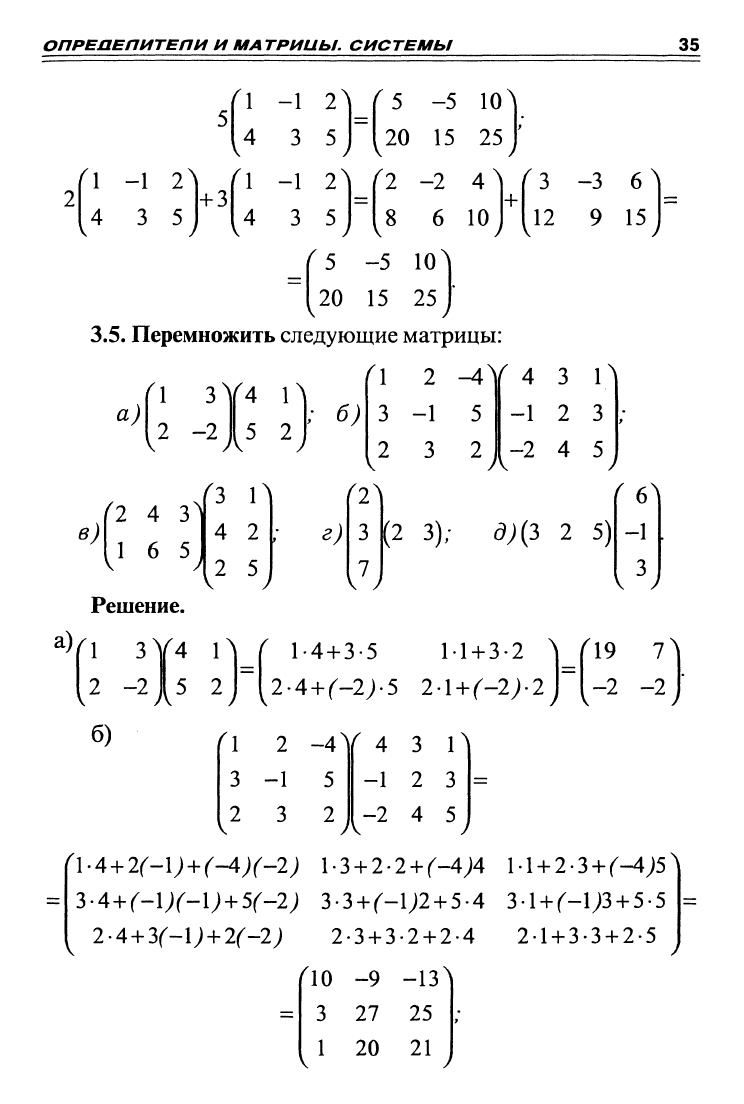
ОПРЕПЕПИТЕПИ И МА ТРИиЫ. СИСТЕМЫ
35
(\
i
14
V
2
{\ -1 2\
+
-
4 3 5
Л
3
4
\ / \
-1 2V
3 5 Г
(5
'2С
/ V
-1 2у
3 5 Г
р
"8
/ V
(Ъ -5
[20 15
-5
10
^
1 15 25
/
-2 4^ Гз •
+1
6 10 12
У
V
10"
«.
3.5.
Перемножить следующие матрицы:
а)
'\ 3
2 -2
Y4
5
\ j\
(Ъ Г
в)
'2 4 3^
16 5 1
V у.
\ 2
> 5
\
Решение.
а)
'\ 3Y4 1
?
-А'> 2
б) .
\ /
/ \
'\
3 •
2
(\
\\
2
; б)
/
\ л
Г
^"^ "
1
/ V
3
2
V
2^
зЬ
7
/
1-4+3-5
2-4+(^-2>5
2 -4 У
-1 5 1
3
2
4
-1
-2
2 ^Y 4 3
-1 5-12
3 2J^-2 4
3);
д){3 2
11 + 3-2 ^
2-l+f-2;-2^
3 Р
2 3
4 !
=
-3 6^
9 15
=
/
1^
3
^
\г
1^6^
5)
-1
3
V у
^19 7^
-2 -2
у
(\-А
+
2(-\)
+
(-А)(-2)
\-Ъ
+ 2-2
+
(-А)А \Л + 2Ъ +
(-А)5\
Ъ-А-\-(-\)(-\)
+
5(-2) 3-3+(^-i;2
+
5-4 3-l
+
f-i;3 + 5-5
2-А
+
Ъ(-\) + 2(-2) 2-3
+
3-2 + 2-4
2-1
+ 3-3 + 2-5
^10 -9 -13^
3 27 25
1 20 21

36
Гпава 1
2 4 3
16 5
г)
Д)
^3 О
4 2
2 5
^2-3+4-4+3-2 2-И-4-2
+
3-5'\
1-3
+
6-4+5-2
1-И-6-2+5-5
(2\
3
(2 3) =
2-2 2-3
3-2 3-3
7-2 7-3
М 6^
6 9
14 21
(1%
ЪЪ\
\Ъ1 38 j
/ лЛ
(3 2 5)
-1
= (3-6 + 2(-1)+5-3) =
31.
, 3 ,
V J
3.6. Даны матрицы
А =
Найти:
а) А (В+С); б) АВ+АС.
Решение, а)
(2 1 3^
5 4 2
V
J
, в
=
( 1 4^
-1 3
5 2
^ )
. с
=
( 2 6^
-1 2
['
')
А(В+С)=
(2 1 3|
5
4 2J
/
1 4
-1 3
5 2
^
/
2 б\
-1 4
5 3
Ч
/J
/"2 1 3
3 10"!
5 4 2
10
2-3 + 1(-2)
+
310 210
+
1-7 + 3-5
5-3 + 4(-2)+210 510 + 4-7 + 2-5
34 42
27 88
б)
АВ^АС=
2 1 Ъ\
5 4 2
1 4
+
2 1
5 4 2
-1 3
5 2
(2Л
+
\(-\)+Ъ-5 2-4 + 1-3+3-3'|
\5Л + А(-\)-^25 5-6+4-3 + 2-2J
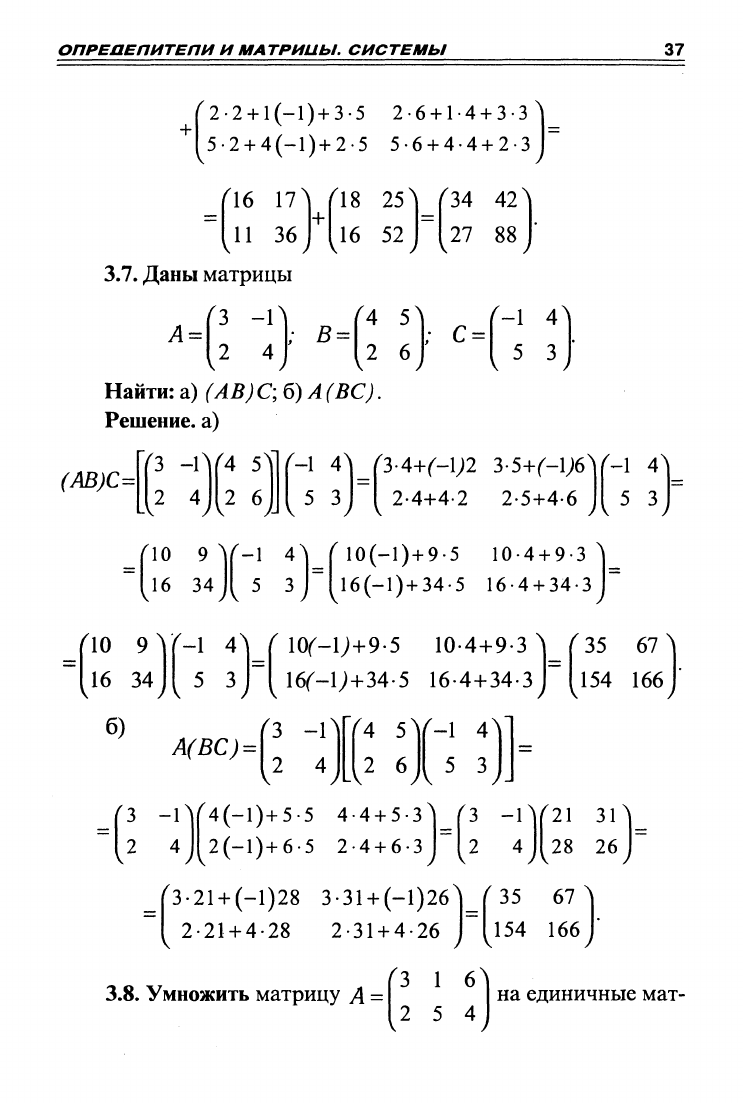
ОПРЕПЕПИТЕПИ и МАТРИиЫ, СИСТЕМЫ
37
11 36
3.7. Даны матрицы
^2-2 + 1(-1) + 3-5 2-6 + 1-4 + 3-3
5-2 + 4(-1)
+
2-5 5-6 + 4-4
+
2-3I
(\в \1\ Г18 25'|_['34 42
"^ 16 52 Г 27 88
А =
3 -1
В
= \
^4 5
2 6
• с=
М 4^
5 3
Найти: а) (АВ)С; б) А (ВС).
Решение, а)
(АВ)С-.
(3 -1
LV
2 4
М 5
1^
6,.
Г-1 4
5 3
(3-4+(-\)2 3-5+r-U6
2-4+4-2 2-5+4-6
-1 4^
5 3
10 9
16 34
(-\ 4
5 3
10(-1)
+
9-5 10-4 + 9-3
16(-1)+34-5 16-4 + 34-3
По 9^
16 34
б)
Г-1 4^
5 3
1"
10('-i;+9-5 10-4+9-3
"1
[l6f-i;+34-5 16-4+34-з]
Г
35 67
"1
154
166
j
А(ВС) =
(3 -О
[2 4
/4 5
LV
2 6
-1 4
5 3
'3 -\Л 4(-1)+5-5 4-4 + 5-3
|2(-1)+6-5 2-4 + 6-3
3 -П
(2\
31
28 26
3-21 + (-1)28 3-31 + (-l)26'|_f 35 67^1
2-21 + 4-28 2-31
+
4-26
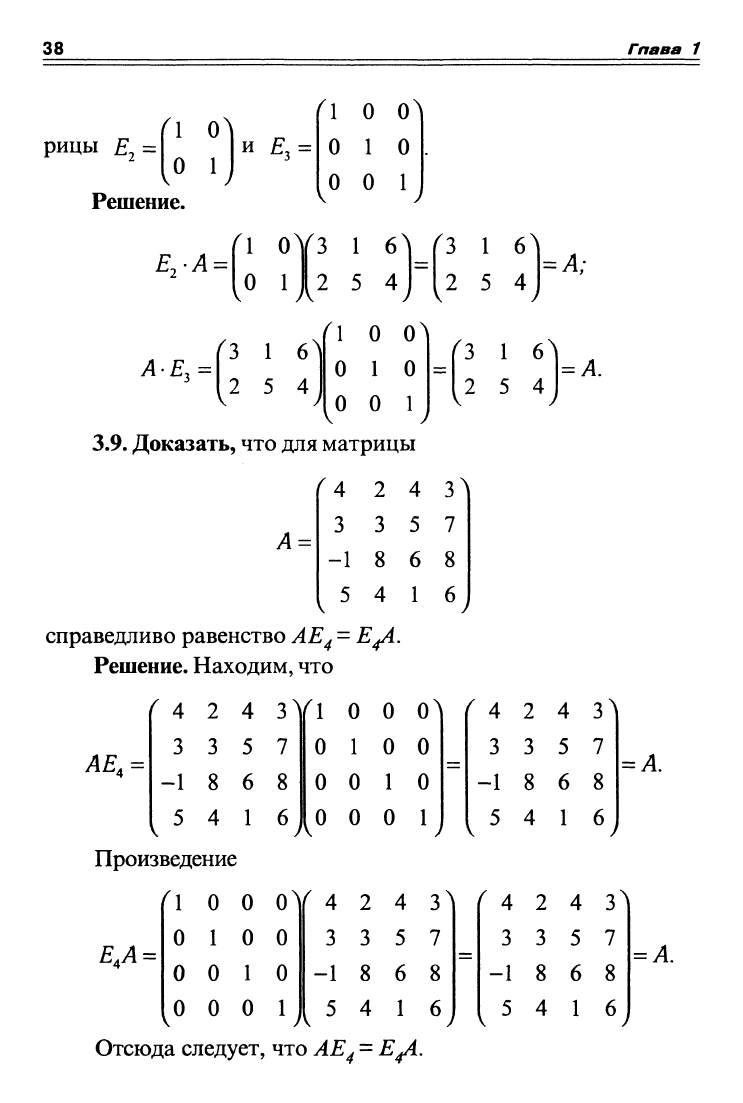
3.8.
Умножить матрицу А =
2 5 4
154 166
на единичные мат-
38
Гпава 1
рицы £• =
(\ О
О
Решение.
и Е,
J
^\ О 0^
О 1 О
О О 1
Е^-А
=
(\
1^
;i
V
3 1
2 5
J
4
^3
2
V
\=А;
АЕ,=
(Ъ 6Л
4
I
О
0 0\
1 о
о о 1
3.9.
Доказать, что для матрицы
^4 2 4
12
4
= А.
А =
3
-1
5
3
8
4
5
6
1
3^
7
8
6
справедливо равенство АЕ^
=
Е^.
Решение. Находим, что
АЕ,=
^ 4
3
-1
5
А
\
л
2 4
3 5
8 6
4 1
Произведение
''I О О OY 4
0 10 0
0 0 10
0 0 0 1,^
1
0
0
0
0
1
0
0
0
0
1
0
0^
0
0
1
J
(
V
Е,А
=
3
-1
5
2
3
8
4
4
5
6
1
3
-1
5
^ 4
3
-1
5
2
3
8
4
4
5
6
1
з^
7
8
6
= А
2
3
8
4
4
5
6
1
3^
7
8
6/
= А
Отсюда следует, что АЕ^ = £^^.

ОПРЕПЕПИТЕПИ и
МАТРИЦЫ.
СИСТЕМЫ
39
3.10. Найти А\ А =
Решение. Находим
1 4Yl 4'\
(\ 4^
3 2
А'=\
3 2
А'
=
(и 12¥l 4^
9 16
3 2
Г1
+
12
4+8'\
3
+ 6
12
+ 4
ЛЗ + 36
52
+ 24^
9 + 48 36+32
(\Ъ \1\
9 16
57 68
3.11.
Найти значение матричного многочлена 2А^+4А+ЗЕ,
^1 -1 1^
если А =
единичная матрица.
Г О -10 4^
• 2А'
4А:
4^4^
8 12 4
4-4 8
)
;ЪЕ
=
(ъ 0 0"!
0 3 0
0 0 3
V J
12ЛЧ4Л +
3£:
18
^7
24
12 14
-12 8
-14 8"!
27 18
-16 19
1
*4*
Транспонирование матрицы
Транспонировать матрицу А — значит все ее строки / сде-
лать столбцамиу с теми же порядковыми номерами
д..
=
а.^'".
Свойства:
1.
Если матрица А имеет размерность (т х п
),
то
матрица
А"*,
будет иметь размерность (/г х m
);
2.{А"Т
=
А;
