Черненко В.Д. Высшая математика в примерах и задачах (том 1)
Подождите немного. Документ загружается.


570
Гпава 10
H-4r'-2k'
(Г+1
откуда
1
+ 4/^-21
+D)-^{Et +
F){t^
+
At^
+
Bt^
+ Ct + D
Et + F
t' =
{3At^
+ IBt +
C)(?'
+1) -
AtiAt"
+
Bt^
+
C/
+
0 = E,
-2l = 3A-4A + F,
0^2B-4B
+ 2E,
4 =
3A
+ C-4C + 2F,
0 = 2B-4D + E,
\ =
C
+ F.
Отсюда:
A
=
14,
B =
0,
C =
S,
D =
0,
E =
0,
F = -1. Таким
образом.
1 = 4
\4t'+St
dt
+
'6t
r dt
r+1)
2t{7t^+4)
-7arctg/
к
С
2 1"^
Учитывая, что t = , и переходя к переменной х, окон-
3 +
JC
чательно получим
I = -{\9-Зx)^Jз-2x-x^ -28arctg J^-^ +
C.
. rx^+l dx
интегралы: a) . ;
Ч-&
7.4. Найти
(jc'-l)^
WXV3JC^+1
1
Решение, a) Воспользуемся подстановкой
x-\-
— =
t,
—T—dx
= dt.

НЕОПРЕПЕПЕННЫИ ИНТЕГРАП
571
д:'+1
Выведем некоторые нужные соотношения
„2
. X
•t.
x'+\
=
{t^-l)x\
1
х^
+
1
dx
rx+i
ах _r tat
, тогда интеграл примет
вид
tdt
Сделаем
еще
одну замену
t^ -2
=
z^, tdt
=
zdz и
предста-
вим интеграл
в
виде
U-V2I
z'-2
2л^
In
z
+
4i
+c.
Переходя
к
переменной
t, а
затем
к х,
будем иметь
1 (V?^-V^)
1
I=-^\xi^
г^ г-^+С =
—Win
2ч/2
Г-4
2л/2
У1Х'+\-ХУ/2
х'-\
+
С.
1
x' + l
б) Воспользуемся подстановкой
х—
=
t,
—г—
dx
=
dt
Введем некоторые дополнительные соотношения
хЧ1
х'-\
=t.
л/л:'*
+
Ъх^
+1
=
xvr^ +
5,
=
л/г^
+
2
.
Интеграл
в
этом
слу-
X
чае примет вид
{х^-\)dx
г ^й?/
WJCVSJC'
+ I •'
л/?+2у[?~+5'
Сделаем еще одну замену
t +2
=
z , tdt
=
zdz,
тогда интег-
рал преобразуется
к
виду
dz
'=i
yfT^
=
ln
z +
Vz^+S
+c.

572 Гпава 10
Переходя к переменной
Г,
а затем к
jc,
получим
/=:1П
+ С =
1п
х'+1 + л/хЧЗх'+1
+
С.
10.8.
Интегрирование тригонометрических
функций
1°.
Интеграл от четной степени sinx, cosx можно найти
путем понижения степени вдвое по формулам
2 1 1 \
sin х = —(l~cos2x), cos х =
—(l
+
cos2x).
(1)
2°.
Интеграл от нечетной степени sin
х, cos х
можно найти
путем отделения от нее одного множителя и замены его произве-
дения на дифференциал новой переменной.
3*^.
Интегралы вида J sin'"
х
cos"
xdx можно найти по прави-
лу (1°), если тип оба четные неотрицательные числа, или по
правилу
(2°),
если
т или
п
(или и тип)
нечетно.
Если
т-\'П
=
-Ik,
т. е. четное отрицательное
число,
то целесообразно использовать
dt
подстановку tgx
=
t или ctgx = r, откуда dx
=
^ ^-^^
^ - ~. 2
•
В общем случае интегралы данного вида, где тип
целые числа, находятся
с
помощью рекурентных формул, кото-
рые выводятся интегрированием по частям.
4°.
Если подынтегральная функция зависит только от tgx
или
ctg
X,
то применяют замену tg
х
= / или ctg х = /.
5°.
Если интеграл имеет вид fi?(sinx,cosx)c?x, где sinx,
cosx входят только в четных степенях, то применяется подста-

НЕОПРЕПЕПЕННЫЙ ИНТЕГРАЛ 573
новка tgx = /, ax
=
г-, поскольку sm x и cos x выражают-
1
+ r
. 2 ^' 2 1
СЯ
через tgjc рационально sin x
=
j и cos x
=
j,
6°.
Если интегралы имеют вид: {sin ах cosbxdx;
J sin ax sin
bxdx;
J
cos
ax cos bxdx, то их можно найти путем раз-
ложения на слагаемые по формулам:
sin ах
cos
bx
= — (sin{a
- b)x
+
sin(a
+
b)x),
sin ax sin bx
=
— (cos(a - b)x - cos(a + b)x),
cos ax cos bx
=
— (cos(a - b)x
+ cos((2 +
6)x).
(2)
7^. Интегралы от рациональной функции вида
R{sinx,cosx)dx с помощью подстановки tg~-/ всегда сво-
дятся к интегралам от рациональной функции, т. к. sin
х, cos
х и
dx выражаются через t рационально
2t 1-/
2
sinx = -, cosx =
2
l+r 1+^
2dt
dx
=
—^, (3)
l
+
r
Рассмотренная подстановка позволяет проинтегрировать
любую функцию вида /?(sinx,cosjc), поэтому ее иногда назы-
вают «универсальной тригонометрической подстановкой».
8°.
Интегралы от произведения трех тригонометрических
функций могут быть найдены по формулам

574 Гпава
10
J
COS ax cos bx cos cxdx
=
1
sm(a+fe+c)x sin(6+c-a)jc sin(«+c-Z?)x sm(a+fe-c)x
V
Vc,
a+Z7+c
b+c-a a+c-b a+b-c
J
cos
ax sin
bx sin
cx(ix =
_ irsin(a+Z7-c)jc sin(a+c-6)x sin(a+6+c)x sin(6+c-a)x
4(^
аЛ-Ь-с
a-\-c-b
a+b+c b+c-a
I
sin
ax
cos
Z)x cos cxdx
=
_
1
[^cos(a+Z?H-c)x cos(Z7+c-(2)x cos(a-\-b-c)x cos(a+c-Z?)x
4(^
а+бч-с 6+c-a аЛ-Ь—с a+c-b
J sin ax sin
bx sin cx^ix
=
_ l(^cos(a+6+c)x cos(a-Z)+c)x cos(Z?+c-a)x cosi
Vc,
ia+b-c)x\^
a+b-c )
41 a+6+c a-b+c b+c—a
8.1.
Найти интегралы:
a)
jsin'^xJx;
6)
Jcos^xJx;
в)
I
cos^xsin'^xJx;
r)
[ sinxcos^xJx;
д) |
T—dx\
e)
|tg^5x(ix.
J
J J cos X ^
Решение, a) Пользуемся формулами тригонометрии для по-
ловинного угла
J sin^
X(ix
= j(sin^
х)^бйс
= — J (l-cos2x)^<ix =
=
—
(l-2cos2x + cos 2x)^ = —(x-sin2x)4-—
cos
2xdx =
4J
4 4J
=—(x-sin2x)+-J(l + cos4x)fitc
=
—(x-sin2x)+-(x+—sin
4x)
+
C.
6) Отделяем от нечетной степени один множитель первой
степени и вносим его под знак дифференциала
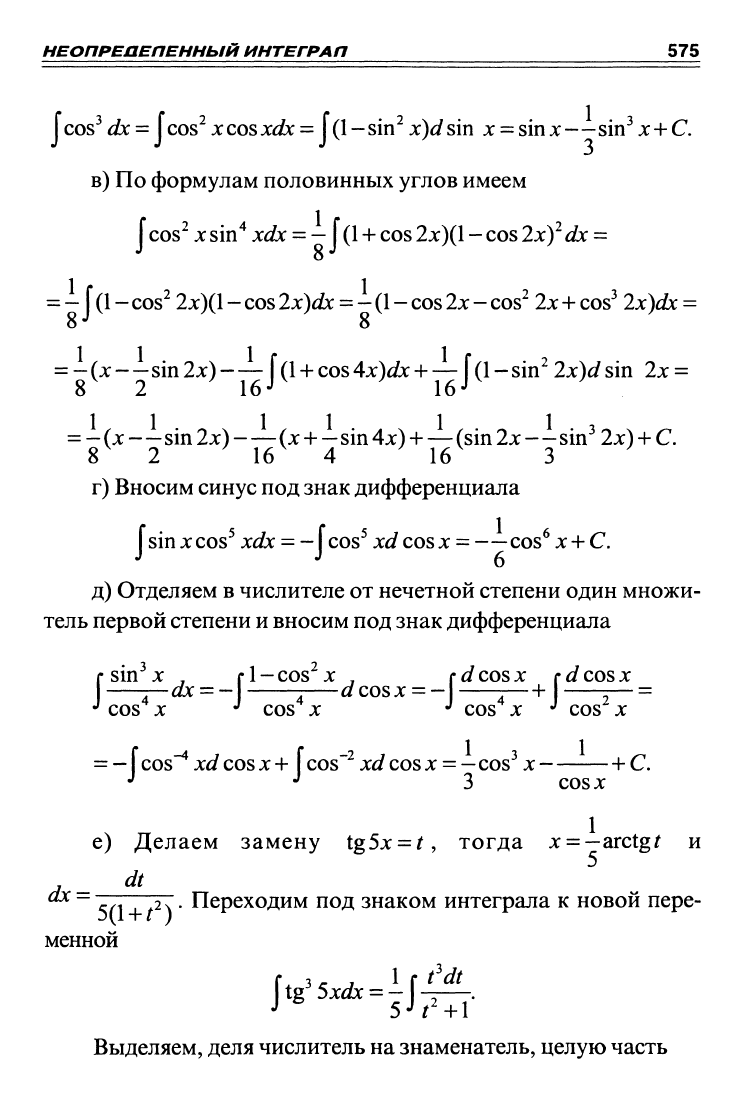
НЕОПРЕПЕПЕННЫЙ ИНТЕГРАП 575
jcos^
dx
= J
cos^ xcosxdx =
J (1
-sin^ x)dsm x
=
sin x—sin^
jc +
C.
в) По формулам половинных углов имеем
J cos^
X
sin"*
xdx = — J
(1
+ cos
2JC)(1
- cos
Ix)^
dx =
1
с J 1 2 1
= -J(l-cos 2x)(l"-cos2x)d!x: = --(l-cos2jc-cos
2jc +
cos 2x)dx =
= -(x—sin2x) \(l
+
cos4x)dx
+
— | (1-sin^ 2jc)^fsin 2x =
8 2 16J \6^
= —(x—sin2x)
(л:
+—sin4x)4- — (sin2x—sin^ 2x)
+
C.
8 2 ' 16 4 16 3
r) Вносим синус под знак дифференциала
Г sin
X
cos^
xdx = -J cos^ xd
cos
x = —
cos^
x + С
д) Отделяем в числителе от нечетной степени один множи-
тель первой степени и вносим под знак дифференциала
fsin^x , fl-cos^x , fJcosx fJcosx
J 5-^ = -J 4 ^cosx = -J ^ +
J
—
=
•' cos X •' COS X •' cos X •' COS X
= -1
cos"^
xd
COS X
+
I
cos"^ xd cosx = ~cos^ x + С
•' •' 3 cosx
е) Делаем замену tg5x
=
t, тогда x = —arctgr и
~ sn-i-/^^
•
Переходим под знаком интеграла к новой пере-
менной
\tg^ 5xdx-- \— .
Выделяем, деля числитель на знаменатель, целую часть
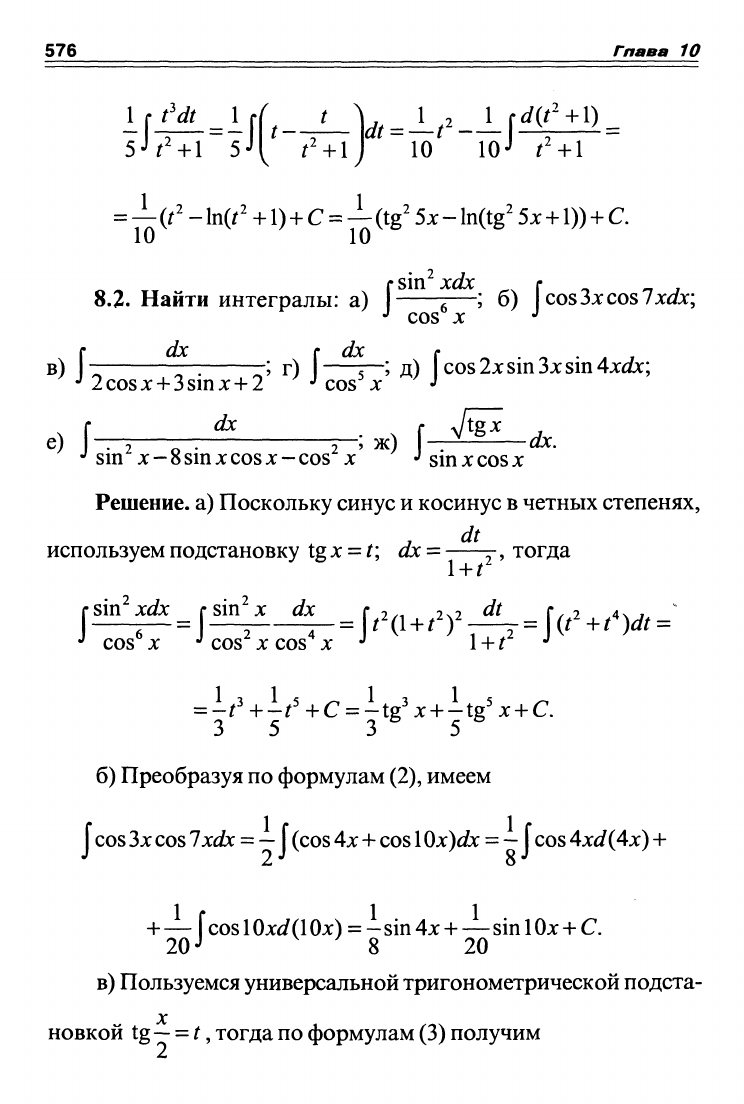
576
Гпава
10
л
к
''+1у
10
loJ гЧ1
\_
10
=—(г'
-
1п(г'
+1) + С =—(tg' 5
JC
~ ln(tg' 5х
+1))
+ С.
10
•
sin^ xt/x
f sin ЛОЛ
f
8.2. Найти интегралы: а) 1—;
б)
cos3xcos7xJx;
^ cos
X •'
f
с/х с dx с
в)
к; ^ ;
г)
с—;
д) cos2xsin3jcsin4xfii!x:;
•^
2cosx4"3smji(:
+ 2 -^
cos
х J
J
CI
dx
sin^
X
-
8 sin X cos
x
-
cos^
-; ж)
— dx.
X J sir
sin
X cos X
Решение, a) Поскольку синус и косинус в четных степенях,
dt
юльзуем подстановку
tg х
=
^;
dx
=
^, тогда
fSin^xJx fsin^x
dx
с j.^
i^i dt
с, 2 4ч т
J ^—= J—-2
—=\t\^^ty—^=\{t'+t')dt
=
•^ cos X •'cos xcos X
-^
1
+ /
•'
= -^4~^4C = -tg'x + -tg'x
+
C.
3
5 3^5^
б) Преобразуя no формулам
(2),
имеем
J
cos
3x
cos
Ixdx =—J
(cos
4x
+ cos
1 Ox)d!x = - J
cos
4xJ(4x)
H-
+— |cosl0xt/(10x) = -sin4x
+—sinlOx
+ C.
20J
8 20
в) Пользуемся универсальной тригонометрической подста-
новкой
tg—
= ^, тогда по формулам (3) получим

НЕОПРЕПЕПЕННЫИ ИНТЕГРАП
577
1
dx
2cosx4-3sin
=
2f :
;inx+2
^ A-t
dt
•=i\—
dt
ILJL
2^L 2 "•'2-2/46^+2+2?'
1+/'
l+t^
dt 1
:f-^ = -ln|3? + 2|+C = -In
J
3^
+ 2 3 ' ' 3
|3<gf^2
+c.
r) Воспользуемся обобщенной формулой интегрирова
ния (13)
с dx sinx 3 с dx sinx 3^
—г-= т-+-\
COS
i X 4cos X 4''COS X 4cos x 4\^2cos x 2*'cosx
sinx 1 f ^ ^
+7J
sin
X
3f sin
X
-+-
1
+—ln|tgx + secx| +C^
— T 1 1
4cos X 4\^2cos X 2
д) Пользуясь формулами пункта
(8"^),
имеем
I
cos 2х sin
Зх
sin 4xdx = — (sin(2 +
3
- 4)x
-h—sin(2
+ 4 -
3)x
-
J 4 3
—sin(2 +
3
+ 4)x—sin(3 + 4-2)x) + C = -(sinx + -sin3x-
9 5 4 3
—sin 9x—sin 5x)
+
С
9 5
e)
Разделим числитель
и
знаменатель на cos~ х, будем иметь
f ^tgx f J(tgx-4) ^ 1 ^
J tg^ x-8tgx~l J (tgx-4)^ -17 2л/17
tgx-4-^/Г7
tgx-4
+
Vl7
:)
Умножим числитель и знаменатель на
cos х,
получим
r''^dx= \^digx= \tgKdtgx
=
24^
+
C.
^ sinxcos X ^ tgx -^

578 Гпава 10
10.9.
Интегрирование гиперболических
функций
р.
Интегрирование гиперболических функций производит-
ся аналогично интегрированию тригонометрических функций.
Интегралы от квадратов
и
других четных степеней sh
х,
ch х на-
ходятся применением формул:
ch^x-sh^x = l; sh2x = 2shjcchx; ch^jc = —(ch2x
+
l);
sh^x = —(ch2x-l); sch^x =
l--th^x;
csch^x =
l-cth^x.
Интегралы от нечетных степеней sh х, ch х находятся так
же,
что и интегралы от нечетных степеней sin х,
cos
х.
2°.
Гиперболические подстановки могут пременяться при
нахождении интегралов вида
^R\x,yjx^ -a^^dx —подстановкой x = achr;
J
/г
[X,
yjx^
-^a^\dx — подстановкой x =
дг
sh x;
J 7?(x,л/л -X \dx—подстановкой x = athx-
^ , 1 х
+
л/х^+а^
При этом: если x
=
asht,
то
^
= In ,
а
. х + Ьл/х^-л^
если x = achx, то t
=
m .
а
9.1.
Найти интегралы: a)jsh^2xt/x; б) jsh^'ch^x^x;
в) Ith'^xdx; г) [-; -; д) [-;—; е) {x^shxdx;
J ^ chx-fl
-^
shx •'
ж)
I
л/chx-ltic; з) | ; и) f sinxshxJx.
•' •'chx
+
shx ^

НЕОПРЕПЕПЕННЫЙ ИНТЕГРАП
579
Решение,
а)
Пользуясь формулами понижения степени, имеем
Jsh^2xtic = -|(ch4jc-l)d[x:=- --|ch4jc<i4jc~x =- -sh4x~x +C
б) Внесем ch x под знак дифференциала, тогда будем иметь
J sh^
X
ch^
xdx = J sh^
X
ch^
jc<i
sh x =
J
sh^ x(l +
sh^
x^d sh x =
=
I
sh^ XJ sh
X
+
sh"^
xt/ sh
X
= — sh^
X
+ - sh^
X
+ C.
J 3 5
Ч
>-.
t dx . dt
в) Сделаем замену th x =
^;
—^— = dt\ dx = -—-, тогда полу-
чим
|шЧ*=0=-|;
t+\ +
it =
-
\-t'
'e 1,
v3 2
/-1
/+1
l+C
=
-th^x+thx+—In
3 2
thx-1
thx +
1
+ C.
r) Преобразуем подынтегральную функцию по формулам поло-
винных углов
dx
Jchx+l •'
X 2
2ch^-
2
Д)
f—=
J
fi?X
2 sh
—
ch
—
2 2
ch —Jx
=J—-—=1
2 2
Jth-
•2-
= In
th
th-
+ C.
e) Воспользуемся дважды формулой интегрирования по частям,
принимая х^ = и, sh xdx
=
dv, Ixdx
=
du, v
=
ch
x.
Будем иметь
Г
jc^
sh xdx =
д:^
ch
jc —
2j X ch xdx.
