Черненко В.Д. Высшая математика в примерах и задачах (том 1)

Подождите немного. Документ загружается.

600 г пава 11

Несобственный интеграл существует или сходится, если

существует конечный

предел.

Если несобственный интеграл ко-

нечного предела не имеет, то интеграл расходится.

Для других бесконечных интервалов несобственные интег-

ралы выражаются аналогичным образом

b b

\ f{x)dx= lim \f{x)dx\ (2)

—oo a

j f{x)dx

J f(x)dx + J f(x)dx, ^2)

С геометрической точки зрения определенный интеграл

f(x)dx выражает площадь области, ограниченной кривой

f(x)

О,

прямыми х

а, х

= Ь

и осью абсцисс. Несобственный

интеграл в этом смысле выражет площадь неограниченной об-

ласти, ограниченной кривой у

f(x), осью абсцисс и прямой

а.

2°.

Если функция f(x) имеет бесконечный разрыв в точке

с, принадлежащей отрезку

[а,Ь]

и непрерывна во всех дру-

гих точках этого отрезка, то интеграл от функции f(x) называ-

ется несобственным интегралом второго рода и вычисляется

по формуле

b с-е b

\ f(x)dx

lim f f(x)dx

lim f f(x)dx, (4)

где £ —произвольная бесконечно малая величина.

Геометрически несобственный интеграл (4) есть сумма пло-

щадей двух фигур, ограниченных графиком функции у

f(x),

прямыми х

а,

= 6, вертикальной асимптотой х

с и осью

абсцисс.

При с

а или с

b несобственные интегралы равны

ОПРЕПЕПЕННЫЙ ИНТЕГРАП 601

Ь Ъ b Ъ-е

I/(x)d!x = lim \ f{x)dx\ \f{x)dx^\\xs\ \ f{x)dx\

a a+e a a

3°.

Признаки сходимости и расходимости несобственных

интегралов.

Пусть при а<х<

+00

имеет место равенство f(x)

<р(х),

тогда из сходимости интеграла | (p(x)dx следует сходимость

интеграла | f(x)dx, а из расходимости [ f(x)dx, следует рас-

ХОДИМОСТЬ I (p(x)dx

Если при а<х<-{-оо существует конечный предел

lim =к (О<

А:

<+оо), то интегралы | f(x)dx и \ (p{x)dx

(р(х) •'^ •'^

сходятся или расходятся одновременно.

Если при X—>оо функция /(х)>0 имеет вид

f(x)

-^— (а >0), то при а >

и (р(х) <с<

+оо

интеграл

I f{x)dx сходится, а при а <

и <p(jc) > о

расходится.

Если сходится интеграл J

|/(х)|

dx, то тем более и сходит-

ся и интеграл [ f(x)dx. Последний интеграл называется абсо-

лютно сходящимся, а функция f(x) — абсолютно

интегрируемой в промежутке [д,+

оо[.

Признак Абеля. Если функции f{x) и ф(х) определены

на отрезке

[а,

оо),

причем функция /(х) интегрируема на этом

отрезке, т. е. интеграл | f{x)dx сходится, а функция <р(х) —

602 Г пава 11

монотонна

ограничена |(р(х)|< L {L - const, хе[а,<^)), то

интеграл | f{x)(p{x)dx сходится.

6. Признак Дирихле. Если функция f(x) интегрируема на

любом конечном отрезке [а,Ь] ф>а), причем интеграл

г^

f{x)dx\<L (L — const, a<b<^) оказывается ограничен-

ным, а функция (р{х) монотонно стремится к нулю при х ->

оо ^

то интеграл f f{x)(p{x)dx сходится.

Признаки сходимости и расходимости несобственных

интегралов от неограниченных функций аналогичны.

Если для достаточно близких к с значений х функция /(х)

имеет вид f{x)

-—^—^ (а > 0), то при а<1 и

(р(х)

<L<

н-оо

(c-xf

{L —

const)

интеграл f(x)dx сходится {a<c<b), при a >

(p(x)

>L>0 интеграл расходится.

6.1.

Вычислить несобственный интеграл или установить его

. г~ x^dx ^ч 7 dx л f^ "^ ,

расходимость: а) -; б) Г • в) хе ^dx;

+ х' £х'+2х +

J-

dx ^ roo dx

Г__ах__

rdx

Решение, a) Преобразуем подынтегральное выражение и

воспользуемся формулой (1)

г- x^dx 1 ,. р^ dx^ 1 ,. ^ з1^

= - lim г-т = - lini arctg

+ х'

S^-^-Ji

(-^

) 3^^- 1^

7Г

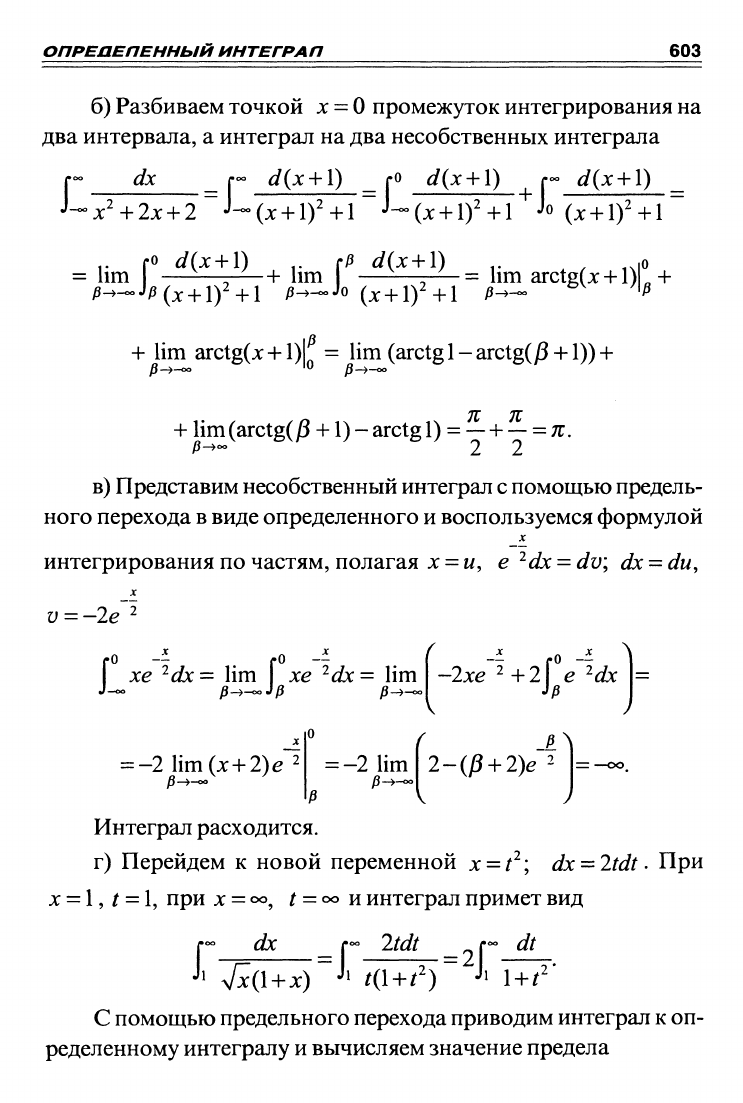
ОПРЕПЕПЕННЫИ ИНТЕГРАП

603

б) Разбиваем точкой х =

промежуток интегрирования на

два интервала, а интеграл на два несобственных интеграла

р dx _р ^(jc + l) _ fo J(x +

р d{x-\-\)

J-x'+2x

2~J-(x

+ l)'+l"J-(x + l)'+l^-'o (x + l)4l~

= lim —^^—r-^^+ lim

—^—T-^—^

lim arctgfx

+1)1

^-.-co J^ (^ + 1)2+1 /^-^- Jo (;c + 1)2+1 /^^- '^

+ lim arctg(x + l)|f = lim (arctgl~arctg(/3^-l)) +

+ lim (arctg(

+1) - arctg

—

л:.

в) Представим несобственный интеграл

помощью предель-

ного перехода в виде определенного и воспользуемся формулой

интегрирования по частям, полагая х

и, е ^dx

dv; dx = du,

xe ^dx = lim xe ^dx = lim

—Ixe 2+2 e ^dx

2 (

0 --

= -2 lim(x

2)e 2 = -2 lim

2-(j8 + 2)e 2

Интеграл расходится.

г) Перейдем к новой переменной х = /^; dx

2tdt.

При

= 1, / =

при

оо^

/ =

оо

и интеграл примет вид

р йЬс _ р 2/(i/

Г *" ^^

С помощью предельного перехода приводим интеграл к оп-

ределенному интегралу и вычисляем значение предела

604

Гпава

гР dt

(ж n

д) Сделаем следующие преобразования

2 lim(arctg

- arctg

= 2

I г—=lim| ln^jct/lnx = — lim—-

•^9 xln'jC ^-^-•'9

= — lim

2^->'

^-^~

In" jc

1 1

l^ln'jS

In'9 J 21n'9

81n'3'

6.2. Вычислить интегралы:

Решение, a) Поскольку в точке x = 1, принадлжащей про-

межтку интегрирования, функция терпит разрыв, то интеграл

относится к несобственным интегралам второго рода и вычис-

ляется по формуле (4)

Г-7=£=

= итГ"(х-1)"^^гг + итГ (;с-1)'^^ =

= lim3V^r+lim3V^f =31im(^l-e-l~V^)+

e^O 1-1 e->0 ll+e £->0

lim(Vl -

+ e-l) = 3(^2 +1).

6) Подынтегральная функция терпит разрыв в точке х = 1,

т. е. на конце промежутка

[1,2].

Следовательно, интеграл отно-

сится к несобственным интегралам второго рода и вычисляется

f2 dx ,. f2 Jinx

=limlnlnjcl, =lnln2~

f =limf =limlnlnjd^ =lnln2-limlnln(l+e)=lnln2+oo=c

Jl vln V

£^OJl+£

In V £-Ю '^+^ £-Ю

xlnx ^^•'1+e Inx ^-^

ОПРЕПЕПЕННЫЙ ИНТЕГРАП

605

в) При

л:

= о подынтегральная функция обращается в бес-

конечность, во всех остальных точках промежутка [0,1] она не-

прерывна. Следовательно, имеем

1 dx

fJ dx .. fi dx ,.

—. 7 = lim — = lim

•'o x^ - 3x^

^-^0

(x - 3) ^^0

1 1

- + -

[ 9x 3x' 9(jc-3)

\dx

1 Г li 11 111 v"^

= lim —mxH

—lnuc-3

^->n 9 3x 9 '

1 li .

= - + -ln2-

3 9

-lim

111,

111 .Л 1^

lne+-lne-3 =-

3e 9 9 ' 'J 3^

1+-1п2+-ит(1пв+1)"-1пз1=-

3 3^^ 3

т. е. интеграл расходится.

г) Подынтегральная функция непрерывна

промежутке [0,2]

за исключением точки

д:

= 1, в которой она терпит разрыв. Сле-

довательно,

f2 dx ,. fi-e dx ,. г2

--Z = lim + lim -

x-3f-4

Первый интеграл равен

= —limln

jc-5

x-1

\\-£

+ 4

= —lim In

£-^0

-ln5

rl-e

lim ,

s-^oJo

(^х-Зу-Л

4^-^o

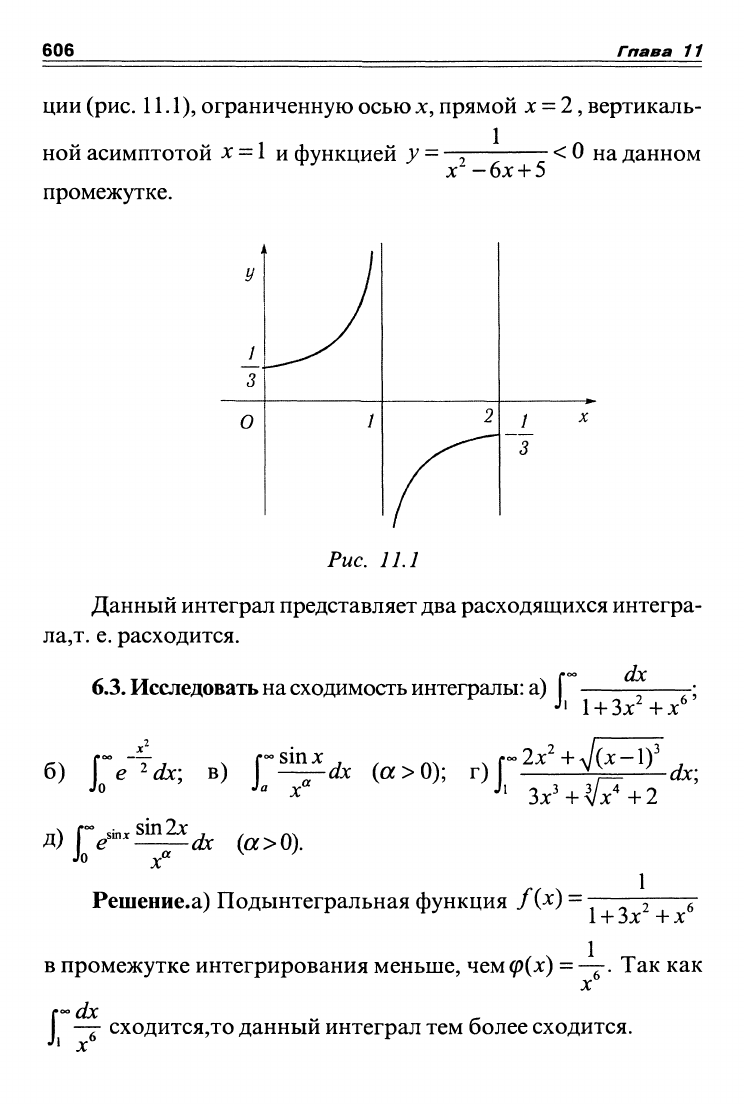
представляет неограниченную площадь криволинейной трапеции

(рис.

11.1),

ограниченную

осью>^,

кривой у = — >

на дан-

X -бх

+ З

ном промежутке, осью абсцисс

вертикальной асимптотой

д:

= 1,

Второй интеграл равен

= —limln

jc-5

x-1

= —lim

4 e-^O

ln3-ln

£-4

lim I - - ..XX.

£->0 Jl+e (х

—

ЗУ—4 4 ^-^0

и представляет неограниченную площадь криволинейной трапе-

606

гпава 11

ЦИИ

(рис. 11.1), ограниченную осью х, прямой х = 2, вертикаль-

ной асимптотой

и функцией у = —^—;—— <

на данном

промежутке.

X -6х

+ 5

Рис. 11.1

Данный интеграл представляет два расходящихся интегра-

ла,т. е. расходится.

6.3.

Исследовать на сходимость

интегралы:

а) -;

J»

+ Зх'+х'

б)

l^'^'dx;

в) [^dx (а>0); г)|^

>2хЧл/(х-1)^

3x4^^

dx;

sin2x

^)p..smzx^ («>0).

Решение.а) Подынтегральная функция f(x) -

+ Зх'+х'

в промежутке интегрирования меньше, чемф(х) =

—т-.

Так как

—7-

сходится,то данный интеграл тем более сходится.

ОПРЕПЕПЕННЫИ ИНТЕГРАП

607

б) Разобьем промежуток интегрирования

оо -fl 1 -:^ со -^

I е ^dx= \ е ^dx+ \ е ^dx.

Jo Jo Ji

Первый интеграл в правой части не является несобствен-

ным, а второй сходится, так как е ^ <е '^ при

л:

I е ^dx = -2 lim е

й->оо

-2 lim

е ^ -е '

= 2е\

Следовательно, данный интеграл сходится.

в) Пользуясь признаком Дирихле, полагаем /(х) = sin х,

^\^) = —^. Поскольку

функция —^, монотонно убывая, стремится к нулю при х -^

©о ^

>sinx

г6 I , ,

sinxJx = cosa-cosZ? <2 (a<b<oo)\i

Jfl ' '

poo

§jj^

д;

интеграл J —^^^ при a > 0 сходится.

г) Сравним подынтегральную функцию

/w=

2хЧ7й-1?

с функцией

(р{х)

—.

Найдем предел их

отношения

,. 2x'+x^{x-\f ..

lim h= = lim

2 +

1 1

x'"

;c-»~

i^i , 3/4

Зх^+^/х'+г

Vx X

/•oo ^2X

Поскольку — расходится, то на основании второго при-

•'i X

знака сходимости несобственных интегралов расходится

дан-

ный интеграл.

608

Гпава 11

д)

Пользуясь признаком

Дирихле,

полагаем f{x) =

i^""

sin 2х,

(р (х)

—^.

Функция -^ -^

при

оо,

монотонно

убывая.

Де-

лая замену

= sinx, |х =

0, Г

x =

Z?,

sinZ>|,

получим

е""'' sin lxdx\

psinb

Интегрируя по частям, будем иметь

ръ\г\Ъ , I , isin Ъ

te'dtUl\eit-\\

<2е.

Т.

е. интеграл от функции /(х) ограничен.

Поскольку условия признака Дирихле выполнены, то дан-

ный интеграл сходится.

6.4. Исследовать сходимость интегралов: а) | . ;

г! dx

Inx

б) f -^; в) [ .

г) f4nsinxd!x; д) Г—r-^Jx.

Решение, а)

точке х =

подынтегральная функция имеет

разрыв, т. е. обращается в бесконечность. Разложим подкорен-

ное выражение на множители

1 1 11

л/х'-1 л/(^~1)(х

1)(хЧ1) л/^7(^ + 1)(хЧ1)

1 1 1

Отсюда, при

будем иметь

77^^27^'

Так как интеграл

р2 dx _ - с2

Ji 1

d-^\jp

^->i

= 2

(х-\у

ОПРЕПЕПЕННЫЙ ИНТЕГРАП 609

СХОДИТСЯ,

то данный интеграл также сходится.

б) В точке

X = 1

подынтегральная функция имеет разрыв.

Найдем предел отношения подынтегральной функции и функ-

ции

(р(х)

JC-1

.. 1пх ^

lim = 1.

Поскольку порядок подынтегральной функции по отноше-

нию к функции равен единице (а =

1),

то данный интеграл

JC-1

расходится.

в) В точке х

0 подынтегральная функция имеет разрыв.

Поскольку

^Х --Х X , _-JC

,. е -е ., е +е .

lim = lim = 2,

х-^О

X ^^0 1

то порядок подынтегральной функции относительно — равен

2 . ^

= —

<\. Следовательно, данный интеграл сходится.

г) В точке

подынтегральная функция имеет разрыв.

Воспользуемся интегрированием по

частям.

Полагая

sin

jc,

cos X

dx\ du = dx, v

x, получим

sinjc

f7i • T 1 • I- fT cosjc ,

c^^xdx

Mlnsinxax: = jclnsmjc2 - ^x dx

-\^ .

Jo 10 Jo gjj^^ Jo tgX

X X

Поскольку lim =

и lim =0 , то последний ин-

-^+ngx

x-.|-otgx

теграл является собственным. Следовательно, данный интеграл

сходится.