Черненко В.Д. Высшая математика в примерах и задачах (том 1)
Подождите немного. Документ загружается.


540 Гпава 10
—, , где ^.(0 —полином степени и.
\At''
+
Bt
+
су •^А.е +
B,t
+ С,
Приравнивая коэффициенты Л и 5, нулю, получим урав-
нения B
=
la^
+
p{a
+
fi)-\-2q
=
Q\
B^=2aap+bia
+
|i)
+
2c
=
0
для определения вещественных значений а и р .
При этом интеграл представляется суммой интегралов двух
видов:
1
{Af^-\-Cy.jA,t^+C,
И
t /it
J , 7 . ;
(^
=
0,1,2,...),
\At^
+
Cy^A,t'
+
C,
которые интегрируются подстановками, соответственно,
A^t^
+
Q=u^ и A^+Q'^-^v^,
Если p
=
b
=
0,TO интеграл представляется суммой двух ин-
тегралов
xdx _г dx
(х^
-hqyyjax^+c
*'
(х^ +дУл1ах^+с '
которые находятся подстановками, соответственно, ах^ + с = i/^
и а +
сх~^
= v^.
r(5x-3)Jx f xflfx
5.1.
Найти интегралы: а) J^n^^Ti' б) ]зхЧ4;с + 5'
J:C&
. г х+3 ^ , Г-. f 2'dx
4-2"+2'
Решение, а) Выделим в знаменателе полный квадрат
{5x-3)dx _ г (5x-3)d:r
K--6x
+
9-l6~^
9-16 •'(х-3)'-16

НЕОПРЕПЕПЕННЫИ ИНТЕГРАП
541
И
сделаем замену х-Ъ-t, dx
=
dt, x
=
t
+
3,
тогда получим
•5^+12,
5rd(t^-\6)
dt 12
r^r+iz , э га(г -10) ,_f at J, \г .л i^ ,
Ч^-\6 V t^-ie
•'^'-4'
2 I ' 2-4
^-4
t+A\
+C--
= —Inbc^ -6д:-7 + —In
2 I I 2
x-1
Л-
+
1
+
C.
6) Выделим в знаменателе полный квадрат
1 f xdx 1 f xdx
3J 2 A 4 5
2—xH
h —
3 9 9 3
-w
34 2X 11
x +
- +
—
3 9
2 2
и сделаем замену x
+ — =
t, dx
=
dt, x
=
t —, тогда получим
3J 2 11 З-* 2 И 9''
9 9
dt
гЧ
^лт^^
V
у
Ль
6
r+-
11
2 3 3t ^
rarctg-F=+C =
9Vn
'ViT
=i,„
6
2 4 15
л:
+—x
+
—
3 9
2
3JC
+ 2 ^
arctg—f=r-+C.
3>/n
" Vn
B)
Выделим под корнем полный квадрат
г xdx с xdx
1
^-^ 2
-+2-+Х
4 2
=1-
'!
Г1
^"
-
+ х
2
1 J J 1
и сделаем замену x
+ —
= t, dx = dt, x = t—, тогда получим
2 2

542
Гпава 10
t \dt
tdt
dt
I-'
— t'
1 . 2t
—arcsm-7=- = -
2
VS
r'
5 г"! 1 .2?
ir'
—t
\
J
—arcsin -7= + С =
2 V5
:->/r:
7 1 . 2x +
l
^
x-x —arcsin—7=—hC
2
VS
r) Вьщелим под корнем полный квадрат
f (^
+ 3)
^^,_ f (х + ЗУх
•'Vx42x + 1-1 •'V(x
+
1)'-1
и сделаем замену х
+1
= /, dx
=
dt, x
=
t-\, тогда получим
+
С.
4ё^х
+21nL
+ V/^-l +С = л/х^+2;с + 21пх
+ 1 +
л/х^+2х
д) Выделим под корнем полный квадрат
Ух" -^lx
+ \-'Ъdx =
\^{x^\f -Zdx
и сделаем замену х
+1
= /, dx
=
dt, тогда получим J v/^ ~ 3 J/.
При нахождении данного интеграла воспользуемся обоб-
щенной формулой
(7.П.
10.1).
\4t'-3dt = -'^'^'
=
-(/л/?'-3-31п(^
+
л//'-з))
+с=
= -((х
+
1)л/л:'+2х-2-31п(х +
1 +
л/хЧ2х-2))+С.
е) Сделаем замену 2' = /,
2"
In
2dx = rf/, тогда получим

НЕОПРЕПЕПЕННЫИ ИНТЕГРАП
543
^ [ dt _ 1 f dt 1 г d{t-2)
•-2-V2
2^2
In
2
In
t-2 + y/2
+
C
=
2л/21п2
In
(/-2)
2"-2-л/2
2"-2 + л/2
+ C.
etc
6)
I
(х
+
1)л/х^
+
2х +
2'
5.2.
Найти интегралы: a) Г
dx
. f ,^ , f
Решение, a) Сделаем подстановку
x
+ l = -,
d!x
=
—j-,
тог-
да получим
J
dx
{x
+ l)^ix
+
\f
+
:-ln
i +
лЛч!
+ C = -ln
1
+ л/?+2х + 2
x +
1
+
C.
1 J ^^
6) Делаем замену x
=
-, ax
=
—^, получим
f ^ _ f ^^^ - ( dt _
2
•'(2^-1)^
2 ^ ^ ^ l^x J
—1 +C
1 1 J ^^
в)
Делаем замену x-l=-, dx = —^, тогда получим
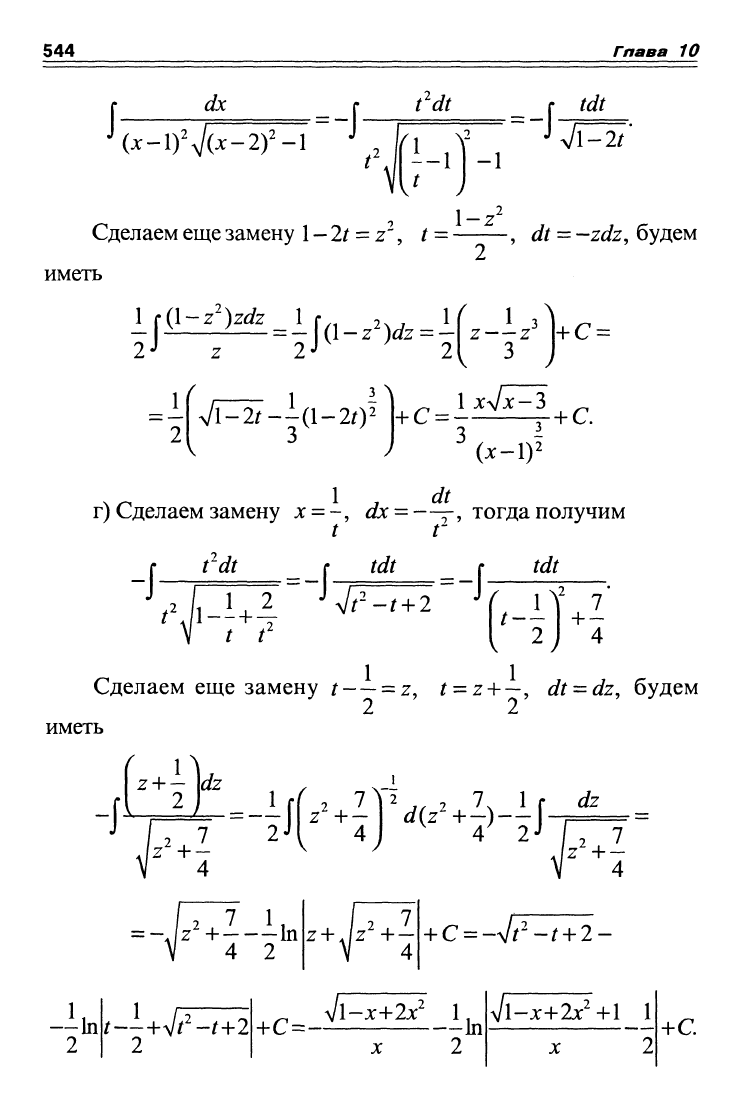
544
Гпава 10
I
dx
(x-l)V(x-2)^-1
-\-
t^dt
t\\\\-\y\
-J
tdt
yl\-2t'
Сделаем
еще
замену \-2t
=
z', t = , dt = -zdz, будем
иметь
ij(iz£V^aj„_..),4
2-
z
f 1 3^
z — z
V
+
C^
/
1
3 Ч
^jl-2t--{l-lty
3
+
C
=
у
1 Ху/Х — З
3 ^
+ C.
r) Сделаем замену x = -, d^ = —;-, тогда получим
t r
-J
rrf^
tdt
rc/r
.Ш ^v^
^ 2 Г4
Сделаем еще замену
f
—
=
z,
?
=
z +—,
dt
=
dz,
будем
иметь
f П
z
+
- Jz , '
fl 2 J 1 гГ 2 7V_,. 2 7, 1 г fife
.2.7 1
= -.z'+-—In
V 4 2
z
+
.
z"+-
V
4
•C = -^t^-t + 2-
-ii„
2
?—+л/Л^^7+2
2
^ Vl-x+2x^ 1,
+C= In
X 2
Vl-x+2x4l 1
+C.

НЕОПРЕПЕПЕННЫЙ ИНТЕГРАП 545
5.3.
Найти интеграл: а) / ^
==(ix\
6)
J
(lx
+
\)dx
(3JC^
+
4X
+ 4)л/д:^+6х-1
Решение, a) Воспользуемся формулой
(1),
тогда получим
f х^ + 4х , , , ^. п г г , tic
Vx^ + 2x + 2 yJx^+2x
+
2
Продифференцируем правую и левую часть
х^+4х
,
1—2—
г (Ах
+
А,)(х
+
\) А.,
+ 2х +
2
л/л:^
+ 2х + 2
Приведем к общему знаменателю и приравняем правую и
левую части
х^+4х
=
А^
(х^ + 2х + 2) + (А^х + Д
)(л:
+1)
+ Д.
Приравниваем неопределенные коэффициенты при одина-
ковых степенях неизвестных
X
1
=
А^
"1"
Д)?
х"
0 =
24^+4+^^2-
Решая данную систему уравнений, получим 4) = ~» ^' ~ о"'
7
Л - ~Т- Таким образом, интеграл примет вид
, dx
=
-{x
+
5Ux^
+
2x+2 , ' =
•'Vx42x + 2 2 2^(;с + 1)'+1
= -(х
+
5)^х^ +2х
+
2—lnx
+
l
+
Vx^
+
2jc
+ 2
2 2 I
+ С.

546
Гпава
10
б) Воспользуемся подстановкой х =
(^^
+ Р ^v-.^Zl
t + \
dx- ,dt.
тогда интеграл примет вид
•-\
(2х + \)dx
-\
(Зх^ +
4л:
+ 4)л/х^ +
6JC
-1
{7at+2p+t+\\a-p)dt
Приравнивая в квадратных трехчленах коэффициенты при
t к нулю, запишем систему уравнений относительно а, fi
6ai8 + 4(a + j8)+8 = 0,
2a^8
+ 6(a + j3)-2 = 0,
откуда а =
-1,
j8 = 2.
Интеграл в этом случае будет
{t-S)dt 1 г tdt
'-\
-^,\-.
•41;
dt
(?Ч8)л/15-6/' >/3-'(/Ч8)л/5-2/' л/з-'(^Ч8)л/5-2^'"
Первый интеграл находим с помощью подстановки
5-2t^=u^,
t^
=—(5-и^), tdt =
——udu,
тогда.
1_
2
tdt
-и
du
^\t'+S)yl5-2t'
S^2\-u' 6л/7
•In
м+>/21
м-л/2Т
+
С
=
6л/7
In
(«
+
N/21)'
« -21
+С=-
6л/7
In
(л/д:Чбл;-1+(д:+1)л/7)
д/4(Зд:Ч4д;+4)'
+С =
'зТ^
In
VX46JC-1+(JC+1)>/7
72(3x44x+4)
+
С.

НЕОПРЕПЕПЕННЫИ ИНТЕГРАП
547
Второй интеграл решаем посредством подстановки
-2
2
t 5 v'+2
, тогда
Jr
1 г t;42
Ar , ._ _ ^
4ъ\ещ45^ л/з-* 8^421 8л/з 8л/з
=:^1
Ju =
-
f/y
г au _
1 5 /8 ^
8N/3
48VI4
V21
л/хЧбх-1 5 л/8(х'+6х-1) ^
8(2-x) 48ч/14
Окончательно получим
(2-x)yFJ
, л/хЧбх-1 5 л/8(х'+6х-1)
8(2-х) 48Vl4 (2-x)V7
|VX' + 6X-1 + (X + 1)N/7
Зл/7
In
^2(Зх^+4х + 4)
+ C.
10*6.
Интегрирование рациональных дробей
1°.
Если подынтегральная функция представляет непра-
вильную рациональную дробь
aw
т.е.
т>п ,
то
следует
выделить целую часть делением числителя на знаменатель
«уголком». В этом случае дробь представляется в виде сум-
мы многочлена и правильной рациональной дроби, у кото-
рой степень числителя ниже степени знаменателя.

548
Гпава
10
Р
(jc)
2°.
Интегрирование правильной рациональной дроби -^—-,
aw
где т<п производится разложением ее на сумму простых все-
гда интегрируемых
дробей.
Для этого необходимо:
1.
Разложить знаменатель
Q^
(х) на простейшие множите-
ли,
причем могут встретиться следующие случаи:
а) корни знаменателя действительны и различны;
б) корни знаменателя действительные и некоторые из них
кратные;
в) среди корней знаменателя есть комплексные;
г) среди корней знаменателя есть комплексные кратные.
В общем случае разложение имеет вид
Q^{x)
=
a^{x-aY'
... {x-bfix^-^px
+
qf- ...
(jc'+CJC
+t/V,
где m,«,A:,/ =
l,2,3,
... ; а^,а,Ь,р,д,с,с1— постоянные, причем
p^-4q<0,
c^-4d<0.
2.
Написать схему разложения данной дроби на сумму про-
стых дробей
Р(х) А А, А^ В, В„
-Jnl^
= L_4- 1-—+ ... + ^ + L_+ ... + +
QSx) х-а (jc-a)' {x-af x^-b
(x-b)"
, M,x
+
N,
^^^^
^ M,x
+
N, ^ C,x
+
D,
^^^^^ дх
+
Ц
x^+px
+
q '" (x^+px-^-qY x^+cx
+
d '" (x^+cx
+
dy'
где
A^^A^,
... ,Л^^Р -
.^и.^Р
- ^^k^ ^P - '
^k^C^^
- ' Q'
Д, ..., Д — некоторые неопределенные постоянные. Для каж-
дого множителя в разложении знаменателя
Q^
(jc) выписывает-
ся столько простых дробей, какова его кратность (т,п,к,1).
Знаменателями простых дробей являются целые степени каждо-
го множителя, начиная с первого и кончая той степенью, кото-
рую множитель имеет в разложении.

НЕОПРЕПЕПЕННЫЙ ИНТЕГРАП 549
3.
Освободиться от знаменателей, умножая обе части ра-
венства на
Q^
{х).
4.
Составить систему уравнений, сравнивая коэффициенты
при одинаковых степенях х в обеих частях тождества (метод нео-
пределенных коэффициентов). Число уравнений должно быть
равно числу неопределенных коэффициентов.
5.
Решить систему и подставить найденные значения нео-
пределенных коэффициентов Д,
5j,
Мр
TVp Ср
Д, ...
в
схему раз-
ложения.
Неопределенные коэффициенты можно найти, если поло-
жить
X
в разложении равным действительным значениям корней
знаменателя Q^ix) или подходяще выбранным числам. При ре-
шении некоторых примеров этот метод определения коэффици-
ентов целесообразно комбинировать
с
методом неопределенных
коэффициентов.
3°.
Метод Остроградского. Если многочлен
Q^
(jc) имеет
кратные корни, то справедлива формула
'Qs^)
Qw •'aw
где Q (x) — наибольший общий делитель многочлена
Q^
(JC)
И
его производной Q[{x)\ 62W определяется делением
Qni^)
I
Q\i^)'^
Р\{^\ ^W—многочлены
с
неопределенными ко-
эффициентами, у которых степени на единицу меньше, соответ-
ственно, степеней Q(jc) и Qjix).
Дифференцируя формулу Остроградского, представим ее в
виде
aw
Q^{x)
aw
Для определения неопределенных коэффициентов
