Черненко В.Д. Высшая математика в примерах и задачах (том 1)
Подождите немного. Документ загружается.


560
Гпава
10
\ f dx \ f dx _
Пх' -6л:
-20JC423X'
-2X-1 1
{x-\)\x
+
\f
1
+-ln
6
6x-l
x
+ \
+
C.
10.7*
Интегралы от иррациональных функций
Интегралы от иррациональных функций берутся только в
некоторых частных случаях. Основным приемом интегрирова-
ния является отыскание таких подстановок, которые приводят
подынтегральное выражение к рациональному виду.
1°.
Интегралы вида i?(jc,jc"',
JC"'
, ... )dx, где R — некото-
рая рациональная функция;
т^^т^.п^.п^
— целые числа, приво-
дятся к интегралу от рациональной функции с помощью
подстановки х =
Л'
dx
=
kt^'^dt,
где к — общий знаменатель
дробных показателей.
2^.
Интегралы более общего вида
или
1^
х,\
ах
+ь Т
cx + d
f ax + b
\^
cx + d
\dx
приводятся к рациональному виду
с
помощью аналогичных под-
k ax + b k , ^ ^
становок ax
+ b =
t ,
=
t , где/:— общий знаменатель
cx + d
дробей а,j8, ....
3°.
Интеграл от дифференциального бинома
jx'"{a-}-bx"ydx
,
где т,
п,
р,а,Ь — постоянные числа, преобра-
зуется с помощью подстановки x=z
"
к виду
— [z'^^a +
bzY dz.

НЕОПРЕПЕПЕННЫЙ ИНТЕГРАП бб^
где q =
1
и приводится к интегралу от рациональной фун-
п
кции в следующих трех случаях:
1.
Если р — целое, то подстановка z = /"', где щ — знаме-
натель дроби ^ = —^.
щ
2.
Если целое, то и
1
— тоже целое
и
подста-
п п
171
новка а
+
Ьх"
=a
+
bz
=
t"', где
Щ
— знаменатель дроби р
=
—^.
3.
Если \-р — целое число, то p
+
q =
1 +
р —
п п
с fa
+
bzY
тоже целое и интеграл равен \z^{a
+
bzY dz = z^^^ dz.
Интеграл приводится к интегралу от рациональной функции
подстановкой ах +Ь
= =
t \ где
п^
— знаменатель дро-
Z
би р = —^.
4''.
Интегрирование выражений вида R(x,yjax^+Ьх-\-с)'
Подстановки Эйлера.
1.
Если а >
О,
тогдал/ох^+Ьх +
с
=t-yjax , откуда
I—2—;
yfat^
+Ы
+
сл/а
г- , Ыах +bjc + c= 7= ,
2yjat
+
b 2yjat
+
b
х =
е-с
, ^yfat^-hbt
+ cyja
.
dx - 2 р= dt,
{24at^bf
2.Если
с >
О,
тогда ыах^
-^Ьх + с
=xt
+ yjc
, откуда
2y[at-b I—2—] yfct^-bt
+ yfc
JC
= :;—, У/ах +bx + C= ; ,
a-r a-r

562
Гпава
10
ax
—
2 r—; at.
{a-ef
3.
Если квадратный трехчлен ax^+bx
+
c имеет различные
вещественные корни,т. е.
ах^+6X
+
C
= (2(X-A)(JC-/I), тогда
л1с1Х^
-hbx +
c
=
t{x -
Я),
откуда
t^-a Г-а '
Замечание. При а >
О,
с >
О,
т. е. в первой и второй подста-
новках можно было бы положить, соответственно,
yjax^
-i-bx + c
=^ + vax , vox^ +bx
+
c =
хГ
- vc
. В
третьей подста-
новке
yjax^
+
ЬхЛ-с=1{х-11)- Следует заметить, что в большин-
стве случаев подстановки Эйлера приводят к более длинным
вычислениям, чем другие методы.
5°.
Интегралы вида \R{x,
yJAx^
+
Вх^
+
Сх^
+ Dx
+
E)dx, где
R — рациональная функция, называемые эллиптическими, во-
обще говоря не интегрируются,
если
между коэффициентами фун-
кции R или полинома под знаком радикала нет особых
соотношений.
В
ряде случаев, при наличии возвратных полино-
1
мов,
интеграл находится с помощью подстановок х +
—
=
^
или
X
1
X
= t .
X
7.1.
Найти интегралы: а) | i^dx; б) xv3-xJx;
•'х + л/х -^
^) \ I 7 зГ^^ ^)
\~\Г~^^^'^
Д) \'. Г УГ="*
^
л/х
+
1+л/х +
1
^
X
VX-1
-^ 1
+ л/х +
л/1
+ х

НЕОПРЕПЕПЕННЫИ ИНТЕГРАП
563
Решение, а) Общий знаменатель дробных показателей сте-
пеней равен четырем, поэтому делаем замену x
—
t^, dx
=
At^dt.
Отсюда
\
+ t
1 +
^—
j=dx =Л\-—-rdt
=
A\-—dt
=
A
Vx+-ln(Vx + l)-arctg^
dt =
+
C
=
= 4
+
C.
6) Чтобы избавиться от радикала, сделаем замену 3-x
=
t^,
x-3-t^, dx
=
-Itdt,
тогда получим
J л:л/з^й!х =-2 J
(3
-/'V'Jf =
=
-2\(bt^-t^)dt
=
-2
t'-^t'
+ C =
— {b-xf\x
+
2)
+
C.
в) Общий знаменатель дробных показателей равен шести,
поэтому делаем замену x
+
\
=
t^;
dx
=
6t^dt.
Отсюда
r-t+i—
1
/+i
\dt^
=
6
+r-ln
? + l
,32 '
V
+ C = 6
/
-y[x
+ l
л/х
+ \
+
3 2
+ л/х+Т-1пк/х + 1+1
+ C.
/
г) Чтобы избавиться от радикала, сделаем замену
х
+ 1
•
t ; х-
; dx--
Atdt
(,'-i)
J, тогда получим

564 Гпава 10
-J dx
=
-4\- -dt
=
-4\— r
Представим подынтегральную функцию в виде суммы двух
более простых дробей
с
неопределенными коэффициентами
А В
Г
(г'+!)(/'-1) /41 t^-l
r=At-A
+
Bt+B;
{l
=
A
+
B, 0
=
-А
+
В}^^ А
=—;
В =—, таким образом
= -2
1,
arctg/
+—In
t-l
t
+ l
+
C
=
x-l
2arctgJ hln
Vx + l
;-Vx'-l
\+C.
д) Умножим числитель и знаменатель на
^Jl +
x -
(1
+ л[х),
тогда будем иметь
[
-1^-^-^
^^
[^^^'^-^^
dx
=
-\x\x + -\dx-
h
+
x-(l
+
^f J -2л/1 2J 2J
— IJ
dx =
4x+—x— [J dx.
гЦ X 2 in X
r
1
+ x
Рассмотрим dx
=
I отдельно. Сделаем замену
1 + X 2
=r, jc
X
t4t
e-\
, Jx
Itdt
('=-')
Интеграл примет вид
J n,c t at
^ ~ "^J 71—7ТГ
•
Подынтегральную функцию представим в виде
суммы двух более простых дробей
At-^B Ct^D
(^ -ir {t-\y
(r + 1)
2 •

НЕОПРЕПЕПЕННЫЙ ИНТЕГРАЛ
565
Приравниваем числители
t" = {At + Е){е + 2/ +1) + (а + D)(/' -
2/
+1)
и неопределеные коэффициенты при одинаковых степенях t
t^
Q
=
A
+ C,
t^ l = 2A + B-2C + D,
t 0 =
A
+ 2B + C-2D,
/" 0 =
B
+ D.
Решая данную систему уравнений, находим: А =—, В
=
0,
1 4
С = —, £) = 0.
4
Отсюда
\ г tdt \ г tdt \(( dt г, ,._2,
Л
1 = — Z-+- 7 = — + (^-1) «^ +
f—-[(?
+ !)-'f/H=-(-ln|/-l|
+
-!-+ln If+
l|
+—+C
=
Jf+l J J 2 ' ' /-1 ' ' f+1
+ ^—+С = lnl/x +
yjl
+
x\
+ yj x(l + x) + С
1
+—
2
2
Таким образом, окончательно получим
f r= i=== = -ix + 2yJ^-\n\^fx +
yJl'\'x\--Jx(\
+ x)] + C.
П +
Л[Х
+
УП
+ Х 2V I I ^ /
dx
6)
J
7.2. Найти интегралы:
^)1
r;
B) j-
л/;с(1
+ ^х)''
Решение, a) Подынтегральное выражение представляет
диф-
ференциальный бином. р
= —2
— целое число, поэтому приме-
няем подстановку
д;
= г", dx
=
4t^dt.
Интеграл примет вид
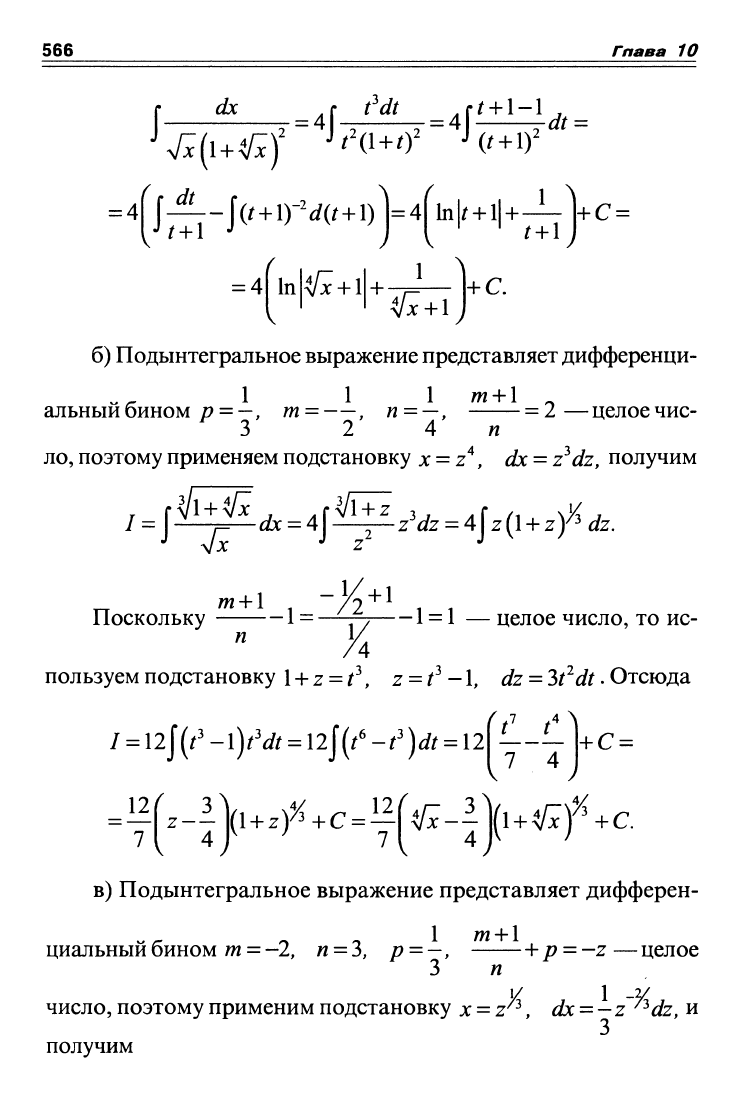
566 Гпава 10
•t+\-\
(1+0^
4t+\y
dt =
ink+il+— +c=
f +
1
l+c.
6) Подынтегральное выражение представляет дифференци-
111
т
+
\
^
альныибином р =
—,
т-—, п-—, -2—целоечис-
3 2 4 и
ло,
поэтому применяем подстановку x
=
z*, dx
=
z^dz, получим
I
=
f:!l^dx^A\^z4z
=
^\z{\^z)y^z.
Поскольку
m
+
1
-1 =
-
z
-1/+1
-1 =
1
— целое число, то ис-
пользуем подстановку
1
ч-
z = /^ z =
/^ -1,
dz
=
3t^dt
-
Отсюда
7 4
1+С
=
/ = 12j(/'-l)fV/ = 12j(/'-^')^ = 12
=H(z-|)(i.z)«.c=f(</:?-i)(i.</jf.c.
в) Подынтегральное выражение представляет дифферен-
^ ^ 1
/w
+ l
циальныи бином
m
=
-2,
« =
3,
/? =
—,
+/? = -z
—
целое
3
Д2
!/ 1 -У
число, поэтому применим подстановку x
=
z^^, dx
=—z^^dz,H
получим

НЕОПРЕПЕПЕННЫИ ИНТЕГРАП
567
•-\
dx
-к
%л
••¥>
^-\\ A'-^Yd..
Интеграл приводится к интегралу от рациональной функ-
ции
с
помощью подстановки
1
+
Z
=
t\
z
=
1
t'-\
,
dz
_3£dt_
(,'-if
'4i'4r'-^4^^-lf-l^'=
1
/
=
--t
+
C =
—
2t^
2
1
+ z
1
+ z
+
C
=
^,3
^
l
+
jc'
V
a)
I
dx
6)
J
jcMjc +
Vx^flJ
7.3.
Найти интегралы:
dx . f
3JC~-5X
у
;
в)
J , =dx.
Решение,
a)
Воспользуемся первой подстановкой Эйлера
д:
+l
= r-x.
Возводя в квадрат, получим
х
=
,
dx = —^ dt.
Подставляя под знак интеграла, будем иметь
'=1
dx
JC^(X+VJ?+1)
=1-
(^4lVf
^41
2^^
/,2_1Л'
2/
/.2
2
,
1
\
Г-1
Г+1
2/
2/
= 2[^
Г^^
f(r-ir
Воспользуемся методом Остроградского. Представим
подынтегральную функцию в виде

568
Гпава 10
_L±L
t{r-\f
At
+
B
С Dt
+
E
+—+•
t
e-\
Найдем производную, приведем к общему знаменателю и
приравняем коэффициенты
при
одинаковых
степенях
неизвестных
f"
0
=
С +
Д
t^ 0
=
-А
+
Е,
i" \
=
-lB-lC-D,
t 0
=
-А-Е,
f \
=
С.
Отсюда: А
=
0,
В
=
-\, С
=
\, D
=
-\, Е
=
0.
Интеграл при-
мет вид
/ = 2 — + \- =2 In , — +C.
Переходя к переменной x, окончательно будем иметь
/
2
In
x
+
Vx^hl
\
2JC
V
:(jc
+
Vx^+lJ
+
C.
6) Воспользуемся второй подстановкой Эйлера
2^
+
1
V^^-^ +
l
=/^ +
1.
Возводя в квадрат, получим х-
1~Г
2 '
^ ^г+Г +
1
, п 7
dx-L
T-rdt,
sx ~jc +
l
=
знак интеграла, будем иметь
dx
r +
r
+
1
„
;—. Подставляя все это под
1-Г
Г+/
+
1
-dt.
•'x + Vx^-x
+ l
J(^'-l)(/'+3f + 2)
Воспользуемся методом неопределенных коэффициентов:

НЕОПРЕШЕПЕННЫЙ ИНТЕГРАП
569
r+f+i
В
D
{t'-\)it'+2>t + 2)
t-\
t +
\
{t + \y t + 2
f4f + l = ^r + 2)(^42/ + l) + 5(? + 2)(r'-l) +
+C{t
-
\){t +
2)
+ D{t +1)(/' -1),
t^ 0 =
A
+
B
+ D,
t^ \ =
AA
+ 2B +
C-\-D,
t l = 5A-B + C-D,
f" l = 2A-2B-2C-D.
1
3 5
Отсюда A
=
—,B
= —,
C
=
-l, D
=
—. Таким образом:
6
2 3
/=_if^_зf-^+2f-A_ч-l^f^=
3J/-1 J t
+ l
Ht
+ ^)
3-'/ + 2
=—ln|f-l|-31nlf +
l|
+—lni/ +
2|
+
C.
3
' ' ' ' f+1 3 ' '
Переходя к переменной x, получим
|-31n
/ = —
InNx^
-x +
l-l-x\
3
I
+101n
yJx'^-x
+
\-l
+
2x\
yjx^
-x
+
l-l
+
x\
2x
+
C.
yjx^
-x
+ \
-l
+ jc
в) Поскольку подкоренное выражение имеет два действи-
тельных корня, то воспользуемся третьей подстановкой Эйлера
\J3-2x-x =(3 + x)t, откуда х= ^
, ,
ах =
-
Интеграл примет вид
3x'-5x
^
=
1-
.dx
=
4l
l + t'
1
+
4/'-2к'
(\+ty
Ь-2х-х'
•'
(f'+l)'
Воспользуемся методом Остроградского
dt.
