Черненко В.Д. Высшая математика в примерах и задачах (том 1)
Подождите немного. Документ загружается.


90 Гпава 2
2°.
Свойства.
1.
При перестановке сомножителей смешанное произведе-
ние меняет знак
(ax6)c--ffexaVc=(5xc)-6
=-(схб)а.
(2)
2.
Смешанное произведение обладает свойством
(ахб)с=(^хс)й = (схй)6. (3)
3.
Если два из трех векторов равны или параллельны, то их
смешанное произведение равно нулю.
3°.
Смешанное произведение трех векторов численно равно
объему параллелепипеда, построенного на этих векторах
К = (йх^)с=56с. (4)
4°.
Объем пирамиды, построенной на векторах 5,6,
с
равен
^п=;^(йхб)с=1а6с. (5)
5°.
Условие компланарности. Необходимым
и
достаточным
условием компланарности трех векторов 5,6,
с
является равен-
ство нулю их смешанного произведения:
аЪс =
О.
5.1.
В пространстве даны четыре точки: А (1,1,1),
В (2,4,7),С (-1,2,-3), и D (-3,2,1). Найти объем тетраэдра ^5CZ)
и длину высоты тетраэдра, опуш[енной из вершины В.
Решение. Пусть А вершина тетрэдра. Найдем координаты
векторов 1в, JC и ~AD (рис. 2.19): А5 =
{1,3,6},
АС
=
{-2,1,-4},
AD =
{-4,1,0}.
Объем тетраэдра находим по
формуле (5)
I
1 3 б|
-2 1 -^
М 1 О
6
32
3 •

ВЕКТОРНАЯ АПГЕБРА
91
Рис. 2.19
Найдем площадь основания
S = ACxAD\
'г
1 к\
-2 1 -4
-Л 1 0
1
[i
—»
~*
Ai+\ej
+
2k\
769.
, 3F ,3-32 32л/б9
Поскольку
А
= —, то
А
= —р= = .
S Зл/б9 69
5.2.
Вычислить объем треугольной призмы, построенной на
векторах
й{1,-3,2},
fc
{3,1,-2},
с
{2,-1,2},
и определить ори-
ентацию тройки векторов й, 6,
с
в пространстве.
Решение. Найдем значение смешанного произведения
а{Ьхс\
=
1 -3 2
3 1 -2
2-12
=
20.
Поскольку смешанное произведение векторов положитель-
ное,
то они образуют правую тройку.
Объем треугольной призмы равен половине объема парал-
лелепипеда построенного на этих векторах

92
Гпава 2
5.3.
Доказать компланарность векторов
й{4,3,5},
б{2,2,2},
с{~3,-2,-4}
Решение. Условие компланарности а = 0. Откуда
I
4 3 5|
й(^хс)= 2 2 2 =0,
|-3 -2 -41
следовательно, векторы компланарны.
5.4. Даны векторы а =
(-1,-1,2)
и 6 = (1,-2,2). Найти неиз-
вестный вектор x = (x,y,z), если скалярное произведение
5
• Зс
= -7
5
вектор с =ахх перпендикулярен оси Ох, а смешан-
ное произведение хаЬ = 2.
Решение. Используя условие а-х
= —1 •>
получим уравнение
-x-j^
+ 2z= -7 или x
+
;;-2z = 7.
Воспользуемся векторным произведением
с =ахх
^ J
-1 -1
X
У
'{z
+
2y)I
+
(2x
+
z)]
+
{x-y)k,
Поскольку вектор с перпендикулярен оси Ох, то проекция
с^ вектора с на ось Ох равна
О,
то есть
с^=
-
{2y+z)
= 0.
Из условия хаЬ
=
2 имеем
X у z
1-1 -1 2
1 -2 2
:2,
т.е. 2x +
4>;
+ 3z = 2.

ВЕКТОРНАЯ АПГЕБРА
93
Полученные уравнения объединим
в
систему
x-\-y
—
2z
=
l,
ly
+
z
=
0,
[2х+Ау+Ъ2
=
2.
Решение ищем по формулам Крамера. Находим определи-
тель системы
D
=
1 1 -2
О 2 1
2 4 3
= 12^0.
Так как определитель системы не равен нулю, то система
А ^у А
имеет единственное решение х
=
^, у
=
—^, z = —^.
D =
7 1
0 2
2 4
-2
1
3
=
24:
Д.
1 7
0 0
2 2
-2'
1
3
12;
D =
1
0
2
1 7
2 0
4 2
= -24;
24 ^ 12 , -24 ^
jc
= — = 2, v= — =
1,
z = = -2.
12 12 12
Таким образом, неизвестный вектор х
=
{2,1,
-2} .
5.5.
На векторах d
=
2i-\-j-k,
b=3J-2j
+
4k и
с=ЗТ -4k построен параллелепипед. Найти его высоту, опу-
щенную на грань, образованную векторами due.
Решение. Объем параллелепипеда по формуле (4) будет
=
116 +
12-6
+ 121
= 34.
2 1-1
Г = |й6с|= 3 -2 41
II3
0-41
С другой стороны, объем равен V
=
S- h, где S
-
площадь
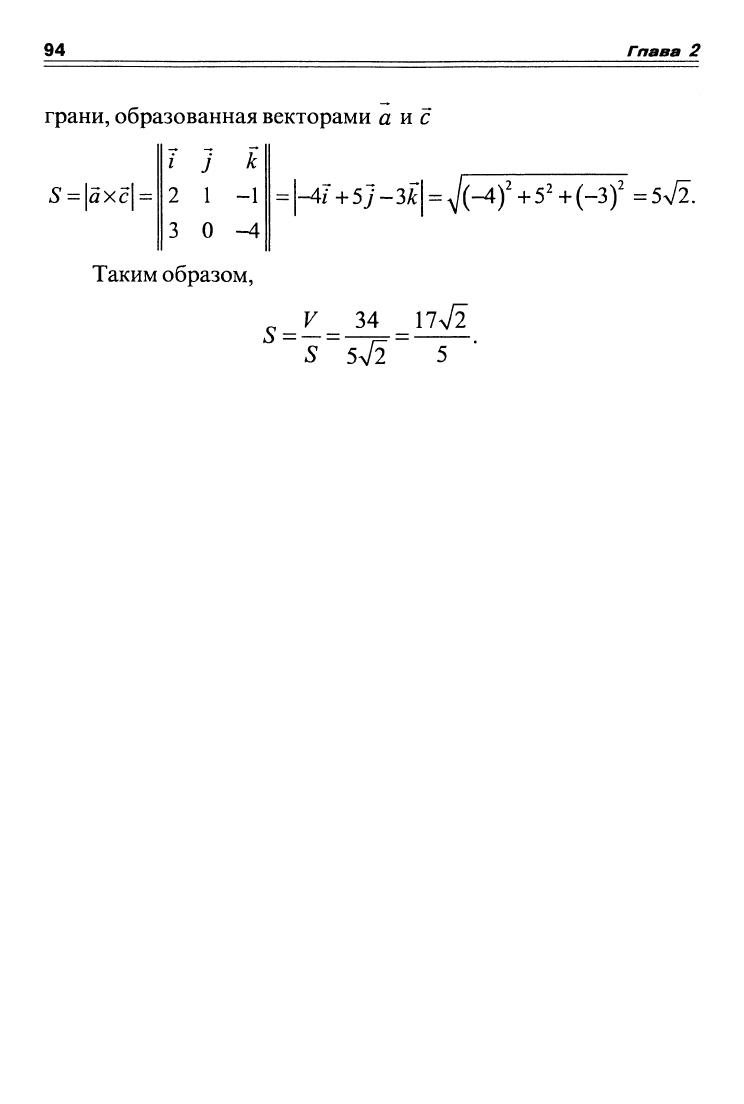
94
Гпава
2
грани,
образованная векторами
а и с
5
=
|йхс|
=
2 1 -1
3 0 ^
=
-4Г
+
57
-
3it|
= J(-4)'+
5'+ (-3)'
Таким
образом,
s
=
F_
34
_llsl2
5~5V2~
5
= 572.

Глава 3
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
НА ПЛОСКОСТИ
3.1.
Координаты точки на прямой
и на плоскости. Длина и направление отрезка
1°.
Координатой
точки М на оси х называется положитель-
ное или отрицательное
число,
отложенное, соответственно, впра-
во или влево от начала координат в выбранном масштабе.
Декартова или
прямоугольная система координат
представ-
ляет совокупность двух взаимно-перпендикулярных осей; оси
абсцисс Ох и оси ординат Оу (рис. 3.1).
Щ^гУ^
Рис. 3.1

96 Гпава 3
Декартовыми координатами точки М называются проекции
радиус-вектора ОМ на оси координат
(х,>^).
Направленным отрезком на оси называется отрезок, у ко-
торого определены начало Mj(Xj) и конец М^х^. Здесь
х^^.х^
—
координаты начала и конца отрезка.
2°.
Величина отрезка на оси равна его длине
М^М^\М^М^,
если направление отрезка совпадает с осью; в противном слу-
чае величина отрезка равна его длине со знаком минус
MyJ\df^-\M^M^,
Через координаты величина отрезка опреде-
ляется по формуле
Му^М^х^-х^^ (1)
а длина или расстояние между двумя точками
t/=MiM2=|jC2-JCi|. (2)
Длина отрезка на плоскости (рис. 3.1), заданного коорди-
натами своего начала Mj(xj,jj) и конца М^х^.у^ , равна
^
=
7(Хз-х,)Ч(>;,-д;,)^
(3)
Если начало отрезка совпадает с началом координат, то
формула (3) примет вид
d=4777.
(4)
3°.
Пусть (р и у/ — углы, составляемые отрезком с по-
ложительными направлениями осей координат Ох, Оу, тог-
да направление отрезка определится заданием косинусов этих
углов
cosy
=
-7= ^ ^ ; cosii/=—j= ^ ^ (^\
V(x, -x,f НУг -УхУ
V(^2
-^i)' НУг 'УхУ ^ ^
1.1. Построить на числовой оси точки ^4(-4), В{5), и С(1),
найти величины отрезков АВ,ВС и АС
яз,
оси,
длину отрезка ВС
и проверить равенство
АВ-^ВС-АС,

АНАПИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ППОСКОСТИ 97
Решение. На оси х в выбранном масштабе откладываем от
начала координат соответственно точки А,В
и
С (рис
.3.2).
Вели-
чины отрезков находим по формуле (1)
В
-4 0 1 5
Рис. 3.2
АВ = Хв-х^=5-(-4) =
9,
ВС = Хс-Хд=1-5=-4,
АС = Хс-х^=1-(-4) = 5.
Длину отрезка ВС находим по формуле (2)
d = \BC\=\x^-x,\=\-4\=4.
Подставляя найденные величины отрезков на оси
в
доказы-
ваемое равенство, получим 9+(-4)=5, 5=5.
1.2. Даны точки А{-1,-3) и В{4,2), Найти длину отрезка и
его направление.
Решение. Длину отрезка, заданного координатами своего
начала и конца находим по формуле (3)
^=|^5|=7(4 + 1)'+(2 + 3)'=л/50=5л/2.
Направляющие косинусы находим по формулам (5)
4 +
1
1 л/2
2
+
3
V2
Отсюда угол
с
положительным направлением оси Ох равен
(р = 45°, а оси Оу равен у/ =
45"".
1.3. Найти точку, удаленную от оси Оу и от точки ^4(1,2) на
5 единиц.
Решение. Геометрическим местом точек удаленных от оси
Оу и точки А будет прямая параллельная оси Оу и отстоящая от

98
Гпава 3
ОСИ
на расстоянии 5 единиц (рис. 3.3), т. е. х = 5. Пусть точка
M(5,j^) искомая точка, тогда по формуле (3)
5 =
7(5^4)40^'
откуда 25=16+(у-2)2 или (у-2)2=9.
У \
о
А{1.2)
Н 1 1 h-
м.
м.
Рис. 3.3
Решая последнее уравнение, находим у^=5,
^2""^-
Таким
образом, искомых точек на прямой две Mj(5,5), М2(5,-1).
1.4. Найти центр и радиус окружности, описанной около
треугольника с вершинами ^(2,1), Д-3,2), С(-1,1).
Решение. Обозначим координаты центра окружности О за
X,
у, а радиус за
i?,
тогда по формуле (3) будем иметь
R'={x-2f+(y-l)\
К'={х
+
ЗУ+{у-2)\
R'={x
+
lf+(y-^\)\
1
Вычитая из первого третье уравнение, находим, что ^ ~ т
•
1
Подставляя ^ =
—
во второе и третье и вычитая из второго тре-
^ 13
тье,
находим, что У~'^- Подставляя найденные х,у
в
любое из
трех уравнений, получаем, что R =
л/Гзо
1.5. Доказать, что четырехугольник с вершинами в точках
У4(1,5),
5(-2,1), С(1,-2), и Z)(10,2) есть параллелограмм.

АНАПИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ППОСКОСТИ 99
Решение. Известно, что четырехугольник, у которого про-
тивоположные стороны попарно равны, есть параллелограмм.
Докажем равенство противоположных сторон АВ и CD (ВС и
DA).
Найдем длины этих сторон
Следовательно, АВ
=
CD.
Аналогично: d^^
=
V(7 + 2)'+(-2~1)' = Зл/ш ,
dj,^=yl{l-lOf+i5-2f =3VlO,ToecTb BC
=
DA.
Поскольку противоположные стороны равны, то четыре-
хугольник ABCD есть параллелограмм, что и требовалось до-
казать.
3.2. Деление отрезка в данном отношении.
Площадь треугольника и многоугольника.
Центр тяжести
l"". Координаты точки М(х,у), делящей отрезок М^М^ в от-
ношении —^— =
Я
, (рис. 3.1) находятся по формулам
JC,
+
Хх^
у, + Я v^
х
=
- -\ у
= —
— (1)
1
+
Я
-^
1
+
Я
• ^^
Если точка М делит отрезок М^М^ пополам, то Я =
1
и ко-
ординаты равны
X
4-
х^
V, +
у-у
^=^у^;
У=^^^-
(2)
Если Я — число отрицательное, то точка М находится на
продолжении отрезка М^М^
и
деление называется внешним.
