Цейтлин Н.А. Из опыта аналитического статистика
Подождите немного. Документ загружается.

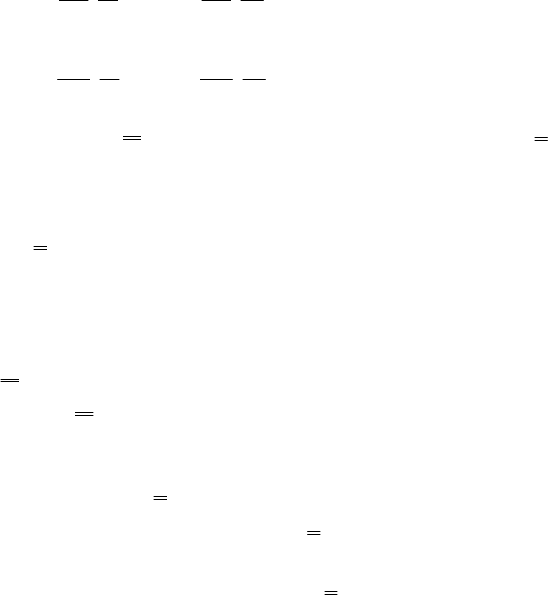
7
(
)
(
)
()()
=
nnn
n
YXYX
YXYX
H
~
,...
~
,
.........
~
,...
~
,
1
111
(1.14)
были ортогональны.
Таким образом, ортогональность плана X недостаточна для ортогональности плана Y .
Необходимо, чтобы выполнялось также условие ортогональности столбцов матрицы Н. Данное
условие не является тривиальным и может быть удовлетворено в редких случаях, только при
определенном классе зависимостей переменных Y
i
от факторов X
i
, независимо от усилий
исследователя. Поскольку матрица Y - случайная, то гипотезу о ее ортогональности можно
сформулировать, например, как статистическую гипотезу о не значимости максимального
значения абсолютной величины выборочного коэффициента корреляции [6].
В такой ситуации для построения "плана" эксперимента, близкого к оптимальному,
предлагается следующая итерационная процедура:
1) строится ортогональный план X эксперимента для независимых переменных X
i
;
2) выполняются эксперименты по плану X ;
3) строятся прямые (1.4) и обратные(1.5) функции регрессии;
4) проверяется адекватность построенных моделей;
5) выполняется анализ близости матрицы "плана" Y к оптимальной для моделей (1.5);
6) если модели (1.4) и (1.5) адекватны и матрица "плана" Y оказывается близкой к
оптимальной, процедура считается законченной;
7) если модели (1.4) и (1.5) не адекватны, или матрица "плана" Y неудовлетворительна,
следует достроить ее до близкой к оптимальной и, воспользовавшись обратными моделями
(1.5), вычислить соответствующие значения переменных X
i
. Затем вернуться к пункту 2).
Достройка плана по переменным Y
i
может осуществляться с применением специального
программного обеспечения ПЭВМ [7].
9.1.4. Наличие одной существенной и ряда менее существенных переменных в моделях.
Априори известно [2], что наиболее существенное влияние на зависимые переменные Y
i
в
формулах (1.4) и X
i
в формулах (1.5) оказывают одноименные независимые переменные X
i
и Y
i
соответственно. Менее существенным является влияние разноименных переменных. При большом
диапазоне варьирования факторов возможно также менее существенное, но все же статистически
значимое влияние на зависимые переменные квадратичных эффектов и эффектов взаимодействия
независимых переменным. Так, например, в градуировочную функцию (1.5) квадратичные
эффекты могут войти в виде
α
ii
Y
i
Y
i
, эффекты взаимодействия - в виде парных
α
ij
Y
i
Y
j
, тройных
α
ijk
Y
i
Y
j
Y
k
и т. д. эффектов.
В настоящее время нет достаточного количества экспериментальных данных, которые
позволили бы судить, насколько большим является диапазон варьирования факторов и,
следовательно, какого порядка (первого или второго) план эксперимента следует использовать.
Это обстоятельство затрудняет выбор порядка плана в различных ситуациях. В общем случае
можно рекомендовать стратегию последовательного планирования эксперимента [5]. Сначала
составляется план первого порядка - ПФЭ, или ДФЭ с рядом параллельных опытов в центре
плана. По параллельным опытам оценивается дисперсия воспроизводимости отклика Y,
проверяется адекватность полученных моделей (1.4) и (1,5) по остаточным дисперсиям (обе
модели) и по сумме квадратичных эффектов (
ii
β
Σ
= 0) - для модели (1.4). Априори известно, что в
сумме
ii
β
Σ
наиболее существенным является параметр
β
ii
, индексы которого совпадают с
индексом отклика; остальные параметры
β
jj
можно считать равными нулю. Поэтому если
окажется, что
ii
β
Σ
≠
0, то план достраивается до плана второго порядка путем добавления всего

8
по 2 опыта по каждому фактору X
i
в звездных точках [5]. Опять проверяется адекватность обеих
моделей.
Необходимость построения моделей порядка выше второго, как показывает опыт авторов [3,
4], маловероятна.
По мере накопления данных и построения градуировочных функций (1.5) можно ставить
вопрос о том, каков должен быть диапазон варьирования факторов, чтобы для аппроксимации
градуировочной функции можно было использовать планы и модели первого или второго
порядка.
9.1.5. Оценивание параметров в обратной задаче регрессионного анализа.
9.1.5.1. Взаимно однозначное отображение области определения в область значений
градуировочной функции.
Для того чтобы принципиально было возможно построение обратного оператора (1.2),
ставящего в соответствие вектору
Y
вектор
X
, необходимо и достаточно, чтобы прямой
оператор (1.1), ставящий в соответствие вектору
X
вектор
Y
, осуществлял взаимно однозначное
отображение своей области определения в область значений [8]. Это значит, что для нелинейной
системы (1.1) следует ограничиться такой областью факторного пространства, на которой
функция отклика Y ( X ) удовлетворила бы указанному условию. Очевидно, данное условие
выполнено для линейных моделей на всем факторном пространстве. Но уже при наличии
попарных произведений (в модели (1.5)
β
ij
≠
0) возможна неоднозначность. Значит, в ходе
исследования реальных данных следует построить прямые функции регрессии и убедиться в том,
что условие взаимной однозначности на исследуемой области имеет место. Следует ожидать, что
данный прием допустим, так как область исследования в данном случае представляет собой
малую окрестность нуля (Z << 1). Это же обстоятельство позволяет предположить, что искомая
поверхность на исследуемой области концентраций может быть аппроксимирована, в основном, с
помощью главных эффектов и немногих эффектов взаимодействия невысокого порядка.
9.1.5.2. Проблемы оценивания параметров обратных регрессионных моделей.
Хотя отклики моделей (1.5) - суть переменные не стохастические, процедура оценивания
коэффициентов функций регрессии требует таких данных, которые уменьшили бы дисперсию
предсказания отклика и смещение самих коэффициентов регрессии. Действительно, рассмотрим
для простоты линейную модель
0
1
n
ii
i
XCCY
=
=+
∑
. (1.15)
Так как каждый регрессор Y
i
имеет некую ошибку Е
i
и детерминированную составляющую
МY
i
, эту модель можно переписать в виде
0
11
nn
iiii
ii
XCCMYCE
==
=++
∑∑
. (1.16)
Если случайные величины Е
i
распределены по нормальному закону, то величина
ii
ECE
=Σ
распределена тоже по нормальному закону. Для линейной модели все предположения
регрессионного анализа сохраняются при переходе от прямой задачи к обратной, и, следова-
тельно, необходимо составить план эксперимента, обладающий оптимальными свойствами. Если
обратная модель имеет более высокий порядок, случайная составляющая войдет в нее не только в
виде аддитивной добавки, но и в произведениях с факторами. Такие модели относятся к классу
нелинейных моделей. Для оценивания параметров нелинейных моделей принято минимизировать
функционалы [9]
()
()
(
)
2
2
222
11
nn
iijiiXikjkjYk
jk
SXCgYYYσσ
−−
==
=−+−
∑∑
,
(1.17)
где
2
Xi
σ
,
2
Yi
σ
- дисперсии переменных X
i
, Y
k
;
kj
Y
- значение переменной Y
k
в j-ом опыте, заданное
в плане эксперимента; X
ij
, Y
kj
- измеренные значения переменных X
i
, Y
k
в j-ом опыте. В случае,
если Y
k
– переменные, относительно которых можно непосредственно составить план
эксперимента, такой подход возможен. Однако в нашем случае план для переменных Y
k
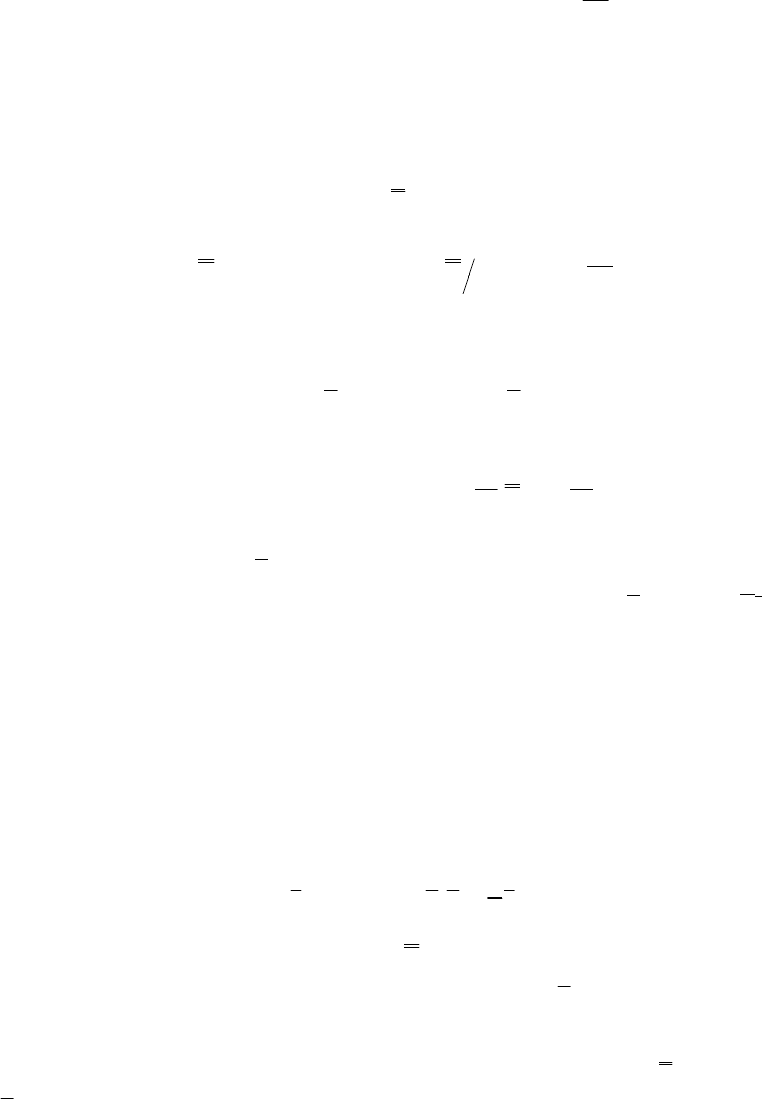
9
составляется опосредованно через планы для переменных X
k
( nk ,1= ). Это делает невозможным
минимизацию второго слагаемого, стоящего под знаком суммы, и задача сводится к оценке
коэффициентов регрессии С
i
методом наименьшие квадратов.
9.1.5.3. Интервальная оценка результата измерений.
Согласно требованиям ГОСТа [11], кроме точечных оценок результатов измерений (1.5)
необходимо выполнять их интервальные оценки. Доверительный интервал с заранее заданной
высокой доверительной вероятностью
p−1
для результатов Y
i
измерения выражается
формулой
(
)
npXXp
BiiHi
−=<< 1
ˆˆ
ϑ ;
1,,
in
= (1.18)
где
Hi
X
ˆ
,
Bi
X
ˆ
- нижняя и верхняя границы доверительного интервала;
i
ϑ
- истинное значение
результата (косвенного) измерения концентрации элемента i.
В свою очередь,
(
)
ˆˆ
;
Hiii
XXYX
=−∆
(
)
ˆˆ
,
Biii
XXYX
=+∆
где
i
X
∆
– полуразмах
доверительного интервала;
(){}
(
)
5.0
0
1
0
2/;
′
′
∗=∆
−
YYYYSnpftX
xii
, (1.20)
где t{.} - верхний р/(2n) - предел распределение Стьюдента с f степенями свободы; S
xi
- оценка СО
ошибки расчета величины X
i
;
0
Y
- вектор измеренных значений интенсивностей линий спектров
всей группы элементов, используемых в градуировочной функции
(
)
YX
i
ˆ
. Вектор Y
0
является
аргументом функций (1.20).
1.5.4. Определение величины смещения оценок параметров градуировочной функции.
При планировании градуировочного эксперимента возможна установка факторов Х
i
с
пренебрежимо малой погрешностью, так что факторы Х
i
в плане можно считать
детерминированными управляемыми величинами. Наличие ряда параллельных опытов в плане
позволяет оценить дисперсии (
Yi
σ
)
2
ошибок Е
i
откликов Y
i
[5]. Использование обычного метода
наименьших квадратов для оценки коэффициентов моделей (1.4) и (1.5) приведет к несмещенным
оценкам b
i
→
β
i
модели (1.4) и смещенным оценкам а
i
→
α
i
модели (1.5) [9]. Величина смещения
вектора коэффициентов оценивается по формуле [9]
()
aQYYpna
1
1
−
′
−−=∆ , (1.21)
где р - число коэффициентов регрессии (1.5); Q - диагональная матрица дисперсий переменных
Y
i
,
(
)
22
2
2
1
,...,,,0
YnYY
diagD σσσ=
. Величина смещения
a
∆
тем больше, чем ближе к
вырожденной матрица
Y
Y
′
. При достаточно малых значениях дисперсий
2
Yi
σ погрешностей
измерения интенсивностей Y
i
и близкой к ортогональной матрице "плана" Y величина смешения
a
∆
оказывается несущественно малой.
9.1.5.5. Структурная идентификация градуировочной функции.
Существует большое количество формул различной структуры для аппроксимации
градуировочной функции [2]. В настоящей работе используются эмпирические формулы (1.4) и
(1.5), линейные по оцениваемым коэффициентам. Такая структура облегчает задачу оптимального
планирования градуировочного эксперимента. После завершения экспериментов приступают к
расчету коэффициентов регрессии и проверки гипотез об их значимом отличии от нуля [5].
Значимые коэффициенты оставляют в градуировочной формуле, незначимые исключают из нее.
Полученные градуировочные функции со всеми значимыми коэффициентами проверяют на
адекватность.

10
При обращении к программе регрессионного анализа [6] невозможно сразу определить,
какие требования адекватности могут возникнуть в будущем. Поэтому приходится наряду с
лучшей, наиболее точной ГФ, получать ряд менее точных с меньшим числом значимых членов
ГФ.
Выбор между сложными или простыми, точными или грубыми ГФ является предметом
экспертной оценки.
9.1.5.6. Распределение суммарной погрешности результатов измерения МВИ.
При аттестации МВИ [11, 23] большое внимание уделяется выбору правдоподобной
аппроксимации функции распределения плотности вероятностей погрешности измерения. На
погрешность определения концентраций компонентов исследуемых МВИ оказывает влияние
много разных факторов. Так, погрешность воспроизводимости отклика Y
j
зависит от
погрешностей установления факторов X
i
на заданных уровнях, погрешностей измерения отклика
и вариации факторов, не учтенных в плане эксперимента. Последние две погрешности разделить
трудно. Их природа может быть обусловлена неравномерностью распределения на образце массы
солей элементов, выкристаллизовавшихся из раствора, неравномерностью интенсивности
рентгеновского излучения, вариацией тока и напряжения в рентгеновской трубке, неточностью
установки образца в фокусе прибора, наличием посторонних примесей на стеклянной посуде, в
воздухе, на фильтровальной бумаге, неточностью определения объема дозируемого раствора,
вариацией температуры помещения, различия в опытности и аккуратности лаборантов и тому
подобными причинами.
Это позволяет предполагать, что наиболее правдоподобной является аппроксимация
распределения суммарной погрешности нормальным законом. Для проверки гипотезы о
нормальном распределении погрешности при малом объеме выборки 50 > N > 15 рекомендуется
применять
α
- критерий Фишера [Р2.5], предложенный в работе [10]. При большом объеме
выборки, N > 50 наиболее мощным является критерий Мизеса-Смирнова-Крамера [22; Р2.5].
9.1.6. Необходимость одновременной проверки ряда различных статистических гипотез.
Проверка различных статистических гипотез в данной работе осуществляется альфа-
методом [10, Р1]. Если альтернативная гипотеза Н
1
является дизъюнкцией l частных независимых
альтернативных гипотез Н
1i
,
li ,1=
, то оценку уровня значимости вычисляют по формуле [10]
{
}
i
l
α
α
ˆ
min
ˆ
1
=
, (или
l
i
)
ˆ
min1(1
ˆ
1
αα −−=
при
3
.
0
ˆ
>
α
). (1.22)
Оценки
i
α
ˆ
могут вычисляться с помощью функций надежности распределения различных
проверочных статистик. Если
i
α
ˆ
попадает в критическую область (
k
α
α
<
ˆ
), то нулевая гипотеза
Н
0
отклоняется, если – в допустимую
k
α
α
≥
ˆ
, то не отклоняется.
Отметим, что таблицу [Т2Р1] можно использовать для выбора доверительной вероятности
1-
k
α
, необходимой при интервальном оценивании параметров [2]. Статистические оценки
параметров должны быть надежными. Это требование соответствует предпочтению
альтернативной гипотезы. С увеличением ответственности за выводы интервальные оценки
получаются более широкими.
9.1.7. Проверка адекватности системы градуировочных функций.
9.1.7.1. Первичная обработка данных.
Исходные данные для первичной обработки представляют собой nN групп
{
}
j
K
l
j
il
Y
1=
замеров интенсивностей линий спектра n элементов i в K
j
параллельных опытах в N точках плана
( Njni ,1;,1 == ). При планировании градуировочного эксперимента используются три типа
планов: (а) - план с параллельными опытами только в последнем, N-ом опыте в центре плана, то
есть K
j
= 1 для 1,1 −= Nj и K
N
> 1; (б) - план с одинаковым числом m > 1 опытов во всех
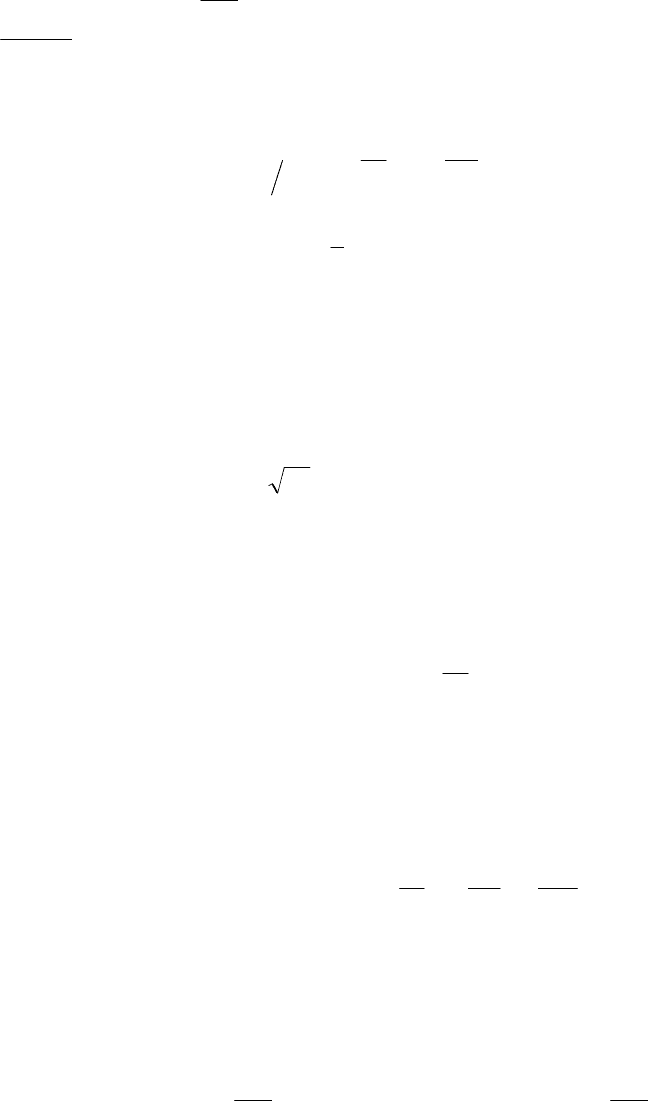
11
точках плана, то есть K
j
= m для Nj ,1= и (в) - план типа (а), повторенный 2 или 3 раза, то есть
K
j
= m для 1,1 −= Nj и K
N
> m и m = 2 или 3.
Задачи первичной обработки данных следующие:
(1) выявление и исправление выбросов - грубых ошибок эксперимента;
(3) вычисление средних значений интенсивностей линий спектра элементов в точках плана
.
1
,1,;1,
j
K
ijiljj
l
YYKinjN
=
===
∑
; (1.23)
(3) вычисление СО ошибок воспроизводимости в группах параллельных опытов
()
()
0,5
2
1
/1
j
K
ij
ijiljj
l
SYYK
=
=−−
∑
(1.24)
с ЧСС, равным f
j
= K
j
– 1.
Замечание. На практике может случайно встретиться группа с одинаковыми значениями
измеренных переменных. В этом случае оценка СО (1.24) даёт неверный результат (ноль),
противоречащий физическому смыслу. (Кроме того, дальнейшее использование этого результата в
формуле (1.28) приводит к сбою в работе программы, так как деление на ноль невозможно).
Поэтому таком случае вместо оценки СО (1.24) рекомендуется [Р1.1.12.2] использовать оценку СО
для равномерного распределения
ijijij
LLS 3.012/ ≈= , где L
ij
- единица последнего разряда
значащих цифр одинаковых чисел. Например, если все три (К
j
= 3) значения Y
ilj
равны 712 (1/с), то
L
ij
= 1 (1/с) и S
ij
= 0.3 (1/с).
(4) проверка гипотез об однородности оценок S
ij
СО;
(5) вычисление средневзвешенных оценок СО воспроизводимости откликов Y
i
путём
усреднения однородных оценок S
ij
СО,
()()
0.5
2
11
1/1,1,
NN
восYiijjj
jj
SSKKin
==
=−−=
∑∑
(1.25)
с ЧСС, равным
(
)
1
вос jj
jj
ffK
==−
∑∑
(в формулах (1.23) - (1.25) 1 < К
j
<
∞
).
Грубые ошибки измерения оказывают существенное влияние на точность расчёта средних и
СО величин. Обычно задача исправления грубых ошибок уверенно решается экспертами сразу по
мере получения данных. Если эксперты сомневаются в наличии выброса, то используются
статистические процедуры.
Для экспертной оценки грубых ошибок составляется таблица размахов Q
ij
данных в группах,
{
}
{
}
jilj
l
ilj
l
ij
KlNjniYYQ ,1;,1;,1;minmax
∈
=
=
−
=
. (1.26)
Некоторые из размахов Q
ij
могут оказаться слишком большими. В группе данных,
характеризующихся подозрительно большим, по мнению экспертов, размахом, находят
выскакивающее значение и исправляют его путём проведения дополнительного опыта, или (что
хуже) - путём винсоризации [6], то есть замены выскакивающего значения на ближайшее из этой
же группы (см. также раздел 2.3.).
В практике проведения многофакторного градуировочного эксперимента по планам любого
типа может встретиться грубая ошибка, связанная с путаницей номеров строк плана эксперимента
(когда результаты опытов Y
ilj
строки Nj ,1∈ записываются в другую строку jgNg ≠∈ ,,1 ).
Опыт показывает, что интенсивность линий спектра Y
i
элемента i при определённой
концентрации X
i
элемента i в растворе незначительно колеблется вокруг некоторого среднего
значения при изменении концентрации остальных элементов в плане. Если же концентрация X
i
изменяется (в планах величина X
i
обычно изменяется на трёх уровнях,
{
}
++
∈
iii
XXX ;2/;0
), то
разброс интенсивностей Y
i
линий спектра элемента i становится существенным.
Основываясь на этих наблюдениях, можно для выявления путаницы номеров строк
плана эксперимента воспользоваться следующим, специфическим для градуировочного
эксперимента, приёмом. Необходимо собрать в три отдельные группы средние значения
12
интенсивностей Y
ij
линий i-го элемента, соответствующие трём одинаковым концентрациям X
i
этого элемента в растворе. Далее с помощью размахов (1.26), или критерия выбросов (например,
Смирнова-Груббса [6]) определить выскакивающее значение. Если после обсуждения экспертами
выскакивающее значение считается грубой ошибкой, соответствующие опыты повторяют.
Статистические процедуры определения выбросов в группах данных можно совместить с
решением остальных задач первичной обработки. Тактика первичной статистической обработки
данных градуировочного эксперимента зависит от типа используемого плана.
При использовании плана типа (а) анализируется только группа параллельных опытов в
центре плана с помощью какого-либо статистического критерия выбросов (например, Смирнова-
Груббса [6]). При отсутствии выбросов принимают S
восYi
= S
iN
, ni ,1= .
При использовании планов типа (б) и (в) задача (1) непосредственного определения грубых
ошибок в одной (или нескольких) группе данных статистическими методами становится очень
сложной. Однако, учитывая дальнейшую схему статистической обработки данных, задачу (1)
можно решать одновременно с задачей (4) проверки гипотез об однородности СО S
ij
в группах
данных. При использовании планов типа (б) подлежащие проверке нулевые гипотезы имеют вид
{
}
{
}
NjniH
ij
j
ij
j
ii
,1;,1;1min/max:
22
0
==== σσϕ , (1.27)
где
22
ijij
S→σ , против альтернатив Н
1i
:
ϕ
i
> 1 (см. гипотезу № 20
[
Т3Р1
]
).
Для проверки гипотез (1.27) используется критерий Фишера-Бонферрони (предложенный
нами в 1984 г. [10]). Вычисляется статистика критерия [Ф(51)Р1]
{
}
{
}
{
}
NjniSSffF
ij
j
ij
j
Fii
,1;,1;minmax
ˆ
,,
ˆ
22
===α , (1.28)
где f = (m – 1) - ЧСС СО S
ij;
α
Fi
- оценка уровня значимости для F-распределения.
По таблицам распределения Фишера [12], или по номограммам этого распределения [15;
рис. 5Р1], или по аппроксимирующим формулам [10; Ф(11), (14) и (16)Р1.2.2] при известных
значениях чисел степеней свободы числителя (f) и знаменателя (f) фишеровского отношения и
значению статистики
i
F
ˆ
(1.28) определяется первый сомножитель
Fi
α
ˆ
(равный
j
min
α
ij
)
формулы (1.22).
Если число m параллельных опытов во всех точках плана равно 2 или 3, то ЧСС
фишеровского отношения f равны 1 или 2 соответственно. В этих частных случаях используются
простые аппроксимации [10]
(
)
{
}
FiiFi
Farctg απα
ˆ
,1,1
ˆ
21
ˆ
5.0
−=
; (1.29)
{}
(
)
1
1
ˆ
,2,2
ˆ
ˆ
−
+=
FiiFi
F αα . (1.30)
Второй сомножитель формулы (1.22) равен [10] l = N ( N - 1 ). Тогда
(
)
Fii
NN
α
α
ˆ
1
ˆ
−
=
(или
(
)
(
)
1
ˆ
11
ˆ
−
−−=
NN
Fii
αα при 3.0
ˆ
>
i
α
). (1.31)
Полученные по формулам (1.31) значения
i
α
ˆ
сравниваются с критическим
α
k
. Если
ki
α
α
>
ˆ
, нулевые гипотезы Н
0i
(1.27) не отклоняются. Это позволяет перейти к шагу (5) -
усреднению всех однородных СО S
ij
по формуле (1.25). Если
ki
α
α
<
ˆ
, одна из нулевых гипотез
отклоняется.
В группе опытов, характеризующейся значимо большим СО, находят выброс и исправляют
его (путём повторения опыта, или винсоризацией).
При использовании планов типа (в) получаются N - 1 СО S
ij
с числами степеней свободы,
равными f = m - 1 и одно СО S
ij
с большим числом степеней свободы f
N
= K
N
– 1 > f. Поэтому
нулевые гипотезы Н
0i
об однородности всех СО сформулируем как конъюнкцию двух гипотез Н
01i
об однородности СО S
ij
с равными f ЧСС и гипотез H
02i
об однородности СО S
iN
с ЧСС f
N
и
среднего значения СО,
13
()
0.5
1
2
1
/1
N
i
ij
j
SSN
−
=
=−
∑
→
2
i
σ
[
()
1
22
1
/1
N
iij
j
Nσσ
−
=
=−
∑
] (1.32)
с ЧСС, равным f ( N - 1 ), рассчитанному по СО S
ij
, 1,1 −= Nj , упомянутым выше:
I
iii
HHH
02010
:
; ni ,1= ; (1.33)
{
}
{
}
1min/max:
22
01
==
′
ij
j
ij
j
ii
H σσϕ ; 1,1 −= Nj ; (1.34)
{
}
{
}
1,min/,max:
2222
02
==
′
Nii
j
Nii
j
i
H σσσσϕ . (1.35)
Соответствующие альтернативные гипотезы имеют вид
U
iii
HHH
12111
: ; ni ,1= ;
1:
11
>
′
ii
H ϕ ; H
12
i
:
ψ
> 1.
Для проверки гипотез (1.33) рассчитывают: 1) - оценку уровня значимости
j
α
ˆ
по формуле
(1.22) при l = 2; 2) - оценки
i1
ˆ
α
для частных гипотез (1.34) определяют с помощью статистики
(1.28) критерия Фишера-Бонферрони, где 1,1 −= Nj и формулы (1.31); 3) - оценки
i2
ˆ
α
для
частных гипотез (1.35) определяются с помощью статистики Фишера
{}
{
}
{
}
2
2
2
2
2
,min/,max
ˆ
,,
ˆ
Ni
i
Ni
i
iзнч
SSSSffF =α , (1.36)
где ЧСС числителя f
ч
и знаменателя f
зн
F - отношения определяются соотношением между СО S
i
и
S
Ni
: f
ч
= f (N-1) и f
зн
= f
N
, если
Ni
i
SS
≥
, или f
ч
= f
N
и f
зн
= f (N – 1), если
Ni
i
SS < . Затем
определяется уровень значимости
i2
ˆ
α
[10, 12, 15]. Подстановка вычисленных переменных в
формулу (1.22) приводит к выражениям
{
}
iii 21
ˆ
,
ˆ
min2
ˆ
α
α
α
=
(или
{
}
(
)
2
21
ˆ
,
ˆ
min11
ˆ
iii
ααα −−= при 3.0
ˆ
>
i
α
). (1.37)
Если
α
i
>
α
k
, гипотезы Н
0i
(1.33) не отклоняются и переходят к шагу (б). Если
α
i
<
α
k
, одна
из гипотез (1.33) отклоняется; находят выброс в соответствующей группе опытов, характе-
ризующейся наибольшим СО S
ij
и исправляют его.
9.1.7.2. Адекватность ГФ погрешности результатов наблюдений.
Процедура установления адекватности модели (1.4) зависит от типа плана и структуры
модели. Если план был первого порядка с параллельными опытами в центре плана, а в структуре
модели (1.4) отсутствуют квадратичные эффекты
2
iii
Xβ , то процедура проверки адекватности
модели с номером i следующая.
Нулевые гипотезы Н
0j
являются конъюнкцией двух гипотез Н
01j
и Н
02j
. Гипотезы Н
0j
состоят
в том, что равны дисперсии остаточная
2
0Yj
σ и воспроизводимости
2
восYj
σ , альтернативные
гипотезы -
22
011
:
восYjYjj
H σσ > . Гипотезы Н
02j
состоят в равенстве нулю сумм коэффициентов
iij
i
β
∑
модели (1.4); альтернативные ей гипотезы
12
:0
jiij
i
H β
≠
∑
. Таким образом
I
jjj
HHH
02010
:
;
22
001
:
восYjYjj
H σσ =
;
02
:0
jiij
i
H β
=
∑
. (1.38)
При фиксированном элементе
{
}
1,
jn
∈
имеется 3 альтернативные гипотезы (H
11j
-
односторонняя и Н
12j
- двусторонняя). Поэтому, для проверки гипотезы Н
0j
следует рассчитывать
оценку уровня значимости
j
α
ˆ
по формуле (1.22) при l = 3. Оценки
ij
α
ˆ
уровней значимости для
проверки частных гипотез определяют следующим образом: 1)
j1
ˆ
α
- по функциям надёжности
распределения Фишера с ЧСС f
0
и f
вос
[5, 10] и F-отношению
{
}
22
010
/,,
восYjYjjвос
SSffF =α ; (1.39)

14
2)
j2
ˆ
α
- по функциям надёжности распределения Стьюдента [5, 10] с ЧСС f и t-отношению
{}
(
)
5.0
11
0
1
0
0
ˆ
2/,
ˆ
−
−−−
+−= NNSYYft
восYjj
j
вос
α , (1.40)
где
j
Y
0
ˆ
- оценка отклика в центре плана;
j
Y
0
- среднее значение параллельных опытов в центре
плана; N
0
- число параллельных опытов в центре плана; N - общее число опытов.
Если план был второго порядка, независимо от наличия в структуре модели (1.4)
квадратичных эффектов, в качестве гипотезы об адекватности рассматривают только одну
гипотезу о равенстве дисперсий
22
00
:
восYjYjj
H σσ = против
22
01
:
восYjYjj
H σσ > (1.41)
по всем N + N
3
+ N
0
опытам плана, включая N
3
опытов в звездных точках и N
0
параллельных
опытов в центре плана. Уровень значимости для проверки этой гипотезы находят по обратной
функции распределения Фишера, как было описано выше.
Гипотезу об адекватности модели (1.5) проверить сложней. Переменные Х
i
в выражениях
(1.5) являются функциями случайных величин Y
i
, дисперсии воспроизводимости которых
2
Yi
σ
оцениваются в эксперименте.
Допустим, остаточные дисперсии
2
0Xi
S
и коэффициенты а
i
→
α
i
функций (1.5) получены
методом наименьших квадратов. Если функции (1.5) рассматривать как формулы косвенного
измерения, то дисперсии
2
восXi
S
ошибок расчета концентраций X
i
можно вычислить по известной
формуле (в предположении о независимости ошибок Е
i
[5]:
(
)
2
22
1
/
n
восXiiij восYj
j
SXYYS
=
=∂∂
∑
, ni ,1= . (1.42)
Сравнение дисперсий воспроизводимости
2
восXi
S и остаточной
2
oXi
S с помощью критерия
Фишера [10] позволит проверить гипотезу об адекватности формул (1.5).
Другой способ проверки адекватности формул (1.5) основан на проверке гипотез (1.38). Для
оценки остаточных дисперсий по моделям (1.5) вычисляются невязки
ijij
YY −
ˆ
, где
ij
Y
ˆ
-
расчетные значения переменной Y
i
в точке X
j
, получаемые путем решения системы уравнений
(1.5); Y
ij
- опытные значения переменной Y
i
в точке X
j
.
9.1.7.3. Адекватность другим требованиям.
При проверке адекватности регрессионных моделей общепринято использование в качестве
величины сравнения дисперсии воспроизводимости
2
вос
σ
отклика [5]. С этой дисперсией
сравнивают остаточную дисперсию
2
ост
σ
модели, с ней же сравнивают разность значений отклика
в центре плана при проверке незначимости суммы квадратичных эффектов модели [5]. Однако для
удовлетворения этой величине сравнения часто приходится использовать громоздкие
градуировочные функции с большим количеством членов.
На практике может потребоваться адекватность ГФ менее жестким условиям, например, при
использовании в качестве единицы сравнения некоторой заранее заданной грубой дисперсии
погрешности
2
Г
σ
. Это позволяет использовать не громоздкие ГФ с небольшим количеством
членов. (При использовании статистических критериев следует учесть, что дисперсии
2
Г
σ
соответствует число степеней свободы f
Г
=
∞
).
Используемая в настоящем исследовании программа регрессионного анализа имеет
подпрограмму получения лучшей регрессионной модели методом серий [6]. Этот метод позволяет
получить ряд полезных функций регрессии, сложных и точных, или простых и грубых,
предъявляемых ЛПР как множество решений регрессионной задачи.
9.2. Методика. Оптимальное планирование градуировочного эксперимента и построение
градуировочной функции прибора для определения концентраций компонентов водного

15
раствора методом рентгенофлуоресцентного анализа
Проведенный в предыдущих разделах теоретический анализ особенностей задач
градуировочного эксперимента показал, что каждая такая задача нетривиальна и требует
для своего решения участия специалиста по математической теории эксперимента или
АСа.
Построение градуировочных функций измерительного прибора для контроля содержания
ряда тяжелых элементов в растворе осуществляется согласно следующей операторной схеме
где знаками "+" и "-" обозначены "да" и "нет" соответственно; буквами обозначены
следующие операторы:
А. Определяется объект исследования (сбросные воды промышленного предприятия,
ливневые стоки и т. п.). Определяется уровень ответственности за выводы и задаётся критическое
значение уровня значимости для проверки гипотез [Т2Р1].
Собираются данные (архивные или экспертные) о количестве (n), наименованиях
(
)
nii ,1=
и значениях концентраций определяемых элементов в пробах за длительный период времени.
Из собранных данных выделяются максимальные значения
+++
n
XXX ,...,,
21
концентраций
элементов. Эти значения являются верхними пределами уровней варьирования факторов X
i
(нижние пределы равны нулям) и характеризуют область
Ω
х
(1.22) определения градуировочных
функций (1.5).
Б. Строится оптимальный факторный план первого порядка
X
для оценки параметров
линейной модели (1.4) с параллельными опытами в центре плана. В точке плана с нулевыми
концентрациями всех компонентов рекомендуется выполнить 10-20 опытов [5].
При числе факторов n < 5 используют ПФЭ 2
n
; при n > 5 используют дробные реплики
ФЭ 2
n-q
. Дробность 2
-q
реплики определяют, исходя из важности соотношений между
требованиями к точности градуировочных функций и стоимости (длительности) опытов. Если
априори известно, что ГФ аппроксимируются полиномами второго порядка, то необходимо
использовать наиболее экономные (по числу опытов) некомпозиционные планы второго порядка
[24, 25]. В более сложных случаях, когда ГФ по одним элементам аппроксимируются полиномами
первого порядка, а по другим - второго, приходится использовать разноуровневые планы [25].
В. Выполняют эксперименты по плану. Последовательность экспериментов рандомизируют
во времени [5].
Г. Осуществляют первичную обработку данных. Если в данных отсутствуют грубые ошибки
(см. знак «-» на схеме), обработка результатов наблюдений продолжается (п. Д). Если грубые
ошибки обнаружены (знак «+»), соответствующий опыт повторяют (или винсоризируют выброс) с
переходом к оператору В.
Д. Методом регрессионного анализа вычисляются оценки параметров моделей (1.4) и (1.5).
Е. Проверяются гипотезы (1.38) или (1.41) об адекватности моделей (1.4) и (1.5).
Ж. В случае неадекватности формулы для компонента i план эксперимента достраивается
до плана более высокого порядка по соответствующему фактору X
i
с переходом к оператору В.
И. Проверяется гипотеза о близости матрицы Y "плана" к ортогональной [6].
К. Если эта гипотеза отклоняется, "план" Y достраивается до близкого к ортогональному
путем добавления 1-й – 2-х точек
i
Y [7] и с помощью формулы (1.5) вычисляются значения
планируемых факторов X
i
с переходом к оператору В.
Л. (Если гипотезы об адекватности моделей (1.4) и (1.5) и ортогональности матрицы Y не
отклоняются.) Выводятся формулы (1.20) для интервальной оценки результатов косвенного
16
измерения концентраций элементов и процедура построения градуировочных функций
завершается.
9.3. Метрологическая аттестация методики выполнения измерений содержания
элементов в пробах растворов
Метрологическую аттестацию методики выполнения измерений (МВИ) необходимо
выполнять в соответствии с требованиями ГОСТа 8.505-84 [11, 23]. В этом ГОСТе описаны общие
положения, порядок проведения метрологической аттестации МВИ, требования к содержанию
технического отчета о метрологической аттестации МВИ, способы выражения показателей
точности измерений, выполняемых по МВИ, содержание документов на методики приготовления
смесей, применяемых для метрологической аттестации МВИ. Поэтому на этих вопросах
останавливаться не будем. Попытаемся осветить вопросы, специфические для рассматриваемой
задачи.
9.3.1. Определение объемов выборок.
Определению подлежат числа N контрольных растворов и m контрольных замеров в
каждой точке. Эта задача является предметом экспертной оценки. На выбор чисел N и m влияют:
трудоемкость, стоимость и длительность опытов, с одной стороны, необходимость получения
представительной выборки - с другой.
Представительной является выборка, имеющая случайный характер и большой объем.
Понятие "большой объем" невозможно определить четко. Для выбора ориентиров отметим, что
целью аттестации является проверка гипотезы о соответствии паспортных характеристик
погрешности МВИ наблюдаемым при аттестации данным. Такая проверка осуществляется с
применением статистического критерия Фишера [12].
Мощность критерия Фишера наиболее чувствительна к вариации чисел степеней свободы
знаменателя Фишеровского отношения. (Число степеней свободы оценки дисперсии, попадающей
в этот знаменатель, на единицу меньше соответствующего объема выборки).
С увеличением числа степеней свободы знаменателя Фишеровского отношения от 2 до 5
мощность критерия Фишера будет возрастать резко [12, с. 65]; в диапазоне чисел от 5 до 19 -
менее резко. Представление о "резком" и "менее резком" росте мощности является экспертным и в
данном случае отражает мнение автора. Из сказанного следует рекомендация считать объемы
выборок N и m в интервале от 6 до 20 - каждая достаточно большими.
9.3.2. Выбор координат контрольных точек плана метрологического эксперимента.
К моменту очередной метрологической аттестации МВИ накапливаются
экспериментальные данные о значениях концентраций определяемых компонентов в растворах
определенного класса (это могут быть сбросные воды предприятия, технологические растворы
химического цеха и т. п.). Наибольший интерес при аттестации МВИ может представить
определение его метрологических характеристик именно в отношении тех компонентов растворов
и в таких сочетаниях, которые чаще всего встречаются на практике (а не тех, которые были
использованы при построении градуировочной функции).
По этой причине для метрологической аттестации необходимо сделать случайную выборку
(объемом N единиц) из множества точек, встречавшихся в практике замера концентраций
элементов растворов определенного класса.
Процедура метрологической аттестации МВИ может быть использована не только для
проверки паспортных данных о погрешности МВИ, но и для коррекции (уточнения) ГФ МВИ. В
первом случае достаточно получение случайной выборки. Во втором случае (при заданных числах
N и m) можно воспользоваться вышеописанными методами планирования градуировочного
эксперимента для построения оптимального "плана" в пространстве откликов на области
Ω
Y
,
границы которой являются окаймлением области значений интенсивностей линий спектров
элементов, содержащихся в растворах определенного класса.
