Цейтлин Н.А. Из опыта аналитического статистика
Подождите немного. Документ загружается.

3
Экспериментальные точки были нанесены на графики в координатах γ - W; σ - [Cl]; σ - γ; σ - W;
точки соединяли отрезками прямых. Изучалась тенденция влияния факторов [Cl],
γ
и W на отклик
σ. Как и следовало ожидать, на уменьшение σ влияет повышение [Сl] и снижение γ и W. Три
точки, резко противоречащие наблюдаемым тенденциям, исключены как грубые ошибки опыта.
Оставшийся массив данных обрабатывали с помощью ЭВМ.
Обработка результатов наблюдений на ЭВМ. Трудности обработки результатов
наблюдений на ЭВМ заключались в том, что зависимость отклика σ в теоретической модели (1)
нелинейна по коэффициентам, а для оценивания коэффициентов пытались использовать
имеющеюся программу линейного регрессионного анализа [6].
Таблица 1.
Результаты экспериментального исследования смерзаемости известняковой муки
Результаты наблюдений Результаты расчетов
№ п/п
W [Cl]
γ
-t
σ
γ
н
σ
W
ˆ
-t
c
c
σ
ˆ
S
σ
f
σ
1 9 1 1,4 20 0,130
1,138 9.7 26,0
-0,42
0 5
2 9 1 1,5 28 0,653
1,138 9,7 24,8
0,35
0,22
2
3 9 1 1,6 20 1,000
1,138 9,7 23,6
0,51
0,10
2
4 9 1 1,6 28 0,914
1,138 9,7 23,6
0,82
0,12
2
5 9 1 1,7 20 1,807
1,138 9,7 22,5
0,98
0,81
2
… … … … … … … … … … … …
57 15 5 1,7 28 0,696
1,158 15,1
21,7
0,55
0,15
2
58 15 5 1,7 33 1,697
1,158 15,1
21,7
1,51
0,19
1
59 9 2 1,4 12 0 1,138 10,1
26,7
-1,40
* *
60 9 2 1,4 20 0 1,138 10,1
26,7
-0,79
* *
… … … … … … … … … … … …
152 15 5 1,7 12 0 1,158 15,1
21,7
-2,51
* *
153 15 5 1,7 20 0 1,158 15,1
21,7
-0,98
* *
*При σ = 0 значения S
σ
и f
σ
не определялись.
Сначала попытались упростить и линеаризовать исходную формулу (1). Положили
σ
т
= 0;
W
σ
= a
0
+ а
1
t
с
; t
c
= c
o
+c
1
[Сl] + c
2
γ
, где a
i
, с
i
– коэффициенты. Подставив эти выражения в (1) и
произведя элементарные преобразования, получили линейную по коэффициентам b
i
формулу
Y = σ
2
6
н
γ
/(W
2
γ
6
) = b
0
+ b
1
t + b
2
[Cl] + b
3
γ + b
4
W, (2)
где коэффициенты b
i
являются функциями коэффициентов а
i
и с
i
.
В обработку приняты 75 опытов, в которых σ > 0. Остаточное СО погрешности полученной
формулы оказалось очень большим - 8,2 кг/см
2
(поэтому формула не приведена). Причин
возникновения большой погрешности, по-видимому, две: первая - неудачная структура формулы
(2), вторая - неоднородность ошибок воспроизводимости отклика
σ
в опытах с непрочно и прочно
смерзшимися образцами. Поэтому для аппроксимации решили использовать полиномы второго
порядка, а для обработки взять опыты с непрочно смерзшимися образцами в окрестности зоны 0 <
σ
≤
4 кг/см
2
«повышенного интереса» - около точек
σ
= 0 и
σ
= 2 кг/см
2
. Значения W и t при
σ
= 0
принимают вид W
σ
и t
c
; значения
σ
= 2 кг/см
2
являются предельными при определении
необходимой массовой доли хлора [Сl]. Верхнее значение границы области (4 кг/см
2
) выбрано
потому, что более чем на два СО S
σ
н
= 0,44 кг/см
2
превышает значение σ = 2 кг/см
2
. В качестве
базисных функций приняли W, [Cl],
γ
, t,
σ
и
γ
н
и все возможные их парные произведения W
2
,
W[Cl], ..., σ
2
, σγ
н
,
2
н
γ .
Искали зависимости величин W, [Cl], t и
σ
от базисных функций, избранных так, чтобы
среди них не встречалась функция отклика. Например, при определении зависимости [Сl] от
базисных функций исключали [Сl]
2
, [Cl]W и т. д.

4
Расчеты выполняли с помощью программы линейного регрессионного анализа [6] на ЭВМ
ЕС-1045. Получили следующие эмпирические функции регрессии (ЭФР):
[
]
[
]
(
)
+
−+−+−+= ClClW
ннн
2
н
7,3737,4314,5203,604,4521,3576279,61
ˆ
γσγσγγ ; (3)
(
)
(
)
(
)
+
++−−−+−=
2
н
11720128,404812,0013737,03496,8 σγγσ бttWCl
; (4)
(
)
[
]
[
]
[
]
ClClWWClt γγγσ 708,21,1144993,09858,0673,1497,185
ˆ
2
н
−−+−+=−
; (5)
[
]
(
)
[
]
(
)
+
−
+
+
−
+
−
=
CltClWW 03843,013,412626,04425,01701,11
ˆ
нн
γγ
γ
σ
. (6)
(Напомним, что (U)
+
= 0, если U < 0, и (U)
+
= U, если U
≥
0).
Коэффициенты детерминации R
2
и регрессии полученных ЭФР высокозначимы (табл. 2).
(Коэффициенты детерминации R
2
характеризуют долю вариации отклика, обусловленную
вариацией учтенных в ЭФР факторов. Доля 1 - R
2
вариации отклика объясняется вариацией
неучтенных в ЭФР факторов).
Расчет технологических параметров при температуре смерзания. Температуру
смерзания смеси можно определить экспериментально. Однако для этой цели следовало
применить стратегию композиционного планирования оптимизационного эксперимента [5], что
привело бы к большим затратам времени.
Таблица 2.
Статистические характеристики эмпирических функций регрессии.
Номер формулы
СО остаточ-
ной ошибки S
o
Коэффициент
детерминации R
2
Уровни значимости коэффициентов
регрессии (по порядку)
(3) 0,8% 0,86
6
⋅
10
-8
; 10
-5
; 10
-3
; 10
-3
; 10
-3
; 10
-3
(4) 0,8% 0,71
6
⋅
10
-8
; 8
⋅
10
-6
; 5
⋅
10
-5
; 0,04
(5) 3,4 К 0,61 10
-6
; 10
-3
; 0,03; 0,04
(6) 0,65кг/см
2
0,61
6
⋅
10
-8
; 5
⋅
10
-7
; 3
⋅
10
-6
; 5
⋅
10
-5
В настоящей работе была использована стратегия некомпозиционного планирования: все
опыты провели сразу, а зависимость температуры смерзания от факторов нашли путем
экстраполяции зависимостей (3) и (5) в точку
σ
= 0.
Поскольку в результатах опытов, принятых в обработку, встречались точки со значениями
σ
> 0, близкими к нулю, то экстраполяцию полученных формул в точку
σ
= 0 считали допустимой.
Экстраполяция формул (3) и (5) в точку
σ
= 0 дала выражения для безопасной влажности W
σ
= W
ˆ
(γ
н
,[Сl] , σ = 0) и температуры смерзания t = t([Cl], W, v, γ, σ = 0). В свою очередь, подстановка
выражений W
σ
и t
c
в формулу (1) дала полуэмпирическую формулу для расчета
σ
.
Интерпретация полученных формул. Матрица плана эксперимента оказалась
мультиколлинеарной (
α
ˆ
< 10
-7
). Мультиколлинеарность плана объясняется тем, что в обработку
были приняты результаты не всех опытов, а лишь тех, для которых
σ
> 0. Поэтому, строго говоря,
интерпретация полученных ЭФР (то есть утверждение о влиянии каждого фактора в отдельности
на отклик по значениям коэффициентов регрессии) некорректна.
Попытаемся грубо оценить влияние наиболее важного фактора [Сl] на отклики в случае,
когда
σ
= 0. Выписав члены формулы (3), содержащие [Сl], получим а [Сl], где а = 43,37 - 37,7
γ
н
.
При минимальном значении
−
н
γ
= 1,138а = 0,47 > 0, а при максимальном
+
н
γ
= 1,158а = -0,29 < 0. С
увеличением массовой доли иона хлора [Сl] в материале его безопасная влажность W
σ
растет при
малых значениях насыпной плотности γ
н
и уменьшается - при больших ее значениях.
Выпишем члены формулы (5) (где
σ
= 0), содержащие [Сl] и определим С[Сl], где
С = 0,4998W - 2,708
γ
. При переборе сочетаний минимальных и максимальных значений факторов
W и t все значения С будут положительными:
W
γ
C W
γ
C
15 1,7 2,886 15 1,4 3,698
9 1,7 0,1099 9 1,4 0,702
5
С увеличением массовой доли иона хлора [Сl], как следует из формулы (5) (для t
c
при
σ
= 0),
5
температура смерзания материала уменьшается ((-t
с
) растет). Эта же зависимость видна из
графиков и находит физико-химическое объяснение.
Выпишем члены формулы (6), содержащие [Сl]; получим d[Cl], где
d = -0,12626W - 0,03843t.
При переборе сочетаний минимальных и максимальных значений W и t, одновременно
встречающихся в опытах, все значения d будут отрицательными.
W t d W t d
15 33 -0,626 15 12 -1,43
9 28 -0,06 9 12 -0,675
С увеличением массовой доли иона хлора [Сl], как вытекает из формулы (6), сопротивление
одноосному сжатию σ снижается; следовательно, эта формула также допускает приближённую
интерпретацию.
Выбор формулы для расчета сопротивления одноосному сжатию смерзшегося материала.
Сравнение формул (1) и (6) для расчета σ показывает, что чисто эмпирическая формула (6)
гораздо точнее формулы (1), которая дает погрешности, существенно превышающие ошибку
воспроизводимости опыта.
Для коррекции формулы (1) по 153 экспериментальным данным (табл. 1) пришлось
пересчитать коэффициенты σ
т
и К методом наименьших квадратов [6]. Получили σ
т
= 0,4146; К =
0,07574; СО остаточной погрешности формулы (1) с коэффициентами (7): S
oσ
= 0,83 кг/см
2
.
Качество формул (1) с (7) и (6) проверялось по признаку «смерзаемости» образца. Как видно
из табл. 1, в опытах смерзается 58 образцов (прочность до 4 кг/см
2
); согласно формулам (1) с (7) -
21, а согласно формуле (6) – 57. Ошибка определения смерзаемости образца по формулам (1) с (7),
если он смерзается на самом деле, составляет 64%, а по формуле (6) - 2%.
Не смерзались 94 образца; согласно формулам (1) с (7) - 94, а согласно формуле (6) - 71.
Ошибки определения несмерзаемости образца по формулам (1) с (7), если он смерзается на самом
деле, составляет 0%, а по формуле (6) - 24%.
Количественно формулы (1) с (7) проверим по альфа-критерию однородности СО
остаточной ошибки S
oσ
и ошибки воспроизводимости S
σн
[7]. Для формул (1) с (7) отношению
Фишера
2
н
2
/
σσ
SSF
o
= = 0,83
2
/0,44
2
= 3,56 с числами степеней свободы 151 (числителя) и 154
(знаменателя) соответствует уровень значимости
α
ˆ
< 10
-7
. Это свидетельствует о неоднородности
СО или о неадекватности формулы (1) с (7) результатам наблюдений. Для формулы (6) получаем,
что отношению Фишера
2
н
2
/
σσ
SSF
o
= = 2,18 с числами степеней свободы 53 (числителя) и 154
(знаменателя) соответствует уровень значимости [4]
α
ˆ
≈
10
-4
. Это свидетельствует об
однородности СО (или об адекватности ЭФР (6) результатам наблюдений), хотя и на очень низком
уровне ответственности за вывод [7; Т2Р1].
Итак, формула (1) с коэффициентами (7) исключается из дальнейшего анализа.
Гарантия несмерзаемости сыромолотой известняковой муки. Сформулируем задачу
количественно. По имеющимся данным необходимо найти зависимость минимального значения σ
г
гарантированного сопротивления одноосному сжатию от определяющих факторов и, в частности,
от содержания хлор-иона [Сl] в сыромолотой извести.
Решение задачи. Предельное значение величины
σ
задано:
σ
п
= 2 кг/см
2
. СО ошибки
расчета величины
σ
по формуле (6) составляет S
oσ
= 0,65 кг/см
2
. Примем доверительную
вероятность равной 95%. Считая распределение величины σ нормальным [7] и уменьшив
заданную величину
σ
п
на 2S
oσ
, получим
σ
г
= 2 – 2•0,65 = 0,7 кг/см
2
. Подставив это значение в
формулы (4) и (6) и выразив их через [Сl], найдем:
[
]
1г
ˆ
lC = 4,128γγ
н
– 0,01374Wt - 8,292 + 0,03368t; (8)
нн
г2
ˆ
(11,87010,44254,13)/(0,038430,12626)
ClWtW
γγγ
=+++
. (9)
Примем наиболее «тяжелые» условия по плотности и влажности: γ = 1,7 кг/дм
3
; γ
н
= 1,16
кг/дм
3
; W = 15 %. Подставив эти значения в формулы (8) и (9), получим:
[Сl]
г1
= - 0,1724t - 0,1516; (10)
[Сl]
г2
= 3,9738 (1,894 + 0,03843t). (11)
6
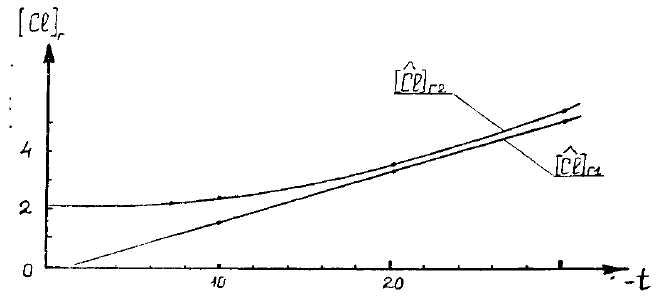
Результаты расчетов по формулам (10) и (11) хорошо совпадают (см. рисунок) при
отрицательных температурах 16 ≤ (-t) ≤ 30 °C; экстраполяция по формуле (10) более
правдоподобна, чем по (11). Кроме того, формула (10) вытекает из формулы (8), а последняя - из
формулы (4), полученной, в свою очередь, по методу наименьших квадратов, который дает
наиболее точную, несмещенную оценку значений [Сl]. Поэтому для практических расчетов
рекомендуется использовать формулу (8).
Рисунок. Зависимость от температуры t °С концентрации иона хлора [Сl]
г
, в известковой
муке, гарантирующей с вероятностью 95% несмерзаемость материала при влажности W = 15%,
плотностях: насыпной γ
н
= 1,16 кг/дм
3
, установочной γ = 1,7 кг/дм
3
и [Cl]
г1
- по (10); [Cl]
г2
- по (11).
Таким образом, экспериментальное исследование процесса смерзаемости сыромолотой
известняковой муки Ковровского карьероуправления позволило получить эмпирические формулы
(3) - (6), описывающие зависимости параметров физических свойств смеси от различных
факторов.
Для определения концентрации иона хлора в смеси, гарантирующей с вероятностью
95% несмерзаемость груза в зависимости от его физических свойств и требуемой
температуры, рекомендуется пользоваться формулой (8).
Литература
1. ТУ РСФСР-557-78. Мука известняковая из отходов. – М., 1978.
2. Мамаева А. М., Воротникова Н. Н., Дубовая В. К. Смерзание известковых и
гипсосодержащих материалов в зависимости от влажности и добавок // Химия в сельском
хозяйстве. – 1975. - №2. – С. 59 – 61.
3. Временное руководство института ПромтрансНИИпроект по определению
прочности смерзания насыпных грузов, провозимых в ж-д вагонах /
ПромтрансНИИпроект. – М., 1977. – Вып. 4232.
4. Северинова Э. М., Разин Г. М., Игнатова Н. В. Определение основного параметра
прочности смерзшихся насыпных грузов - сопротивления одноосному сжатию /
ПромтрансНИИпроект. Труды. – Вып. 9. – М.: Стройиздат, 1978. – С. 97 – 137.
5. Круг Г. К. и др. Планирование эксперимента в задачах нелинейного оценивания и
распознавания образов. – М.: Haука, 1981. - 172 с.
6. Рудай А. Н., Цейтлин Н. А., Рудaй В. И., Ицков Ф. Э. Разработка рациональных
процедур программы линейного регрессионною анализа // Статистические методы в
основной химии: Труды. Т. 63/НИОХИМ. - Харьков, 1986. – С. 72 – 84.
7. Цейтлин Н. А. Применение методов математической теории эксперимента в содовой
промышленности: Обзор. Информ. / Сер. Содовая пром-сть. – М.: НИИТЭХИМ, 1984. - 36
с.
1
9. Метрология. Оценка методами планирования многофакторного эксперимента
метрологических характеристик методик рентгенофлуоресцентного анализа в тонком слое
Реферат
Ключевые слова: рентгенофлуоресцентный анализ, градуировочная функция прибора,
планирование эксперимента, математическая статистика, факторный план, проверка
статистических гипотез, адекватность, структурная идентификация, тяжёлые элементы,
водный раствор, методика выполнения измерений, аттестация методики.
Проведены исследования, позволяющие оптимально планировать градуировочные
эксперименты для построения градуировочной функции прибора, определяющего концентрации
компонентов водного раствора методом рентгено - флуоресцентного анализа, а также аттестации
метода выполнения измерений.
Описаны особенности задачи планирования градуировочных экспериментов: возможность
независимого варьирования концентрациями компонентов; решение обратной задачи
планирования эксперимента; оценивание параметров в обратной задаче регрессионного анализа;
наличие одной существенной и ряда менее существенных переменных в моделях; необходимость
одновременной проверки ряда статистических гипотез; необходимость расширения области
определения градуировочных функций; проверка адекватности системы градуировочных
функций; структурная идентификация градуировочной функции; непостоянство дисперсии
погрешности измерения интенсивности линий спектров элементов.
Основываясь на этих особенностях задачи составлены методики оптимального
планирования градуировочного эксперимента и построения градуировочной функции прибора, а
также метрологической аттестации методики выполнения измерений.
Приведен пример построения градуировочной функции для определения концентраций
элементов Cr и Ni методом рентгено - флуоресцентного анализа.
Сформулированы задачи будущих исследований.
Благодарности
Размеры моей благодарности будут безграничны в пределах разумного. (Семён Альтов)
Автор приносит благодарность коллегам за помощь в работе: Скоробогатько Ю. В. и
Скоробогатько Л. М. – за составление программ для ПЭВМ, статистическую обработку данных и
помощь в оформлении работы; Ицкову Ф.Э. – за подготовку раздела 1.3; Антонову С. В. и
Полосухиной Л. А. – за обсуждение постановки задачи исследования; Квасову В. А. и Чкалову И.
И. – за проведение экспериментов.
Словарь терминов
Пояснительные выражения объясняют тёмные мысли. (Козьма Прутков)
ГРАДУИРОВОЧНАЯ ФУНКЦИЯ (градуировочная характеристика средства измерения) -
зависимость между значениями величины на выходе и входе средства измерения (СИ),
представленная в виде формулы.
ФАКТОР - переменная величина, по предположению, влияющая на результаты
эксперимента.
ОБЛАСТЬ ЭКСПЕРИМЕНТИРОВАНИЯ - область факторного пространства, где могут
размещаться точки, отвечающие условиям проведения опытов.
ПОСЛЕДОВАТЕЛЬНЫЙ ЭКСПЕРИМЕНТ
– эксперимент, реализуемый в виде серий, в
котором условия проведения каждой последующей серии определяются результатами
предыдущих.
ФУНКЦИЯ НАДЁЖНОСТИ
()
U
α
- вероятность
α
того, что случайная величина примет
значение, большее, чем U.
ОТКЛИК - наблюдаемая случайная переменная, по предположению зависящая от
факторов.
ФУНКЦИЯ ОТКЛИКА - зависимость математического ожидания отклика от факторов.

2
МАТРИЦА ПЛАНА - стандартная форма записи условий проведения экспериментов в виде
прямоугольной таблицы, строки которой отвечают опытам, столбцы - факторам (здесь -
концентрациям компонентов X
i
). При построении градуировочных функций используется понятие
матрица «плана» (в кавычках), в которой роль факторов играют интенсивности Y линий
спектров элементов.
РАНДОМИЗАЦИЯ ПЛАНА - прием планирования эксперимента, имеющий целью свести
эффект некоторых неслучайных факторов к случайной ошибке.
ПАРАЛЛЕЛЬНЫЕ ОПЫТЫ - рандомизированные во времени опыты, в которых уровни
всех факторов сохраняются неизменными.
РЕГРЕССИОННАЯ МОДЕЛЬ
- зависимость отклика от количественных факторов и
ошибок наблюдения отклика.
АДЕКВАТНОСТЬ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
- соответствие математической
модели экспериментальным данным по выбранному критерию.
ЭФФЕКТ ВЗАИМОДЕЙСТВИЯ ФАКТОРОВ - показатель зависимости изменения
эффекта одного фактора от уровней других факторов.
ПОЛНЫЙ ФАКТОРНЫЙ ПЛАН (ЭКСПЕРИМЕНТ) - план (эксперимент), содержащий
все возможные комбинации всех факторов на определенном числе уровней равное число раз.
ДРОБНЫЙ ФАКТОРНЫЙ ПЛАН (ЭКСПЕРИМЕНТ) - план (эксперимент), содержащий
часть комбинаций полного факторного плана (эксперимента).
Аббревиатуры
ГФ - градуировочная функция;
ДФЭ и ПФЭ – дробный и полный факторный
эксперимент;
ЛПР
– лицо, принимающее решение;
МВИ - методика выполнения измерений содержания
тяжелых элементов в пробах водных растворов;
МТЭ - математическая теория эксперимента;
ПЭВМ - персональная электронная
вычислительная машина;
РФА - рентгеноспектральный
флуоресцентный анализ;
СО - среднеквадратичное
отклонение;
ЧСС - число степеней свободы.
Перечень условных обозначений, символов и единиц
i - число натурального ряда; код наименования
элемента;
X
i
- концентрация элемента i в водном растворе,
кг/кг (кг элемента на кг раствора или мг/л);
Y
i
- интенсивность линии спектра
флуоресцентного излучения определяемого
элемента i, i/с;
i
β
,b
i
- коэффициент регрессии и его выборочная
оценка;
S,
σ
- СО случайной величины и её выборочная
оценка;
22
,Sσ - дисперсия случайной величины и её
выборочная оценка;
R
2
- коэффициент детерминации;
f - число степеней свободы (ЧСС) оценок S или
S
2
;
→ − является точечной (однозначной)
статистической оценкой параметра (например, b
i
→
i
β
: значение b
i
является точечной оценкой
параметра
i
β
); используются точечные оценки
коэффициентов b
i
→
i
β
, a
i
→
i
α
, дисперсий
n - число компонентов в растворе;
N - число опытов (точек) в плане
эксперимента;
N
0
, N
3
- число опытов в центре плана и в
звездных точках;
i
Y - среднее значение величины Y
i
;
Y - вектор N-мерный;
YX, - матрицы размерностью N × (n+1)
(первый столбец матриц X и Y состоит из
единиц);
XH
Ω
- область наблюдаемых значений X
i
концентраций элементов i в растворах;
YX
Ω
Ω
, - области экспериментирования в
пространстве факторов - концентраций (X),
или интенсивностей (Y);
δ
- математическое ожидание
(систематическая составляющая)
абсолютной погрешности результата
измерения;
δ
σ
- СО абсолютной погрешности

3
22
ii
Sσ→и СО
ii
S
σ
→
;
∆
→
∆
;
∆
S
→
∆
σ
;
результата измерения;
Н
0
, Н
1
- нулевая и альтернативная гипотезы.
При построении ГФ использовался аппарат МТЭ, включающей теорию планирования
эксперимента и математическую статистику [5-10,12-19]. Поэтому термины и обозначения, в
основном, заимствованы из этих двух дисциплин.
Однако между терминами и обозначениями в областях МТЭ и метрологии [20] существуют
некоторые различия, иногда принципиальные. Например, в МТЭ используется термин «случайная
величина» (СВ) и обозначается она символом Х (или У), а в метрологии – «погрешность
результата измерения» и обозначается
∆
Х
ИЗМ
; в МТЭ: СО СВ - S
X
, в метрологии: «средняя
квадратическая погрешность (СКП) единичного измерения» - S; в МТЭ: СО среднего
арифметического -
−
X
S и СО оценки ГФ; в метрологии: СКП результата измерений -
−
X
S .
Ряд терминов разъясняется в тексте по мере их употребления.
Введение
Чем больше в книге воды, тем она глубже. (Андрей Кныше)
Группа специалистов УКРНЦОВ (Украинского научного центра охраны вод в г. Харькове)
Полосухина Л. А., Антонов С. В.
и др.
разработала методики концентрирования и
рентгенофлуоресцентного определения состава сточных вод [1]. Аппаратурно эти методики
обеспечены рентгенофлуоресцентными анализаторами (см. приложение). Разработанные
методики позволяют одновременно определять содержание ряда элементов в пробе в заданном
диапазоне концентраций. Для построения ГФ средства измерения с использованием
разработанных методик традиционными методами [2] было бы необходимо провести очень
большое количество экспериментов. В начале 1990-го года Л. А. Полосухина обратилась к автору
с просьбой адаптировать современные методы математической теории эксперимента для
существенного сокращения числа опытов без потери точности ГФ. Задача оказалась не
простой; на её решение ушёл почти год.
При решении задачи планирования эксперимента был учтен ряд особенностей объекта
исследования; проанализированы существующие методы решения подобных задач; были
использованы методы планирования эксперимента и обработки данных, ориентированные на
решение прямых и обратных задач регрессионного анализа [З-7].
Обычно в работах, подобных настоящей, авторы полностью приводят алгоритмы
планирования эксперимента и обработки результатов наблюдений. Такое изложение возможно
ввиду сравнительной простоты решаемых задач. Сформулированная в настоящей работе задача
представляется довольно сложной в силу описанных ниже особенностей. Для её корректного
решения приходится привлекать большое количество современных методов планирования
эксперимента и обработки результатов наблюдений, многие из которых обеспечены
стандартными программами для ПЭВМ [7]. В силу сказанного, не представляется возможным
изложение в настоящем разделе исчерпывающего описания алгоритма планирования
градуировочного эксперимента и обработки данных. Здесь излагаются и обсуждаются только
основные принципы, лежащие в основе методов построения ГФ и метрологической аттестации
МВИ. Приводятся литературные источники, в которых подробно излагаются используемые
алгоритмы и программы для ПЭВМ. Изложенные методики иллюстрируются примерами.
9.1. Особенности задачи построения градуировочных функций
Ключевой вопрос математики: не все ли равно? ( В. Шендерович).
Для анализа содержания тяжелых элементов в растворах предложено использовать [1]
метод рентгеноспектрального флуоресцентного анализа (РФА; см. Приложение).
Суть метода заключается в том, что при рентгеновском облучении специальным образом
подготовленных образцов каждому набору элементов тяжелых металлов с концентрациями X
i
),1( ni =
в водном растворе соответствует определенная интенсивность Y
i
),1( ni=
ана-
4
литических линий элемента, такая, что
),...,,(
21 nii
XXXYY
=
, ni ,1= , (1.1)
где n - число компонентов в водном растворе (кроме самой воды).
Для нас представляет интерес случай, когда справедливым является также и обратное
соотношение [2, с. 117]: каждому набору интенсивностей Y
i
аналитических линий элементов
отвечает определенная концентрация элемента X
i
, то есть
),...,,(
21 nii
YYYXX
=
, ni ,1= (1.2)
Возникает задача построения градуировочных функций, необходимых для определения
концентраций X
i
компонентов i в многокомпонентном водном растворе методом РФА.
При планировании градуировочного эксперимента и обработке его результатов для
решения этой задачи следует учитывать ряд особенностей.
9.1.1. Необходимость расширения области определения градуировочных функций.
Выбор области
x
Ω
определения градуировочных функций прибора обусловлен рядом
факторов. Допустим, прибор предназначен для контроля содержания определенного набора из
n тяжелых элементов в сбросных водах промышленного предприятия. Статистические данные,
собранные за длительный срок работы предприятия, как правило, свидетельствуют о высокой
положительной корреляции концентраций X
i
элементов (значения коэффициентов корреляции
лежат в пределах от 0,8 до 0,999). Нижние
−
i
X
и верхние
+
i
X
пределы значений концентраций
различных компонентов могут существенно различаться.
Окаймим область
xн
Ω
наблюдаемых значений концентраций какой-нибудь фигурой,
например, эллипсом (при n = 2; при n > 2 эллипс будет многомерный). Возможно проведение
градуировочного эксперимента в пределах области
xн
Ω
путем приготовления эталонных
растворов с приблизительно пропорциональным возрастанием значений концентраций всех
компонентов. Однако такой план приведет к почти вырожденным матрицам X и Y , что
сделает проблематичной раздельную оценку коэффициентов градуировочных функций [9]. Для
независимой оценки коэффициентов градуировочных функций матрица Y "плана"
эксперимента должна быть близка к ортогональной. Это требование приводит к
существенному расширению области эксперимента за счет включения точек, лежащих вне
пределов упомянутого эллипса. Область эксперимента становится параллелепипедом (при n =
3; при n > 3 параллелепипед многомерный), где ),(
+−
∈
iii
XXX .
Другим требованием, приводящим к еще большему расширению области эксперимента,
является необходимость определения существенно изменяющихся соотношений X
i
/X
j
между
различными компонентами данной группы. Удовлетворить этому требованию можно путем
уменьшения нижних значений
−
i
X всех компонентов до нуля. Таким образом, область
x
Ω
определения градуировочных функций может быть определена как параллелепипед
{
}
niXXX
iiix
,1),,0(: =∈=Ω
+
.
При необходимости измерения концентрации X
i
компонента i в растворе, принимающей
значения
+
>
ii
XX , выходящие за пределы области
x
Ω
эксперимента, или, наоборот, очень
малых, близких к нулю значений, можно соответственно разбавлять пробу раствора для
анализа, или наоборот, использовать большие объемы для концентрирования пробы раствора
на образце.
9.1.2. Возможность независимого варьирования концентрациями компонентов.
Поскольку обычно метод РФА используется для определения концентраций X
i
всех n+1
компонентов, составляющих смесь, включая и концентрацию воды X
n+1
, то для построения
градуировочной функции используются планы на симплексе [3, 4]. Существенным в этих
планах является естественное ограничение

5
1
1
=
+
+n
XZ, где
∑
=
=
n
i
i
XZ
1
(1.3)
В нашу задачу входит определение концентраций только n компонентов системы
(исключая воду). Ограничению (1.3) можно удовлетворить, варьируя концентрацию воды X
n+1
.
Таким образом, переменные X
1
, X
2
, …, X
n
можно считать независимыми факторами, которые
могут принимать любые заданные значения в пределах естественного ограничения Z < 1 . Для
сточных вод гальванических цехов характерно, что Z << 1. В общем случае для водных
растворов Z < 1; при Z = 1 смесь не является водным раствором (X
n+1
= 0).
Возможность независимого варьирования переменными X
1
, X
2
, …, X
n
позволяет
воспользоваться методологией планирования факторного эксперимента [5].
Уместно отметить наличие скрытого фактора в ГФ - объема V пробы раствора,
подлежащего выпариванию на подложке. Согласно инструкции [1] объем V в опытах
сохраняется постоянным. Объем V пробы раствора определяет массы m
i
элементов,
концентрируемых на подложке. Значения масс m
i
определяют распределение интенсивностей
Y
i
линий спектра элементов i. Таким образом, определяющими факторами в задаче являются не
концентрации X
i
элементов, а их массы m
i
на подложке. Однако поскольку между величинами
m
i
и X
i
существуют взаимно однозначные соответствия, а конечной целью МВИ является
определение концентраций X
i
элементов, а не их масс m
i
на подложке, то в качестве факторов
в задаче построения ГФ будем использовать концентрации X
i
элементов в пробах. Данный
подход имеет ещё и то преимущество, что при неизвестных концентрациях различных
компонентов раствора не требуется изменения объема пробы для определения концентраций.
9.1.3. Обратная задача планирования эксперимента.
В теории планирования экспериментов обычно решается прямая задача: установить
такие значения факторов X
i
в опытах, которые обеспечили бы получение лучшей, например, по
точности, зависимости отклика Y от факторов. Прямая задача теории планирования
экспериментов может быть непосредственно использована при построении зависимостей (1.1).
Авторы известных нам работ [3, 4] так и поступают. Строят модель вида (1.1) [2, с. 119], а
затем рекомендуют пользователям определять нужные для практики значения концентраций X
i
по известным значениям интенсивностей Y
i
путем решения системы из n уравнений (1.1) с n
неизвестными X
i
[2, c. 115].
При использовании факторных планов подобный путь получения формул (1.1) позволяет
легко выполнять расчеты коэффициентов и их уровней значимости даже без использования
ПЭВМ [5]. Однако он имеет два недостатка:
1) необходимость использования вычислительной техники для решения системы
уравнений (1.1);
2) существенным является тот факт, что при расчете коэффициентов уравнения (1.1)
используется метод наименьших квадратов, направленный на уменьшение дисперсии ошибки
расчета откликов Y
i
. В то же время, решение системы уравнений (1.1) приводит к определению
значения факторов X
i
, дисперсии ошибок расчета которых не минимальны!
Преодоление этих недостатков возможно следующим путем.
Учтем, что зависимости (1.1) и (1.2) описывают взаимно однозначное соответствие
между векторами концентраций
X
и интенсивностей
Y
. Для практики предполагается
целесообразным использовать две аппроксимации указанного взаимно однозначного
соответствия с помощью эмпирических формул, явно выраженных относительно
определяемых переменных. Для интенсивностей линий (1.1) используем модели регрессии
0...
111
......;1,
n
iiiiijijijkijkinijnуi
iijnijkn
YXXXXXXXXXEin
βββββ
=≤≤≤≤≤≤≤
=++++++=
∑∑∑
(1.4)
где Е
уi
- случайные ошибки откликов.
Для концентраций компонентов используем градуировочные функции
0...
111
......;1,
n
iiiiijijijkijkijnijn хi
iijnijkn
XYYYYYYYYYEin
ααααα
=≤≤≤≤≤≤≤
=++++++=
∑∑∑
. (1.5)
Конечной целью планирования градуировочного эксперимента является
построение градуировочных функций (1.5), в которых роли факторов и откликов меняются

6
местами!
План эксперимента, основанный на установлении определенных значений факторов X
i,
легко сделать оптимальным только для модели (1.4) [3, стр. 184].
После проведения градуировочного эксперимента получаются две матрицы одинаковой
размерности: матрица плана X - матрица заданных концентраций X
i
элементов и матрица
откликов Y - матрица интенсивности аналитических линий. Матрица Y служит "планом" (в
кавычках) для расчета коэффициентов
i
α
формулы (1.5). Такой "план" не будет оптимальным
для построения модели (1.5). В качестве примера покажем, что ортогональный план
эксперимента для переменных X
i
даже в случае линейных по регрессорам моделей (1.4) и (1.5)
не ведет к ортогональности матрицы переменных Y
i
, полученной в результате
соответствующих экспериментов.
Обозначим
j
Y
ˆ
- N-мерный вектор оценок зависимой переменной
j
Y , имеющей
случайную составляющую, X - ортогональная матрица плана независимых переменных. Тогда
[5]
jj
YXXXXbXY
~
ˆ
1
′
′
==
−
, (1.6)
где b - вектор оценок коэффициентов регрессии,
j
Y
~
- опытные значения переменной
j
Y .
Так как X - ортогональная матрица, то матрица
(
)
1−
′
= XXD также ортогональная:
()
n
XXD
λ
λ
0
...
0
1
1
=
′
=
−
. (1.7)
Для того, чтобы в результате экспериментов по плану X образовалась ортогональная
матрица плана G по переменным
j
Y , необходимо и достаточно, чтобы G
`
G была
диагональной. Выполним соответствующие преобразования
(
)
(
)
nn
YXDXYXDXYYYG
~
,...,
~
ˆ
,...,
ˆ
,
ˆ
121
′′
== . (1.8)
Легко показать, что
XXXDX
n
i
i
′
=
′
∑
=1
λ , (1.9)
а значит
(
)
(
)
(
)
(
)
11
11
,...,,...,
nn
nn
ii
ii
GXXYXXYXXYY
λλ
==
′′′
==
∑∑
%%%%
, (1.10)
′
′
′
′
′
′
′
′
′
′
′
′
=
′
∑
=
nnn
n
n
n
i
i
YXXYYXXY
YXXYYXXY
YXXYYXXY
GG
~~
...
~~
.........
~~
...
~~
~
~
...
~
~
1
212
111
2
1
λ . (1.11)
Каждый элемент построенной матрицы можно представить в виде
(
)
(
)
jiji
YXYXYXXY
~
~
~
~
′′
=
′
. (1.12)
Заметим, что
(
)
(
)
(
)
′
=
′
inii
YXYXYX
~
,,...,
~
,
~
1
(1.13)
где
j
X - вектор-столбец значений переменной X
j
.
Для того, чтобы матрица G`G была диагональная, необходимо, чтобы столбцы матрицы
