Цейтлин Н.А. Из опыта аналитического статистика

Подождите немного. Документ загружается.

9.3.3. Подготовка исходных данных.

Для метрологической аттестации МВИ готовят N эталонных растворов с концентрациями

элементов в каждом X

( Njni ,1;,1 == ). Далее с помощью МВИ выполняют по m измерений

концентраций элементов X

ijk

( mk ,1= ). Вычисляют значения абсолютных погрешностей

∆

ijk

= X

ijk

– X

, (3.1)

оценки систематических составляющих

абсолютной погрешности

ijk

∆=∆

∑

δ→∆

; (3.2)

оценки S

∆

СО

случайных составляющих абсолютных погрешностей

()

0.5

ijijk

∆



=∆−∆−





∑

, S

∆

→

(3.3)

с f = m - 1 степенями свободы каждая.

Осуществляется очистка данных от выбросов (грубых ошибок) путем винсоризации [6]

(исправления) выскакивающих значений погрешностей

∆

ijk

. Выскакивающие значения

определяются по критерию Смирнова-Груббса [6]. Вычисляются статистики критерия

()

ijk

∆

∈

∆−∆= /max

ξ (3.4)

Если находится такое k = q, что значение

превышает критическое

j(m-1)

уровня

c m - 1

степенями свободы, то соответствующее значение

∆

ijq

абсолютной погрешности заменяется на

ближайшее к нему не выскакивающее значение [Р2.3].

При проверке статистических гипотез будем использовать критерии, основанные на

предположении о нормальном законе распределения погрешностей результатов измерений.

Отметим, что проверка согласия наблюдаемых распределений с нормальным [Р2.5]

выливается в очередную довольно сложную задачу: требуется проверить согласие распределения

N случайных величин на основе выборок объемом m элементов каждая. Все критерии согласия

становятся достаточно мощными при больших выборках (m > 25) [12], а это удорожает

исследования. Разумеется, при достаточных времени, средствах и наличии ПО ПЭВМ по

статистике процедура проверки согласия распределений не вызывает затруднений.

9.3.4. Постановка задачи метрологической аттестации методики выполнения измерений

МВИ содержания химических элементов в растворе [1] включает описание

последовательности действий, завершающихся результатами измерения концентраций X

ni ,1= элементов в растворе с указанием значений S

→

СО суммарной погрешности

измерений.

Задачи метрологической аттестации МВИ

следующие.

А) Проверка соответствия случайных составляющих погрешностей результатов измерений

паспортным характеристикам, выражающегося в гипотезах

Xiii

H σσ

, ni ,1= против

Xiii

H σσ

≠:

(3.5)

где

- двусторонние альтернативные гипотезы.

Б) Проверка содержательных гипотез о правильности результатов измерений,

сформулированных в виде нулевых статистических гипотез

0ij

H о равенстве нулю

систематических составляющих погрешностей результатов измерений,

ijij

H δ

, niNj ,1;,1 == против

≠

iiij

H δ

, (3.6)

где

- двусторонние альтернативные гипотезы о неправильности результатов измерений.

Если нулевые гипотезы (3.5) и (3.6) не отклоняются, метрологическая аттестация МВИ

завершается. Если некоторые из гипотез

H (3.6) отклоняются, необходимо решать следующую

задачу.

В). Коррекция ГФ МВИ. Значения концентраций

X и интенсивностей

Y , полученные в

результате градуировочного эксперимента, объединяют с результатами

X ,

Y метрологической

аттестации (присваивая последним результатам в случае необходимости большие значения

весовых коэффициентов) и обрабатывают методами регрессионного анализа.

Если некоторые из гипотез

H (3.5) отклоняются, то в паспорт МВИ записываются

соответственно новые значения СО погрешностей измерения.

9.3.5. Решение задачи метрологической аттестации МВИ содержания элементов в растворе.

До начала экспериментов по метрологической аттестации ЛПР необходимо задать уровень

значимости

[Т2Р1] для проверки гипотез. Пусть, например, уровень ответственности за вывод

будет большой. Если ЛПР намерено выявить ошибочность паспортных характеристик МВИ,

предпочтительной является альтернативная гипотеза и критический уровень значимости задается

малый, например,

= 0,01; если ЛПР намерено подтвердить правильность паспортных

характеристик МВИ, предпочтительной является нулевая гипотеза и критический уровень

значимости задается большой например,

= 0,2 . Если уровень ответственности за выводы

обычный, то в обоих случаях можно принять

= 0,05.

Задача проверки гипотез

делится на n, вообще говоря, отдельных задач проверки

гипотез для каждого элемента i в отдельности (

ni ,1=

). В свою очередь, начинать проверку

каждой из n гипотез необходимо с проверки однородности СО S

∆ij

во всех N измерениях, то есть

гипотез

ikiji

δδ

σσ =:

{

}

ni ,1∈ ; 1 < j < k < N; против

ikiji

δδ

σσ ≠:

. (3.7)

Для проверки гипотез

H (3.7) используется критерий Фишера-Бонферрони, изложенный

выше в [Р1]. Полученные по формулам (1.29) и (1.30) значения оценок уровней значимости

сравниваются с критическими

. Если

, соответствующие гипотезы

H (3.7) не

отклоняются. Это позволяет получить средние значения однородных СО по формуле (1.25) с

Nff =

степенями свободы.

СО

∆

являются оценками СО

δi

случайных составляющих погрешностей элементов.

Для проверки n гипотез

(3.5) вычисляются n статистик критерия Фишера [10]

{

}

{

}

{

}

iзiчii

SSSSffF ,min/,max2/

∆∆

=α

, (3.8)

где f

чi

и f

зi

- числа степеней свободы числителя и знаменателя F-отношения; ff

чi

= и

Xзi

, если

SS >

∆

или

Xчi

и ff

зi

= , если

SS <

∆

. Затем с помощью

функции распределения Фишера [10, 12, 15] при известных f

чi

, f

зi

определяется

′

(равное

), вычисляется аргумент

′

αα 2

; принимается l = n и по формуле (1.22) определяется

значение

Если

все n гипотез

не отклоняются. В этом случае рекомендуется в паспорте

прибора привести уточненные значения СО случайных погрешностей

(

)

(

)

[

]

5.0

XXiXiXi

ffSfSfS ++=

′

ni ,1=

, (3.9)

имеющие

fff +=

′

ЧСС.

При отклонении гипотез

H (3.7) приступают к сведению неоднородных СО S

∆ij

отдельные однородные группы [10]; при отклонении гипотез

(3.5) в паспорт МВИ

вписывают вновь обнаруженные значения СО случайных погрешностей S

∆i

Для проверки гипотез

(3.6) используется критерий Стьюдента-Бонферрони

(предложенный Фишером [17, с. 128], [10]). Вычисляются n статистик критерия

{

}

ijij

Smlft

∆













∆= /max/

α , (3.10)

где переменные f , i, j,

∆ , m,

∆

определены выше. По таблицам распределения Стьюдента

[12], или по номограмме этого распределения [18], или по аппроксимирующим формулам [10] при

известных значениях чисел степеней свободы f и статистиках

(3.10) определяются аргументы

(равные

min ) формулы (1.22); аргумент l = 2nN (т. к. альтернативные гипотезы -

двусторонние). Тогда

tij

min2

или

(

)

tij

min11

αα −−= при

3.0

. (3.11)

Если

все нулевые гипотезы Н

0ij

не отклоняются (все измерения считаются

правильными); если

выделяются измерения, имеющие значимые систематические

составляющие погрешности и приступают к коррекции соответствующих ГФ.

9.4. Примеры построения градуировочных функций для определения концентраций элементов

методом рентгенофлуоресцентного анализа

Доказанное примерами никогда нельзя считать полностью доказанным. (Г. Лейбниц)

4.1. Пример 1. Два элемента - Cr и Ni.

При построении ГФ ориентировались на операторную схему, приведенную в п.2.

А. Объектом исследования являются сточные воды гальванического цеха. Уровень

ответственности за выводы приняли большой. Пользуясь [Т2Р1] задали критические значения

уровня значимости, если предпочтительна нулевая гипотеза (для проверки адекватности моделей)

= 0.1, если альтернативная (для проверки значимости коэффициентов ГФ) -

= 0.03.

В сточных водах имеются ионы хрома Cr

и никеля Ni

. Для удобства закодировали

названия определяемых элементов номерами: i = 1 - для Cr, i = 2 - для Ni. Пределы наблюдаемых

изменений концентраций этих элементов X

- от 0 до 0.5 мкг/мл.

Область планирования эксперимента - квадрат:

(

)

{

}

2,1,/5.0;0:

∈

Ω

iмлмкгXX

iiX

Б. Предварительные опыты показали, что ГФ могут быть аппроксимированы полиномами

второго порядка. Поэтому для проведения опытов воспользовались некомпозиционным планом

второго порядка 3

[24, т. 1, с. 50], включающем 9 опытов (табл. 4.1).

Каждую точку плана дублировали по три раза.

Таблица 4.1.

План и результаты градуировочного эксперимента.

Интенсивность линий спектра элемента, с

-1

Концентрация в

пробе, мг/мл

Хром Никель

Cr, X

Ni, X

11j

12j

13j

21j

22j

23j

1 0 0 710 720 700 820 820 840

2 0,4 0 1200 1215 1250 830 840 840

3 0 0,4 700 710 710 1450 1480 (1540)* 1480

4 0,4 0,4 1170 1210 1190 1510 1490 1490

5 0 0,2 700 750 750 1240 1240 1270

6 0,4 0,2 1200 1230 1250 1160 1170 (1230)* 1170

7 0,5 0 1003 980 970 800 820 820

8 0,2 0,4 1035 1010 960 1480 1490 1470

9 0,2 0,2 970 1010 1020 1210 1210 1210

* Значения величин в скобках признаны выбросами и винсоризованы (заменены ближайшими значениями в

группах данных).

В. Для концентрирования раствора использовали пробы объемом по 0.5 мл каждая с таким

расчетом, чтобы в сухом остатке получить достаточно большие массы определяемых элементов.

Измерения выполнялись на РФА БАРС-З; время счета импульсов составляло 16 с.

Согласно плану (табл. 4.1) было приготовлено 27 растворов объемом по 5 мл; из каждого

раствора взята одна проба объемом по 0.5 мл каждая и сконцентрирована на 27-ми таблетках

путем упарки в печи в течение 1 - 2 мин. Для 54 измерений на приборе таблетки отбирались в

случайном порядке.

Г. Первичная обработка данных.

По формуле (1.26) вычисляли размахи (табл. 4.2).

Таблица 4.2

План и результаты первичной обработки данных из табл. 4.1

Концентрация

элементов в

пробе, мг/мл.

Средние значения

интенсивностей

линий, с

-1

Средние квадратич-

ные отклонения

ошибок, с

-1

Размах данных в

группах, с

-1

Cr Ni Cr Ni Cr Ni Cr Ni

j→

N↓

1 0 0 710 827 10 12 20 20

2 0.4 0 1222 837 26 6 50 10

3 0 0.4 707 1470 6 17 10 (90)

4 0.4 0.4 1190 1497 20 11 40 20

5 0 0.2 733 1250 29 17 50 30

6 0.4 0.2 1227 1167 25 6 50 (70)

7 0.2 0 984 833 17 12 23 20

8 0.2 0.4 1002 1480 38 10 75 20

9 0.2 0.2 1000 1210 26 (0.3) 6 50 0

Средние 975 1175 24 12

* См. сноску в табл. 4.1.

Наибольший размах 75 с

-1

для Cr в опыте 8 признан не слишком большим по сравнению с

остальными размахами для Cr, а размахи 90 и 70 с

-1

в опытах 3 и 6 для Ni признаны слишком

большими по сравнению с остальными размахами для Ni. Соответствующие грубые ошибки (табл.

4.1, в скобках) винсоризированы.

Вычислены средние значения интенсивностей линий спектра элементов по формуле (1.23)

(табл. 4.2).

Для выявления путаницы номеров строк были сгруппированы средние значения

интенсивностей из табл. 4.2 в три группы, соответствующие трем одинаковым концентрациям X

элементов (табл. 4.3).

Таблица 4.3

Группы интенсивностей линий спектра элементов по одинаковым концентрациям из табл. 4.2.

Концентрация в

пробе, мг/мл.

Сгруппированные средние значения

интенсивностей, с

-1

Размахи данных в

группах с

-1

Cr Ni Cr Ni Cr Ni

1 0 0 710, 707, 733 827, 837, 833 26 10

2 0,2 0,2 984, 1002, 1000 1470, 1167, 1210 18 83

3 0,4 0,4 1222, 1190, 1227 1470, 1497, 1480 37 27

Большой размах Q

= 83 с

-1

для Ni в группе 2 с концентрацией Х

= 0.2 вызван

выскакивающим значением

1167

-1

в опыте j = 6 (табл. 4.2).

Обсуждалось предположение, что в опыте 6 значение Y

236

= 1230, признанное выбросом

(табл. 4.1), на самом деле правильное, т. к. близко к средним значениям 1250 и 1210 в группе 2 для

Ni (табл. 4.3), а два других результата измерения 1160 и 1170 (оп. 6 в табл.4.1) являются грубыми

ошибками. Однако эксперты предположили, что на интенсивность линий никеля влияет высокая

концентрация хрома в растворе. Решено, что путаницы строк нет.

Вычислили СО ошибок воспроизводимости по формуле (1.24) (см. табл. 4.3). Значение СО

0.3 для Ni в опыте 9 принято в соответствии с замечанием к формуле (1.24).

В таблице 4.1 использован план типа (б) с одинаковым числом m = 3 опытов во всех точках

плана. Поэтому использовали гипотезу об однородности СО (1.27) и проверяли ее по критерию

Фишера - Бонферрони. По формуле (1.28) и табл. 4.2 для Cr нашли

{

}

40638

;2;2

F α

; для Ni -

{

}

32113.017

;2;2

F α

. По формуле (1.30) для Cr:

(

)

024.0140

=+=

−

α ; для Ni:

(

)

1011.313211

−

∗=+=

. По формуле (1.31) для Cr:

7.1024.089

∗

Поскольку 1.7 > 0.3, расчет можно (хотя и не обязательно) повторить по точной формуле

(1.31):

(

)

83.0024.011

=−−=

∗

. Поскольку 1.0

, гипотеза (1.27) не отклоняется.

Можно вычислять по формуле (1.25) S

восY1

= (5087 / 9)

0.5

= 24 c

-1

; ЧСС f

восY1

= 9

∗

2 = 18. По

формуле (1.31) для Ni:

022.01011.389

=∗∗∗=

−

Поскольку 1.0

, гипотеза (1.27) отклоняется. Очевидно, что выбросом является

минимальное значение СО S

= 0.3 c

-1

. После его винсоризации (замены на 6 с

-1

) повторим

расчеты для Ni. По (1.28): 86/17

==F ; по (1.30):

(

)

11.018

=+=

−

α ; по точной

формуле (1.31):

(

)

9998.011.011

=−−=

∗

Поскольку 1.0

, вычислим по (1.25) S

восY2

= (1195/9)

0.5

= 12 c

-1

; ЧСС f

восY2

=18.

Д. Данные столбцов X

Y табл. 4.2 обрабатывают методом регрессионного анализа [6].

Исходными структурами ГФ являются модели (1.4) и (1.5) второго порядка.

Получены следующие ГФ:

для Cr:

21237.01015676.4

−∗=

−

; S

0X1

= 0.021 мг/мл; (4.1)

для Ni:

18302.01063965.2

−∗=

−

; S

0X2

= 0.026 мг/мл. (4.2)

Коэффициенты полученных формул высоко значимы: 03.010

=<<

−

αα

Качество полученных ГФ иллюстрируется в таблице 4.4 .

Таблица 4.4

Проверка качества градуировочных функций.

Значения Ошибки

опытные расчетные натуральные стандартные

Номер

опыта

ГФ (4.1) для иона хрома

1 0,0 -0,003 0,003 0,226

2 0,4 0,408 -0,008 -0,667

3 0,0 -0,005 0,005 0,367

4 0,4 0,367 0,024 1,896

5 0,0 0,011 -0,011 -0,876

6 0,4 0,413 -0,13 -1,074

7 0,2 0,190 0,010 0,790

8 0,2 0,205 -0,005 -0,397

9 0,2 0,203 -0,004 -0,264

ГФ (4.2) для иона никеля

1 0,0 -0,002 0,002 0,160

2 0,0 0,002 -0,002 -0,123

3 0,4 0,387 0,013 0,810

4 0,4 0,409 -0,009 -0,548

5 0,2 0,229 -0,029 -1,890

6 0,2 0,176 0,024 1,511

7 0,0 0,000 -0,000 -0,009

8 0,4 0,395 0,005 0,310

9 0,2 0,203 -0,003 -0,222

Для содержательного и статистического анализов результатов наблюдений приведем также

прямые зависимости интенсивностей линий спектров элементов Y

от их концентраций X

растворах

для Cr:

111

7171545762

YXX

=+−; S

0Y1

= 26 с

-1

; (4.3)

для Ni:

222

83221421292

YXX

=+−; S

0Y2

= 26 с

-1

; (4.4)

ЧСС для СО S

формул (4.1) - (4.4) равны f

= N - q = 9 - 2 = 7, т. к. в этих формулах - по q =

2 коэффициента.

Е. Проверка адекватности формул.

Поскольку использовали план второго порядка, проверяли гипотезу (1.41). Для Cr

вычислили по (1.42) S

восХ1

= 2

∗

4.15676

∗

-7

∗

975

∗

24 = 0.019 мг/мл; для Ni аналогично S

восX2

= 2

∗

2.63965

∗

-7

∗

1175

∗

12 = 0.0074 мг/мл. По (1.20) для Cr

{

}

2.1019.0/021.0

;18;7

==αF .

Для расчета уровня значимости

воспользовались аппроксимацией [10, с.12] функции

надежности распределения Фишера:

(

)

[

]

5.0

6118.015.05.0

ZEXP ∗−−−=α (4.5)

()

[

]

(

)

aFbqFbZ ++−−=

312

;

a = 2/(9f

); b = 2/(9f

); f

, f

, 10 > F > 1. (4.6)

В примере f

= 7; f

= 18

≥

4 , поэтому а = 2/(9

∗

7) = 0.0317; b = 2/(9

∗

18) = 0.0123;

= [(1-0.0123)1.2

1/3

-1+0.0317]

/(0.0123

∗

1.2

2/3

+0.0317) = 0.145;

= 0.5-0.5[1-EXP(-0.6118

∗

0.145)]

0.5

= 0.21 >

= 0.1. Следовательно, ГФ (4.1) адекватна

ошибке воспроизводимости опыта.

Аналогично для Ni:

= 0.026

/ 0.0074

= 12.3;

{

}

1.010;18;7

=<≈

−

F αα

;

ГФ (4.2) по статистическому критерию не адекватна ошибке наблюдений. Согласно схеме в

п. 2 следует перейти к п. Ж - планированию дополнительных экспериментов. Однако эксперты

предположили, что причинами неадекватности являются неисправленные грубые ошибки

измерений в опыте 6, упомянутые выше. Кроме того, они отметили, что СО остаточных ошибок

ГФ (4.1) и (4.2) «достаточно малы и приблизительно одинаковы, что приемлемо для практики».

Далее проверяли адекватность моделей (4.3) и (4.4). По (1.39): 17.124/26

==F ;

1.0

3.0

; 7.412/26

==F ; 1.0004.0

Модель (4.3) -адекватна, а (4.4) - нет.

И. Гипотеза о близости матрицы "плана" Y к ортогональной проверялась путем проверки

гипотезы о значимости максимального недиагонального элемента корреляционной матрицы этого

плана [6]. Расчетное значение уровня значимости

= 0.99 >

= 0.1. План Y близок к

ортогональному.

Л. По формулам (1.18) - (1.20) построены интервальные оценки ГФ, которые удобнее всего

представить в графической форме (рис. 4.1, 4.2).

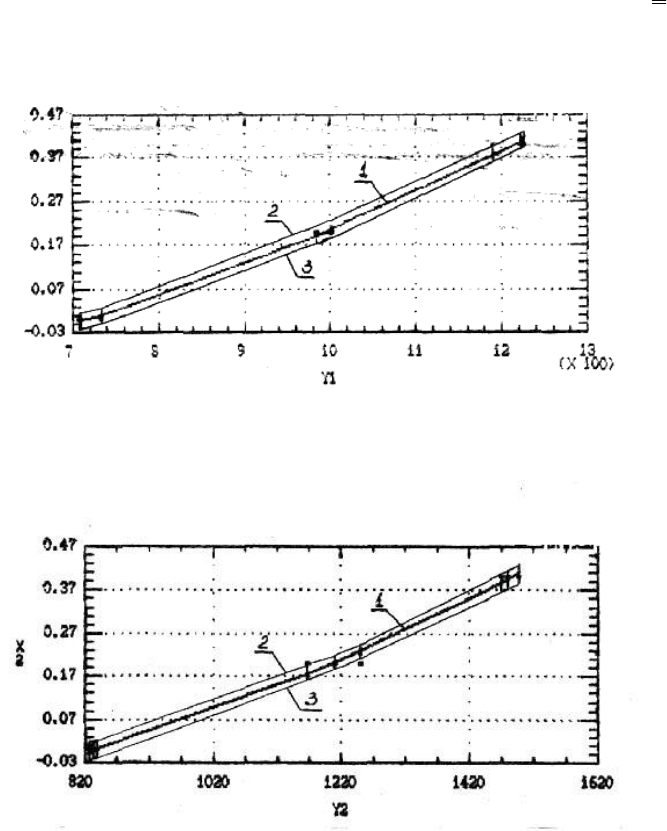
Рис. 4.1. Градуировочный график для Cr:

Точки - экспериментальные данные; Y

- интенсивность линий спектра хрома, с

-1

- концентрация

хрома в растворе, мг/мл; кривая 1 - ГФ (4.1); кривые 2, 3 - верхняя и нижняя границы 95%-ного

доверительного интервала.

Рис. 4.2. Градуировочный график для Ni:

Точки - экспериментальные данные; Y

- интенсивность линий спектра никеля, с

-1

;

- концентрация никеля в растворе, мг/мл; кривая 1 - ГФ (4.2); кривые 2, 3 - верхняя и нижняя

границы 95%-ного доверительного интервала.

Воспользуемся данным примером, чтобы проиллюстрировать процедуру обработки

результатов наблюдений, полученных с использованием плана первого порядка. Для этого

предположим, что априори не было известно о нелинейности ГФ. Тогда, согласно п. Б схемы,

строится план первого порядка – см. опыты 1 - 4 в табл. 4.1 и 4.2, соответствующие ПФЭ 2

опыт 9 в центре плана. Будем анализировать результаты 30-ти измерений на 15-ти таблетках.

Г. По (1.25): S

восY1

= 19 c

-1

; S

восY2

= 11 c

-1

; f

восYi

= 2

∗

5 = 10.

Остальные статистические характеристики приведены выше.

Д. Методом регрессионного анализа получены линейные ГФ:

для Cr: X

= 0.000802 Y

- 0.5б8; S

0X1

= 0.013 мг/мл; (4.7)

= 1244Х

+ 709; S

0Y1

= 16 с

-1

; (4.8)

для Ni: Х

= 0.000613 Y

- 0.510; S

0X2

= 0.0088 мг/мл; (4.9)

=1629Х

+ 832; S

0Y2

= 14 с

-1

. (4.10)

Коэффициенты полученных формул значимы, так как имеют уровни значимости не выше

0.002 <

к1

= 0.03 .

Е.

Для проверки гипотез (1.38) вычислим по (1.42): S

восX1

= 0.0008

∗

19 = 0.015;

восX2

= 0.0006

∗

11 = 0.0066; по (1.39):

{

}

75.0015.0/013.0

;10;3

F α ;

71.019/16

F ; 8.10066.0/0088.0

F ; 6.111/14

F .

По (4.5) и (4.6): 6.0

α ; 6.0

α ; 2.0

α ; 25.0

α . По формулам (4.7) -

(4.10) вычислим значение откликов в центре плана (см. опыт 9, табл. 4.1): 234.0

=X ;

958

=Y ; 232.0

=X ; 1158

=Y . По (1.40):

(

)

1.3]4/13/1015.0/[234.02.0

5.0

=+∗−=

t ;

(

)

0.374.019/9581000

=∗−=

t ;

(

)

5.674.00066.0/232.02.0

=∗−=

;

(

)

4.674.011/11581210

=∗−=

Для расчета уровня значимости

воспользуемся аппроксимацией функции надежности

распределения Стьюдента по формулам (4.5) и формулам [10, с. 12]

Z = L – [ L

– 2t ( f + 3)]

0.5

; L = f + 1.5t + 3 . (4.11)

В примере f = 10; L

= 10 + 1.5

∗

3.1 + 3 = 17.65 ; Z = 17.65 - [ 17.65

- 2

∗

3.1

∗

( 10 + 3 ) ]

0.5

2.454. По (4.9)

α = 0.0063. Аналогично нашли

α = 0.0065;

X 2

α = 3.4

∗

10;

Y 2

α = 3.6

∗

10.

По (1.22) :

= 1 - ( 1 - min { 0.6; 0.0063} )

= 0.019 <

= 0.1. Аналогично

= 0.013 <

;

= 10 <

;

= 10 <

. Следовательно, все линейные модели (4.7) - (4.10) не адекватны.

Согласно п. Ж следует достраивать план до плана второго порядка, затем, согласно п. В

выполняются дополнительные эксперименты и обработка данных проводится так, как описано в

начале примера.

9.4.2. Пример 2. Пять элементов – Cr, Fe, Ni, Cu, Zn.

Полное изложение содержания данного примера (таблицы планов, результатов наблюдений,

первичной и основной статистической обработки данных, около 60-ти адекватных и полезных

формул, графики ГФ) могло бы занять в восемь раз больше места, чем изложение предыдущего

примера. Поэтому приведем лишь фрагментарное описание результатов работы.

Для начала закодировали названия определяемых элементов номерами: 1 - Cr, 2 – Fe, 3 – Ni,

4 – Сu, 5 - Zn. Пределы возможных изменений концентраций этих элементов X

- от 0 до 1 мг/л.

Таким образом, область планирования эксперимента - гиперкуб. Предполагали, что структура

градуировочных функций - линейная со взаимодействиями. Для построения этих моделей на

гиперкубе использовали полный факторный эксперимент (ПФЭ) 2

с 8 параллельными опытами в

центре плана. Матрица результатов экспериментов состояла из матрицы плана X и матрицы

наблюдений Y , размерности 40×5 каждая. При построении прямых регрессионных моделей (1.4)

использовали части матриц X и Y , размерности 32×5 каждая (ПФЭ).

При построении обратных моделей (1.5) использовали все 40 опытов, так как опыты,

проведенные в центре плана по переменным Х

не являются параллельными, когда в качестве

регрессоров используются переменные Y

. Часть матрицы Y размерностью 8×9 (опыты в центре

плана) использовались для оценки дисперсий воспроизводимости откликов и проверки

адекватности моделей.

В результате расчета пошаговым методом регрессионного анализа получили зависимости

интенсивностей Y

аналитических линий элементов от их концентраций. Например, для хрома

= 114 X

- 14 Х

+ 35 Х

- 9.5 Х

- 27 Х

+ 11Х

; S

0Y1

= 3 с

-1

;

996.0

Построили регрессионные зависимости концентраций элементов X

от интенсивностей

аналитических линий. Например, для хрома

= 0,63

∗

-2

+ 0,89

∗

-2

+ 0,39

∗

-5

- 0,968

∗

-8

; S

0X1

= 0,05; 99.0

=R .

Гипотеза об адекватности модели регрессии сформулирована в виде конъюнкции двух

гипотез - о равенстве дисперсий остаточной и воспроизводимости и о незначимости квадратичных

эффектов. Только одна модель для никеля оказалась неадекватной. Причина неадекватности

состояла в высокой значимости квадратичных эффектов. Для построения адекватной модели

достроили план эксперимента до плана второго порядка только для никеля, провели

эксперименты и заново выполнили регрессионный анализ с использованием квадратичных

базисных функций.

Получили уточненные модели второго порядка для никеля, которые оказались адекватными

результатам наблюдений. Адекватные ГФ требуют при дальнейшем использовании

вычислительной техники. Для расчетов вручную могут быть использованы менее точные, но

более простые ГФ. Для этого программа регрессионного анализа вывела на печать по 5-6 простых

ГФ для каждого элемента. Простые ГФ, включающие 1-3 переменных были представлены вместе

с доверительными интервалами в виде номограмм.

Нашли, что во всех базисных функциях, вошедших в модели, присутствуют основные

переменные (в модели для X

- переменная Y

; в модели для Y

- переменная X

), то есть не

основные переменные входят только во взаимодействии с основной.

9.5. Задачи будущих исследований

Две задачи остались за рамками настоящего исследования.

9.5.1. Оптимизация методики выполнения измерений

Задача оптимизации МВИ является многокритериальной. Частными критериями

оптимизации могут быть: число опытов в плане градуировочного эксперимента, необходимого

для построения ГФ; время упарки раствора на таблетке; масса вещества, выкристаллизовавшегося

на таблетке; суммарная погрешность МВИ, которая, в свою очередь, складывается из

погрешности измерения интенсивности линий спектра элементов и остаточной погрешности ГФ

(1.2). Возможен также учет стоимости МВИ, важности результатов измерения и других критериев.

Опыт показывает, что ГФ являются, как правило, нелинейными. Для построения

нелинейных ГФ требуется использовать планы 2-го или 3-го порядков с большим числом опытов.

Однако если использовать небольшой интервал варьирования факторов, ГФ можно аппрокси-

мировать линейными функциями. Это позволяет использовать планы 1-го порядка с

небольшим числом опытов! С другой стороны, суммарная погрешность МВИ тем меньше, чем

шире интервал варьирования факторов. Для решения названной задачи

необходимо составить

экспериментально-статистическую модель взаимосвязи переменных, определяющих ка-

чество МВИ.

9.5.2. Диалоговая система на ПЭВМ для построения ГФ.

Как указывалось в п. 2, для планирования градуировочного эксперимента и построения ГФ

требуется участие специалиста в области математической теории эксперимента - АСа. Большую

помощь исследователям может оказать программная диалоговая система для ПЭВМ. Все

основные алгоритмы, необходимые для создания такой системы изложены в предыдущих

разделах. Создание такой достаточно формализованной системы - задача очень сложная и может

стать предметом разработки в будущем.

Заключение

При построении градуировочной функции рентгеновского флуоресцентного анализатора,

используемого для определения содержания тяжелых элементов, в растворе следует учитывать

особенности задачи:

1) возможность независимого варьирования концентрациями компонентов, позволяющую

использовать факторные планы градуировочного эксперимента;

2) наличие обратной задачи планирования эксперимента, предполагающее при

необходимости использование итерационной процедуры планирования эксперимента;

3) наличие обратной задачи оценивания параметров регрессионной модели,

предполагающее при необходимости исключение смещения вектора коэффициентов;

4) наличие одной существенной и ряда менее существенных переменных в моделях,

предполагающее при необходимости достройку плана эксперимента до плана второго порядка

лишь по существенным переменным;

5) необходимость ортогонального планирования эксперимента и расширения разрешающей

способности градуировочной функции для определения концентраций компонентов в наиболее

широком диапазоне отношений концентраций элементов требует расширения области опреде-

ления градуировочной функции до гиперпараллелепипеда, ограниченного нулевыми и

максимальными значениями концентраций определяемых компонентов;

6) в зависимости от выбранного порядка плана используют различные процедуры проверки

адекватности моделей. Для планов первого порядка - с помощью пары нулевых гипотез о

равенстве дисперсий и равенстве нулю суммы квадратичных эффектов. Для планов второго

порядка - с помощью гипотезы только о равенстве дисперсий;

7) простота процедуры использования известных факторных планов заставляет в качестве

исходной структуры градуировочной функции принять линейные (реже - квадратичные)

полиномиальные модели с взаимодействиями.

Задача построения градуировочных функций может иметь несколько решений.

Градуировочные функции могут иметь вид систем уравнений, включающих сложные и точные,

или простые и грубые эмпирические функции регрессии. Градуировочными функциями могут

быть формулы, явно выраженные относительно определяемых переменных. Выбор приемлемой

структуры градуировочных функций является задачей экспертного оценивания.

Литература

1. Методика выполнения измерений для рентгенофлуоресцентного определения содержания хрома,

железа, никеля, меди, цинка, кобальта и свинца в сточных водах с концентрациями больше 0,5 мг/л. //

ВНИИВО. - Харьков, 1989. - 14 с.

2. Лосев Н. Ф., Смагунова А. Н. Основы рентгеноспектрального флуоресцентного анализа. – М.:

Химия, 1982. – 208 с.

3. Любимова С. В. и др. Применение планирования эксперимента для калибровки многоэлементного

рентгенорадиометрического анализатора. - Зав. лаб., № 3, 1979. – С. 252-256.

4. Макулов Н. А. Оптимальные системы стандартных образцов. - Журн. прикл. спектроскопии, т. 26,

вып. 1, 1977. - С. 5-13.

5. Адлер Ю. П., Маркова Е. В., Грановский Ю. В. Планирование эксперимента при поиске

оптимальных условий. - М.:Наука, 1976. -280 с.

6. Рудай А. Н., Цейтлин Н. А., Рудай В. И., Ицков Ф. Э. Разработка рациональных процедур

программы линейного регрессионного анализа // Статистические методы в основной химии: Труды. Т.63 /

НИОХИМ. - Харьков, 1986. - С. 72-84.

7. Денисов В.И. Математическое обеспечение системы ЭВМ-экспериментатор. - М. :Наука, 1977. - 251 с.

8. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. - М. :Наука,

1981. - 544 с.

9. Бард И. Нелинейное оценивание параметров. - М. :Статистика, 1979. - 350 с.

10. Цейтлин Н.А. Применение методов математической теории эксперимента в содовой

промышленности. Обзорная информация. Серия: Содовая пром-сть. - М.:НИИТЭХИМ, 1984. - 36 с.

11. ГОСТ 8.505-84. Метрологическая аттестация методик выполнения измерений содержания

компонентов проб веществ и материалов. - М. :Изд-во Госстандарта СССР, 1984. - 16 с.

12. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. - М. :Наука, 1983. - 416 с.

13. Шеффе Г. Дисперсионный анализ. - М.:Наука,1980. - 512 с.

14. Гординский А.А. Построение регрессионных моделей технологических процессов для целей

управления // ИКА. - 1988. –Вып. 4(68). - С. 64-76.

15. Цейтлин Н.А. Определение верхнего допустимого предела случайной погрешности измерения

технологического параметра при планировании эксперимента // В кн.: Метрологическое обеспечение

измерений параметров состава и свойств веществ и материалов на предприятиях и в организациях

химической промышленности: Труды. Т. 67/ ХНПО "Карбонат". – Харьков, 1988. - С. 167-176.

16. Ицков Ф.Э., Рудай А.Н., Цейтлин Н.А. Построение интерпретируемых регрессионных моделей

технологических объектов // В кн.: Применение математических методов для интенсификации

технологических процессов в производствах основной химической промышленности: Труды. Т. 88/ ХНПО

"Карбонат". - Харьков, 1989. - С. 40-47.

17. Себер Дж. Линейный регрессионный анализ. - М. :Мир, 1980. - 456 с.

18. Цейтлин Н. А. Проверка гипотез методом доверительных интервалов // В кн.: Методы

математической статистики в основной химии: Труды. Т. 55/ НИОХИМ. - Харьков, 1981. - С. 82-89.

19. ГОСТ 24026-80. Исследовательские испытания. Планирование эксперимента. Термины и

определения. - М. :Изд. Стандартов, 1980. - 18 с.