Цейтлин Н.А. Из опыта аналитического статистика

Подождите немного. Документ загружается.

можно получить, решая уравнение (4) относительно х. Однако такое решение не точно и

громоздко. Поэтому аппроксимацию зависимости Х = Х (у, t) необходимо искать отдельно в виде

х =

(t) +

(t)y +

(t)y

(t)|y -

(t)|. (5)

Дело в том, что коэффициенты функций (1) и (5) минимизируют остаточную дисперсию

соответствующего отклика - у или х, то есть они максимально точны в классе выбранных

аппроксимирующих функций (1) или (5).

Итак, методом линейного регрессионного анализа [4] получена вторая аппроксимация

поверхности отклика системы N в виде зависимости (5)

х = 0.346 - 1.43у + 0.1412u + 0.98y

- 0.82uy

+ (0.071u

- 0.591)|у -(0.193 - 0.1u)|. (6)

Все коэффициенты ЭФР (4) и (6) значимы на уровнях значимости, меньших 0.01; остаточное

СО для ЭФР (6) S

x = 0.0032кг/кг на области 0

≤

(t), 0

≤

100°, где y

(t) - растворимость

NaCl в воде (кг/кг).

Аппроксимации линии излома имеют вид

= 0.1020 + 2355и,

= 0.193 - 0.1u. (7)

Для классификации точек ФХС системы N по фазовому признаку разделим область

всевозможных состояний системы на односвязные подобласти по фазовому составу (см. рис.) и

каждой из полученных четырех подобластей присвоим определенный номер.

Используем функцию [2; Р5]

∑

, (8)

где П

- индикаторная П-функция подобласти

Ω

, то есть П

(х) = 1 при x

∈

Ω

, и П

(х) = 0 при

∉

Ω

. Очевидно, что в любой точке ФХС системы функция L принимает значение номера

подобласти, содержащей эту точку. Таким образом, классификация точек ФХС системы сводится

к вычислению значения функции L.

Если

Ω

- одномерная область, то есть

Ω

= (а, b), то

ПП(,,)1,(,);П 0,(,); П ()/(2||)()/(2||).

abxxabxabxaxaxbxb

==∈=∈=−−−−− (9)

В нашей задаче индикаторные функции имеют вид

()()()()

{

}

()()()()()

{}

()()

()

()()

{}

ПП[0,(,),]; ППyx,t П 0,,,,П0,,,;

ПП ,П ,0,,,,П ,1,,;

ПП ,П0,,,П,1,,,|,

yxtytxVxttxy

yxttxtxWxttxy

vxttxWxttxtxy

φφ

==



=



=+−





(10)

где у = V(x, t) и y = W(х, t) - поверхности, разделяющие области 2 - 4 и 3 - 4 соответственно (см.

рис.);

()()()()()()()

,11;,11,

yxyx

VxtxttWxtxttφφφφ



=−+=−−





(11)

где φ

(t), ψ

(t) - функции (7), описывающие линию излома поверхности отклика; у(х, t), х(у, t) –

аппроксимации (4) и (6) поверхности насыщения.

Пример «чтения» функций (8) - (10) можно найти в опубликованной ранее работе [5] (см.

также [Р6.1.1]).

Литература

1. Справочник экспериментальных данных по растворимости солевых систем. / Под ред. А. Д. Пельша.

- Л.: Госхимиздат, 1973. - Т. 1, кн. 1. – 568 с.

2 Э. Н. Авраменко, Ф. С. Новик, Н. А. Цейтлин. ЖПХ, LIV, 2053 (1981).

3. Э. Я. Тарат. ЖПХ, LIII, 2710 (1980).

4. Г. Н. Девяткова. // В сб. «Регрессионные эксперименты (планирование и анализ)». / Под ред. В. В.

Налимова. - М.: Изд. МГУ, 1977. – 212 c.

5. Ф. С. Новик, Н. А. Цейтлин, Э. Н. Авраменко. ЖНХ, 26, 756 (1981).

6.5.2. Аппроксимация физико-химического состояния системы CaCl

-NaCl-H

Цитируется одноимённая работа [Eдвабник И. Ю., Цейтлин H. А. // Вопр. химии и хим.

технологии. - 1987. - Вып. 83. - С. 40 – 43]

Изотермы растворимости системы CaCl

-NaCl-H

O в интервале температур 0 – 100

состоят из двух ветвей кристаллизации - NaCl и кристаллогидратов CaCl

(CaCl

⋅

O) [1]. Эти

изотермы являются кусочно-гладкими кривыми с одной точкой излома (рис.).

Рисунок. Изотермические сечения диаграммы растворимости тройной системы CaCl

-NaCl-Н

х, у - концентрации NaCl и CaCl

в системе, кг/кг.

Быстрые методы решения задач аппроксимации физико-химического состояния (ФХС)

тройных систем развиты в работах [2 – 4; Р6.1; Р6.5]. Формулы для апроксимации ФХС системы

С будем искать в виде сплайн-функций:

y = y(x, t) = I

(

(t) +

∆

; x)

⋅

(x, t) + y

(x, t); (1)

x = x(y, t) = I

(φ

(t) + ∆; y)⋅x

(y, t) + x

(y, t), (2)

где x, y - концентрации СаСl

и NaCl соответственно, кг/кг; t - температура системы,

С;

(t) -

координаты точек излома изотерм (эвтонических точек); I

(а; x), I

(a; х) - единичные

ступенчатые функции;

(

)

(

)

1010

;1,;;0,;

IaxxaIaxxa

=<=>

(

)

(

)

0101

,0,;,1,;;

IaxxaIaxxaxa

=<=>≠

(3)

Δ > 0 - малое число (Δ = 10

-5

), введенное для практического устранения неопределенности

функций у(х, t) и x(y, t) вдоль линии излома [3].

Аппроксимация ФХС одной и той же системы С двумя функциями (1) и (2) связана с

необходимостью повышения точности и упрощения технологических расчетов [4].

Очевидно, что при x < φ

(t) + Δ, у > φ

(t) + Δ функции

y(x, t) = y

(x, t) + y

(x, t); x(y, t) = x

(y, t) + x

(y, t), (4)

а при x > φ

(t) + Δ, у < φ

(t) + Δ -

y(х, t) = y

(х, t), x(y, t) = x

(y, t). (5)

Значит, функции (4) аппроксимируют поверхность насыщения по NaCl, а функции (5) -

поверхность насыщения по CaCl

⋅

nН

О.

Условия стыковки поверхностей насыщения вдоль линии изломов имеют вид

(

(t) + Δ, t) = x

(

(t) + Δ, t) = 0. (6)

Зависимость координат эвтонических точек аппроксимировали формулами

(t) = 0,0059 - 0,0051u + 0,0103u

; u = t/100; (7)

(t) = 0,4495 + 0,19u + 0,086⋅|u - 0,25| - 0,204⋅|и - 0,5|. (8)

Полиномиальная аппроксимация

(t) имела большую погрешность. Гораздо точнее эта

зависимость аппроксимируется кусочно-линейной функцией (8) [3].

Поскольку на каждой изотермической кривой насыщения по CaCl

⋅

O лежит всего по две

точки с координатами (

) и (X

, 0), где X

- растворимость СаСl

⋅

nН

О в бинарном растворе, то

функции у

(х, t), х

(у, t) будем искать в виде

(х, t) = B

(t) + B

(t)x; (9)

(у, t) = A

(t) + A

(t)y, (10)

(t) = β

+ β

t + β

; (11)

(t) = α

+ α

t + α

, 1,0=i . (12)

Аппроксимация поверхности насыщения по NaCl полиномами высоких порядков имеет

большую погрешность. Это связано с различным характером крутизны отдельных участков этой

поверхности (см. рис.). Поэтому зависимости у = у

(x, t) и x = x

(y, t) искали в виде сплайн-

функций дефекта 2 с двумя узлами c

, c

и d

, d

соответственно [5]:

()()()

(

)

()()()

323

1010

111

jxijii

jij

yxtBtxtBtxcIcx

===

=−+−

∑∑∑

; (13)

()()()

(

)

()()()

323

1001

111

jyijii

jij

xytAtytAtydIdy

===

=−+−

∑∑∑

, (14)

(t) = b

+ b

t + b

; (15)

(t) = a

+ a

t + a

, 2,1=i , 3,1=j . (16)

Функции (13) - (16) линейны по всем параметрам, кроме с

, c

и d

, d

соответственно.

Совместное оценивание всех параметров выполнили с использованием программы линейного

регрессионного анализа, варьируя параметры с

, c

и d

, d

по не композиционному плану второго

порядка [6]. Минимумы остаточных CO ошибок аппроксимации обеспечиваются ЭФР

у(x, t) = 2,116(x - 0,2)

(0,2; х) + [1,311(х - 0,35)

- 0,2853(х - 0,35) - 0,242u(х -

- 0,35)

]

⋅

(0,35; х) – 0,0686u(x -

(t))I

(

(t); x) + 0,01804 - 0,0352x + 0,0081u; (17)

x(y, t) = -11,81(у - φ

(t))I

(φ

(t); y) + [4,6(у - 0,02) + 13,25u(у - 0,02)]I

(0,02; у) +

+ 0,779(у - 0,08)I

(0,08; у) + 0,354 + 5,42y + 0,396u - 0,1032u

- 13,54yu. (18)

Все полученные коэффициенты регрессии значимы на уровнях значимости, меньших 0,01;

остаточные CO для формул (17), (18) равны, соответственно, S

= 0,25

⋅

-2

кг/кг и

= 0,19⋅10

-1

кг/кг; максимальные невязки откликов равны

max0,006;max0,049

yx∆=∆=

на области 0

≤

100°C, 0

≤

(t); 0

≤

(t), где x

(t), y

(t) - растворимость в воде

компонентов CaCl

⋅nН

О и NaCl, соответственно, кг/кг [1].

ЭФР (17), (18) позволяют легко классифицировать точки ФХС системы С по фазовому

признаку точно так, как это сделано в работе [4] (см. выше [Р6.5.1]) для солевой системы NH

Cl-

NaCl-H

O. Обозначения на рисунке соответствуют обозначениям в [4; Р6.5.1]: «1» -

ненасыщенный раствор; «2» - раствор, насыщенный по NaCl, и кристаллы NaCl; «3» - раствор,

насыщенный по CaCl

⋅nH

O, и кристаллы CaCl

⋅nH

O; «4» - кристаллы NaCl и CaCl

⋅nH

(деление по фазовому составу (1 - 4) условно выполнено для температуры 100

C). y = v(x, t) -

уравнение конической поверхности, проходящей через полюс кристаллизации NaCl с

координатами (0,1) и кривую излома (

(t),

(t)); y = w(x, t) - уравнение поверхности, проходящей

через кривую излома (φ

(t), φ

(t)) и полюс кристаллизации CaCl

⋅nH

O с координатами

((1 + 0,162n)

-1

, 1).

Литература

1. Справочник экспериментальных данных по растворимости солевых систем / Под ред. А. Д. Пельша. -

Л.: ГОНТИ, 1973, 1, кн. 1. - 568 с.

2. Э. H. Авраменко, Ф. С. Новик, H. А. Цейтлин. Кусочно-гладкая аппроксимация поверхности отклика

и диаграмм состояния/ Журн. прикл. химии. - 1981. – 54, № 9. - С. 2053 - 2056.

3. Ф. С. Новик, H. А. Цейтлин, Э. H. Авраменко. Некоторые способы кусочно-гладкой аппроксимации

функций / Зав. лаб. - 1981. - № 1. - С. 48 - 55.

4. H. А. Цейтлин, T. В. Можарова, И. Ю. Едвабник. Аппроксимация физико-химического состояния

системы NH

Cl-NaCl-H

O / Журн. прикл. химии. -1983. - № 12. - С. 2732 - 2734.

5. Ю. С. Завьялов и др. Методы сплайн-функций. M.: Наука, 1980. - 352 с.

6. Э. Я. Тарат, H. А. Цейтлин и др. Исследование гидравлического сопротивления опорных решеток со

взвешенной насадкой разного типа // Журн. прикл. химии. - 1980. - 53, № 12. - С, 2710 - 2714.

7. Экспериментальная оптимизация. Технология полимеров. Поиск оптимального состава

наполненных эпоксидно-каучуковых композиций для химически стойких покрытий

Увлекающийся практикой без науки - словно кормчий,

вступающий на корабль без компаса. (Леонардо да Винчи)

Уже давно, со времён основоположника теории планирования эксперимента, Р. Фишера

[16] известно (к сожалению, не всем), что рационально поставленное экспериментальное

исследование начинается с его оптимального планирования (рекомендуется сначала

заполнить опросный лист исследователя - [Р11]). Однако нередко бывает иначе.

В одноименной работе (Штода В. Л., Едвабник И. Ю., Цейтлин Н. А. - Деп. рукопись

№256-ХII-88 НИИТЭХИМ, 09.03.88 г., г. Черкассы, 1988 г. 36 с.) описана типичная, к сожалению,

ситуация, когда исследователь (в данном случае – первый из соавторов) приходит к

аналитическим статистикам с готовыми результатами дорогих и длительных, не оптимально

спланированных экспериментов, и просит о помощи: «поставить и решить задачу

многокритериальной оптимизации…»

При решении данной задачи авторы не смогли отойти от укоренившейся в среде

математиков традиции, которую проще всего проиллюстрировать так. Если математику

ставят задачу определить устойчивость стола на четырёх ножках, он формулирует её в общем

виде, когда число ножек

, а затем рассматривает частные случаи, когда

n = 1, 2, 3, и т. д

.:-).

Введение

В литературе имеются отрывочные сведения [1, 2] о том, что параметры физических

свойств эпоксидных композиций марки ЭД-20 улучшаются при добавлении в смесь

олигоизопрендигидразида (ОИГ). Так, в работе [1] исследовано влияние ОИГ на износ деталей;

в [2] – на удельную ударную вязкость.

Целью настоящей работы было экспериментальное исследование влияния одного фактора

Х – концентрации ОИГ в исходной смеси на основные физические свойства композиций:

прочность при растяжении Y

, внутреннее напряжение Y

, удельную ударную вязкость Y

удельную поверхность раздела фаз Y

и износ Y

, а также оптимизация указанных свойств.

Для экспериментов взяли чистую смолу марки ЭД-20 (ГОСТ 10587-76), использовали

алифатический амин полиэтиленполиамин (ПЭПА), ТУ 6-02-594-70 и применяли жидкий каучук

ОИГ, ТУ 38-104406-82.

Композиции с ОИГ получали (табл. 1) смешением компонентов следующим образом: к

эпоксидному олигомеру при комнатной температуре или при нагревании до ~40

С добавляли

ОИГ, тщательно перемешивали, добавляли наполнитель и после перемешивания добавляли

растворитель.

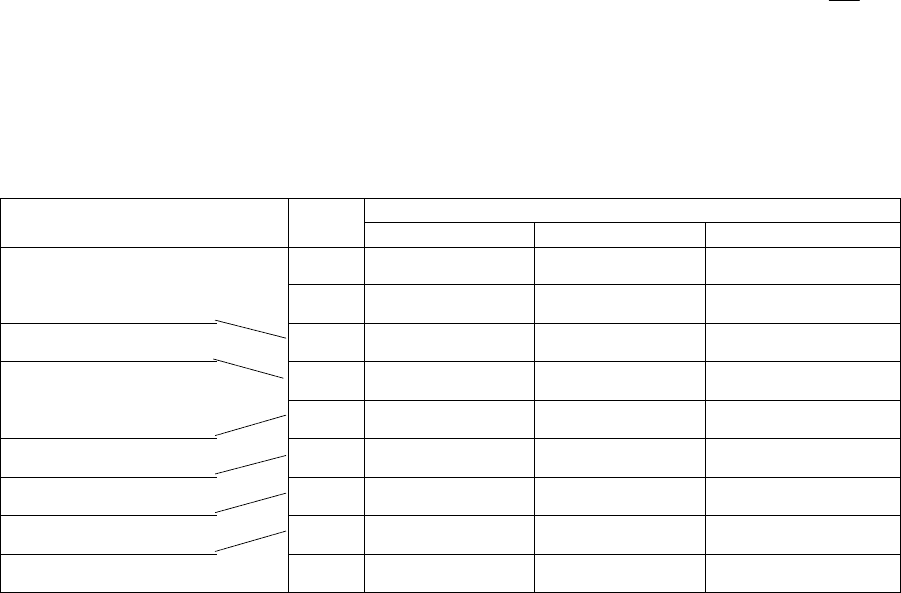
Таблица 1

Результаты экспериментального исследования зависимости параметров физических

свойств эпоксидной композиции от концентрации ОИГ

Параметры физических свойств смолы

Х*

Прочность при

растяжении, Y

, мПа

Внутреннее нап-

ряжение, Y

, мПа

Уд. ударная вязкость,

, кг⋅с⋅см/см

Уд. поверхн. раз-

дела фаз, Y

, м

/см

Износ, Y

0 -

6,03; 6,48; 7,15;

7,68; 8,45

4,68; 5,18; 5,36; 5,95;

6,12

28,7; 33,0;

36,5

58,4; 63,4; 68,8; 71,5;

75,0

6,35; 6,88; 7,26; 7,71;

8,45

- -

78,8; 82,5; 88,7; 94,3;

100,1

- - 0,018; 0,036; 0,042 -

3 -

2,11; 2,33; 2,45;

2,55; 2,74

6,61; 7,15; 7,54; 8,07;

8,68

19,0; 20,2;

21,6

76,0; 80,5; 85,2; 90,3;

95,2

1,87; 1,98; 2,18;

2,28; 2,36

7,04; 7,55; 8,24; 8,78;

9,36

0,059; 0,065; 0,083

20,6; 18,7;

21,6

60,5; 64,7; 70,4; 73,8;

78,0

1,52; 1,68; 1,75;

1,83; 2,02

7,34; 7,98; 8,67; 9,42;

9,82

0,082; 0,068; 0,090

19,2; 18,4;

22,0

* Примечание.

– массовая концентрация ОИГ в смеси, г на 100 г ЭД-20.

Аминный отвердитель вводили в охлажденную смесь перед применением в

стехиометрическом соотношении, учитывая, что часть эпоксидных групп взаимодействует с

гидразидными группами ОИГ. Образцы для сорбционных испытаний диаметром 20 мм и

толщиной 1,5 мм получали методом заливки в специальную металлическую форму,

предварительно смазанную разделительным слоем из раствора каучука СКТ в толуоле. После

выдержки при комнатной температуре в течение 20 – 24 ч производили термообработку образцов

при 100

С в течение 8 ч и после охлаждения извлекали из формы [1].

Физические свойства определялись 3-5 раз по следующим методикам [1].

Определение деформационно-прочностных свойств проводили на разрывной машине МР-

05-1 в соответствии с ГОСТ 18299-72. Скорость деформации пленок 90 мм/мин, толщина образцов

составляла 0,15 – 0,25 мкм.

Внутреннее напряжение в покрытиях определяли консольным методом по ГОСТ 13036-67.

Удельную ударную вязкость определяли на маятниковом копре по ГОСТ 4647-80. Размер

образцов 10х15х120 мм.

Гетерофазность композиционных материалов контролировалась при помощи оптического

микроскопа МБИ-6.

Абсолютная удельная поверхность раздела фаз определялась по формуле Y

= 4Z/L, где Z -

число отрезков, соответствующих сечениям дисперсной фазы на всех случайных секущих линиях;

L - общая длина секущих, мкм.

Уровни варьирования фактора Х (см. табл. 1) устанавливали так, чтобы их было много

(Типичная ошибка многих экспериментаторов! – Н. Ц.).

Сформулируем теперь три содержательные задачи.

Первая задача. Проверить предположения о том, что пять параметров физических свойств

– Y

) зависят от концентрации ОИГ в смеси. Если такая зависимость будет установлена, то

второй задачей

будет подбор вида аппроксимирующей функции для каждого параметра.

Третьей задачей является поиск такой компромиссной почти стационарной области

концентрации ОИГ, в которой бы все механические свойства смолы были наилучшими: величины

, Y

- наибольшими; Y

, Y

- наименьшими.

7.1. Подбор вида аппроксимирующей функции

Первую задачу для каждого отклика Y

можно сформулировать следующим образом.

Имеется т выборок

{

}

(

)

jij

wYjm

== равных объемов по N элементов каждая (см.

табл. 1) из множеств значений случайной величины Y , распределенной по нормальному закону с

параметрами – математическим ожиданием ϕ(х

) и дисперсией

. Опыты спланированы так, что

в каждой точке фактора х

плана (

), принадлежащей области

Ω

действия величины

х: х

∈Ω

(

{}{}

{

}

min,max

xxR

Ω=⊂

) выполнено по N параллельных измерений величины Y.

Необходимо:

1) Оценить дисперсию случайной величины Y.

1. 1) Получить оценку дисперсии величины Y в каждой точке х

плана.

1. 2) Проверить гипотезу о равенстве дисперсий на множестве точек плана.

2) Проверить гипотезу о постоянстве математического ожидания

(х) отклика

: ϕ(х) = const (1.1)

против альтернативной гипотезы Н

о его непостоянстве H

: q(x) = var.

В случае, если гипотеза Н

(1.1) отклоняется, необходимо:

1) Подобрать вид функции регрессии

(х).

2) Проверить гипотезу об адекватности аппроксимирующей функции ϕ(х)

экспериментальным данным.

В случае успешного решения задач по п. 1 и 2 (отклонения гипотезы Н

(1.1) и

адекватности функции ϕ(х)) будет поставлена статистическая задача оптимизации.

Решение.

1) По данным табл. 1 вычислим (табл. 2) несмещенные оценки

[3] дисперсий величин

в точках х

плана (

= ).

2) Гипотезу об однородности дисперсий

, полученных по результатам наблюдений (см.

табл. 2), проверим α-методом [4; Т2Р1]. В прикидочных опытах можно принять критический

уровень значимости [4] α

к0

= 0,01. Вычислим статистику Фишера-Бонферрони [Ф(51)Р1]

{

}

{

}

2222

,,/(2)

max,min,

frfzlijij

FSSSS

= , (1.2)

где f

= f

и f

= f

, если

или f

= f

и f

= f

, если

Таблица 2

Статистические характеристики распределения параметров физических свойств

композиции на основе смолы ЭД-20 по данным табл. 1

)

Число параллельных опытов, N 5 5 5 3 3

Число групп, m 4 4 5 3 4

СО ошибки воспроизводимости, S

1,53 0,51 0,84 0,01 2,38

Число f

степеней свободы для S

16 16 20 6 8

Статистика Фишера-Бонферрони,

()

,,/2

frfzl

1,71 2,7 2,99 1,29 9,05

Уровень значимости по

()

,,/2

frfzl

→

>0,3 0,037 >0,3 >0,3 0,3

Плечо доверительного интервала, d 7,86 0,53 0,9 0,01 3,6

СО остаточной ошибки, S

0,29 0,067 0,62 0,0098 2,2

Число f

степеней свободы для S

1 1 2 1 1

Критерий однородности дисперсий

→

0,007 0,086 2,72 4 2,56

Уровень значимости по

, α

→

0,933 0,78 0,0098

0,092 0,165

)

Обозначения переменных Y

приведены в табл. 1.

Далее вычислим соответствующий уровень значимости

()

ˆˆ

112

αα

=−− , (1.3)

где

- оценка уровня значимости для одной односторонней альтернативы (вычисляется по

формулам Сливняка и Полсона [4; Ф(19),(20)Р1];

(1)/2

lCmm==−

- число альтернативных

гипотез о неоднородности дисперсий. Число 2 в формуле (1.3) означает, что альтернативные

гипотезы двусторонние. Для практических расчетов используется аппроксимация функции (1.3)

ˆˆ

αα

, справедливая при

< 0,3. (1.4)

Поскольку дисперсии во всех рассматриваемых случаях однородны (все оценки

αα

см. табл. 2), получили средние оценки

дисперсий воспроизводимости откликов [3] (в табл. 2

приведены среднеквадратические отклонения (СО) S

; индексы

1,5

i =

опущены).

Гипотезу о постоянстве функции регрессии проверяли с помощью метода доверительных

интервалов [5; Р2.1]. Для этого на графике (рис. 1) изобразили т интервальных оценок для ϕ(x

)

(

= ). Значение плеча доверительного интервала вычисляли по формуле [5; Ф(21)Р1.2.1]

()

0,5

mfl

dStN

−

= (1.5)

с критическим уровнем значимости

к1

= 0,05, где

()

mfl

- значение верхнего

/(2l) – предела

распределения Стьюдента с mf

степенями свободы.

Поскольку проекции на оси ординат (откликов) всех пар доверительных интервалов (рис.

1) не перекрываются, то для всех пяти откликов гипотезы (1.1) были отклонены. Это позволило

перейти ко второй задаче.

2) Аппроксимирующие функции искали в классе полиномов, а затем проверяли

адекватность найденных аппроксимаций.

2.1) Сначала пытались аппроксимировать данные линейными функциями. Интервальные

оценки для ϕ(x

) в точках x

(

), изображенные на графике (рис. 1), позволили

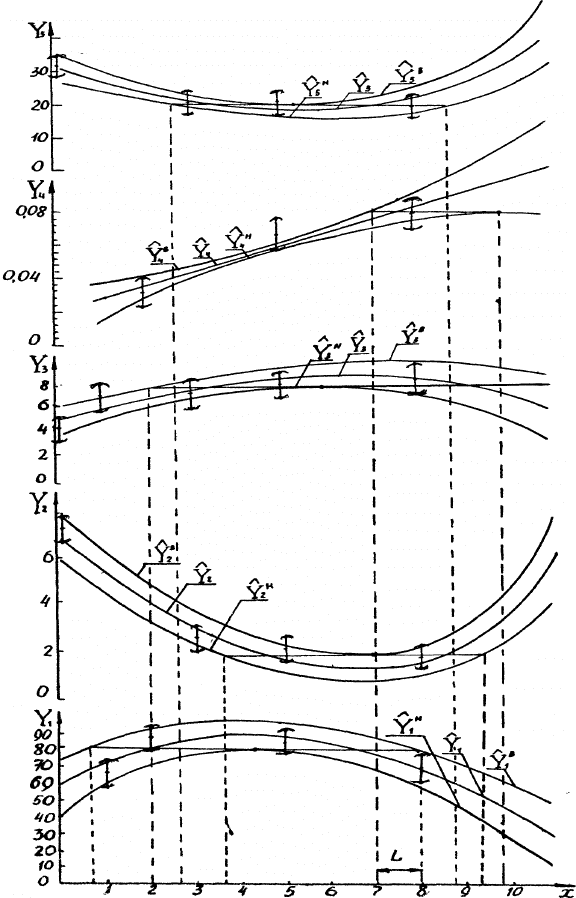
воспользоваться для этого модифицированным методом натянутой нити [3; Р3]. Если натянутая

нить располагается над графиком так, что она накрывается всеми доверительными интервалами

одновременно, то данные можно аппроксимировать линейной функцией. Удачную линейную

функцию получили только для отклика Y

(

)

= 0,02 + 0,008х; (1.6)

функции Y

(х), Y

(х) пришлось аппроксимировать параболами второго порядка

(

)

= 5,91 + 0,77х – 0,055х

; (1.7)

(

)

= 32,32 – 4,71х + 0,4х

. (1.8)

Рис. 1. Зависимость параметров физических свойств (Y

) эпоксидной смолы ЭД-20 от

концентрации (х) олигоизопрендигидразида (ОИГ) в смеси:

x – концентрация ОИГ в смеси, массовые части на 100 массовых частей ЭД-20; Y

– прочность при

растяжении, мПа; Y

– внутреннее напряжение, мПа; Y

– удельная ударная вязкость, кГс⋅см/с

; Y

– удельная

поверхность раздела фаз, м

/см

; Y

– износ, %;

- точечная оценка функции регрессии;

- нижняя

и верхняя границы 95%-ного доверительного интервала для функции регрессии; значения откликов в точках

плана представлены интервальными оценками; горизонтальными и вертикальными пунктирами

представлены построения почти стационарных областей локальных экстремумов, пересекающихся в

области L = {x: 7

≤

8}.

Для адекватной аппроксимации функций Y

(х) и Y

(х) воспользовались нелинейным

преобразованием фактора х вида

u = lg(x + 0,1). (1.9)

Логарифмировать величину х необходимо было, чтобы «сжать» кривые справа, а

коэффициент 0,1 прибавить, чтобы избавиться от нуля под знаком логарифма. В итоге получили

следующие функции:

(

)

= 62,78 + 120,8 u – 125 u

, 1 ≤ х ≤ 8; (1.10)

(

)

= 3,61 – 2,74 u + 0,8 u

. (1.11)

Для расчета коэффициентов в формулах (1.6 – 1.11) пользовались стандартной программой

метода наименьших квадратов [3], которая дает СО остаточной ошибки по формуле

()

(

)

0,5

Yii

SYYmq

′

=−−

∑

, (1.12)

где

- расчетное значение отклика; q – число коэффициентов в аппроксимирующих функциях.

Однако несмещенная оценка СО остаточной ошибки вычисляется по формуле [6]

()

0,5

Yii

SNYYmq



=−−





∑

. (1.13)

Поэтому для пересчета из

′

в S

использовали формулу

0,5

00YY

SSN

′

= . (1.14)

Интервальные оценки функций регрессии

ˆˆ

,,1,5

YYj=

на рис. 1 были построены с

помощью известных [15, с. 338] формул (индекс j опущен):

()

(

)

00,/2

ˆˆˆˆˆ

; ; ;

YYYYYYYSxxxxt

−

′′

=−∆=+∆∆=

(

)

0,5

0000

; ; ,

YYYY

SSfSffffffmq

=+=+=−

где

∆

- плечо доверительного интервала для функции регрессии; S – средневзвешенная оценка

СО отклика с f степенями свободы; х

– вектор факторов [для линейной модели (1.6)

′

= (1; х); для

квадратичных

′

= (1; х; х

)]; х – матрица плана; α = 0,05; остальные переменные расшифрованы

выше. Оценки

построены с помощью специальных таблиц [3].

2.2) Адекватность полученных эмпирических функций регрессии (ЭФР) была

установлена α-методом [3; Р1]. Вычисляли статистику Фишера

,,0

ffYY

FSS

(1.15)

и соответствующий уровень значимости

(см. табл. 2). Поскольку для всех откликов

αα

то гипотезы об адекватности полученных ЭФР не отклонили.

Полученные зависимости позволяют перейти к следующей задаче.

7.2. Многокритериальная оптимизация

Названная задача имеет следующие особенности.

1. Требования к тем или иным (по физической природе) параметрам оптимизации

выдвигаются экспертами, специалистами в предметной области и поэтому являются

субъективными.

Для формализации этих требований необходимо использовать процедуру экспертного

оценивания – прием, позволяющий перенести мнения экспертов о качестве параметров

физических свойств на множество соизмеримых действительных чисел - экспертных оценок

качества (в баллах).

2. Оптимизируемыми является ряд противоречивых критериев оптимизации (оптимум по

одному критерию, как правило, не является оптимумом по другому критерию).

Одним из методов решения этой задачи является сведение ее к однокритериальной.

3. Оптимизируемые параметры физических свойств являются случайными величинами с

постоянной дисперсией и математическими ожиданиями, являющимися функциями факторов.

4. Искомый оптимум, если он существует, может быть не единственным: решением задачи

многокритериальной оптимизации может быть компромиссная область, являющаяся пересечением

почти стационарных участков экстремумов по разным критериям.

7.3. Аналитическое представление обобщенного параметра оптимизации

Одним из методов решения задачи оптимизации по многим частным критериям

оптимизации (ЧКО) является метод сведения ее к задаче оптимизации по одному критерию. Для

этого из многих ЧКО конструируется один обобщенный критерий оптимизации (ОКО).

Удачная конструкция такого ОКО в значительной степени определяет качество решения

задачи. При конструировании ОКО необходимо учитывать мнения экспертов о качестве каждого

ЧКО. В этом случае эксперт становится как бы «измерительным инструментом», с помощью

которого можно «измерить» такие не поддающиеся иному инструментальному измерению

показатели качества как «удобство», «технологичность», «важность», «перспективность» и т. п.

Если мнение эксперта о качестве процесса или продукции удастся формализовать, то есть

привести к аналитическим выражениям, то для решения задачи многокритериальной оптимизации

можно будет применять известные математические методы [7].

Существует большое количество конструкций ОКО (см., например, обзоры [9, 10]).

Наиболее рациональной представляется идея, согласно которой все ЧКО Y

(

) с

помощью некоторого преобразования, приводятся к безразмерным оценкам качества (БОК)

ЧКО. Шкала БОК ЧКО относится к психофизическим шкалам. Её назначением является

установление соответствий между физическими величинами ЧКО и субъективными

психологическими параметрами БОК ЧКО.

Введем в рассмотрение три подмножества ЧКО (табл. 3).

Таблица 3

Оценки качества частных критериев оптимизации (ЧКО)

Значения ЧКО Y

из подмножеств

Оценка качества ЧКО

Баллы

А В С

∧

iiB

∧

iAiiB

YYY

∧∧

Отлично

iiA

∧

iiB

∧

iAiAiBiB

YYYY

∧∧

Хорошо 1

iAiB

Удовлетворительно 3

iAiB

Плохо 4

iAiB

Очень плохо 5

iAiB

Предельно плохо 6

iAiA

iBiB

iAiAiBiB

YYYY

Неприемлемо

iiA

iiB

iiAiiB

YYYY

Подмножество А включает такие ЧКО Y

, увеличение которых соответствует улучшению

свойств объекта. Подмножество В включает такие ЧКО Y

iВ

, увеличение которых соответствует

ухудшению свойств объекта. Наконец, подмножество С включает такие ЧКО Y

iС

, которые для

улучшения свойств объекта следует приводить к некоторой единственной норме.

Предлагается функцию БОК ЧКО строить так, чтобы она представляла собой кусочно-

линейную функцию ЧКО.

Пусть V

= V

) – кусочно-линейная функция, устанавливающая соответствие между

значениями ЧКО Y

и оценкой качества V

, причем V

≥

Применяемые значения ЧКО делятся на шесть подобластей, каждая из которых

оценивается в баллах согласно табл. 3. Функция V

) строится таким образом (табл. 3), чтобы

наилучшим значениям ЧКО

iAi

∧

≤

iiB

∧

≤

соответствовало значение V

= 0, для приемлемых

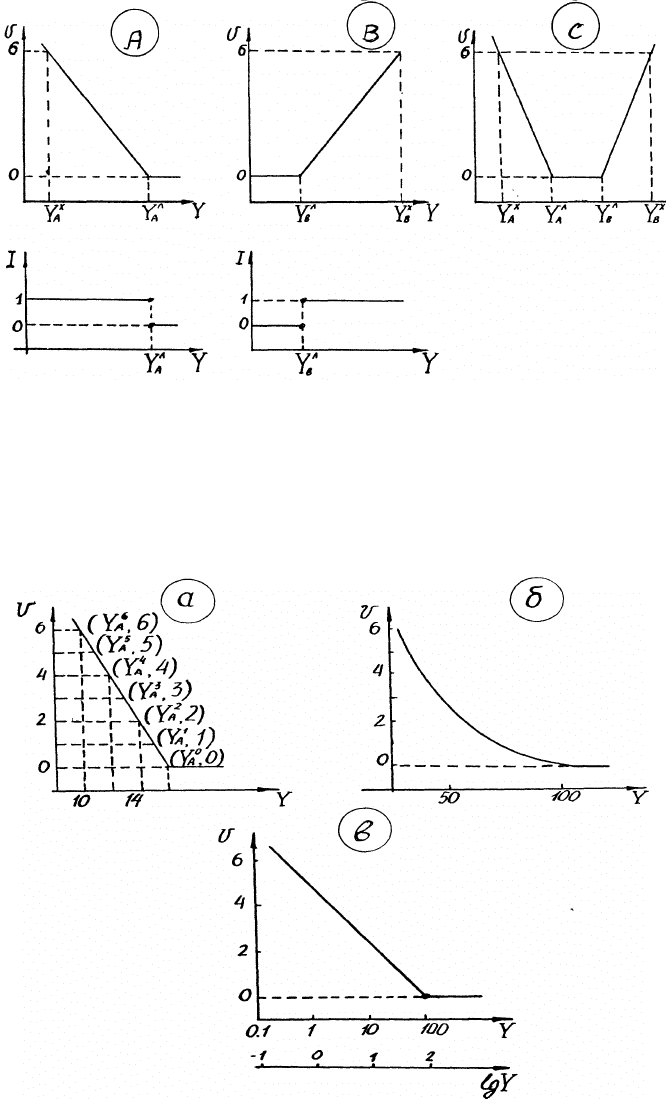
значений

iAiiA

YYY

∧

≤≤

;

iBiiB

YYY

∧

≥≥

: 0 ≤ V

≤ 6 (верхний индекс «^» при Y

означает «лучшее»,

«Х» – «худшее»). В области неприемлемых значений ЧКО оценка V

Для построения функции V

) рекомендуется следующая последовательность действий.

На графике (рис. 2) в координатах Y

– V

наносятся две точки, например, худшая (

, 6) и лучшая

(

∧

, 0) и соединяются прямой.

Рис. 2. Кусочно-линейная аппроксимация оценки качества V - значения частного критерия

оптимизации:

обозначения: А, В, С, V, и т. д. см. в табл. 3; I - вспомогательные единичные ступенчатые функции (3.1.4) и

(3.1.5).

Затем эксперт рассматривает промежуточные оценки значений ЧКО, Он должен

определить, соответствует ли полученное распределение оценок (

, 1), (

, 2) и т. д. (см. табл. 3)

сложившимся в данной предметной области представлениям о качестве ЧКО (см. рис. 3а).

Рис. 3. Примеры построения кусочно-линейной (а) и логарифмической кусочно-линейной

(б, в) аппроксимаций качественной оценки V значения частных критериев оптимизации Y.

Если такого соответствия нет, эксперт наносит на графике новые промежуточные точки