Цейтлин Н.А. Из опыта аналитического статистика
Подождите немного. Документ загружается.

3
3. Методические указания к лабораторным работам по курсу «Поиски и разведка
месторождений полезных ископаемых» / ХГУ. - Харьков, 1987. - 85 с.
4. Закс Л. Статистическое оценивание. - М.: Статистика, 1976. - 598 с.
5. Цейтлин Н. А. Применение методов математической теории эксперимента в
содовой промышленности: Обзор. информ. Сер. Содовая пром-сть. - М.: НИИТЭХИМ,
1984. - 36 с.
6. Хованский П. С. Основы номографии. - М: Наука, 1976. - 352 с.
7. Цейтлин Н. А. Методы статистической обработки результатов наблюдений при
пылогазовых замерах / НИОХИМ. – Харьков, 1981. - 53 с. - Деп. в ОНИИТЭХИМ г.
Черкассы 7.08.81, № 725 ХП-Д 81.
1
3.11. Применение быстрых и машинных статистических методов обработки данных.
Технология полимеров. Исследование механических свойств эпоксидных
композиций
Талант руководителя состоит в том, чтобы быстро принять решение и найти человека,
который сделает всю работу. Дж. Г. Поллард.
Статистическая обработка результатов наблюдений в задачах с малым числом
варьируемых переменных часто включает графическое представление поверхности отклика, её
аналитическую аппроксимацию и поиск экстремума функции отклика. Эти цели могут быть
достигнуты быстрыми и машинными методами статистической обработки данных. Под
быстрыми подразумеваются методы обработки [1, с. 3; 2, с. 7; 3] с использованием
простейших средств оргтехники - линейки, лекала и сплайна для построения графиков,
микрокалькуляторов для расчета коэффициентов уравнений; машинными являются сложные
аналитические методы (многомерный регрессионный анализ [4, с. 294], интерполяция сплайнами
[5], оптимизация [6, с. 3] и т. п.), требующие для своей реализации применения ЭВМ.
В одноимённой работе (Цейтлин Н. А., Фарберов А. С., Прилуцкая Н. В., Едвабник И. Ю.,
Ланцберг Н. Г. Лакокрасочные материалы и их применение № 6, 1986, с. 21-24) описана
типичная, к сожалению, ситуация, когда исследователи (в данном случае – второй и третий из
соавторов) приходят к аналитическим статистикам (АСам) с готовыми результатами дорогих
и длительных, не оптимально спланированных экспериментов и просят о помощи: поставить и
решить задачу многокритериальной оптимизации, причём «ВСЁ надо сделать очень
быстро»!…
Нашим АСам удалось справиться с задачей. Пришлось сымпровизировать быстрый метод
нелинейной графической интерполяции для изображения поверхности отклика и
интервальной оценки экстремума функции регрессии, или, коротко, метод статистического
контурно-графического анализа.
После сдачи готовой работы в установленный срок, АСы (уже не спеша) показали, что
быстрые и машинные методы статистической обработки данных в задачах с малым числом
варьируемых переменных приводят практически к одинаковым результатам.
Для аналитического описания сложной поверхности отклика применили интерполяционную
формулу Смоляка [5].
Исходными данными для обработки являются результаты исследования механических
свойств эпоксидных композиций (ЭК). Для повышения эластичности плёнок, используемых для
защиты от коррозии оборудования химических производств, применяют различные
модификаторы, в частности моноэпоксиэфир жирных кислот таллового масла (МЭЭ).
Введение его в композицию позволяет повысить прочность пленки на растяжение по сравнению с
непластифицированным материалом [7].
Значительный интерес представляет использование МЭЭ в качестве внутреннего
пластификатора ЭК, отверждаемых ангидридами, и предназначенных для получения
толстослойных плёнок и изготовления деталей химического оборудования.
В описываемой работе исследовали ЭК, содержащие эпоксидный олигомер ЭД-16 (X
3
);
диабазовую муку (наполнитель, X
1
); МЭЭ (X
2
); фталевый ангидрид (0,6 X
3
); тиксотропную добавку
аэросила A-175 (0,05 X
3
) и для ускорения отверждения – «белую сажу», модифицированную
моноэтаноламином (0,05 X
3
).
Эффективность пластифицирующего действия модификатора в исследуемых толстослойных
плёнках оценить обычными методами определения эластичности плёнок [7] не удается, так как
чувствительность этих методов невелика.
В связи с этим проводили определение ударной вязкости (Y
2
) на маятниковом копре типа
WPM и разрушающего напряжения при изгибе (Y
1
) на разрывной машине типа ЧММ-5 (ГОСТ
7855-01).
Для механических испытаний готовили по 4 - 5 образцов. Средние значения откликов
сведены в табл. 1 (Y
3
- функция желательности).
2
Статистическая обработка результатов наблюдений (из табл. 1) заключалась в
следующем:
1) проверка однородности дисперсий ошибок измерения откликов в опытах (с помощью
α
-
метода проверки статистических гипотез [8; Р1]) и усреднение однородных дисперсий;
2) построение зависимости прочностных свойств (откликов Y
1
и Y
2
) от независимо
варьируемых факторов X
1
и X
2
, Y
i
= f
i
(X
1
, X
2
),
2,1=i
;
3) построение почти стационарной области экстремума
ω
, в которой прочностные свойства
являются наилучшими, а именно:
3.1) формулирование комплексного показателя качества Y
3
- функции желательности (по
Харрингтону [9, с. 26]);
3.2) построение зависимости Y
3
от X
1
и X
2
, то есть Y
3
= f
3
(X
1
, X
2
);
3.3) нахождение координат X
1m
, X
2m
глобального максимума функции f(X
1
, X
2
) на области
действия;
3.4) построение почти стационарной области экстремума
ω
в окрестности точки (X
1
m
, X
2
m
)
методом доверительных интервалов [3, 10; Р3.6.2].
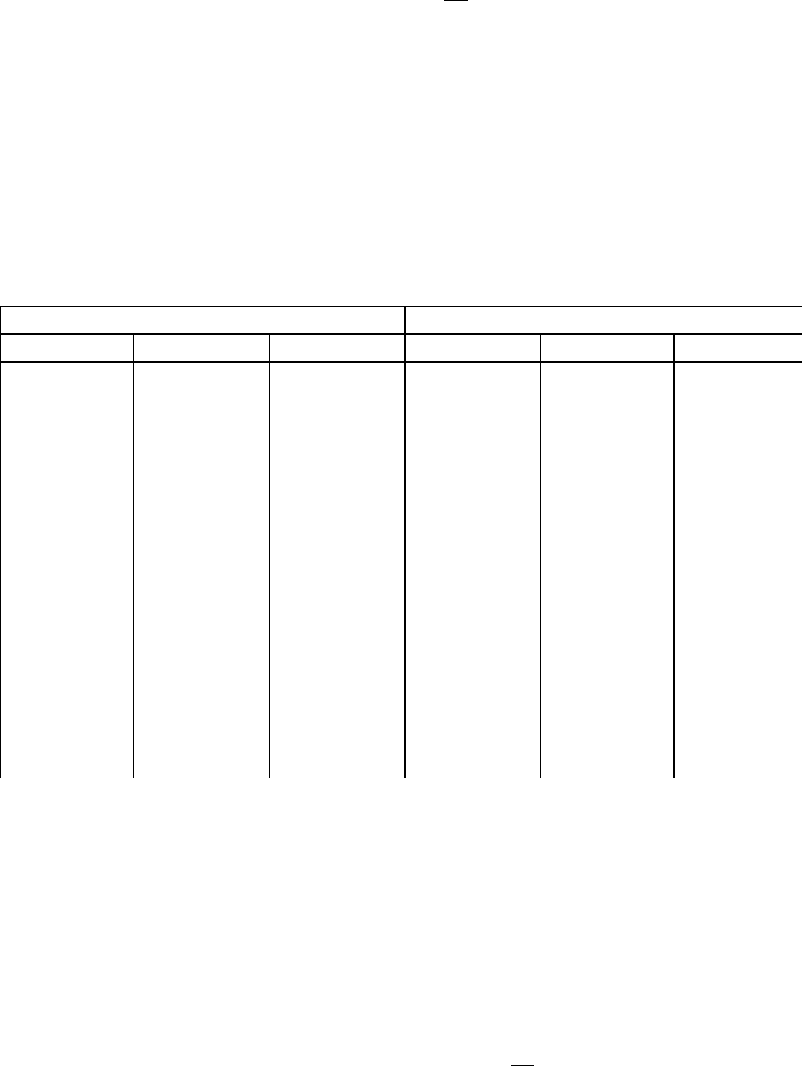
Таблица 1
Результаты исследования механических свойств эпоксидных композиций (ЭК).
Основные компоненты ЭК Отклики
X
1
X
2
X
3
Y
1
, МПа Y
2
, кДж/М
2
Y
3
, %
41,4 0,00 34,5 28,7 2,8 59
41,4 3,30 32,5 34,5 3,1 70
41,4 6,20 30,8 39,5 3,7 79
41,4 8,80 29,2 40,4 4,0 82
41,4 11,2 27,9 33,8 4,0 75
41,4 17,1 24,5 28,3 3,9 66
41,4 21,7 21,7 27,5 2,8 55
22,9 0,00 45,9 29,3 2,7 58
19,2 15,4 38,5 17,2 2,1 18
17,3 24,2 34,5 23,9 2,8 48
15,6 31,2 31,3 13,8 2,2 20
33,3 10,0 33,3 22,4 2,9 46
37,5 9,40 31,3 28,2 3,2 61
45,9 8,10 27,0 27,2 2,5 52
36,4 12,1 30,3 33,2 3,2 69
33,3 19,4 27,8 26,5 2,2 48
30,8 25,6 25,6 16,7 3,0 33
Для построения функции желательности по Харрингтону, согласно методике [9],
экспертами были заданы частные функции желательности d
1
, d
2
для откликов Y
1
и Y
2
соответственно.
Обобщенную функцию желательности Y
3
(см. табл. 1) вычисляли по формуле
(
)
1;0,];1,0[
2121213
21
=+>∈= eeeedddY
i
ee
, (1)
где d
i
- желательность отклика Y
i
,
e
i
- коэффициент «важности» отклика Y
i
; e
1
= 0,6; е
2
= 0,4
(отклик Y
1
немного «важнее» отклика Y
2
).
Желательность вычисляется по значениям безразмерного отклика V
i
d
i
= exp[- ехр(- V
i
)], (2)
связанного, в свою очередь, с откликом Y
i
V
i
= a
i
+ b
i
Y
i
;
{
}
2,1∈i
, (3)
где a
1
= -1,95; a
2
= 9,063
⋅
10
-3
; b
1
= -2,4; b
2
= 1,03 - коэффициенты, найденные методом натянутой
нити [3; Р3.6.3] с помощью прямых, аппроксимирующих зависимость V
i
от Y
i
на графиках.
Значения V
i
на этих графиках вычисляли с помощью формулы (2) по значениям d
i
заданных
желательностей. Значения среднеквадратичного отклонения (CO)
3
Y
S величины Y
3
(табл. 2)
3
вычисляли по формуле [4, с.19]
3
Y
S
= (
2
1
u
+
2
2
u
)
0,5
;
(
)
3
/
iii
uYYs
=∂∂ при
ii
YY
=
;
1,2
i =
; число
степеней свободы
3
Y
f
- по формуле Вэлча [11]
3
Y
f
=
3
4
Y
S
/(
4
1
u
/f
1
+
4
2
u
/f
2
).
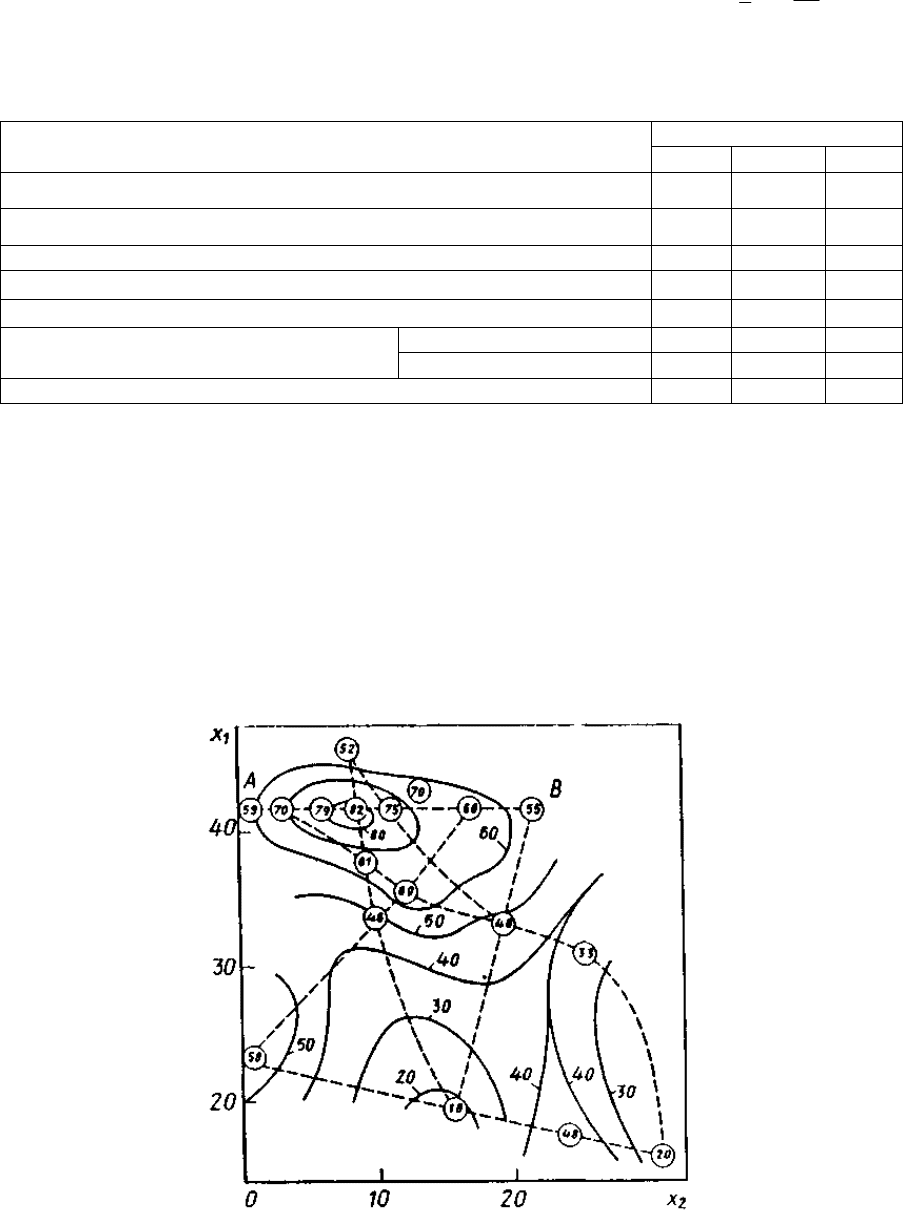
Таблица 2
Предварительные результаты статистической обработки результатов наблюдений.
Отклики
Характеристика
Y
1
Y
2
Y
3
Оценка СО ошибки воспроизводимости
i
Y
s
4,13 0,77 0,086
Число
i
Y
f степеней свободы величины
i
Y
s
57 52 96
Среднее число n
i
параллельных опытов 4,4 4 4
α
-критерий Фишера-Бонферрони однородности дисперсий
0,1 0,2 -
Плечо доверительного интервала
∆
40 0,76 0,083
диабазовая мука X
1
, % 41,4 41,4 41 Координаты максимума отклика
моноэпоксиэфир X
2
, % 8 9,6 8,3
Значение максимума отклика Y
m
41 4,03 0,83
При обобщении данных табл. 1 строили зависимости Y
i
= f
i
(X
1
, X
2
). В построениях с
помощью известного метода контурно-графического анализа [12, с. 42], который обычно
применяется для построения горизонталей на географических картах [13, с. 60], используются
лишь линейные сечения и линейная интерполяция, что снижает точность оценок. Кроме того,
известный метод не предполегает интервальное оценивание поверхности отклика, что приводит к
потере информации об ошибках оценок. Нами предложен метод, лишенный этих недостатков.
Метод статистического контурно-графического анализа.
Описание этого метода будем сопровождать построением линий уровня зависимости
Y
3
= f
3
(X
1
, X
2
) (рис. 1).
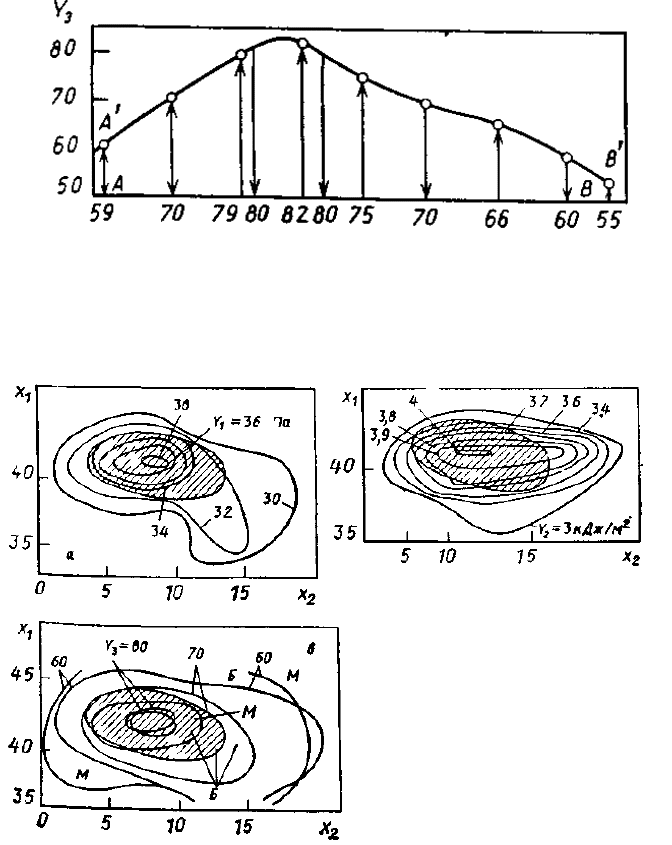
Рис. 1. Построение линий уровня для зависимости обобщенной функции желательности Y
3
от состава эпоксидной композиции:
числа в кружках и на линиях уровня - значения (в %) функции желательности Y
3
в опытах (см. табл. 1)
и после интерполяции соответственно; сплошные линии - линии уровня функции желательности;
пунктирные линии - вспомогательные сечения поверхности отклика.
4
По данным табл. 1 в координатах X
1
- X
2
наносим точки (Х
1i
, Х
2i
). Через эти точки проводим
множество вспомогательных линий сечения или профильных линий [13, с. 104] (см. пунктиры на
рис. 1) от руки, с помощью лекал или сплайна (упругой проволоки или пластины, укрепляемой на
чертеже булавками или грузами). Затем прямоугольный лист плотной миллиметровой бумаги
ставим одним краем на линию сечения, например, на линию AB (рис. 1). Значения откликов Y
3
i
в
точках (Х
1
i
, Х
2
i
), лежащих на линии AB, переносим на миллиметровую бумагу в определенном
масштабе (рис. 2). Через эти точки проводим плавную кривую А'В' - профиль поверхности
отклика. Далее строим несколько горизонтальных прямых через заданные значения отклика (через
точки Y
3
, равные 60, 70 и 80 % на рис. 2), точки пересечения горизонтальных линий с профилем
А'В' проектируем обратно на линию сечения AB (рис. 1). Аналогичным образом проектируем
точки равных значений отклика на остальные линии сечения. Наконец, точки равных значений
отклика соединяем (с помощью лекал, или „от руки“) плавными линиями уровня (рис. 1).
Рис. 2. Профиль А'В' поверхности отклика вдоль профильной линии АВ (рис. 1):
на оси абсцисс приведены табличные значения отклика Y
3
i
, проектируемые на профиль А'В' (стрелки вверх) и
интерполированные значения (стрелки вниз).
Аналогично построены зависимости Y
1
= f
1
(X
1
, X
2
) и Y
2
= f
2
(X
1
, X
2
), рис. 3.
Рис. 3. Зависимость прочностных свойств эпоксидной композиции от ее состава:
а - для разрушающего напряжения при изгибе, Y
1
, МПа; б - для ударной вязкости, Y
2
, кДж/м
2
; в - для
обобщенной функции желательности Y
3
, %; заштрихована почти стационарная область максимума
прочностных свойств (
ω
); линии Б построены быстрым графическим методом; линии M - машинным
аналитическим методом; оконтурена область
ω
, полученная машинным методом.
Поверхность отклика проходит точно через средние значения отклика в точках плана; числа
п
i
опытов в каждой точке почти одинаковы (табл. 2). Поэтому можно считать, что интервальная
оценка поверхности отклика приближенно совпадает с интервальными оценками отклика в точках
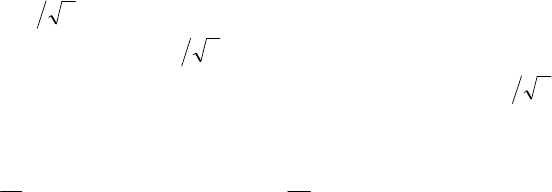
5
плана. Верхняя
B
i
Y
ˆ
и нижняя
H
i
Y
ˆ
границы интервальной оценки поверхности отклика при
необходимости могут быть построены с помощью полученных выше поверхностей Y
i
= f
i
(X
1
, X
2
),
поскольку
B
i
Y
ˆ
= f
i
(X
1
, X
2
) +
∆
i
;
H
i
Y
ˆ
= f
i
(X
1
, X
2
) -
∆
i
, (4)
где
∆
i
- плечо доверительного интервала
2/;
5,0
вос αfiii
tns
−
=∆
, (5)
где t
f;
α
/2
- верхний
α
/2-предел распределения Стьюдента с f степенями свободы [8]; 1 –
α
-
доверительная вероятность.
Примем 1 -
α
= 0,95, тогда
α
/2 = 0,025. По номограмме Бойда [3, 10; рис. 4Р1] находим
значения t
f
; 0,025
и вычисляем значения
∆
i
(см. табл. 2).
Почти стационарную область максимума обобщенной функции желательности можно
построить методом доверительных интервалов [3, 10; Р3.6.2]. Для этого задаемся уровнем
значимости
α
= 0,05. Строим новый доверительный интервал с доверительной вероятностью
0,93 - 2
α
= 0,83 и плечом, равным 2
3
∆ = 0,059. Через точку
H
m
Y
3
ˆ
максимального значения
нижней доверительной границы
(
)
2,
ˆ
32133
∆−= XXfY
H
проводим плоскость
H
m
Y
3
ˆ
= const.
Линия пересечения этой плоскости с верхней доверительной границей
(
)
2,
ˆ
32133
∆+= XXfY
B
и образует границу искомой почти стационарной области
ω
(рис. 3, в).
В качестве «машинного» метода решения поставленной задачи использовали метод
многомерного регрессионного анализа [4]. Первая попытка аналитического обобщения
зависимостей откликов Y
i
(
3,1=i
) от факторов X
j
(
2,1=j
) по данным табл. 1
аппроксимирующими полиномами четвертого порядка не увенчалась успехом: модели оказались
неадекватными данным (дисперсии воспроизводимости откликов
2
вос i
s
и остаточные дисперсии
моделей
2
ост i
s оказались неоднородными). Это объясняется большой сложностью
(многоэкстремальностью) поверхностей отклика и затруднениями, связанными с подбором
адекватных базисных функций модели. Поэтому вместо аппроксимирующих функций
воспользовались интерполирующей функцией. Известно [4, с. 222], что полином высокого
порядка для интерполяции часто не подходит из-за существенных осцилляций в промежутках
между узлами интерполяции. Наиболее гладкой интерполирующей функцией может быть сплайн-
функция [4, с. 223]. Воспользуемся сплайн-функцией Смоляка [5]
()()()
[]
;,
1
2211213
∑
=
−−+++=
N
i
ii
XXXXHiDCXBXAY
H (U, V) = (U
2
+ V
2
) ln (U
2
+ V
2
) (6)
Коэффициенты A, В, С, D(i) формулы (6) определяли по данным N = 17-ти опытов (табл. 1) с
учетом трех дополнительных условий
()()()
∑∑∑
===
===
N
i
N
i
i
N
i
i
XiDXiDiD
11
2
1
1
0 ;0 ;0
по
специальной программе на ЭВМ ЕС-1022. В программе реализован также алгоритм построения
линий уровня (Y
3
= const) функции (6).
Построенные таким образом «машинные» линии уровня (M на рис. 3, в) хорошо совпадают с
линиями уровня Б, построенными быстрым контурно-графическим методом. Глобальному
максимуму функции (6) Y
3
m
= 0,83 соответствуют координаты X
l
m
= 41,4, Х
2
т
= 8,22. Формула (6)
громоздка. Практический интерес представляет не вся поверхность отклика f
3
(X
1
, X
2
), а лишь
окрестность точки глобального максимума. Поэтому по опытам 2 - 5, 13 и 14 (см. табл. 1),
принадлежащим окрестности этой точки (см. рис. 1 и 3, в), получили простую аппроксимацию
22
31212
ˆ
1,130,0880,01360,005622,8
YXXXX=+−−−; (7)
CO остаточной ошибки s
03
= 0,028. Максимуму функции (7) Y
3
m
= 0,89 соответствуют координаты
X
l
m
= 41,4 и Х
2
т
= 7,86.
С помощью аппроксимации (7) можно также построить почти стационарную область
ω
глобального максимума функции
(
)
2133
,
ˆ
ˆ
XXfY =
. Для этого запишем функцию (7) в
канонической форме
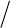
6
Y
3
= 0,89 - 0,0136 (X
1
- X
1m
)
2
- 0,0056 (X
2
- X
2m
)
2
. (8)
Условие адекватности функции (8) результатам наблюдений имеет вид [9, с. 126]
22
03 вос 31;96;0,05
4,
ssF
≤=
(9)
где s
вос3
- СО ошибки воспроизводимости отклика Y
3
(см. табл. 2); F = 4 - верхний пятипроцентный
предел распределения Фишера с числами степеней свободы 1 и 96.
Искомой областью
ω
является геометрическое место координат максимума X
im
(i = 1,2),
варьируемых в выражении (8) и удовлетворяющих условию (9). Граница области
ω
(см. рис. 3в)
является геометрическим местом точек, удовлетворяющих условию (9), в котором знак
неравенства заменен знаком равенства [14].
Таким образом, быстрые графические и машинные аналитические методы
статистической обработки данных с малым числом варьируемых переменных дают
практически одинаковые результаты. Однако графические методы проще и быстрее
приводят к цели.
Наилучшие прочностные свойства - разрушающее напряжение при изгибе 37,9
±
8,6 мПа,
ударную вязкость 3,9 ± 0,4 кДж/м
2
(с доверительной вероятностью 95 %) имеет эпоксидная
композиция следующего состава (%): диабазовой муки - 39
≤
X
1
≤
43; моноэпоксиэфира жирных
кислот таллового масла - 4
≤
X
2
≤
13; эпоксидного олигомера – X
3
= (100 – X
1
- X
2
)/1,7; фталевого
ангидрида - 0,6X
3
; аэросила A-175 - 0,05X
3
; белой сажи, модифицированной моноэтаноламином -
0,05X
3
.
Перспективы. В 21-м веке всюду стали внедряться качественно новые средства
обработки информации – персональные (в том числе и переносные) ЭВМ в сочетании с
возможностью использования программных продуктов из интернета.
Теперь проблема быстрой обработки статистических данных в «полевых» условиях
упирается лишь в финансовые возможности исследователей (пока переносные ЭВМ
сравнительно дороги) и уровень их квалификации (который необходимо непрерывно
совершенствовать).
Литература
1. Ашмарин И. П., Васильев H. H., Амбросов В. А. Быстрые методы статистической обработки и
планирование эксперимента. - Л.: Изд-во ЛГУ, 1975. - 79с.
2. Кенуй M. Г. Быстрые статистические вычисления. Упрощенные методы оценивания и проверки.
Справочник. - M.: Статистика, 1979. - 72с.
3. Цейтлин H. А. Методы статистической обработки результатов наблюдений при пылегазовых замерах.
– Харьков: НИОХИМ, 1981. - 53с.// Рукопись деп. в ОНИИТЭХИМ г. Черкассы 7.8.1981, № 725 ХII-Д81.
4. Себер Дж. Линейный регрессионный анализ. - M.: Мир, 1980. – 456 с.
5. Смоляк С. А. Экономика и математические методы. – 1971. - Вып. 3. - С. 419 - 431.
6. Бейко И. В., Бублик Б. H., Зинько П. H. Методы и алгоритмы решения задач оптимизации. – Киев:
Высшая школа, 1983. - 512с.
7. Прилуцкая H. В. и др. ЛKM. – 1978. - № 1. - С. 30 – 38.
8. Цейтлин H. А. Применение методов математической теории эксперимента в содовой
промышленности. // Обз. инф. Сер. Содовая пром-сть. - M.: НИИТЭХИМ, 1984. - 36 с.
9. Новик Ф. С., Арсов Я. Б. Оптимизация процессов технологии металлов методами планирования
экспериментов. - M.: Машиностроение, 1980. - 304 с.
10. Цейтлин H. А. // В кн.: Методы математической статистики в основной химии. - Труды НИОХИМ. -
Харьков, 1981. - Т. 53. - С. 82 - 89.
11. Цейтлин H. А. // В кн.: Процессы и аппараты производств основной химии. - Труды НИОХИМ. -
Харьков, 1981. - Т. 56. - С. 29 - 38.
12. Саутин С. H.
Планирование эксперимента в химии и химической технологии. - Л.: Химия, 1975. -
48с.
13. Модринский Н. И. Геодезия. - Л.: Гидрометиздат, 1954. - 392 с.

1
4. Гипотезы о ничтожной погрешности
Опыт - это способность совершать ошибки со знанием дела. Александр Михеев
Несмотря на то, что названная задача встречалась на практике часто, её решения в
литературе обнаружить не удалось. Приведём в краткой записи сначала её постановку, схему
решения и некоторые сферы приложения (по материалам обзора [1]), а затем – то же в
подробном изложении с примерами расчётов – в последующих разделах.
Пусть выборочная дисперсия
2
Y
S
с f степенями свободы является оценкой дисперсии
2
Y
σ
случайной величины Y и Y ~
(
)
2
,
Y
N
νσ
. Элементы
j
y
выборки
{
}
1
Im
N
j
i
yY
=
⊂ (
Im
- множество
значений) измерены со случайной погрешностью измерения ε ~
(
)
2
0,
u
N
σ
, с дисперсией
2
u
σ
,
оценка которой
2
u
S
имеет
ϕ
степеней свободы (будем следовать традиции метрологов называть
«ошибки» «погрешностями»). Необходимо проверить гипотезу о том, что дисперсия
2
u
σ
погрешности измерения ничтожно (пренебрежимо) мала по сравнению с дисперсией
2
Y
σ
случайной величины Y.
Очевидно, что пренебречь дисперсией погрешности измерения
2
u
σ
можно в том случае,
если она не превышает среднеквадратичного отклонения (СО)
2
Y
S
σ
выборочной дисперсии
2
Y
S
, являющейся оценкой генеральной дисперсии
2
Y
σ
измеряемой случайной величины Y.
Это позволяет записать одну гипотезу
Н
Т
:
2
2
Y
u
S
σσ
< против другой гипотезы Н
Э
:
2
2
Y
u
S
σσ
> . (1)
Для того чтобы одну из двух гипотез Н
Т
или H
Э
назвать альтернативной H
1
, а другую -
нулевой H
0
, необходимо учитывать, какую из них предпочитает принять лицо, принимающее
решение
(ЛПР). Одну гипотезу, которую предпочитает принять ЛПР, рекомендуется назвать
альтернативной (H
1
), а другую - нулевой (H
0
) [Р1].
В другой постановке (способом «отрицания отрицания» [8, с. 26.]): гипотезу, ошибочное
отклонение которой ведет к большим потерям, ЛПР называет нулевой, а другую - альтернативной.
Например, в нашем случае: одно ЛПР, стремящееся добиться высокой точности
измерений (назовём его ЛПР «точным», или короче – ЛПРТ), не считающееся с затратами
средств на снижение дисперсии погрешности
2
u
σ , может, задав критический уровень значимости
α
kТ
(см. [Т2Р1]), предпочесть гипотезу Н
Т
и считать, что H
1
=
Н
Т
, а H
0
=
H
Э
(см. гипотезу 18 в
[Т3Р1]), то есть
Н
Э
=
2
2
0
:
Y
u
S
H
σσ
≥
против альтернативной гипотезы Н
Т
=
2
2
1
:
Y
u
S
H
σσ
<
. (2)
Другое ЛПР, стремящееся к экономии средств, выделяемых на это мероприятие
(назовём его ЛПР «экономным», или короче – ЛПРЭ), может предпочесть гипотезу H
Э
и, задав
другой критический уровень значимости α
kЭ
(см. [Т2Р1]), считать, что H
1
=
H
Э
, а H
0
= Н
Т
(см.
гипотезу 17 в [Т3Р1]), то есть
Н
Т
=
2
2
0
:
Y
u
S
H
σσ
≤
против альтернативной гипотезы Н
Э
=
2
2
1
:
Y
u
S
H
σσ
>
. (3)
Ту же формулировку получим и при другой постановке гипотез [8]. ЛПРТ полагает, что
причиной наибольших потерь является ошибочное отклонение гипотезы H
Э
, приводящее к
завышенной оценке ДВО
2
y
S , и поэтому определяет, что H
0
=
H
Э
, а H
1
=
Н
Т
, а ЛПРЭ полагает, что
наибольшие потери обусловлены ошибочным отклонением гипотезы Н
Т
, которое приводит к
перерасходу средств на снижение дисперсии
2
u
σ
, и поэтому считает, что H
0
=
Н
Т
, а H
1
=
H
Э
.
Оценка CO дисперсии
2
Y
S
есть
2
Y
S
S
=
()
0,5
2
2
Y
Sf
[9]. Поэтому для проверки нулевых гипотез
Н
0
(2) или (3) можно воспользоваться статистиками Фишера, соответственно (см. [Ф(48)Р1]):
,,
ˆ
f
F
ϕα
=
2
Y
S
S
/
2
u
S
=
()
0,5
22
2
Yu
SfS
(
2
Y
S
S
=
()
0,5
2
2
Y
Sf
); (4)
,,
ˆ
f
F
ϕα
=
2
u
S
/
2
Y
S
S
=
2
u
S
/
2
Y
S
(2/f)
0,5
. (5)
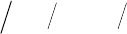
2
Затем, как обычно, ЛПРТ или ЛПРЭ определяют оценки уровней значимости
ˆ
α
Т
или
ˆ
α
Э
(см. [Ф(19), (21)-(27)Р1 или Рис. 2Р1.2.2] для «своих» нулевых гипотез Н
0
(2) или (3)
соответственно; эти гипотезы отклоняют, если окажется, что
ˆ
α
Т
< α
kТ
или
ˆ
α
Э
< α
kЭ
соответственно или не отклоняют в противных случаях.
4.1. Определение ничтожной погрешности прямых измерений [2]
Результаты наблюдений отклика Y на объекте экспериментальных исследований (ОЭИ; см.
[Рис. 1В]) получают с помощью измерительного метода (или устройства) со случайной
погрешностью, обусловленной несовершенством этого метода. Кроме того, наблюдаемые данные
подвергаются «естественному» не устраняемому разбросу, обусловленному природой изучаемого
явления (турбулентными пульсациями [16.11], броуновским движением и т. п. – см., например,
переменную W в формуле [Ф(1)В] и на [Рис. 1В]). Параметры распределения значений
наблюдаемой случайной величины Y могут быть также искажены за счет случайной погрешности
измерительного метода. Повышение точности измерительного метода связано с решением
технических, экономических и статистических проблем. В частности, возникает следующая
статистическая задача определения ничтожной погрешности прямых измерений:
какой должна
быть случайная погрешность измерительного метода, чтобы параметры естественного
разброса случайной величины не были искажены погрешностью этого метода.
В реальной обстановке путем прямого измерения значений Y
i
∈
ImY «чистую» дисперсию
2
Y
σ
СВ Y, свободную от влияния дисперсии
2
u
σ
погрешности измерения СВ Y, оценить
невозможно. Строго говоря, дисперсия
2
Y
σ
СВ Y характеризует разброс значений СВ Y при
параллельных опытах в случае, когда дисперсия
2
u
σ
погрешност
и измерения СВ Y равна нулю. В
реальной обстановке можно оценить лишь сумму этих дисперсий
222
Yuw
σσσ
+=.
В книге [3, с. 45] изложены способы оценки дисперсий
2
u
σ
и
2
w
σ
, называемых,
соответственно, дисперсией ошибки эксперимента по измерению и по воспроизводимости (оценка
22
ww
S
σ
→ имеет ψ степеней свободы). В эксперименте необходимо [2], чтобы вклад дисперсии
2
u
σ
погрешност
и измерения СВ Y в суммарную дисперсию («воспроизводимости»)
2
w
σ
СВ Y был
ничтожно малым. Это требование можно сформулировать в виде гипотезы Н
Т
против Н
Э
(1).
Оценку
2
Y
S
дисперсии
2
Y
σ
можно вычислить по формуле
222
Ywu
SSS
=−
, (6)
а число её степеней свободы - по формуле Вэлча [3]
444
Ywu
fSSS
ψϕ
=−
. (7)
Пример. В предварительных опытах по исследованию зависимости концентрации сульфат-
ионов в очищенном рассоле от различных факторов нашли, что дисперсия погрешности измерения
2
u
S
= 0,033
2
(г/л)
2
с числом степеней свободы
ϕ
= 2, а дисперсия воспроизводимости отклика
(ДВО)
2
w
S
= 0,068
2
(г/л)
2
с числом степеней свободы
ψ
= 7.
Необходимо с позиций ЛПРТ и ЛПРЭ:
1) проверить гипотезу о том, что дисперсия измерения
2
u
σ является ничтожно малой по
сравнению с чистой ДВО
2
Y
σ
;
2) для планируемых экспериментов на ОЭИ оценить верхний допустимый предел дисперсии
2
u
σ погрешности измерения отклика.
Решение. По формуле (6) чистая ДВО
2
Y
S
= 0,068
2
- 0,033
2
= 0,059
2
; по формуле (7)
f
= 0,059
4
/(0,068
4
/7 - 0,033
4
/2) = 5; по формуле (4)
2
Y
S
S
= 0,059
2
(2/5)
0,5
= 0,047
2
.
ЛПРТ предпочитает H
Т
и принимает критический уровень значимости α
kТ
= 0,1.
1) ЛПРТ проверяет гипотезу H
Э
в формулировке (2) против H
Т
. По формуле (4)
5;2;
ˆ
F
α
= 0,047
2
/0,033
2
= 2,0; по формуле [Ф(26)Р1]
α
ˆ
Т
= 1 - (1 + 2/(5٠2))
-5/2
= 0,4 >
k
α
= 0,1.
Следовательно, нулевая гипотеза Н
0
= H
Э
(2) не отклоняется.

3
2) ЛПРТ находит значение величины
k
f,2,
F
α
по той же формуле [Ф(26)Р1] в виде
(
)
{
}
]1-1[ f2
f2
kf,2,
k
−=
−
α
α
F ;
(
)
(
)
(
)
3,911,0152
52
1,0;2;5
=−−=
−
F ; согласно формуле (4) должно быть
2
u
S <
2
Y
S
S
/
k
f,,
F
ϕα
= 0,047
2
/9,3 = 0,015
2
(г/л)
2
.
ЛПРЭ предпочитает H
Э
и принимает критический уровень значимости α
kЭ
= 0,1.
1) ЛПРЭ проверяет гипотезу H
Т
в формулировке (3) против H
Э
. По формуле (5)
2;5;
ˆ
F
α
= 0,033
2
/0,047
2
= 0,5; по формуле [Ф(25)Р1]
α
ˆ
Э
= (2٠0,5/5+1)
-5/2
= 0,6 >
k
α
= 0,1.
Следовательно, нулевая гипотеза Н
0
= H
Т
(3) не отклоняется.
2) ЛПРЭ находит значение величины
k
2;f;
F
α
по той же формуле [Ф(25)Р1]:
(
)
21f
f2
f;;2
k
−=
−
k
F α
α
;
(
)
8,3211,05
52
1,0;5;2
=−=
−
F ; согласно формуле (5) должно быть
2
u
S <
,,
ˆ
k
f
F
ϕα
2
Y
S
S
= 3,8٠0,047
2
= 0,091
2
(г/л)
2
.
ОТВЕТ. ЛПРТ не отклоняет гипотезу о том, что дисперсия измерения
2
u
σ
не является
ничтожно малой по сравнению с чистой ДВО
2
Y
σ
и устанавливает её верхний допустимый предел
2
u
S < 0,015
2
(г/л)
2
на уровне значимости α
k
= 0,1 с
ϕ
= 2 степенями свободы; ЛПРЭ не отклоняет
гипотезу о том, что дисперсия измерения
2
u
σ является ничтожно малой по сравнению с чистой
ДВО
2
Y
σ
и устанавливает её верхний допустимый предел
2
u
S
< 0,091.
Опишем теперь некоторые практические задачи, в которых используются гипотезы (1).
4.2. Определение ничтожной погрешности косвенного измерения [1]
Пусть выполняются измерения величины Y с помощью формулы косвенного измерения
(
)
Yfx
= , где
x
- n-мерный вектор прямо измеряемых величин
(1,)
i
xin
= с некоторыми
случайными погрешностями прямого измерения λ
i
~
(
)
2
0,
i
N
σ
. Дисперсия
2
Y
σ
погрешности
косвенного измерения величины Y обусловлена n дисперсиями
2
i
σ
погрешностей прямого
измерения величин
i
x
. Дисперсию
2
Y
σ
можно представить в виде суммы
2
Y
σ
=
2
u
σ
+
2
V
σ
, которая
состоит из дисперсии
2
u
σ
, обусловленной погрешностью одних факторов в количестве
k (1 ≤ k < n), дающих пренебрежимо ничтожный вклад в дисперсию
2
Y
σ
, и дисперсии
2
V
σ
,
обусловленной погрешностью других (n – k) факторов, дающих существенный вклад в дисперсию
2
Y
σ
. Это утверждение можно сформулировать в виде гипотезы Н
Т
против Н
Э
(1). Установив
ничтожную погрешность измерения (k) величин, можно сосредоточить усилия на уменьшении
погрешности измерения оставшихся n - k величин для существенного уменьшения
погрешности косвенного измерения величины Y.
4.3. Элиминирующий анализ сложных математических моделей [4; Р5]
Пусть имеется адекватная некоторому объекту сложная математическая модель (СММ)
(
)
Yfx
= , где
x
- n-мерный вектор факторов, позволяющая рассчитывать значения отклика Y для
этого объекта. На действующем моделируемом физическом объекте могут быть измерены
значения факторов
, 1,
i
xin
= с некоторыми случайными погрешностями λ
i
~
(
)
2
0,
i
N
σ
. С
помощью СММ по результатам измерений значений факторов вычисляют значения отклика Y с
дисперсией
2
Y
σ
погрешност
и расчета отклика, обусловленной дисперсиями
2
i
σ
погрешностей
измерения факторов
i
x
. Необходимо упростить СММ путем элиминирования (заменой
постоянными значениями) незначимых факторов, чтобы в дальнейшем с помощью упрощенной
СММ рассчитывать значения откликов для данного и однотипных объектов.
Если число факторов n - велико, то, используя СММ при вычислении Y для реального
объекта, нам необходимо выполнять большое число (n) измерений значений случайных величин
