Цейтлин Н.А. Из опыта аналитического статистика
Подождите немного. Документ загружается.


1
3.5. БЫСТРЫЕ ОЦЕНКИ ЦЕНТРА И СТАНДАРТНОГО ОТКЛОНЕНИЯ
Жизнь уходит так быстро, как будто ей с нами не интересно. (Из интернета)
Быстрой однозначной оценкой центра распределения случайной величины является медиана
x
~
. Если число вариант нечетное, медианой x
~
является варианта, делящая ряд пополам. При
чётном числе вариант x
~
- средняя арифметическая двух вариант, ближайших к середине ряда.
Пример 5.
Медианой
x
~
в вариационном ряду, полученном в примере 1 (после исключения
в примере 2 выскакивающей варианты х
8
), является варианта х
4
: x
~
= х
4
= 6, что соответствует
значению 1,06 кг/дм
3
в исходных данных. Быстрая однозначная оценка стандартного отклонения
определяется с помощью размаха
Nx
awS =
'
, (5.1)
где w = x
N
- x
1
- размах варьирования, то есть разность между крайними вариантами в
упорядоченном ряду. Число a
N
, находится по табл. 2 против соответствующего значения N.
Пример 6. По данным примеров 1 и 2 определим размах варьирования: w = x
7
- x
1
= 12 – 1 =
= 11; a
7
= 2,70; тогда
'
x
S = 11/2,70 = 4,1 или с учетом масштаба
'
x
S
исх
= 0,041 кг/дм
3
.
Таблица 2
Значения коэффициента a
N
для оценки стандартного отклонения по размаху, коэффициента k
N
для
расчета границ доверительных интервалов центра по размаху при разных уровнях значимости
α
[3] и коэффициентов c
i
оптимальной линейной оценки стандартного отклонения [12]
N a
N
Значения k
N;α/2
Значения коэффициента c
i
*)
при вариантах x
i
:
α
=0,05
α
=0,01
x
1
x
2
x
3
x
4
x
5
x
6
x
7
x
8
x
9
x
10
2 1,13 -886 886
3 1,69 1,3 3,0 -591 0 591
4 2,06 0,72 1,32 -454 -110 110 454
5 2,33 0,51 0,84 -372 -135 0 135 372
6 2,54 0,40 0,63 -318 -139 -43 43 139 318
7 2,70 0,33 0,51 -278 -135 -62 0 62 135 278
8 2,85 0,29 0,43 -248 -129 -71 -23 23 71 129 248
9 2,97 0,25 0,37 -224 -123 -75 -36 0 36 75 123 224
10 3,08 0,23 0,33 -204 -117 -76 -44 -14 14 44 76 117 …
11 3,17 0,21 0,30 -188 -112 -76 -48 -23 0 23 48 76 …
12 3,26 0,19 0,28 -175 -106 -75 -51 -29 -10 10 29 51 …
13 3,37 0,18 0,26 -163 -101 -74 -52 -34 -16 0 16 34 …
14 3,41 0,17 0,24 -153 -97 -72 -53 -36 -21 -7 7 21 …
15 3,47 0,16 0,22 -144 -93 -70 -53 -38 -25 -12 0 12 …
16 3,53 0,15 0,21 -137 -89 -68 -52 -39 -27 -16 -5 5 …
17 3,59 0,14 0,20 -130 -85 -66 -52 -40 -29 -19 -9 0 …
18 3,64 0,14 0,19 -124 -82 -65 -51 -40 -30 -21 -13 -4 …
19 3,70 0,13 0,18 -118 -79 -63 -51 -40 -31 -23 -15 -7 …
20 3,74 0,13 0,17 -113 -77 -61 -50 -40 -32 -24 -17 -10 -3
*
)
Значения коэффициентов c
i
симметричны относительно медианы, поэтому правая часть таблицы
(многоточие) легко достраивается.
Более эффективной, но менее быстрой является оптимальная линейная оценка СО [10]:
()
1122
1
0,0010,001...
N
x
л iiNN
i
Scxcxcxcx
=
==+++
∑
, (5.2)
где c
i
- коэффициенты (см. табл. 2), значения которых симметричны относительно медианы.
При вычислениях по формуле (5.2) удобно привести подобные члены. Например, при N = 6 получим
(
)
(
)
(
)
116225334
0,001
xл
Scxxcxxcxx
=−+−+−
.
Пример 7. По данным примеров 1 и 2 найти оптимальную линейную оценку СО распределения
плотности.
2
Решение.
По формуле (5.2) S
xл
= 0,001⋅[-278(1 - 12) - 135⋅(4 - 9) - 62⋅(4 - 8)] = 4 или с учетом
масштаба S
xлисх
= 0,04 кг/дм
3
. Быструю интервальную оценку центра распределения (
xвxн
ν
ν
ˆ
,
ˆ
)
определяем по формуле (4.6), где
δ
= w k
N;α/2
, или, короче,
δ
= w k
N
. (5.3)
Число k
N
(точнее, верхний
α
/2 - предел k
N;α/2
) находим по табл. 2 в зависимости от N и
заданного [Т2Р1] уровня значимости
α
.
Пример 8. По данным примеров 1 - 3 и 6 вычислим быструю интервальную оценку центра
распределения: N = 7;
α
= 0,05; k
7;0,025
= 0,33;
δ
= 0,036;
xн
ν
ˆ
= 1,063 - 0,036 = 1,027;
xв
ν
ˆ
= 1,100.
Ответ. Быстрая интервальная оценка центра распределения результатов измерения плотности
равна (1,027; 1,100) кг/дм
3
с доверительной вероятностью 95%.
Из последних примеров видно, что чем «быстрее» метод оценивания, тем шире интервальные
оценки, то есть тем больше «перестраховка» погрешности результата.
3.6. РЕГРЕССИОННЫЙ АНАЛИЗ
Если окажется, что наша логика неверна, все науки станут поэзией. (Станислав Ежи Лец)
Важным этапом экспериментальной работы является исследование зависимостей между
величинами. Исследуют, например, как зависит КПД вихревого пылеуловителя от угла установки
лопаток завихрителя [7; П2Р1.2.1] или как зависит коэффициент сопротивления аппарата от скорости
газа [14] и т. п.
Из-за существенного разброса данных, связанного с ошибками измерительных приборов или с
турбулизацией потоков, искомые зависимости могут проявляться слабо. Методы математической
статистики позволяют обобщать экспериментальные данные о зависимости между величинами и
проверять гипотезы о значимости этой зависимости.
3.6.1. Понятие о регрессии
Если человек говорит правильные слова, это вовсе не значит, что он их понимает.
(Авессалом Подводный)
Пусть некоторая случайная величина Y распределена нормально с центром
ν
y
и стандартным
отклонением
σ
y
, то есть
Y ~ N(
ν
y
,
σ
y
). (6.1)
Пусть существует некоторый фактор X - независимая переменная, которая может принимать
определенные значения X = x. Пусть хотя бы один из параметров распределения (6.1), например,
центр
ν
y
, является функцией x, то есть
ν
y
=
η
(x). (6.2)
Тогда говорят, что имеет место регрессия Y по X, или Y на X. В этом случае зависимую
переменную Y называют откликом, а функцию (6.2) - функцией регрессии. Значение
ν
y
= M{Y|X}
является условным математическим ожиданием, то есть математическим ожиданием Y при условии
(знак |), что X примет значение x.
Слово «регрессия» в переводе с латинского означает «движение назад», что не соответствует
его определению в статистике. Э. А. Боярский [10] предлагал называть регрессию «прогрессией».
Однако этот термин ненамного удачнее, так как , во-первых, он уже используется в математике, а во-
вторых, переводится с латинского как «движение вперед», что также не соответствует его
статистическому определению. Удобнее всего было бы назвать регрессию «гальтоникой» по имени
Ф. Гальтона, который впервые ввел это понятие (по Ф. Гальтону [1] дети обнаруживают «регрессию»
в отношении индивидуальных особенностей родителей, то есть в наследовании индивидуальных
свойств родителей дети как бы возвращаются назад к ним и это движение осуществляется
статистически). Однако в статистической литературе термин «регрессия» потерял первоначальный
смысл (как, например, в физике - термин «атом»).
Анализом в статистике называют проверку различных статистических гипотез. В частности, с
помощью регрессионного анализа проверяют, например, гипотезу о том, что выражение (6.2)
является константой и, следовательно, регрессия Y по X отсутствует (параметр
ν
y
распределения Y не

3
зависит от значений X). Альтернативной (противоположной) является в этом случае гипотеза о
зависимости параметра
ν
y
от X, то есть, о существовании регрессии Y по X.
Другой задачей регрессионного анализа может быть поиск вида функции регрессии
η
(x). Часто
вид и свойства этой функции неизвестны. В таком случае можно по экспериментальным данным
восстановить на графике наиболее вероятный вид этой функции. Построенная таким образом линия
называется эмпирической линией регрессии (ЭЛР).
Можно затем предположить, что функция
η
(x) аппроксимируется уравнением заданного вида
с точностью до коэффициентов (то есть с неизвестными коэффициентами), по экспериментальным
данным оценить эти коэффициенты и проверить, не противоречат ли опыты выдвинутому
предположению.
3.6.2. Построение эмпирической линии регрессии
При любой последовательности вычислений ошибки начнут выявляться на том конце,
который противостоит началу проверки. (Из интернета)
При экспериментальном изучении регрессии Y на X производят ряд из N наблюдений (замеров)
y
i
отклика Y при соответствующих значениях x
i
фактора X.
Полученная двухмерная выборка имеет вид {y
i
, x
i
}, i =
N,1
. На первых этапах статистической
обработки, когда не известен аналитический вид функции регрессии (6.2), бывает достаточно
графической обработки результатов наблюдений. Обычно она заключается в нанесении
экспериментальных точек на график в координатах Y - X (номера точек ставятся в соответствие со
значениями координаты X: x
1
≤
x
2
≤
…
≤
x
N-1
≤
x
N
) и изображении зависимости
ν
y
от X с помощью
ЭЛР.
ЭЛР проводят быстро от руки [15], с помощью лекал или более эффективными методами
скользящей средней [14] так, чтобы точки (x
i
y
i
) были разбросаны вокруг этой линии случайным
образом. ЭЛР является однозначной оценкой зависимости (6.2)
ν
y
=
η
(x). Затем на графике
необходимо
строить интервальную оценку этой зависимости - ДИ для
истинной функции
регрессии (ИФР). ИФР - это воображаемая ЭЛР, которую можно было бы получить обработкой
выборки бесконечно больного объема. Функция (6.2) как раз и является ИФР.
Суть методов скользящей средней
заключается в фильтрации точек вдоль статистического
ряда. Например, для ряда точек (x
i
y
i
) (i =
1,
N
), стоящих эквидистантно (при x
i+1
- x
i
=
∆
x = const) в
методе простой скользящей средней [5, с. 169] выбирается некоторый параметр фильтра k (пусть
k = 2). Берется некоторая точка ряда (пусть (y
3
x
3
)). Вычисляется среднее значение ряда из точки (y
3
x
3
), k точек слева (y
2
x
2
), (y
1
x
1
) и k точек справа (y
4
x
4
) и (y
5
x
5
): 5/
5
1
3
∑
=
=
i
i
yy . Вместо точки (y
3
x
3
) на
график наносится точка (
3
y x
3
). Таким образом «обходят» все точки ряда. Полученные «скользящие
средние» - точки (
i
y x
i
) - соединяют отрезками прямых линий и получают ЭЛР.
К сожалению, известные ранее
методы скользящей средней
обладали
двумя существенными
недостатками: 1) они были предназначены только для однозначного оценивания ИФР, или, иначе
говоря, только для «сглаживания» ЭЛР; 2) значения параметра фильтра k принимались
исследователем без всякого обоснования (обычно интуитивно).
В связи с этим следует заметить, что многие исследователи, не знакомые с математической
статистикой, совсем не обращаются к вычислениям. Они наносят результаты эксперимента на график
и сглаживают их от руки или с помощью лекал. Как показали психологические исследования [15],
такой способ построения ЭЛР вполне соизмерим по точности с эффективным методом (наименьших
квадратов)! Однако построение одной лишь ЭЛР (от руки или даже «методом скользящей средней»)
без доверительного интервала (особенно при большом разбросе данных!) не позволяет решать
важные задачи, которые непременно возникают при исследовании однофакторной регрессии.
Пример 9.
Перечень некоторых задач однофакторного регрессионного анализа.
1. Зависит ли генеральное среднее значение (математическое ожидание
η
(x)) величины Y от
значения фактора X во всей (или части) исследуемой области определения ЭЛР?
Если первая задача решена положительно, то может возникнуть следующая задача.
2. На каком участке фактора X можно пренебречь зависимостью генерального среднего
значения величины Y от значения фактора X?

4
Большой интерес представляют особые участки фактора X, которые являются окрестностью
точек экстремума, перегиба или излома ЭЛР.
3. На каком отрезке оси X некоторая известная теоретическая функция адекватно описывает
результаты данного эксперимента?
4. На каком отрезке оси X результаты повторного эксперимента (или данные других авторов)
совпадают с результатами рассматриваемого эксперимента?
Результаты решения подобных задач в значительной степени зависят от способа получения
экспериментальных данных, уровня априорной информации, сделанных предположений о законе
распределения случайной величины Y и, наконец, от способа статистической обработки данных.
Ниже приведена методика предварительной статистической обработки выборки {y
i
x
i
},
i =
N,1
большого объема (количество точек N >>1) из двухмерной совокупности. Выборка может
быть результатом эксперимента (например, наблюдений y
i
) при заданных эквидистантных
(равноотстоящих) значениях x
i
или «пассивных» наблюдений. Предполагается, что значения x
i
фактора X измеряются с пренебрежимо малой погрешностью [Р4]; расстояния между соседними
значениями факторов x
i+1
- x
i
(
x
i
≤
x
i+1
) невелики (в том смысле, что рост отклика на величину [d
η
(x
i
)/dx](x
i+1
- x
i
), связанную с
приращением фактора на величину
∆
x
i
= x
i+1
- x
i
, пренебрежимо мал [Р6.2.2] в сравнении с разбросом
значений отклика, обусловленным его СО
σ
y
); каждому значению x
i
величины X соответствует одно
значение y
i
величины Y. Для решения перечисленных выше задач предполагается использовать
следующий наглядный метод.
Метод доверительных интервалов.
Что для одного ошибка, для другого - исходные данные. (Из интернета)
Идея метода [Р1.1.2] заключается в построении на графике по определенному правилу
доверительного интервала для ИФР. Вообще, ИФР может быть любая линия, проведенная в пределах
построенного доверительного интервала. В частности, горизонтальная прямая, целиком лежащая в
пределах доверительного интервала, соответствует участку на оси X, на котором условное
математическое ожидание отклика Y не зависит от X (см. п. 1 и 2 из примера 9). ИФР может быть
также график некоторого теоретического уравнения (см. п. 3 из примера 9). Получив два
доверительных интервала по двум группам данных, например, разных авторов, можно искать на
графике область пересечения этих ДИ, в пределах которой провести одну линию (охватываемую
одновременно двумя доверительными интервалами). На соответствующем этой линии участке оси X
условные математические ожидания из двух распределений - результаты наблюдений разных авторов
- отличаются незначимо (см. п. 4 из примера 9).
Проверка гипотез методом доверительных интервалов
Графические построения при интервальном оценивании в методе доверительных интервалов
(ДИ) несколько отличаются от построений, необходимых для обычной иллюстрации погрешности
оценок ИФР. Сам метод подробно описан выше [Р1.2.1]. В дальнейшем будем использовать нулевую
гипотезу о равенстве центров распределения только двух величин Y
1
и Y
2
. (см. [Ф(6); П2; рис.
(б)Р1.2.1]).
Предложенный в работе [14] эффективный модифицированный метод скользящей средней,
предназначенный для построения ЭЛР и доверительного интервала для ИФР, требует использования
ЭВМ. Однако для понимания этого метода и, в некоторых ситуациях (которые мы называем
«полевые условия»), - для практического использования, полезно ознакомиться с его модификацией -
быстрым методом.
Быстрый метод скользящей средней для построения регрессионной зависимости,
характеризующейся большим разбросом точек
Он вчера прислал по почте два загадочных письма:
в каждой строчке только точки - догадайся, мол, сама... (Из интернета)
5
Алгоритмы быстрого метода скользящей средней рассмотрим на примере.
Пример 10.
Результаты экспериментального исследования зависимости коэффициента
ς
сопротивления сухой решетчатой тарелки от числа Рейнольдса Re для парогазового потока в щелях
тарелки представлены выборкой {Re
i,
ς
i
}; i = 107,1 (рис. 1). Построить эмпирическую линию
регрессии и ДИ для истинной линии регрессии, которые позволят решить задачи 1 - 3,
сформулированные в примере 9.
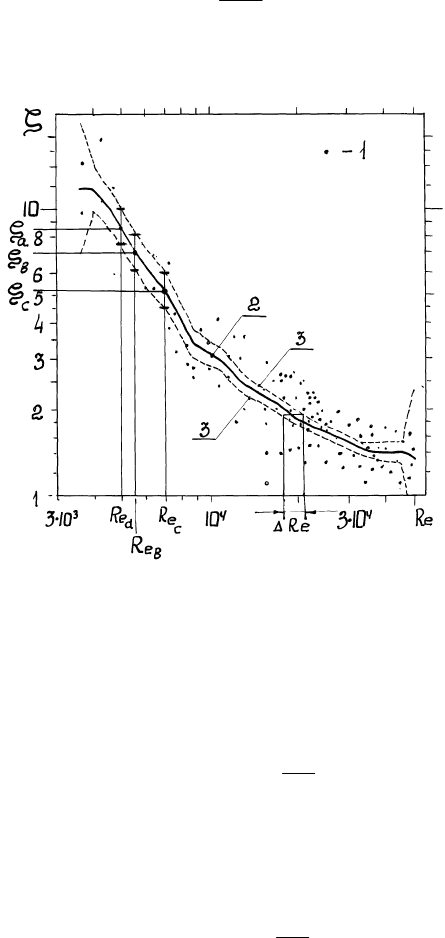
Рис. 1. Зависимость коэффициента сопротивления
ς
сухой решетчатой тарелки от числа
Рейнольдса Re для парогазового потока в щелях тарелки - по данным [14]:
1 - результаты измерений; 2 - ЭЛР, построенная быстрым методом скользящей средней; 3 - границы 82%-
ного доверительного интервала.
На расстоянии, большем, чем
∆
Re (например, Re
c
– Re
d
), регрессия
ς
по Re значима; на расстоянии,
меньшем, чем
∆
Re (например, Re
в
– Re
d
), регрессия
ς
по Re незначима.
Решение. Введем обозначения для нормализующих преобразований [Р2.1] фактора X = lgRe и
отклика Y = lg
ς
. Полагаем, что выборка {x
i,
y
i
}; i = N,1 , где x
i
= lgRe
i
; у
i
= lg
ς
i
; N = 107,
удовлетворяет требованиям однофакторного регрессионного анализа, то есть, значения x
i
измерены с
пренебрежимо малыми погрешностями [Р4], a Y ~ N(
ν
Y
,
σ
Y
). Иными словами, величина Y
распределена нормально с постоянным СО σ
Y
= const и центром ν
Y
, являющимся монотонной
функцией X, ν
Y
=
η
(x).
Для решения примера 10 необходимо выполнить следующие действия [14]:
1) разделить все множество точек {x
i,
y
i
}; i =
N,1
на несколько пересекающихся групп
(пересекающихся подмножеств точек), в каждой из которых зависимость Y от X (точнее, регрессия Y
по X) была бы незначима;
2) найти значения оценок центра распределения отклика (например, средние значения) в
каждой группе;
3) построить доверительные интервалы для центров распределения отклика в каждой группе;
4) соединить отрезками прямых оценки центров отклика в группах - получится ЭЛР; соединить
отрезками прямых соответственно верхние и нижние границы ДИ - получится ДИ для ИФР (точнее -
для условного математического ожидания отклика [14]).
Перечисленные действия лежат в основе численного алгоритма, реализованного в программе
«Модифицированный метод скользящей средней» (ММСС) для ЭВМ [14]. В программе число точек,
собирающихся в группы усреднения, непрерывно меняется. Сначала рассматривается группа из
первых трёх точек; если гипотеза о незначимости регрессии Y по X не отклоняется, в группу
принимается четвёртая точка; если гипотеза о незначимости регрессии Y по X не отклоняется в
группу принимается пятая точка и так далее. Если гипотеза о незначимости регрессии Y по X
6
отклоняется, из группы исключается первая точка, если гипотеза о незначимости регрессии Y по X не
отклоняется, в группу принимается шестая точка и так далее. Для проверки гипотезы о незначимости
регрессии Y по X используются сразу три критерия значимости: критерий Аббе, критерий значимости
парного коэффициента корреляции и критерий Фишера для значимости квадратичной регрессии Y по
X.
Воспользуемся способностью человека (см., например, [18, с. 109]) без помощи вычислений
научиться распознавать группы точек, характеризующих отсутствие корреляции Y с X и регрессии Y
по X. В качестве обучающих выборок используем результат деления на ЭВМ множества точек (см.
рис. 1) на шесть непересекающихся групп a - f (рис. 2).
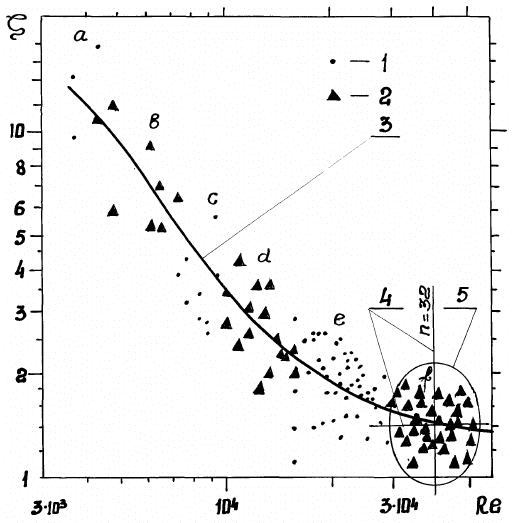
Рис. 2. Вариант деления множества точек (см. рис. 1) на шесть непересекающихся групп a - f, в
каждой из которых регрессия Y = lg
ς
по X = lgRe незначима (выполнено по программе ММСС) [14,
с. 195] на ЭВМ: 1, 2 - результаты измерений; 3 - ЭЛР, проведенная «от руки»; 4 - полуоси эллипса 5,
накрывающего группы из n = 32 точек.
Гипотеза о незначимости регрессии Y по X в каждой группе не отклонялась на уровне α = 0,1 по
трем критериям, упомянутым выше.
Остановимся теперь на каждом действии решения примера 10 подробнее.
1. Для быстрого выделения пересекающихся групп рекомендуется сделать следующее.
Провести от руки первую ЭЛР так, чтобы экспериментальные точки равномерно располагались
по обе стороны от кривой (см. рис. 2 и 3).
7
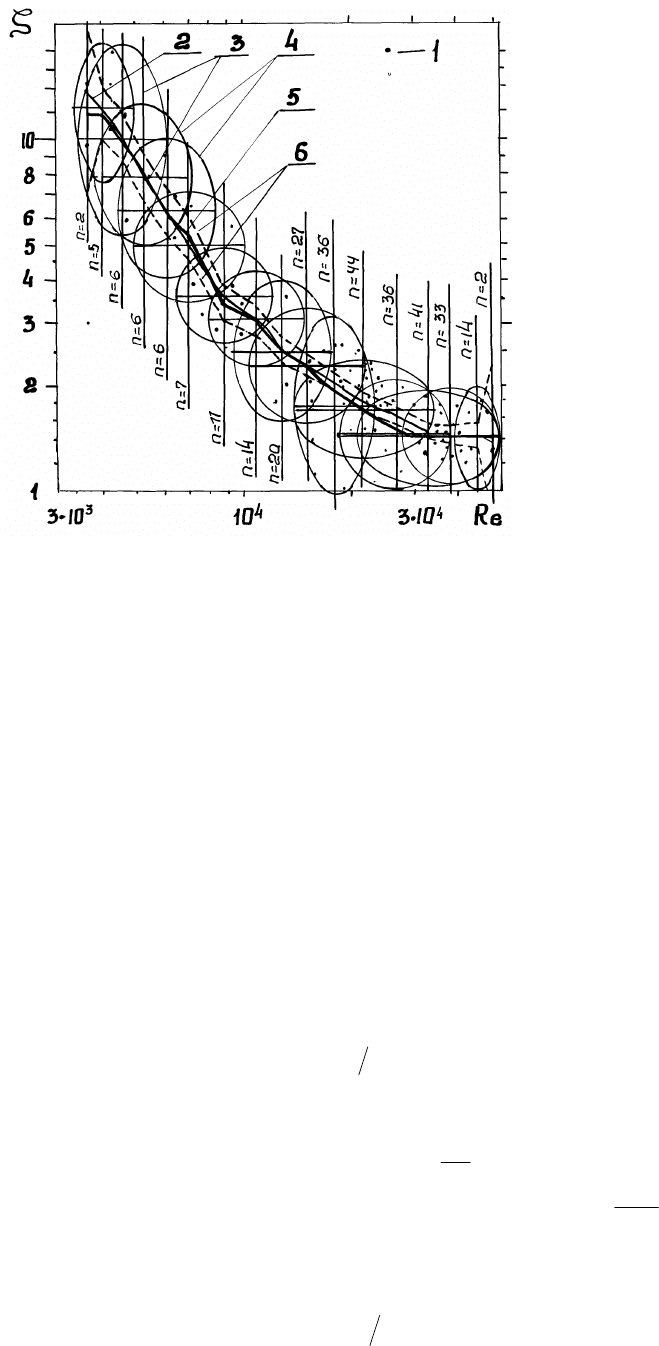
Рис. 3. Быстрый метод скользящей средней (графические построения):
1 - результаты измерений; 2 - первая ЭЛР, проведенная «от руки» (см. рис. 2); 3 - полуоси эллипса; 4 -
эллипсы; 5 - ЭЛР (ломаная линия, проходящая через средние значения точек для пересекающихся
групп, накрытых соответствующими пересекающимися эллипсами; в каждой группе – по n точек).
Провести от руки B (B
≈
N/6) коротких вертикальных прямых через первую ЭЛР
приблизительно на равных расстояниях друг от друга.
Через точки пересечения вертикальных линий с первой ЭЛР провести короткие
горизонтальные прямые.
На основе полученных B скрещивающихся под прямым углом пар прямых, которые
используются как координатные оси, нарисовать B эллипсов. Причем площадь поверхности каждого
эллипса должна быть приблизительно равномерно (без просветов) заполнена экспериментальными
точками. Количество эллипсов B должно быть настолько велико, чтобы рядом расположенные
эллипсы перекрывали друг друга. Точки, охватываемые такими эллипсами, образуют искомые
пересекающиеся группы. Дополнительно с каждого края совокупности следует выделить две группы,
включающие по две точки (x
1,
y
1
), (x
2,
y
2
) и (x
N-1,
y
N-1
), (x
N,
y
N
).
2. Оценки центров распределений
для каждой группы можно получить эффективным
методом по формуле (4.2), где вместо значений x
i
следует подставлять y
i
(см. рис. 5), или еще быстрее
- путем определения медиан (см. пример 5).
3. Построение доверительных интервалов.
Оценим СО отклика Y одним из двух следующих
быстрых методов. Используем разности пар рядом стоящих точек y
i+1
- y
i
; i = 1, 2, ..., N - 1 [13; Р6.2.2]:
()()
[
]
5,0
1
1
2
1
15,0
∑
−
=
+
−−=
N
i
iiY
NyyS . (6.3)
Для условий (на рис. 1) примера 10: S
Y
= 0,1.
Метод размахов [3] ненамного быстрее предыдущего метода (6.3). Определим размах значений
отклика Y в каждой j-й группе
{
}
{
}
maxmin;1,
Yjjiji
i
i
wyyjB
=−=, (6.4)
где
i
max ,
i
min - операторы поиска максимального и минимального i-го значения y
ji
,
jj
ni ,1= в j-й
группе. По формуле (5.1) находим оценки
Yj
S
′
. Затем вычисляем средневзвешенную оценку СО
отклика
Y
S
′
≅
(
)
[
]
5,0
1
2
1
∑∑
==
′
j
B
jjYj
B
j
NNS , (6.5)
8
где N
j
- число точек в каждой группе (на рис. 2 и 3 N обозначено буквой n; для пересекающихся
групп
∑
>
=
NN
j
B
j 1
).
Зададим уровень значимости α (в примере 10: α = 0,05; более строгий - α = 0,1; менее строгий -
α = 0,01). С помощью [рис. 4Р1] определим число Стьюдента t
N-1;
α
/2
(в примере 10: N - 1 = 106;
t
0,025;106
= 1,98). По формуле [Ф(12)Р1.2.1] вычислим значение полуразмахов d
j
ДИ для каждой группы.
Полуразмахи d
j
можно получить с помощью размахов w
Yj
(6.4) по формуле
d
j
= k
Nj
⋅w
Yj
⋅2
-0,5
;
Bj ,1=
. (6.6)
Значения коэффициентов k
Nj
в зависимости от N
j
и
α
определяют из табл. 2. Значения d
j
,
полученные по формуле (6.6), будут заметно больше значений d
j
, полученных по формуле
[Ф(12)Р1.2.1]. (Вывод формулы (6.6) аналогичен выводу формулы [Ф(12)Р1.2.1]).
С помощью значений d
j
строим на графике (см. рис. 3) интервальные оценки центров
распределения Y при соответствующих значениях x
j
(j = 1, 2, ..., В).
4. После завершения построения ЭЛР и ДИ рисунок можно перенести на кальку (см. рис. 1).
Интересно отметить следующее. Первая ЭЛР (проведенная от руки) целиком лежит в
пределах доверительного интервала (см. рис. 1). Это подтверждает вывод Тутубалина [15] о хорошем
совпадении глазомерного и формального методов аппроксимации. Однако, суть статистической
обработки однофакторной регрессии - не только в проведении одной лишь ЭЛР, а в построении
ДИ и последующей проверке статистических гипотез! Отметим также, что быстрый метод
скользящей средней дает ДИ (рис. 1), хорошо совпадающий с ДИ, полученным на ЭВМ по программе
ММСС (рис. 4).
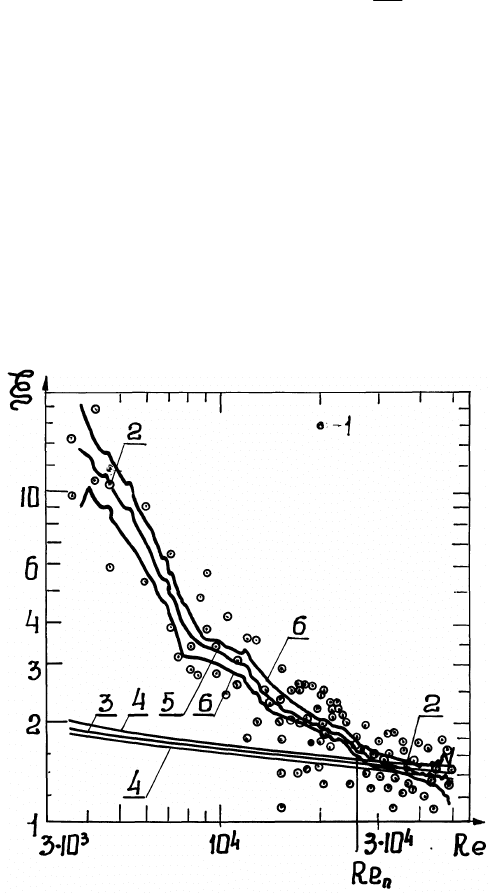
Рис. 4. Проверка гипотезы об адекватности теории опыту методом доверительных интервалов:
1 - результаты наблюдений; 2 - точки начала и конца значимой регрессии; 3 - аналитическая
линия регрессии (построена по полуэмпирическому уравнению [14]); 4 - границы 82%-го
доверительного интервала для истинной (теоретической) линии регрессии; 5 - ЭЛР, построенная по
программе MMCC [14]; 6 - границы 82%-го доверительного интервала для ИФР; при Rе > Re
n
= 25500
«теоретическая» модель адекватна экспериментальным данным.
Замечания.
1. Практика обучения студентов показывает, что учащийся после нескольких упражнений
получает навык столь быстрого построения простых регрессионных кривых и ДИ, что зачастую
отпадает необходимость в дальнейшем обращении к ЭВМ. С другой стороны, при отлаженной
автоматизированной обработке данных альтернативу ЭВМ придумать трудно.
2. На рисунках по возможности надо приводить доверительные интервалы. Популярно говоря,
мы по случайно разбросанным точкам пытаемся воссоздать как бы «доверительный холм»
9
вокруг оцениваемой функции - ИФР. Склоны холма можно изобразить так, как изображают
склоны гор на географической карте, т. е. в виде линий равных уровней значимости, например,
50%, 82% (выделить!), 90%, 95%, 99% и 99,9% или ещё лучше – в аксонометрии (в трёхмерном
пространстве). С компьютером это сделать проще всего.
3. Методы использования ДИ для решения задач оптимизация в условиях неопределённости
обстоятельно описаны в книге [15.39.].
Проверка гипотез (см. задачи 1 - 3 в примере 9).
Однажды Г. Гегелю сделали замечание, что его теория не согласуются с фактами.
- Тем хуже для фактов, ответил учёный.
1. Поскольку во всей области определения ЭЛР х
1
≤
х
≤
x
N
(от минимального x
1
до
максимального x
N
значений фактора X) нельзя провести горизонтальную прямую так, чтобы она не
выходила за границы доверительного интервала (см. рис. 3), то регрессия Y по Х в этой области
значима.
2. При любом значении Х в области х
1
≤ х ≤ x
N
можно выделить участок ∆х (∆Re на рис. 1), в
пределах которого регрессия Y по Х незначима.
3. В литературе [14] имеется полуэмпирическое уравнение, обобщающее эксперименты других
исследователей (см. на рис. 2 график аналитической линии регрессии 3 и ДИ 4). Совмещенные на
одном рис. 2, доверительные интервалы 6 и 4 пересекаются в области Re > Re
п
. Значит, в этой области
полуэмпирическое уравнение адекватно нашим экспериментальным данным.
Содержательный анализ [14] причины неадекватности полуэмпирического уравнения нашим
данным в области Rе < Re
п
позволил прийти к выводу о том, что в щелях тарелок появляется жидкая
пленка, которая образуется в результате частичной конденсации воды из парогазового потока. Это
искажало действительное значение чисел Рейнольдса Re. При высокой скорости парогазовой смеси
(когда Re > Rе
п
) пленка полностью выдувается из щелей!
Значит, кое – в чём великий философ был прав: если теория не согласуются с фактами, - тем
хуже для фактов! :-).
Быстрый метод однозначного и интервального оценивания регрессии, характеризующейся
небольшим разбросом точек
Пусть выборка {x
i,
y
i
}; i =
N,1
характеризуется небольшим разбросом точек; число N мало,
расстояния между соседними значениями факторов x
i+1
- x
i
велики (в том смысле, что значения
приращений [dη(x
i
)/dx](x
i+1
- x
i
) соизмеримы со СО σ
Y
– см. [Р6.2.2]).
Такие зависимости встречаются, например, на диаграммах растворимости. Эти диаграммы
позволяют рассчитывать процессы мокрого улавливания пыли, содержащей кристаллы солей.
Аналитическое описание диаграмм растворимости сложно. Обычно исследователь от руки выполняет
сглаживание экспериментальных точек кусочно-гладкой линией [22]. Другим примером является
график зависимости эффективности осветления сточных вод газоочисток доменных печей от времени
седиментации [24].
В подобных случаях также необходимо кроме ЭЛР, строить ДИ для ИФР.
Пример 11.
Зависимость критерия Y электрохимической коагуляции сильвинитовой суспензии
от относительного количества железа Х, выделенного на аноде, представлена выборкой {x
i,
y
i
};
14,1=i (рис. 5).
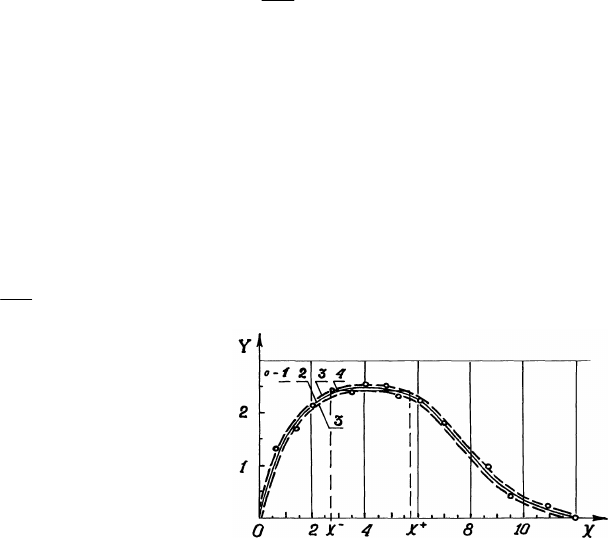
Рис. 5. Зависимость критерия Y электрохимической коагуляции сильвинитовой суспензии от
относительного количества железа X, выделенного на аноде [23]:
10
1 - результаты наблюдений; 2 - эмпирическая линия регрессии Y по Х (проведена исследователями [23]
от руки); 3 - 83%-ный ДИ для ИФР (см. пример 11); х
--
≤
х
≤
х
+
- почти стационарная область максимума
функции регрессии; 4 - вспомогательная горизонтальная прямая.
Построить однозначную и интервальную оценку регрессии Y на X; найти область на оси Х, в
которой значения Y максимальны (см. задачу 2 в примере 9).
Решение. График ЭЛР может быть проведен между точками «от руки» (см. рис. 5).
Оценим среднеквадратичное отклонение отклика по формуле
()
[
]
5,0
2
1
ˆ
NyyS
ii
N
iY
∑
−=
=
, (6.7)
где y
i
- измеренное значение отклика при значении фактора x
i
(i = 1, 2, ..., N);
i
y
ˆ
- значение
отклика на ЭЛР при тех жe значениях x
i
; S
Y
= 0,11.
Зададим уровень значимости α = 0,05 и с помощью [рис. 4Р1] определим число Стьюдента t
f;
α
/2
с числом степеней свободы f = N: t
0,025;14
= 2,1. По формуле [Ф(12)Р1.2.1] при N = 1 найдем
полуразмах d = 0,11⋅2,1⋅2
-0,5
= 0,16. На расстоянии d от ЭЛР наносим нижнюю н верхнюю границу
83%-ного (см. формулу [Ф(14)Р1.2.1]) ДИ (см. рис.5).
Почти стационарная область х
--
≤ х ≤ х
+
максимального значения отклика Y соответствует
проекции на ось Х горизонтальной прямой 4 (см. рис. 5), касающейся нижней границы ДИ и целиком
лежащей в пределах этого интервала.
