Цейтлин Н.А. Из опыта аналитического статистика
Подождите немного. Документ загружается.


4
Наблюдение z
j
, характеризуемое максимальным значением
i
ζ , может быть выбросом
(
)
ZImz
i
∈
.
Если априори считают вероятным появление не более одного выброса, то для его
выявления рекомендуется использовать критерий Смирнова-Груббса [5, с. 3, 18], основанный на
предположении о том, что
{
}
N,1i,,N~z
2
zzii
=σν
. Нулевая гипотеза имеет вид [6]:
N,1i,Const:H
zzi0
==ν=ν
. (9)
Альтернативная гипотеза:
1
:,1,2,,1,1,,;,
zizzjz
HijjN
ννννδ
==−+=+
KK (10)
где
0
≠
δ
- выброс.
Гипотезу Н
0
(9) отклоняют, если
N,j α
ζ>ζ , (11)
где
N,α
ζ
- верхний
α
-предел распределения Смирнова-Груббса [6, с. 324], зависимость
которого от
α
и N для удобства вычисления на ЭВМ аппроксимирована нами [1] формулой
(
)
[
]
{
}
;Et3NlgE4t5,041,1
5,0
2
N,
−++=ζ
α
(12)
;1500N3;001,01,0;246,319569,216266,0E;7857,41672,0t
2
≤≤≥α≥α−α+=α+=
погрешность аппроксимации (12) не превышает 5%. Менее громоздкая аппроксимация [1]
()()()
{
}
,
1,410,00114831,93411,151exp0,2383
N
NN
α
ζα=+−+−−−
(13)
для быстрых расчётов в той же области дает погрешность не более 9%.
Если знак величины δ
ˆ
априори (до опытов) известен, применяют односторонний критерий и
выбирают некий критический уровень значимости
α
k
; если знак δ
ˆ
не известен, применяют
двухсторонний критерий - значение выбранного уровня значимости
α
k
делят на два. Подробнее о
выборе
α
k
см. выше [Р1].
Причиной появления выброса может быть грубая ошибка в измерениях и расчетах; в
данную выборку может быть ошибочно принят результат, являющийся элементом другой
совокупности. Оценки параметров генеральной совокупности должны быть получены по выборке,
в которой влияние выброса на эти оценки как-то нивелировано.
Однако подозрительное наблюдение z
j
может принадлежать генеральной совокупности СВ
Z (z
j
∈
ImZ), а его значительное отклонение от среднего объясняться влиянием тех же случайных
факторов, которые влияют на разброс остальных результатов. Поэтому при исключении
подозреваемого результата z
j
из совокупности, на самом деле принадлежащего ей, может быть
допущена ошибка первого рода (
α
); при включении подозреваемого результата z
j
в совокупность,
на самом деле не принадлежащего ей, может быть допущена ошибка второго рода (
β
).
Ошибочное решение при исключении выброса влечет за собой ошибку в расчете
выборочных моментов распределения СВ Z, затрудняет принятие решения о нормальности
распределения СВ Z.
Используя соответствующий критерий, решение об исключении выброса в статистике
принимают формально [2, 5]. В важных случаях окончательное решение о принадлежности
подозреваемой точки z
j
исследуемой совокупности принимается исследователем совместно с
АСом после содержательного анализа условий эксперимента и всех статистик.
Если эксперимент дорог и исследователь уверен в том, что формально выскакивающая
точка z
j
на самом деле принадлежит множеству Z, то точку z
j
можно и не отбрасывать, а,
например, скорректировать, то есть заменить значением z
j
*, расположенным настолько близко к
среднему значению
z
, насколько это позволяет критическое значение
N,α
ζ критерия выбросов
(11) при заданном
α
=
α
k
. Для этого используют формулы (7) и (11):
kzN,j
;zs*z
α
=
α
+
ζ
=
α
.
(14)

5
Иногда неправильно выбранное нормализующее преобразование (как будет показано ниже
на примерах) может привести к ошибочному отбрасыванию (или ошибочной коррекции)
подозреваемой точки, на самом деле принадлежащей исследуемой совокупности.
Нормализующее преобразование часто выбирают из соображений простоты расчетов.
Удобней всех является тривиальное преобразование z
i
= y
i
. Его можно использовать даже в случае,
когда оно и не соответствует физической природе исследуемой величины (доле, КПД,
концентрации и т. п.). Это допустимо не только при удовлетворении значениям критериев
согласия выборочного распределения с теоретическим, но и когда разброс данных вокруг
среднего значения очень мал, а теоретически допускаемые (с малой вероятностью
α
k
согласно
формуле (11)) точки, далеко отстоящие от среднего значения, не выходят за область физически
допустимых границ.
Проблема выявления выбросов осложнена также возможностью появления более одной
подозреваемой точки, определением важности статистических выводов и стоимостью опытов.
Проблему выбросов можно решать компромиссным и бескомпромиссным методами.
Компромисс
заключается в том, что подозреваемую точку полностью не исключают, а
корректируют, то есть смещают ближе к среднему значению, к пункту, который допустим с малой
«разумной» вероятностью для нормального распределения [см, например, формулу (11)].
Подобная процедура получила название «винсоризации выброса» [7].
Однако и в этом случае не избежать следующего парадокса. Критерий выбросов (например,
Смирнова-Груббса) основан на предположении (подчеркнем это) о нормальном распределении.
Если с помощью этого критерия обнаруживается выброс и он винсоризируется (или
отбрасывается), то оставшиеся данные (особенно при малом объеме выборки), как правило, не
противоречат гипотезе о нормальном распределении (34) или (46). Поэтому процедура проверки
согласия выборочного распределения с нормальным при малой выборке практически заменяется
простой процедурой проверки гипотезы о выскакивающем значении до тех пор, пока
выскакивающее значение не будет исправлено (или отброшено).
Бескомпромиссный метод заключается в том, что распределение исследуемой величины
при наличии выброса признается отличным от нормального и поиск более подходящего
нормализующего преобразования продолжается. Если это не помогает, приходится пользоваться
численными методами обработки данных. Таковым является, например, метод бутстреп, или
метод «размножения выборки»
[8 – 10; Р1.3].
Суть метода бутстреп заключается в том, что в качестве «теоретического» берут не
нормальное распределение, а непосредственно наблюдаемое в эксперименте эмпирическое
распределение СВ, построенное по всем N наблюдённым значениям
(
)
1,
i
yiN
= . Имитируя
численным методом Монте-Карло возможные выборки объемом N элементов из этого, так
сказать, «теоретического» распределения, вычисляют значение оценок его параметров
(математического ожидания, медианы, СО и др.), строят функции распределения этих оценок, с их
помощью определяют интервальные оценки и проверяют статистические гипотезы.
2.1.3. Проверка независимости генерального среднего от порядкового номера наблюдения
Параметры распределения СВ Z оцениваются верно, если генеральное среднее
{
}
z
MZ
ν
=
не зависит от порядкового номера наблюдения. Такая зависимость может возникнуть, если,
например, результаты z
i
получены последовательно во времени, а параметр
z
ν
является функцией
времени. В этом случае дисперсия
2
z
σ
может быть на самом деле малой величиной, но ее оценка
2
z
s
(8), полученная по всей совокупности
{
}
i
z
, будет смещена (в большую сторону) из-за
колебаний
z
ν
во времени. Когда возникают подозрения, что такие колебания имеют место и если
можно предположить, что за период времени между парой последовательно выполняемых
замеров z
i
и
(
)
1
1,1
i
ziN
+
=−
величина
z
ν
практически не изменяется, то в качестве оценки
2
z
σ
хорошо использовать статистику

6
()()
1
2
2
1
1
21
N
zii
i
szzN
−
+
=
=−−
∑
%
. (15)
В общем случае нулевая гипотеза Н
0
о постоянстве генерального среднего имеет вид [6, с. 95]
{
}
{
}
N,1i,ConstzMzM:H
i0
===
(16)
против альтернативы
{
}
{
}
1N,1i,zMzM:H
i1i1
−=≠
+
.
(17)
Для проверки нулевой гипотезы Н
0
против альтернативы Н
1
используется статистика Аббе
2
z
2
z
ss
~
q
ˆ
=
. (18)
Гипотезу Н
0
отклоняют, если
N,
qq
ˆ
α
<
, (19)
где
N,
q
α
- верхний
α
-предел распределения Аббе [6, с. 329] (табл. 1).
Таблица 1
Значения верхних
α
-пределов распределения Аббе,
N,
q
α
в зависимости от объёма выборки
(N) и уровня значимости (
α
) [6]
N
α = 0,001
α = 0,01 α = 0,05
N
α = 0,001
α = 0,01
α
= 0,05
4 0,29 0,31 0,39 32 0,49 0,60 0,71
5 20 26 41 33 50 61 72
6 18 28 44 34 50 61 72
7 18 30 46 35 51 62 72
8 20 33 49 36 52 62 73
9 0,22 0,35 0,51 37 0,52 0,63 0,73
10
24 37 53 38 53 63 73
11
25 39 54 39 53 64 74
12
27 41 56 40 54 64 74
13
29 43 57 41 54 65 74
14
0,31 0,44 0,59 42 0,55 0,65 0,75
15
32 46 60 43 55 65 75
16
34 47 61 44 56 66 75
17
35 48 62 45 56 66 76
18
36 49 63 46 57 66 76
19
0,38 0,51 0,64 47 0,57 0,67 0,76
20
39 52 64 48 57 67 76
21
40 53 65 49 58 67 76
22
41 53 66 50 58 68 77
23
42 54 67 51 58 68 77
24
0,43 0,53 0,67 52 0,59 0,68 0,77
25
44 50 68 53 59 68 77
26
45 57 68 54 59 69 77
27
45 57 69 55 60 69 78
28
46 58 69 56 60 69 78

7
29
0,47 0,59 0,70 57 0,60 0,69 0,78
30
48 59 70 58 61 70 78
31
48 60 71 59 61 70 78
60 61 70 79
В случае необходимости значение
N,
q
α
можно вычислять на ЭВМ по формуле [6, с. 96]
(
)
(
)
∆
′
+−−−=
αα
5,0
2
5,0
N,
1N2Nz1q , (20)
где z
α
- верхний
α
-предел нормированного нормального распределения [6, с. 178];
∆
′
-
поправка; значение z
α
вычисляют по формуле (5), куда вместо z
1
и у подставляют z
α
и
α
k
соответственно; если N > 60, то 0
=
∆
′
; в области 4N
≥
нами подобрана аппроксимация [1]
16,86370,8506680,39629210,85020,6276836,21927
/1.
1322,022155684114,0716
NN
ααα
ααα
−−−
′
∆=〈+⋅〉〈+⋅〉
+++
(21)
В области 0,05 >
α
> 0,001 погрешность формулы (21) не превышает 0,7%.
Если согласно критерию (19) гипотеза (16) отклоняется, следует включить порядковый
номер наблюдения, или связанное с ним время наблюдения в рассмотрение как независимую
переменную и искать вид зависимости (регрессию) математического ожидания
{
}
zM от
независимой переменной, то есть решать задачу анализа временных рядов [11].
Замечание. Аппроксимации (12), (13) и (21) получены нами давно и были приспособлены
для «традиционного» метода проверки гипотез [2, 6, 7]. При использовании «
α
-метода проверки
гипотез» [1] нам необходимо было бы получить подобные аппроксимации, явно выраженные
относительно
α
. Однако приведенные формулы можно использовать и в
α
-методе. Для этого
формулу (12) надо выразить относительно
α
в явном виде
()
()
0,5
222
2
,
1250,16720,16266lg3/62,492
4,78572,9569;1,41
N
EKKNEK
EKKK
ζ
α
α
ζ
=〈−+−−〉
=+=−
,
(22)
а формулу (13) так:
(
)
(
)
(
)
,
1,410,0011483/11,151exp0,23830,17345.
N
NN
ζα
αζ
=〈+−−〉〈−−〉+
(23)
Формулу (20) можно решить относительно
α
численным методом, если представить ее в виде
(
)
(
)
(
)
5,0
5,0
2
N,
2N1Nq1z −−∆
′
+−=
αα
, (24)
а значение
α
вычислять по формулам (21) и (6) методом простых итераций (в формуле (6) надо y и
z
1
заменить на
α
и z
α
соответственно).
2.1.4. Проверка согласия эмпирического распределения с нормальным
При малом объеме выборки (
50N25
≤
≤
) для проверки согласия эмпирического
распределения с нормальным (3) рекомендуется использовать
метод моментов
[6].
Известно, что в качестве мер асимметрии и эксцесса СВ можно использовать коэффициент
асимметрии
a
γ
и нормированное среднее абсолютное отклонение (НСАО)
c
γ
, соответственно.
Если СВ
),(N~z
2
zz
σν
, то эти параметры, соответственно, равны:
0
2
z
)3(
za
=σν=γ ;
(25)
{
}
7979,0)2(zM
5,0
zzzzc
≅π=σν−=σ∆=γ
, (26)
где
)3(
z
ν - третий центральный момент распределения CB Z,
z
∆
- САО СВ Z.
Традиционно нулевую гипотезу о нормальном распределением СВ Z формулируют как
0,5
0
:0(2)
ac
H
γγπ
=∩=
(27)

8
против альтернативы
0,5
1
:0(2).
ac
Hγγπ≠∪≠
(28)
Оценки
a
ˆ
γ
и
c
ˆ
γ
величин
a
γ
и
c
γ
вычисляют по формулам [6]
()
(
)
3
3
(3)3*
1
ˆ
ˆˆ
//;
N
azzi
i
zzNSγνσ
=
==−
∑
(29)
()
*
1
ˆ
ˆˆ
/;
N
czi
i
zzNSγσ
=
=∆=−
∑
(30)
0,5
*2
1
().
N
i
i
SzzN
=
=−
∑
(31)
Гипотезу Н
0
(27) отклоняют, если
,2,,12,,2,
ˆˆˆ
aaNccNccN
ααα
γγγγγγ
−
>∪<∪>
, (32)
где
,,
aPN
γ
и
,,
cPN
γ
- значения верхних Р-пределов распределений оценок
a
ˆ
γ
и
c
ˆ
γ
соответственно
(см., например, таблицы [6, с. 320]). Гипотезу Н
0
(27) не отклоняют, если
,2,,12,,2,
ˆˆ
.
aaNcNccN
ααα
γγγγγ
−
≤∩≤≤
(33)
Применение неравенств (32) и (33) иллюстрирует такие недостатки традиционного метода
проверки гипотез, как потерю информации из-за использования неравенств и неудобства из-за
необходимости использовании уникальных таблиц. Концепция
α
-метода лишена этих
недостатков. Она заключается в следующем [4].
Подлежащая проверке нулевая гипотеза о нормальном распределением СВ Z формулируется
так:
(
)
[
]
{
}
022:H
2
5,0
c
2
a10
=π−γ+γ=θ
(34)
против альтернативы
0:H
11
>
θ
. Для проверки гипотезы Н
0
(34) воспользуемся статистикой
распределения Фишера [6, с. 296] с числами степеней свободы 2 и
∞
:
(
)
22
2,12
2
Fuu
∞
=+
, (35)
где u
1
и u
2
-нормально распределенные случайные величины:
()
0,5
ˆˆ
12
ˆˆ
;2;
aacc
usus
γγ
γγπ
==−
(36)
c
ˆ
a
ˆ
s,s
γγ
- СО, определяемые, в свою очередь, по формулам [6, с. 86]
(
)
NN0796,004507,0s
2
a
ˆ
−=
γ
;
(37)
(
)
[
]
N7N21216s
2
c
ˆ
+−=
γ
. (38)
Подставив эти выражения в формулы (36), а затем - в (35), получим
()()()()
2
2
2,,
ˆˆ
13/1220,7979/(0,090,16)
ac
FNNNNN
α
γγ
∞
=++−+−−
. (39)
Отметим, что по данным авторов [6, с. 234] первое слагаемое правой части равенства (39)
можно записать и так:
(
)
[
]
7N214412N
ˆ
2
a
+−γ . (40)
Далее, согласно
α
-методу проверки гипотез, вычислим оценку
F
ˆ
α
уровня значимости по
простой и точной формуле
[
]
α∞
−
=
α
,,2F
Fexp
ˆ
.
(41)
Условие отклонения гипотезы Н
0
(34), как обычно, имеет вид
0K
ˆ
α
<
α
, где
0K
α
-
критический уровень значимости, заданий исследователем с помощью [Т2Р1] при условии, что
предпочтительна гипотеза Н
0
(34).
Для проверки согласия опытного распределения с теоретическим при большом объеме
выборки (N > 50) достаточно мощным, дающим результаты, не зависящие от способа разбиения
9
выборки на группы (применяемого при использовании хи-квадрат критерия), является
2
ω
-
критерий Мизеса-Крамера-Смирнова [7, с. 260].
Статистика
2
ω
- критерия представляет собой взвешенную сумму квадратов разности
()()()()()()()
{}
2
2
;11,
N
FzFzFzdFzFzFzFzωψψ
∞
−∞
=−=−
∫
(42)
где
ψ
(.) - весовая функция, увеличивающая веса наблюдений на краях распределения.
После интегрирования выражение (42) принимает вид [12]
()
[
]
()
{
}
2
1
ˆ
2(21)ln/21(21)/2ln1
N
ii
i
NiFzNiNFzω
=
=−−−+−−−
∑
, (43)
где
(
)
N,1iz
i
= - результат наблюдения, имеющий новый номер i в предварительно
составленном вариационном ряду
N1ii21
zzzzz
≤
≤
≤
≤
≤
≤
+
KK ; (44)
(
)
i
zF - значение функции теоретического распределения при значении аргумента z
i
.
Если
(
)
i
zF
- функция нормального распределения (3), то для вычисления на ЭВМ
рекомендуется пользоваться аппроксимацией [13, с. 138]
()()
(
)
(
)
(
)
()
()
() ()()
2
11,3302741,8212561,7814780,35656380,3193
815;
110,2316419;0,39894230exp0,5;
;0;01.
z
FMttttt
tM
zzsnpuFF
ζ
ζζ
ζζζζζ
=−−+−+
=+=
=−><⇒−=−
(45)
Нулевая гипотеза о согласии опытного распределения с теоретическим формулируется
непосредственно в виде тождества [7]
(
)
{
}
(
)
zFzFM:H
N0
≡
(46)
против альтернативной гипотезы в виде
(){}()
[]
()
[]
()
0zdFzFzFzFM:H
2
N1
>ψ−
∫
∞
∞−
. (47)
Критические значения
2
ω
- критерия для уровней значимости
{
}
0,3;0,2;0,1;0,05;0,01;0,001;0,0001
α =
принимают, соответственно, значения [6, с. 411]
{
}
1,8;0,6;88,3;5,2;93,1;41,1;12,1
2
=ω
α
, или в виде аппроксимации [1]
(
)
(
)
0,3653
22
ˆ
0,9471exp1,0362;
ωαα
αωω
=
25
0,79;4100,5.
ωα
−
≤≤⋅≤≤
(48)
Гипотеза Н
0
(46) не отклоняется, если, как обычно,
k
ˆ
α
>
α
ω
.
2.1.5. Оценки параметров нормального распределения случайной величины
Несмещенной оценкой генерального среднего
z
ν
величины
),(N~z
2
zz
σν
является
выборочная средняя [14, с. 1]
1
ˆ
N
zi
i
zzN
ν
=
==
∑
.
(49)
Несмещенная оценка генеральной дисперсии
2
z
σ
величины Z при неизвестном
z
ν
вычисляется по формуле (8); несмещенная оценка СО параметра
z
σ
- по уравнению [14, с. 1; 15, с.
230]:
(
)
(
)
ˆ
4344
zzz
ssNNσ
′
==−−
. (50)
(В [Р4] будет показано, что несмещенная оценка
z
s
′
отличается от смещенной
z
s
на
величину, соизмеримую с ошибкой округления и поэтому на практике не используется).

10
СО ошибки выборочной средней определяется по формуле
0,5
zz
ssN
−
=
v
. (51)
2.1.6. Интерпретация результатов статистической обработки данных
Рассмотрим два условия.
Условие 1. Пусть выборка
{
}
YImY
i
∈
является результатом параллельных измерений
отклика Y (например, химического анализа раствора, определения веса образца и т. п.) и разброс
данных Y
i
определяется только погрешностью измерения. Тогда CB Y, как правило,
оказывается распределенной по нормальному закону, то есть
),,y(N~Y
σ
ν
; её МО
ν
интерпретируется как „истинное значение изменяемой величины
“, а СО
σ
является
математической (абстрактной) мерой погрешности измерения.
Если исследователя интересует погрешность измерения, то целью статистической
обработки будет оценка
σ
ˆ
величины
σ
; если его интересует истинное значение изменяемой
величины как результат измерения, то цель - получить оценку
ν
ˆ
величины
ν
; если он
обрабатывает данные впрок, то нужны обе оценки -
σ
ˆ
и
ν
ˆ
.
Условие 2. Пусть выборка
{
}
YImY
i
∈
является результатом измерения некоторого свойства
различных объектов (индивидуумов), или одного ОЭИ (см. Введение), когда фиксированы только
управляемые факторы X
i
, (i = k,1 ), а разброс данных Y
i
, ( N,1i= ) определяется не только
погрешностью измерения отклика, но и влиянием вариации неуправляемых факторов -
регистрируемых X
i
(i = n1,k + ) и нерегистрируемых Z
i
(i = m1, ). Тогда в предположении о том,
что
),,y(N~Y
σ
ν
, МО
ν
интерпретируется как абстрактная точка на числовой оси Y, вокруг
которой наблюдается разброс значений CB Y; абстрактной мерой этого разброса является СО
σ
.
В этом случае параметры
ν
и
σ
распределения СВ Y не имеют физического смысла. Оценки
ˆ
ν
и
ˆ
σ
этих параметров нас интересуют только как способ математического описания функции ее
распределения F(y).
Если нам удастся описать исследуемое распределение СВ Y аналитически – это хорошо,
если нет - не беда! Имея под рукой ЭВМ, будем работать с эмпирическим описанием ФР, то есть-
с эмпирической функцией (ЭФ) плотности вероятности СВ (ЭФПВ СВ) или, ещё лучше - с ЭФ
распределения СВ.
Конечной целью статистической обработки в подобных случаях является сравнение
вероятностных распределений свойств в различных группах однотипных объектов или
распределений отклика Y одного ОЭИ при изменении уровней варьирования фиксируемых
факторов Х
i
.
Если в результате статистической обработки одномерной выборки
{}
1
Im
N
i
i
yY
=
⊂
найдено, что
{}
{
}
2
1
Im~,,
N
izz
i
zZNνσ
=
⊂
где
(
)
,1,
ii
zyiN
ϕ==
, то сверткой информации о
выборке
{
}
i
y
являются выборочные оценки среднего
z
, дисперсии
2
z
s
, объем выборки N и
вид обратной функции нормализующего преобразования
(
)
z
1−
ϕ
.
Эти характеристики дают полное представление о случайной величине Y, позволяют
построить интервальные оценки [14, 15] и проверять различные параметрические гипотезы
[1, 6].
Аппроксимация распределения исходной СВ Y с помощью нормализующего
преобразования является удобным математическим приемом статистического описания
распределения СВ Y. Поэтому оценки параметров нормально распределенной СВ Z - среднее
z
z
ν
→
и СО
zz
s
σ
→
«интерпретируются» лишь как абстрактные коэффициенты в формуле (3).
11
В случае тривиального нормализующего преобразования
ii
yz
=
эти коэффициенты имеют
размерность исходной величины Y и интерпретируются так:
z
- как оценка меры положения
распределения СВ Y, а СО
z
s - как одна из мер ее разброса.
Замечание. Такая популярная в среде математиков мера разброса СВ Z, как дисперсия
2
z
s ,
имеет размерность квадрата исходной величины Z и, как правило, не воспринимается
исследователем. Поэтому везде, где это возможно, вместо дисперсии
2
z
s
лучше использовать СО
z
s
. Например, если исследователю сказать, что дисперсия погрешности измерения температуры
равна 0,25 К
2
, он только разведёт руками. Но если «окажется», что СО погрешности измерения
температуры равно 0,5 К, он скорее всего поймёт, о чём речь.
Большое внимание в статистике, особенно описательной, уделяется использованию средних
величин [15, 16]. В зависимости от вида функции нормализующего преобразования среднего
(
)
1
z
ϕ
−
w
они имеют различные названия (табл. 6).
Таблица 6
Часто используемые средние значения величины Y
Название Функция нормализующего преобразования
Прямая
(
)
i
y
ϕ обратная
(
)
1
z
ϕ
−
Средняя арифметическая
ii
zy
=
z
y
=
Средняя геометрическая
ln
ii
zy
=
или
lg
ii
zy
=
z
ye
=
или
z
10y =
Средняя гармоническая
1
ii
zy
−
=
1
zy
−
=
Средняя квадратическая
2
ii
zy
=
1/2
yz
=
Средняя кубическая
3
ii
zy
=
1/3
yz
=
Обобщением подобных преобразований является среднее по Колмогорову [17]
(
)
(
)
∑
=
−
ϕϕ=
N
1i
i
1
NyY . (52)
Правда, четкого обоснования того, в каком случае какое среднее следует использовать и
почему, нами в статистической литературе не обнаружено. Этот пробел восполнен в настоящем
разделе (см. выше): в каждом конкретном случае следует использовать то среднее, которое
соответствует лучшему описанию исследуемого распределения с помощью нормализующего
преобразования СВ Y. Из всех «средних» только среднее арифметическое интерпретируется как
оценка истинного значения измеряемой величины, когда выполняются прямые (или косвенные)
параллельные изменения (размера, веса, плотности раствора, концентрации компонента в
растворе и т. п.). Именно при многократных измерениях одной и той же величины мы часто
встречаемся со столь малым разбросом результатов, что вполне допустимо использовать
тривиальное нормализующее преобразование и аппроксимировать результаты измерения
нормальным законом распределения.
2.1.7. Применение теоретического закона распределения выборки
Высокий уровень развития ряда прикладных наук нередко позволяет теоретически получить
структуру функции
(
)
,
Fy
θ
распределения случайной величины Y с вектором параметров
θ
.
Например, экспоненциальному закону распределения подчиняется время между моментами
попадания элементарных частиц в счетчик [7, с. 70], распределению Вейбула подчиняется
ожидаемое время отказа в работе механизмов [7, с. 74] и т. п. В этом случае задача обработки
результатов наблюдений сводится к эффективному оцениванию вектора
θ
. Для подобной оценки
используют методы моментов, максимального правдоподобия и др. [7]. Адекватность
12
теоретической функции распределения экспериментальным данным проверяют с помощью
критериев согласия [6, 7, 12].
Пример 3. При исследовании внутренней поверхности стенок карбонизационных колонн
содового производства в конце цикла эксплуатации [3] были выполнены трудоемкие замеры
толщины Y слоя отложений соли бикарбоната натрия на внутренней поверхности 25-ти аппаратов
(мм):
{}{}
25
1
4;4;4;3,6;13;20;2,5;1;2;6;2;10;2;5,6;8;6
;5,1;10;4;4,2;8;8;6,5;9;10.
i
i
y
=
=
Априори было известно, что выбросом может оказаться только максимальное значение
толщины Y. Необходимо оценить параметры распределения толщины Y слоя соли.
Решение. а) Предположим сначала, что, величина Y толщины слоя отложений
подчиняется нормальному закону распределения (нормализующее преобразование
тривиально:
ii
yz
=
). Выявим выброс данных.
Поскольку нулевая гипотеза (9) предпочтительнее альтернативной (10) (у исследователя
есть желание сохранить все результаты), выбираем [Т2Р1] критический уровень значимости
α
k0
=
0,01. Вычисляем статистики 34,6z
=
мм;
2,4s
z
=
мм;
{
}
6j;25,3max
i
N,1i
j
==ζ=ζ
∈
.
Априорная информация о выбросе позволяет воспользоваться односторонним критерием
12,3
25;01,0
=ζ . Поскольку 12,325,3
6
>
=
ζ
, замер №6,
6
y = 20 мм признан выбросом и исключен
из расчетов.
По результатов оставшихся 24-х опытов вычислили опять 77,5z
=
мм;
15,3s
z
=
мм;
⇒
=
ζ
<
=
ζ
10,330,2
24;01,05
замер №5, y
5
= 13 не является выбросом.
Проверим теперь гипотезу (34) о нормальном распределении СВ Z. Будем считать нулевую
гипотезу Н
0
(34) предпочтительней альтернативной Н
1
, так как не отклонение гипотезы Н
0
позволит сразу окончить поиск нормализующего преобразования. Принимаем поэтому (см.
[Т2Р1])
α
k0
= 0,01. Поскольку, согласно расчёту по формулам (39) и (41),
0
ˆ
0,08
Fk
αα
=>
, то
гипотеза Н
0
(34) не отклоняется.
Проверим теперь
адекватность
тривиального нормализующего преобразования
физической природе опытных данных. Согласно формуле (14) при нормальном распределении
величины Y допустимы минимальные значения y
min
= -3,1·3,15 + 5,77 = - 4 мм, лишенные
физического смысла (толщина слоя соли не может быть отрицательной). Расчеты необходимо
повторить.
б) Выберем теперь в качестве нормализующего преобразования функцию
ii
ylgz
=
.
Вычислим статистики
712,0z
=
; 30,0s
z
=
;
⇒
=
ζ
<
=
ζ
12,36,1
25;01,06
оказалось, что замер
y
6
= 20 мм выбросом не является; 01,01,0
ˆ
kF
=
α
>
=
α
; гипотеза Н
0
(34) о нормальном
распределении величины Z не отклоняется.
Можно вычислить также оценку
2
ω
- критерия:
32,0
ˆ
2
=ω
(но только для примера расчётов,
так как воспользоваться ею нельзя из-за малого объема выборки: N < 50).
Далее находим 27,0s
ˆ
2
z
= ; 80,030,027,0q
ˆ
=
=
. Гипотеза Н
0
(16) о независимости
генерального среднего от порядкового номера наблюдений не отклоняется, так как
5,0q80,0q
ˆ
25;01,0
=
>
=
; несмещенная оценка СО 30,0s
z
=
′
.
Ответ. Опыты не противоречат гипотезам о независимости наблюдаемого значения от
номера замера (
{
}
{
}
ConstzMzM:H
i0
=
=
), гипотезе о логарифмически нормальном
(логнормальном) законе распределения толщины Y отложения солей
(
{}
{
}
2
1
Im;~,,
N
izz
i
zZZNνσ
=
⊂ где
(
)
lg,Im,1,25
iii
zyyYi=∈=
); максимальный результат
y
6
= 20 мм не является выбросом; оценки параметров распределения Z: среднее
712,0z
=
и
дисперсия
22
z
30,0s =
; объем выборки N = 25; обратная функция нормализующего
13
преобразования:
k
z
k
10y =
(из этого преобразования следует, в частности, что среднее
геометрическая значение толщины слоя инкрустаций в аппаратах
2,510y
z
==
мм).
Пример 4. По данным примера 3 построить график эмпирической и теоретической функций
распределения толщины Y слоя соли.
Решение. Нумеруем заново элементы преобразованной выборки
{
}
{
}
lg
ii
zy
= в порядке их
возрастания:
N21
zzz
≤
≤
≤
K
. Для построения эмпирической функции распределения
(кумулятивной кривой на рис. 2) найдем накопленную частость:
()()
()
11
0;;
1.
NNN
NN
i
FznpuzzFznpuzzz
N
Fznpuzz
=<=<<
=>
(53)
Теоретическую функцию распределения строим по формуле (3). На оси абсцисс отмечаем
антилогарифмы величины Z, то есть, значения толщины Y слоя, мм (см. рис. 2).
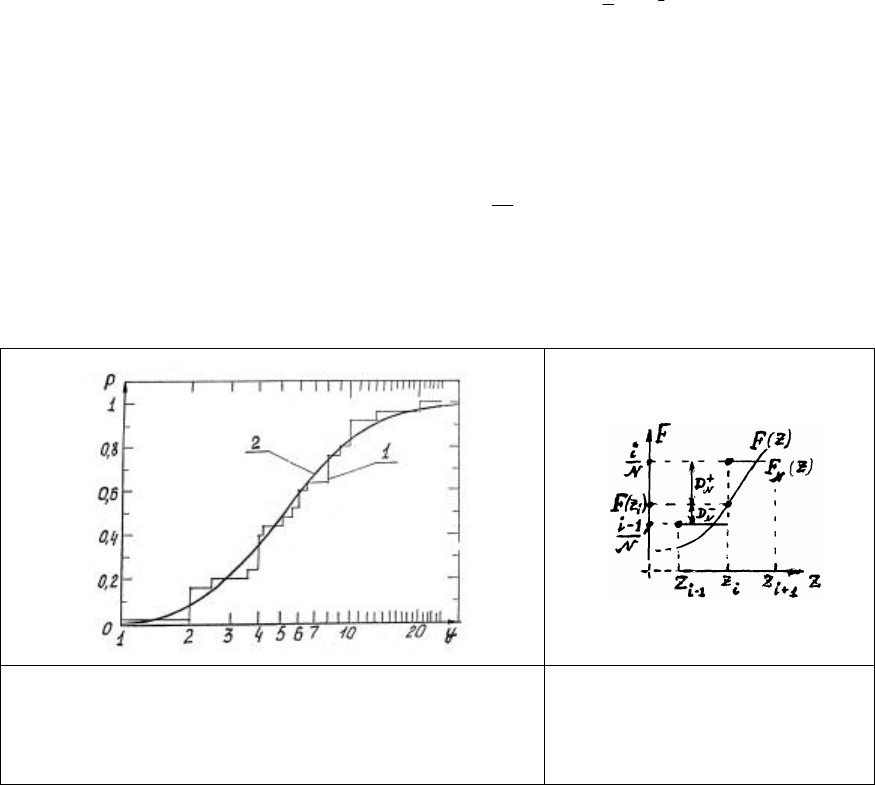
Рис. 2. Эмпирическая (1) и теоретическая (2) функции
распределения толщины слоя отложения солей
(к примерам 3 и 4):
y - толщина отложений (на логарифмической шкале), мм;
Р – вероятность.
Рис. 3. Определение величины
статистик D
+
N
и D
-
N
при
использовании критерия
Колмогорова
2.1.8. Критерий Колмогорова
Нередко исследователь желает убедительно продемонстрировать результаты проверки
гипотез в научном отчёте. Критерий Колмогорова [18, с. 235], несколько менее мощный, чем
критерий
2
ω
, однако более быстрый и способный наглядно демонстрировать результат проверки
гипотезы о согласии выборочного и заданного аналитически непрерывного (в частности,
неизвестного нормального) распределений. Критерий Колмогорова основан на статистике
D
N
=
max
i
|F
N
(z) - F(z)|;
−∞
< z <
∞
, (54)
где F
N
(z) - эмпирическая функция распределения, построенная по данным выборки (2) после её
упорядочения, то есть по вариационному ряду (44). При определении значения статистики D
N
следует учитывать, что эмпирическая функция распределения является ступенчатой (рис. 3).
В точке разрыва z = z
i
функция F
N
(z) скачком переходит от значения (i-1)/N в интервале
z
i-1
≤
z < z
i
к значению i/N, сохраняя последнее в следующем интервале. Наибольшая разность
между F
N
(z) и F(z), то есть значение статистики D
N
= max (D
+
N
, D
-
N
), приходится на одну из таких
точек разрыва. Итак, для определения значения статистики D
N
находят
D
+
N
=
max
i
(i/N - F(z)) и D
-
N
=
max
i
(F(z) - (i-1)/N). (55)
На практике оправдал себя графический способ определения величины D
N
. Из-за его
простоты этому способу чаще всего и отдают предпочтение.
