Цейтлин Н.А. Из опыта аналитического статистика
Подождите немного. Документ загружается.

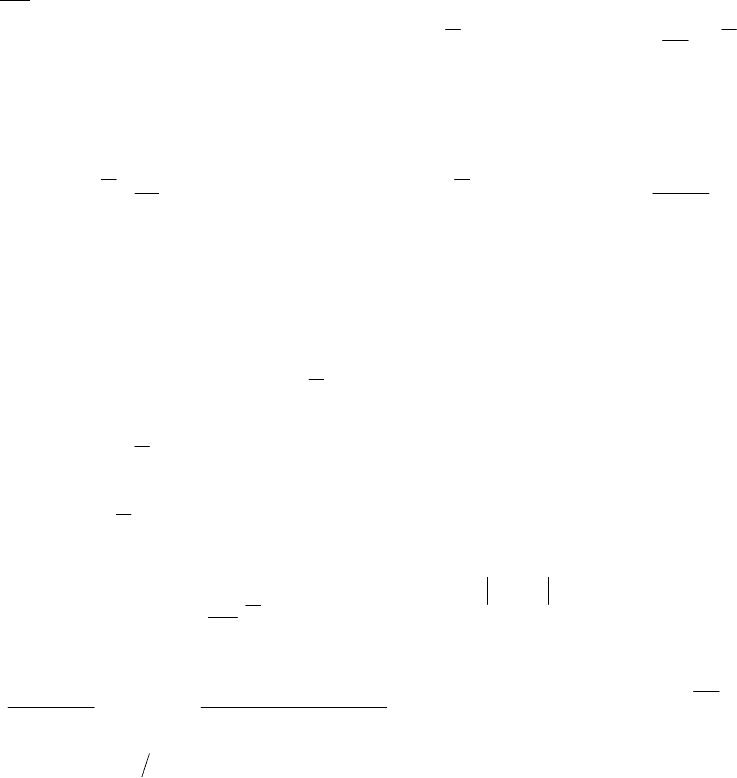
2
менее грубую, чем кусочно-постоянная, аппроксимацию. Удобной в этом случае будет сплайн-
функция.
Аппроксимация сплайн - функцией.
Всякая точная наука основывается на приблизительности. ( Бертран Рассел)
Определим единичные ступенчатые функции аргумента Z ∈ R
'
как:
()
10
1, npu ;
,
0, npu ;
za
Iaz
za
<
=
≥
(2)
()
01
0, npu ;
,
1, npu ;
zb
Ibz
zb
≤
=
>
(3)
()
1, npu ;
,,
0, npu ,
azb
abz
zazb
<<
Π=
≤∪≥
(4)
где a, b – константы.
Назовем сеткой
∆
множество K+1 точек Ψ = {Ψ
0
, Ψ
1
,…,Ψ
к
}, где Ψ
0
< Ψ
1
<…<Ψ
к
, а точки Ψ
i
(Ψ
i
∈ R
'
, i=
k,0
) - узлами. Определим сплайн-функцию Φ
Δ
( z,
β
) с вектором параметров
β
над
сеткой
∆
как функцию аргумента z, совпадающую на каждом интервале (Ψ
i-1
, Ψ
i
] (i= k,1 ) сетки
∆
с некоторым многочленом степени m
i
∈
N.
Сплайн - функции конструируются с помощью ступенчатых единичных функций, или без
них [5-7]. Например, правосторонний сплайн [6, 7] в общем виде
(
)
() ()()
0
1
001
01
,,
i
i
mkm
jj
jii
jijn
ij
zzzIz
Ф
βββ
−
∆
===
=−Ψ+−ΨΨ
∑∑∑
, (5)
где r
i
= max{m
l
}, l
∈
(
i,0
) – степень i - го полинома на интервале (Ψ
i
, Ψ
i+1
), i = (
1,0 −k
), k > 1;
n
i
– число ограничений, накладываемых на сплайн-функцию и её производные в узлах Ψ
i
. При
n
i
= 0 имеются разрывы первого рода непрерывности функции и её производных в точке Ψ
i
при
n
i
> 0 (1 ≤ n
i
≤ m
i
) наблюдаются разрывы первого рода непрерывности n
i
- ой, n
i+1
- ой и т. д. до m
i
-
ой производных функции в точке Ψ
i
.
Частными случаями формулы (5) являются: кусочно-постоянная сплайн-функция
(
)
()
1
011
1
,,
k
ii
i
zIz
Ф
ββ
−
−
∆
=
=Ψ
∑
; (6)
кусочно-линейная
(
)
()()()
1
01001
1
,,
k
iii
i
zzzIz
Ф
ββββ
−
∆
=
=+−Ψ+−ΨΨ
∑
(7)
или кубический сплайн с непрерывной функцией, её первой и второй производными [6]:
(
)
()()()
31
3
0301
01
,,
k
i
iiii
ii
zzzIz
Ф
βββ
−
+
∆
==
=−Ψ+−ΨΨ
∑∑
. (8)
Вместо ступенчатых единичных функций в конструкции сплайна можно использовать
абсолютные величины разностей |z - Ψ
i
|. Например, в кусочно-линейной сплайн-функции [5]:
011
1
(,)
k
ii
i
zzz
W
ββββ
+
∆
=
=++−Ψ
∑
. (9)
Если координаты (Ψ
i
,Y
i
) i = ( k,0 ) узлов этой функции заданы, то коэффициенты β
i
определяются по формулам
(
)
(
)
()
001
11011
2
110
0,5
2; 1,
i
ii
iikik
k
ii
yy
yyin
ββ
+
+++−
=
+
−Ψ−Ψ
=−+−Ψ−Ψ=
Ψ−ΨΨ−Ψ
∑
; (10)
(
)
(
)
∑
=
+
+Ψ−Ψ−=
n
i
i
yy
1
101011
ββ
; (11)
(
)
0
1
10100
Ψ−Ψ−Ψ−=
∑
=
+ i
n
i
i
y βββ
.
(12)
1.3.1 Предварительная обработка данных выборки.
Математик обращается к работнику фото-студии: - Сделайте мне, пожалуйста,
фотографии с этой пленки. - Девять на тринадцать? - Сто семнадцать, а что?!

3
В общем случае исходными данными для построения ЭФРВ являются L пар элементов (x
i
,
g
i
) случайной выборки {(x
i
, g
i
)}, i =
1,
L
из бесконечного множества значений CB X.
Точки x
i
обладают соответствующими весами g
i
, такими что g
i
≥
0. Подготовим эту выборку
для построения ЭФРВ. Для этого составим первый вариационный ряд
{
}
12
,,...,
ijk
n
xxx
, приписав, к
обозначениям x и g, соответственно, нижние индексы так, чтобы
βα
ll
xx ≤
−1
,
(
)
2,
lL
=
. Далее
верхние индексы отбросим.
Для преодоления трудностей при расчете коэффициентов β
i
сплайн - функций необходимо
объединить группы почти совпадающих точек в одно среднее значение. Для этого найдем почти
совпадающие точки x
l
и x
l-1
, такие что x
l
- x
l-1
< ε
x
, где ε
x
– малое число (например, ε
x
= (x
L
- x
1
)·10
-3
);
соответствующие веса точек, попавших в одну группу, сложим. Если в первом вариационном ряду
образовались группы почти совпадающих точек, опять введем новые нижние индексы для
обозначений x и g так, чтобы x
l-1
< x
l
; старые индексы отбросим и получим второй вариационный
ряд {x
i
}={x
1
, x
2
,…, x
N
} из N ≤ L точек.
Введем нормировки c
i
весов точек так, чтобы 1
1
=
∑
=
N
i
i
c . Тогда
∑
=
=
N
j
jii
ggc
1
. (13)
Аппроксимации функции распределения СВ X будут строиться по точкам с координатами
(x
i
, b
i
); i= N,1 , а
∑
=
=
i
j
ji
cb
1
- накопленные суммы нормированных весов (контрольная сумма:
b
N
= 1).
Пример. Получена выборка {(x
i
, c
i
)} = {(7; 3), (1,1; 2), (9; 1), (0,7; 3), (1,2; 1)}, i =
5 ,1
.
Необходимо подготовить её для построения ЭФРВ.
Составим первый вариационный ряд
{
}
,,,,,
3
5
1
4
5
3
2
2
4
1
xxxxx
={0,7; 1,1; 1,2; 7; 9}; зададим малое
число ε
x
= (9 – 0,7)/10 = 0,83. Проверим неравенства x
l
- x
l-1
< 0,83. Получим x
2
– x
1
< 0,83;
x
3
– x
2
< 0,83; x
4
– x
3
> 0,83; x
5
– x
4
> 0,83. Образовалась одна группа почти совпадающих точек,
состоящая из первых трех точек, где x
1
=(0,7 +1,1 + 1,2)/3 = 1. Получим второй вариационный ряд
{x
i
} = {1; 7; 9} с нормированными весами точек c
1
= (2+3+1)/10 = 0,6; c
2
= 0,3; c
3
= 0,1.
Накопленные суммы нормированных весов: b
1
= 0,6; b
2
= 0,9; b
3
= 1.
Итог подготовки: {(x
i
b
i
)} = {(1;0,6), (7; 0,9), (9; 1)}.
1.3.2 Аппроксимация «теоретической» функции распределения.
Определение: «Вход в танк - это отверстие извне вовнутрь,
именуемое в обратном направлении выходом». (Из интернета)
Функцией распределения СВ X является неубывающая функция аргумента,
интерпретируемая как вероятность P события X ≤ x, тo ecть
P = F
т
(x) = Р (X ≤ x). (14)
Область значений этой функции Р
∈
(0,1).
В методе Эфрона [4] функция F
т
(x) используется для расчета значений x
i
с помощью
равномерно распределенных на интервале (0; 1) чисел Р
i
. Поэтому практическое значение имеет
также и
обратная функция распределения (ОФР)
)(
1
PFx
T
−
=
, Р
∈
(0,1). (15)
Замечания.
1. Решая задачу описания прямой и обратной функций распределения, будем учитывать, что
конструируемые аппроксимации используются «временно» – для расчета на ЭВМ интервальных
статистических оценок и проверки гипотез. Конструкции этих функций «временно» хранятся в
памяти ЭВМ и даже не выводятся на печать (желательно выводить их графики).
2. Другой подобной часто решаемой задачей является построение какой-либо несложной
аппроксимации F
е
(x) функции F
т
(x). Для этого можно пользоваться теоретическими функциями
[8], аппроксимациями рядом Эджворта [9], полиномами [10] и упомянутыми сплайнами (2) – (9)
на разреженной М-сетке (см. ниже). Взаимосвязь этих задач определяется конкретным
4
направлением исследования.
Выбор узлов сетки
- Почему в моей комнате на окне две сетки? - спрашивает постоялец горничную. - Та, что
с мелкими ячейками, не пропускает комаров, а та, что с большими, не пропускает мух.
-
Остановимся на задаче построения сплайн - аппроксимации
(
)
1
e
FP
−
ОФР
(
)
1
T
FP
−
СВ Х.
Сейчас в формулах (5) – (12) величины b
i
будут значениями аргументов (Z), a
X
i
- значениями сплайн - функции (Y). Узлы сетки для аппроксимации функции F
T
(Х) могут
задаваться точно так же, как и для
(
)
1
T
FP
−
, только X
i
будут значениями аргумента (Z), a b
i
-
функции (Y).
Значения величин b
i
ограничены интервалом вероятностей (0; 1); величина X может быть
ограниченой интервалом (X
-
, X
+
) или вообще не ограниченной.
Можно предложить по крайней мере четыре типа сеток (назовем их Р-, B- и М - сетками) с
количеством К узлов Ψ
i
, соответственно равным (Р), большим (B) и меньшим (M) количества N
точек (x
i
b
i
) исходного ряда; Р- сетки, в свою очередь, делятся на два типа - не преобразованную
(Р
Н
- сетка) и преобразованную (Р
П
- сетка).
Р
Н
- сетка имеет вид
Ψ
i
= b
i
, Y
i
= X
i
, (i =
1
,N
; k = 1; Рис. 1); (16)
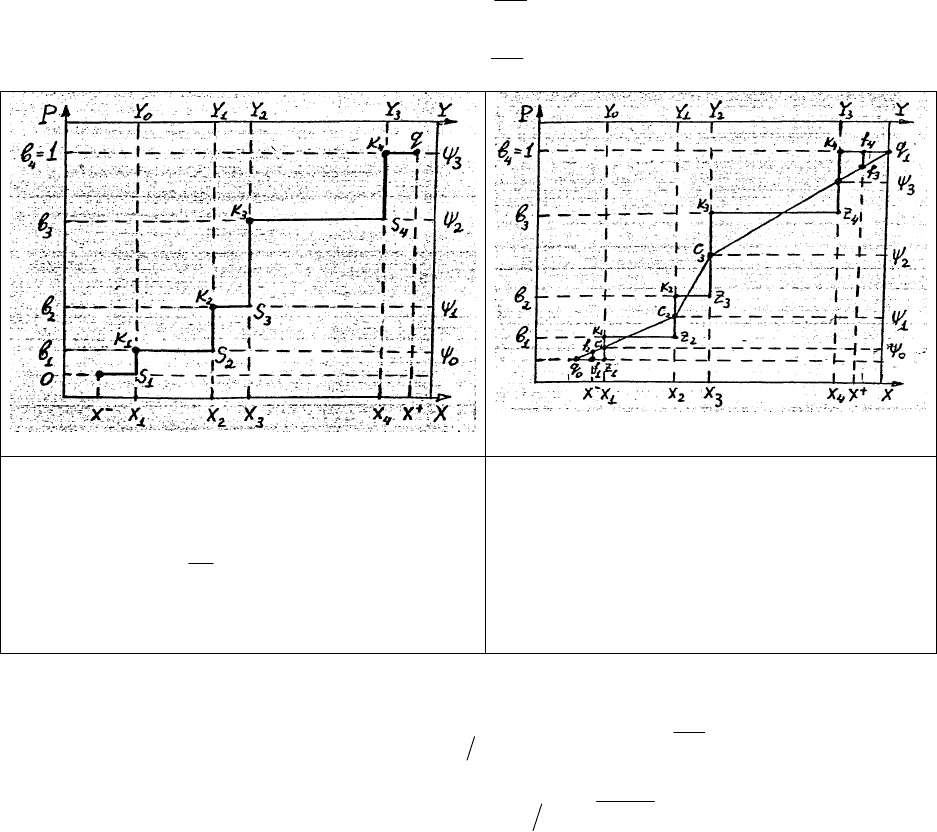
Р
П
– сетка имеет вид
Ψ
i
= b
i
+
i
C
′
/2; Y
i-1
= X
i
, (i =
1
,N
; k = N; Рис. 2); (17)
Рис. 1. Кусочно - постоянные сплайн -
функции (6), построенные на Р- сетке (16):
(X
-
, S
1
], (K
1
, S
2
], (K
2
, S
3
], (K
3
, S
4
]; (K
4
, q) –
функция распределения F
Э
(X), X ∈( X
-1
, X
+
);
(S
i
, K
i
) (i =
14
,
) – обратная функция
распределения
(
)
1
Э
FP
−
.
Рис. 2 Кусочно - линейная сплайн –
функция (9), построенная на Р
П
- сетке (17).
B - сетка имеет вид:
- для индекса j = 0 и четных индексов j = 2i – 2:
(
)
2222
2 =1,
jiiijii
bC;YYXiN
−−
′
Ψ=Ψ=−== ; (18)
- для нечетных индексов j = 2i –1:
()
(
)
21211
+2 =1,1; 22; P
ис. 3
jjijiii
b;YYXXiNkN
−−=
Ψ=Ψ===−=− . (19)
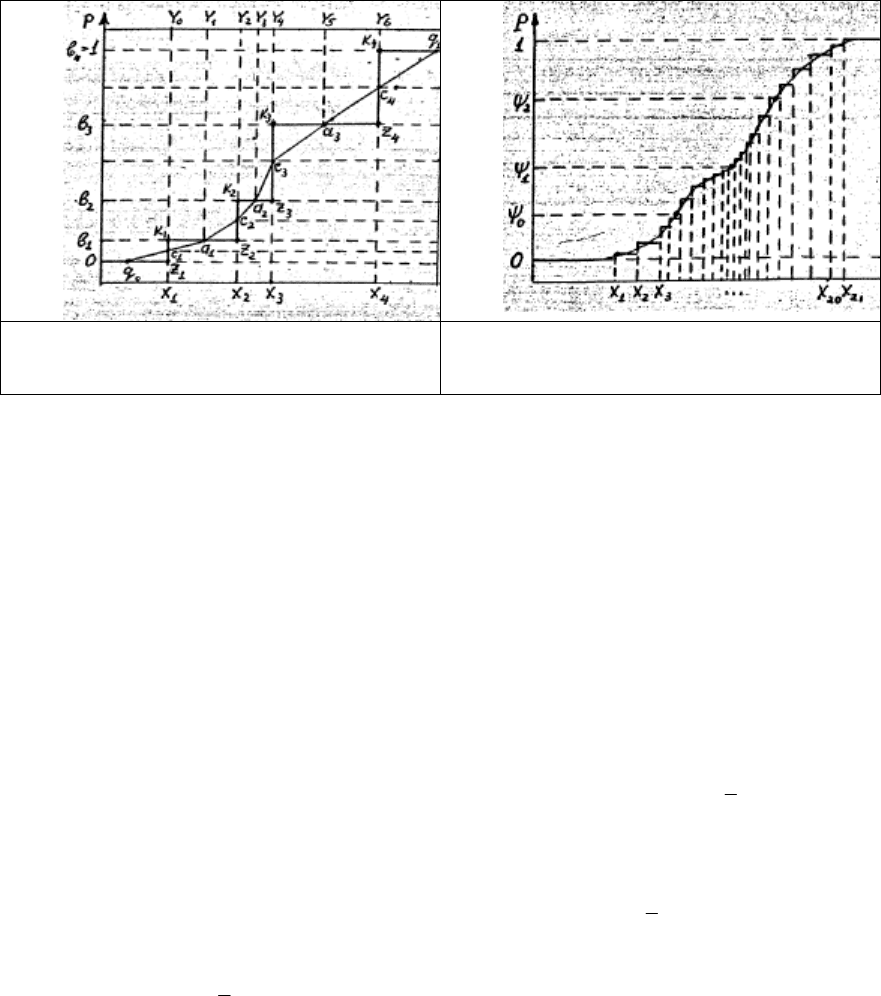
5
Рис. 3. Кусочно-линейная сплайн-
функция (9), построенная на Б – сетке (18):
N = 4 точки, К = 6 узлов.
Рис. 4. Кубический сплайн (8),
построенный на М – сетке:
N = 21 точка, К = 3 узла.
Для построения М-сетки можно использовать правила Уолда («выбирайте как можно
меньше узлов - так, чтобы на каждом интервале было не меньше четырех - пяти наблюдений;
следите за тем, чтобы на каждом интервале было не более одной точки перегиба; помещайте узлы
Ψ
i
ближе к точкам перегиба» [11, с. 142], см. Рис. 4), наши рекомендации [5-7; Р6.1]; значения Ψ
i
можно оценивать наряду с остальными коэффициентами сплайн - функции методом нелинейного
регрессионного анализа [12; П4Р6.1.1].
Выбор структуры сплайн - функции.
Хорошо ли, когда все гладко? Это - вопрос скользкий. (Из интернета)
Нa Р
Н
- сетке (16) может быть построена кусочно-постоянная сплайн-функция (6),
аппроксимирующая функцию распределения F
Э
(X) (β
i
= C
i
, Ψ
i-1
= X
i
, Z = X; Рис. 1) и обратную
функцию распределения
(
)
1
Э
FP
−
(β
i
= X
i+1
- X
i
, Ψ
i-1
= b
i
, Z = P, P ∈ (0; 1), Рис. 1)
На Р
П
- и Б – сетках строятся кусочно – линейные аппроксимации Ф
Δ
(
β
, Р) (7) или (9)
обратной функции распределения
(
)
1
Э
FP
−
.
На Р
П
– сетке эта функция (рис. 2) состоит из отрезков прямых на ломаной линии q
0
- C
2
- C
3
-
q
1
, а на Б – сетке q
0
- α
1
- C
2
- α
2
- C
3
- α
3
- q
1
(Рис. 3)
Отрезки (q
0
C
1
) и (C
4
q
1
) являются экстраполяцией функции Ф
Δ
(
β
, Р) за пределы области
наблюдений (X
1
, X
N
).
Ограничение интервалом значений (X
-
, X
+
) этой функции можно учесть путем обрезания
аппроксимации Ф = Ф
Δ
(
β
, Р), например, такого:
X = X
-
I
10
(Ф,X) + Ф П(X
-
, X
+
, X) + X
+
I
01
(Ф, X). (20)
В этом случае функция
(
)
1
Э
FP
−
нa Р
П
- сетке будет состоять из отрезков прямых на ломаной
линии. Например, на Рис. 2:
f
1
- f
2
- C
2
- C
3
- f
3
- f
4
. (21)
(Для предотвращения сбоев на ЭВМ границы X
-
, X
+
рекомендуется раздвигать на малую
величину ξ порядка 10
-5
(X
+
- X
-
) [5; Р6.1.1]).
Сравнение рассмотренных выше и описанных в литературе [7] способов кусочно-линейной
аппроксимации эмпирической функции распределения по частным критериям качества -
погрешности аппроксимации и сложности формулы показывает, что наименее сложной и
достаточно точной является сплайн-функция (9) на Б - сетке (18) при малом объеме выборки (2 ≤
N ≤ 8 ) и на Р
П
– сетке (17) - при большом объеме (8 ≤ N ≤ 100); при очень большом объеме
выборки (N > 100) лучше использовать кубическую сплайн-функцию (8) на М – сетке Уолда.
Замечание.
Преимущество использования сглаженной ЭФРВ проявляется и при
изображении
эмпирической функции плотности вероятностей (ЭФПВ) распределения изучаемых величин в
6
виде гистограммы (см. пример 2 в разделе 2). Неряшливый вид такой гистограммы (с
«зубчиками») существенно зависит от числа и положения интервалов, на которые разбиваются
данные выборки [1, 14.15] (соответственно меняются ширина, высота и расположение
«зубчиков»). Результаты обработки данных лучше сразу представлять в виде ЭФРВ в
доверительных границах для заданного (чаще всего - нормального) распределения (см. пример 5 в
разделе 2). Но если всё же необходимо для наглядности привести в отчёте (или рекламе)
изображение ЭФПВ распределения выборки (такова традиция [1]), то её график легко получить
путём дифференцирования аппроксимации ЭФРВ сплайн-функцией (8). Получается красиво. Но
главное, что такое построение не зависит от числа и положения интервалов, на которые
разбиваются данные выборки.
1.3.3 Расчет статистических оценок.
В математике нет символов для неясных мыслей. ( Анри Пуанкаре)
В качестве мер положения распределения СВ Х будем вычислять медиану и среднее
взвешенное значение.
Медиану вычисляют путем подстановки значения Р = 0,5 в ОФР СВ Х:
(
)
1
05
05
, Э
ˆ
XFP,
−
==; (22)
среднее
LL
11
iii
ii-
xxgg
=
=
∑∑
(23)
(Напомним: i - индексы, L - объем исходной выборки {x
i
, g
i
}; g
i
– веса точек x
i
).
В качестве меры разброса СВ X будем использовать устойчивую S и эффективную S
x
оценки.
Устойчивая к выбросам оценка S вычисляется как полуразность γ - квантилей:
()()
(
)
1212
2
//
Sxx/
ρρ+−
=−
, (24)
где
ρ
- заданная вероятность; γ
∈
{(1 +
ρ
)/2; (1 -
ρ
)/2}, x
(1 -
ρ
)/2
и x
(1 +
ρ
)/2
- нижняя и верхняя
границы области 100
ρ
-процентных допустимых значений СВ Х (не путать с границами ДИ!).
Значения этих границ вычисляются по формуле
(
)
1
э
XFP
−
= (25)
путем подстановки вместо P значений (1 -
ρ
)/2 и (1 +
ρ
)/2 соответственно.
Кроме того, вычисляется взвешенное среднеквадратичное отклонение (BCO):
()
(
)
05
2
11
1
,
ПП
ii
xi
ii
Sgxxg
==
=−−
∑∑
. (26)
При нормальном распределении CB X, X ~ N(
ν
,
σ
) (с центром
ν
и СО
σ
) статистики
05
,
ˆ
X
и
X
являются оценками центра
ν
, а S (при
ρ
= 0,68) и S
х
- оценками СО
σ
.
Уровень значимости
ˆ
α
, нижнюю
()
12
н
B/
ˆˆ
ϕϕ
−
=
и верхнюю
()
12
в
B/
ˆˆ
ϕϕ
+
=
интервальные
оценки с заданной доверительной вероятностью В определяют (по Эфрону) численным методом
статистических испытаний (Монте-Карло [4]).
Расчет интервальных статистических оценок.
Никогда не выявляйте в программе ошибки, если не знаете, что с ними делать дальше.
(Из интернета)
Исходные данные: N - объем выборки;
(
)
1
э
XFP
−
= - аппроксимация обратной функции
распределения СВ Х; ϕ = ϕ({x
i
}) - вид заданной статистики (По умолчанию ϕ
(
•
)
- медиана. В
качестве
ϕ
{x
i
} могут быть также заданы: среднее
X
, меры разброса S, S
x
, или любая другая
статистика.); B - доверительная вероятность; У - указание на расчет оценок (У = 0) или проверку
гипотез (У = 1) (по умолчанию У = 0); M - число циклов (по умолчанию М = 10
4
);
ε
ϕ
- малое число
(по умолчанию ε
ϕ
= 10
-4
).
Последовательность действий.

7
1. Задается номер цикла j = 1.
2. Генерируется N раз значения
j
i
P
величины P, равномерно распределенной на отрезке (0,
1) (
1
i,N
= ). Для генерирования P
i
∈[0, 1] можно использовать алгоритм
12
4
iiiii
Pt/;tUU,
==+
если
12
4
ii
UU;
+<
12
41
iiiii
Pt/;tUU,
==+−
если
12
4
ii
UU;
+≥
U
1(i+1)
= U
2i
; U
2(i+1)
= t; U
10
= 3,14159; U
20
= 0,5421. (27)
3. По формуле
(
)
1
э
XFP
−
=
значения
j
i
P
преобразуются в значения
j
i
XImX
∈ .
4. По формуле
{
}
j
ji
X
ϕϕ=
вычисляется одно значение
ϕ
j
статистики
ϕ
.
4.1. Если
ϕ
{x
i
} - медиана, или устойчивая оценка CO S (24), то осуществляется
предварительная обработка данных {x
i
}; строится кусочно-линейная аппроксимация ОФР
(
)
1
j
T
FP
−
и вычисляется одно значение
05
,j
ˆ
X
или одно значение S
j
.
4.2. Если ϕ{x
i
} - среднее
X
или CO S
x
, то вычисляется одно значение
j
X
или S
xj
.
5. Расчеты по п. 1 - 4 повторяют M раз.
6. По формуле (6) строится кусочно-постоянная аппроксимация
(
)
1
э
FP
ϕ
−
= обратной
функции распределения статистики
ϕ
(
β
i
=
ϕ
i+1
-
ϕ
;
ψ
i-1
= B
i
; Z = P).
7. Подставляют значения P = (В - 1)/2 и Р = (В + 1)/2 в формулу
(
)
1
э
FP
ϕ
−
=
и вычисляют
нижнюю
н
ˆ
ϕ
и верхнюю
в
ˆ
ϕ
границы ДИ параметра φ.
1.3.4 Проверка гипотез методом доверительных интервалов.
Всякая вещь есть форма проявления беспредельного разнообразия. (К. Прутков)
Результаты интервального оценивания m параметров нередко представляют на графиках в
виде 100B-процентных («традиционно» В = 0,95) ДИ. Обычно эти m интервалов просто
иллюстрируют ошибки измерения. Между тем эффективность статистической обработки данных
можно повысить, если одновременно с интервальным оцениванием выполнять проверку гипотез о
равенстве оцениваемых параметров друг другу методом доверительных интервалов (ДИ). Для
этого задают критическое значение уровня значимости
α
к
и строят интервальные оценки с
некоторой доверительной вероятностью В, зависящей от α
к
и т [Р1.2].
Эта зависимость в неявном виде получена в работе [13] для m нормально распределенных
случайных величин с равными дисперсиями:
2
0,5
Z
P/2
= Z
α/m(m-1)
; B = 1 - P, (28)
где Z
γ
- верхний
γ
-предел нормированного нормального распределения,
γ ∈ {P/2; α/m(m - 1)}; α = α
к
.
Выразим зависимость В от
α
к
и т в явном виде. Используем для этого аппроксимацию
Сливняка зависимости Z
γ
от вероятности γ [14, Ф(19.1)Р1]
Z
γ
= 1,94{-lg[4
β
(1 -
β
)]}
0,5
;
β
∈
(0; 0,5) (29)
и, наоборот [Ф(19)Р1],
P = 1 – [1 – exp(-0,6118
2
2
P/
Z
)]
0,5
. (30)
После простых подстановок получаем:
B = (1 – (4
β
(1 -
β
))
0,5
)
0,5
;
β
=
α
к
/(m(m – 1)). (31)
Например, при «обычном» уровне значимости
α
к
= 0,06 получим зависимость доверительной
вероятности В от числа m оцениваемых параметров:
m 2 3 4 5 6 7 10 13
и т. д.
B 0.81 0.89 0.93 0.94 0.95 0.96 0.97 0.98
и т. п.
Для величин с отличными от нормального закона распределениями и разными дисперсиями
метод ДИ дает результаты тем приближённее, чем больше названные отличия. Тем не менее, если
при разглядывании пары сравниваемых ДИ видно, что они перекрываются большими своими
частями, или наоборот, отстают очень далеко друг от друга, то соответствующие выводы о
принятии гипотезы Н
0
о равенстве сравниваемых параметров, или её отклонении, очевидны. Если
8
даже ДИ перекрываются своими малыми частями, или не перекрываются, но отстоят друг от друга
довольно близко, то при необходимости уточнить результаты проверки гипотезы Н
0
могут быть
использованы другие методы [15].
Литература.
1. Гласс Д., Стэнли Д. Статистические методы в педагогике и психологии. / Пер. с англ.
под ред. Ю. П. Адлера. - M.: Прогресс, 1976г - 496 с.
2. Алимов Ю. И. О практической ценности теории оценок. - Автоматика, 1981, № 2, с.
84-94.
3. Эльясберг П. Е. Измерительная информация: сколько её нужно? Как её
обрабатывать? – М.: Наука, 1983.- 208 с.
3. Акопов М. Г. О критике Ю. И. Алимовым метода математический статистики.
Автоматика, № 2, (1982), с. 82-87.
4. Эфрон Б. Нетрадиционные методы многомерного статистического анализа. Сб.
статей. - М.: Финансы и статистика, 1988.- 263 с.
5. Новик Ф. С., Цейтлин H. А., Авраменко Э. H. Некоторые способы кусочно-гладкой
аппроксимации функций. - // Заводская лаборатория. - 1981. - №1. - С. 48 - 55.
6. Едвабник И. Ю., Новик Ф. С., Цейтлин Н. А. Аппроксимация сложных физико-химических функций с
помощью двухсторонних сплайнов. Рукопись деп. в ОНИИТЭХИМ г. Черкассы 11 мая 1984 г. №912ХII-Д84
26 с. - Библ. ук. ВИНИТИ Деп. рукописи 1985 №1, с.147 I, 6 авт. 0,05.
7. Едвабник И. Ю., Новик Ф. С., Цейтлин Н. А. Использование двухсторонних сплайнов для
аппроксимации сложных физико-химических кривых. Зав. лаб., 1985, т.51, №3, с. 54-57.
8. Кендалл М. Д., Стьюарт А. Теория распределений. - М.: Наука, 1966. - 588 с.
9. Цейтлин Н.А. Статистическая обработка выборки из одномерной случайной
величины, НИОХИМ, Харьков, 1980, 31 с. (Рукопись деп. в ОНИИТЭХИМ г. Черкассы 25
января 1979 г. №1049ХР-Д80) – Библ. указатель ВИНИТИ Деп. рукописи, 1980, №11, с.
97.
10. Ежов А. И. Вычисление рядов распределений. М.: Статистика, 1973.- 158 с.
11. Пуарье Д. Эконометрия структурных изменений (с применением сплайн - функций).
/ Пер. с англ. В. В. Минахина. - M.: Финансы и статистика, 1981. - 184 с.
12. Химмельблау Д. Анализ процессов статистическими методами. -М.: Мир, 1973, 948
с.
13. Цейтлин Н. А. Проверка гипотез методом доверительных интервалов. В кн. Методы
математической статистики в основной химии. Труды, T. 55, НИОХИМ, Харьков, 1981, с.
82-89.
14. Цейтлин Н. А. Применение методов математической теории эксперимента в
содовой промышленности. Обзорная информация. Серия «Содовая пром.». - М.:
НИИТЭХИИ, 1984. - 48 с.
15. Холлендер М. Вулф Д. Непараметрические методы статистики. - M.: Финансы и ст-
ка, 1983. - 520 с.
1
2. Статистическая обработка одномерной выборки
Факты - упрямая вещь, но статистика гораздо сговорчивее. Лоренс Питер
Многие люди считают себя «специалистами» по обобщению результатов наблюдений.
Часто подобное «обобщение» делается с помощью средних величин…
Пример 1. Допустим, в фирме работает n = 99 человек и все получают одинаковую
зарплату У (пусть для ровного счёта У = 1000 евро в месяц), а один из них - директор - получает
в 100 раз больше, то есть 100У. По расчётам подобных «специалистов» в среднем на одного
человека приходится зарплаты (nУ +100У)/100 = 1,99У. Получается, что работники фирмы
получают «в среднем» не так уж и плохо – по 1990 евро в месяц! Вот вам и обобщение «в
среднем»!
Давайте посмотрим, скажем, что пишут в средствах массовой информации о
продолжительности жизни населения разных стран: «в Германии средняя продолжительность
жизни 78,2 года, в Японии – 81,5». Верно ли теперь, что мы получили представление о
соотношении продолжительности жизни населения в упомянутых странах? Неверно! Может,
просто в Японии больше очень старых людей или смертность новорожденных меньше, чем в
Германии!?
Очевидно, что подобное «обобщение» результатов наблюдений приводит к
поверхностным суждениям. Для науки и практики (и даже для «широкого» читателя) следует
сравнивать кривые распределения вероятностей сопоставляемых случайных величин!
Пример 2.
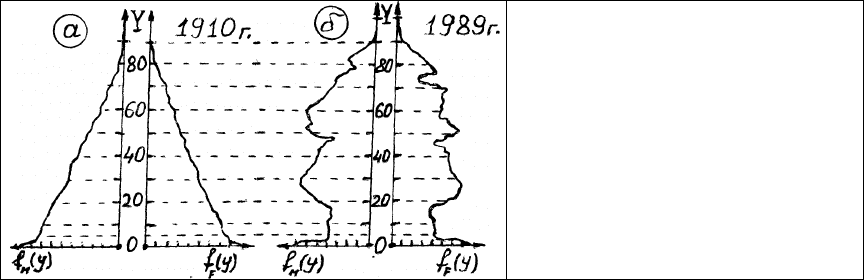
Рассмотрим кривую распределения возраста населения Германии (Рис.1).
Рис.1. Распределение возраста
жителей Германии в разные годы:
а – 1910 г.; б – 1989 г.; Y – возраст,
лет; f
м
(у) и f
F
(у) – функции
плотности вероятностей
распределения возраста для мужчин
и женщин, соответственно.
Нормальному закону распределения величина возраста человека не подчиняется. Все, что
можно сделать с изображёнными распределениями - это сравнивать их друг с другом, так
сказать, „непосредственно“ по частям - по усмотрению специалистов. Тогда мы можем
сопоставить, например, возраст групп людей в определённых (заинтересованными
специалистами – акушерами, педиатрами, педагогами, военными, врачами, геронтологами,
историками, социологами, страхователями жизни, пенсии и др.) временных интервалах
(новорожденных, малышей и т. д., вплоть до престарелых), разных полов, исторических
периодов и т. п. Сопоставление приведенных кривых может дать много полезной информации
вдумчивому читателю. А средняя величина – повторим - это всего лишь абстрактная точка,
одна из нескольких математических характеристик положения всего распределения! Здесь
уместно заметить, что упомянутыми «характеристиками положения» могут быть и такие
«средние» как (средняя геометрическая, гармоничная, квадратичная), а также медиана, мода и
др. [1, 2]. О месте этих параметров в статистическом анализе мы поговорим позже.
В процессе статистической обработки одномерной выборки из множества значений
случайной величины возникает ряд проблем, решение которых не настолько формализованы,
чтобы эту работу можно было полностью доверить вычислительной машине. Часто

2
исследователю приходится задумываться над каждым этапом расчётов и принимать решение с
учётом специфических особенностей конкретного исследования.
Важно подчеркнуть, что при сравнении М случайных величин
(
)
1,
i
YiM
=
следует
сравнивать между собой непосредственно их распределения - функции плотности
вероятности f
i
(у) [или функции распределения F
i
(у)]. Если сравниваемые функции
распределения описываются одинаковыми параметрическими функциями
(
)
,,1,
i
i
FyiM
θ = , где
i
θ
- вектор параметров i-того распределения, то в этом случае
сравнивать можно и векторы
i
θ
, имея в виду все же главную задачу: сравнение
вероятностных распределений непосредственно!
2.1. Применение нормального закона распределения выборки
Будем обрабатывать результаты измерения свойств в метрических шкалах. Определенное
представление о СВ можно получить путем статистической обработки представительной
одномерной выборки. Часто предполагается, что исследуемая СВ распределена по нормальному
закону. Вместе с тем на практике, в зависимости от природы изучаемого явления, встречаются
различные законы распределения. В случае отклонения закона распределения от нормального
иногда можно подобрать некоторую «нормализующую функцию преобразования», позволяющую
перейти к новой случайной величине, распределенной приближенно нормально.
Аппроксимация распределения нормальным законом позволяет свернуть (сократить)
информацию о СВ, пользоваться унифицированными методиками интервального оценивания и
проверки параметрических гипотез.
Кроме подбора нормализующего преобразования при статистической обработке
одномерной выборки приходится решать проблему выбросов, проверять независимость
генерального среднего от порядкового номера наблюдений, а также согласие выборочного
распределения с теоретическим, оценивать параметры нормального распределения.
Решению перечисленных задач посвящены цитируемая работа [1] и настоящий раздел.
(Помнится, что, рекомендуя рукопись работы [1] к печати, рецензент В. Д. Смоляк в
шутку назвал её “Повесть о нормальном распределении”.)
2.1.1. Выбор нормализующего преобразования
Выборка из одномерной случайной величины Y имеет вид
{
}
YImy;y
i
N
1i
i
∈
=
, (1)
где y
i
- действительные числа; N - объем выборки.
Пусть выборка
{
}
N
1i
i
y
=
является результатом наблюдений, лишенных систематической
погрешности. Рассмотрим подмножество
{
}
N
1i
i
z
=
множества Im Z, каждый элемент z
i
которого
получен некоторым преобразованием
(
)
•
ϕ
соответствующих элементов y
i
множества Y, причем
(
)
,Im,1,
iii
zyzZiN
ϕ=∈=
. (2)
Свертка информации об изучаемой случайной величине сводится к вычислению всего
двух выборочных моментов - среднего
z
ˆ
z
=
ν
и дисперсии
2
z
2
z
s
ˆ
=σ
. Эти моменты и объем
выборки N будут достаточны для описания распределения СВ Z, если нам удастся показать, что
множество
{
}
N
1i
i
z
=
является выборкой из ImZ, где величина Z распределена по нормальному
закону, то есть
(
)
2
zz
,N~Z σν с функцией распределения вероятности
()()
2
0,5122
(2)exp0,5;0;
z
zzzz
Fzzdzπσνσσ
−−−
−∞
=−−≥
∫
|z| <
∞
. (3)
К значениям y величины Y, возвращаются с помощью обратного преобразования
(
)
1
yz
ϕ
−
= . (4)
3
При выборе преобразования (2) можно использовать представления о природе выборки
{
}
N
1i
i
y
=
. Распределение большинства случайных величин аппроксимируется нормальным законом
(3). Например, распределение случайных ошибок измерения, суммы независимых, случайно
распределенных переменных и многих других (например, описанных ниже) величин, имеющих
незначительный разброс с унимодальным, симметричным относительно моды графиком
плотности распределения. Тогда просто принимают z
i
= y
i
. Если y
i
- площадь поверхности или
частота редких событий, то
5,0
ii
yz = . Если y
i
- объем, то
31
ii
yz = [2, с. 70]. Для величин y
i
,
ограниченных слева нулем {прирост величин, толщина отложения инкрустаций на поверхностях
химических аппаратов [3], диаметр пылинок в выхлопных газах [1, с. 39], скорость оседания
частиц, концентрация веществ в растворе вблизи нуля и другие величины, график плотности
распределения которых унимодальный (одновершинный), крутой слева (со стороны минимума
выборки) и пологий справа (со стороны максимума выборки) [2, с. 104]
}
, используют
преобразование
(
)
0ii
yylgz
+
=
, где y
0
- параметр сдвига, такой, что 0yy
0i
>
+
; часто
принимают y
0
= 0. Если Y - доля (часть целого, например, КПД, концентрация вещества в смеси и
т. п.); 0 < y
i
< 1 и значения y
i
заполняют большую часть интервала (0,1), или если значения y
i
заполняют малую часть интервала (0,1), но расположены близко к 0 или к 1, то «нормализующим»
может быть преобразование Фишера [2, с. 247]
5,0
ii
yarcsinz =
или Ланцберга
(
)
1ylgz
1
ii
−−=
−
.
Два последних преобразования имеют вид s-образной кривой на интервале (0,1). Аналогичным
свойством обладает и сама функция (3). Для удобства вычислений подставим в уравнение (3)
(
)
1
zz
zz
νσ
=− и аппроксимируем его алгебраической формулой Сливняка [4]
()
{
}
0,5
1
1,94lg41;01
zkyyy
=−−<<
, (5)
где k = 1 при y > 0,5 и k = -1 при y < 0,5 (или то же самое - в виде ступенчатой
аппроксимации
(
)
0,50,5
kyy=−−
при y
≠
0,5); индексы i опущены.
Выполним соответствующее обратное преобразование:
(
)
0,5
2
1
0,50,512,303exp0,2657ycz
=+−−
, (6)
где c = 1 при z
1
> 0 или с = -1 при z
1
< 0 (или то же самое - в виде
11
czz
= при z
1
≠
0).
Если значения долей y
i
близки только к 0 или только к 1, более просты преобразования,
соответственно,
5,0y0,ylgz
iii
<
<
−
=
, и
(
)
1y5,0,y1lgz
iii
<
<
−
−
=
. Если Y - зависящая от
времени переменная, то
ii
y1z
=
[2, с. 468]. Применяют также преобразования
2
i
5,1
i
5,0
i
y,y,y
−
и
др. [2, с. 467]. Хороший пример использования нормализующего преобразования данных выборки
в токсиколого-гигиенических исследованиях см. в работе [19].
2.1.2. Выявление выбросов
На ошибках мучаются. (Из интернета)
Выбросом является результат наблюдения, наиболее резко отклоняющийся от среднего
значения и не принадлежащий генеральному распределению СВ (речь по-прежнему идёт о
нормальном распределении СВ).
Мерой расстояния результата измерения z
i
от среднего значения
z
является нормированное
отклонение
(
)
N,1i,szz
zii
=−=ζ ,
(7)
где СО s
z
вычисляется по всем N точкам совокупности:
()()
0,5
2
1
1.
N
zi
i
szzN
=
=−−
∑
(8)
