Цейтлин Н.А. Из опыта аналитического статистика
Подождите немного. Документ загружается.

14
Гипотеза Н
0
(46) отвергается на уровне значимости
0K
α
, если D
N
> К
N,α
и не отвергается в
противном случае. Критические значения верхних
α
- пределов К
N,α
распределения Колмогорова
находят по таблицам в справочниках [6, 7, 18 и др.].
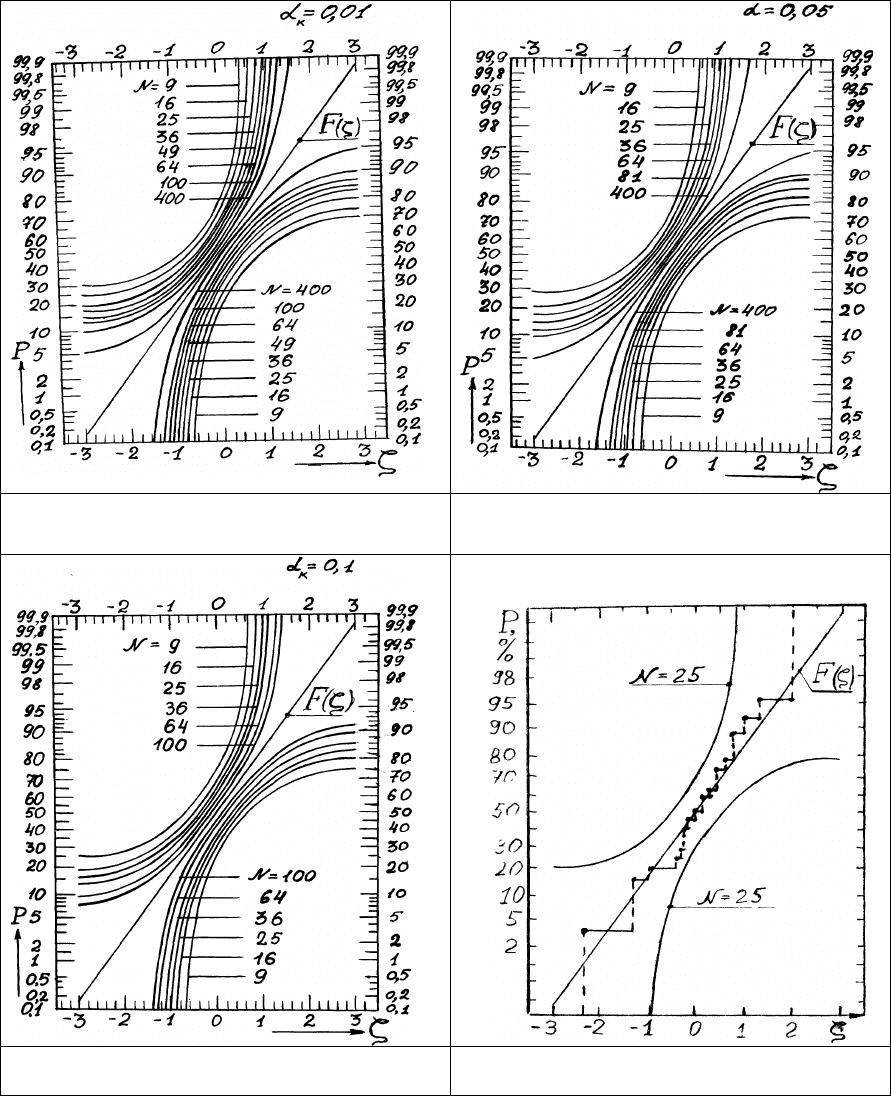
Графический метод.
Наглядно продемонстрировать результат проверки гипотезы о согласии выборочного и
нормального распределений по критерию Колмогорова можно с помощью заранее
подготовленных номограмм (рис. 4 - 6).
Рис. 4. Границы доверительных интервалов при
уровне значимости
0K
α
= 0,01
Рис. 5. Границы доверительных интервалов
при уровне значимости
0K
α
= 0,05
Рис. 6. Границы доверительных интервалов при
Рис. 7. Демонстрация согласия выборочного
F
N
(z) и логнормального F(z) распределений
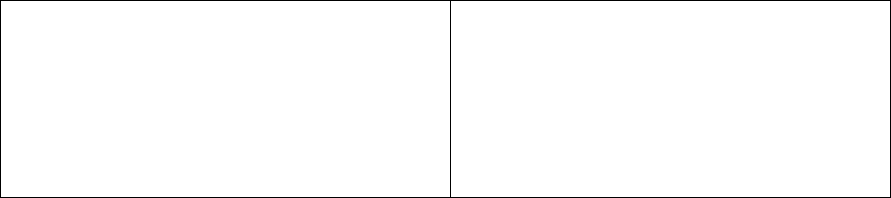
15
уровне значимости
0K
α
= 0,1
На рис. 4 - 6 обозначено: Р – вероятность;
ζ
- нормированная и центрированная нормально
распределённая случайная величина (7);
0K
α
= 0,01 -критическое значение уровня
значимости.
толщины слоя отложения солей
(к примерам 3 - 5 ):
Р – вероятность;
ζ
- нормированная и
центрированная нормально распределённая
случайная величина (7);
0K
α
= 0,01 – заданное
критическое значение уровня значимости.
Для наглядной демонстрации результата проверки гипотезы о согласии выборочного F
N
(z) и
нормального F(z) распределений на «вероятностной бумаге» изображается график теоретической
функции F(
ζ
) нормированного нормального распределения случайной величины
ζ
. Ось ординат
(Р) преобразована так, чтобы S – образная функция (3), где z =
ζ
,
ν
= 0 и
z
σ
= 1 приобрела вид
прямой линии. Над и под графиком функции F(
ζ
) изображены верхняя и нижняя границы 100(1-
0K
α
)%-ного доверительного интервала для F(
ζ
) при определённом объёме выборки N.
Построения.
1) Задают критический уровень значимости
0K
α
(см. [Т2Р1]) и выбирают соответствующую
номограмму из рис. 4 - 6.
2) Вариационный ряд (44) преобразуют в соответствующий ряд
121
iiN
ζζζζζ
+
≤≤≤≤≤≤
KK, (56)
элементы
i
ζ
которого вычисляют по формуле (7).
3) Подставляя в формулу (53) значения
i
ζ
из вариационного ряда (56), строят на избранной
номограмме ступенчатую кумулятивную кривую. Если эта кривая целиком расположена между
соответствующими числу N верхней и нижней границами доверительного интервала, то гипотеза
Н
0
(46) о согласии выборочного и нормального распределений не отвергается, в противном случае
она отвергается.
Пример 5. По данным примеров 3 и 4 необходимо наглядно продемонстрировать результат
проверки гипотезы о согласии выборочного и нормального распределений толщины слоя
отложения солей.
Решение. Воспользуемся графическим методом.
1) Задаём критический уровень значимости
α
k0
= 0,01. 2) Вариационный ряд (44)
преобразуем в соответствующий ряд (56):
1
ζ
= (lg1 - 0,712)/0,3 = -2,3;
2
ζ
= -1,3 и т. д.;
25
ζ
= 2.
3) Строим на номограмме (рис. 4) ступенчатую кумулятивную кривую, которая оказалась
целиком расположенной между границами ДИ (рис. 7), что и требовалось продемонстрировать.
Литература.
1. Цейтлин Н. А. Статистическая обработка выборки из одномерной случайной величины. НИОХИМ,
Харьков, 1980 31 с. (Рукопись деп. в ОНИИТЭХИМ г. Черкассы 25 января 1979 г. № 1049ХР-ДШ)- Библ.
указатель ВИНИТИ Деп. рукописи, 1980, № 11, 97 с.
2. Закс Л. Статистическое оценивание. - M.: Статистика, 1976. - 600 с.
3. Цейтлин Н. А. Расчет толщины слоя отложений бикарбоната натрия на внутренней поверхности
карбонизационной колонны содового производства. Депон. рукопись № 498/75 деп. г. Черкассы, 1976 г. (Ре-
ферат в РЖ «Химия», 1976, реф. 16. л. 38, 12 с.)
4. Цейтлин Н. А. Применение методов математической теории эксперимента в содовой
промышленности. Обзорная информация. Серия «Содовая пром-сть». - М.: НИИТЭХИМ, 1984. - 48 с.
5. ГОСТ 11.002-73. Правила оценки анормальности результатов наблюдений. – М.: Изд.
стандартов, 1973. - 24 с.
6. Большев Л. H., Смирнов H. В. Таблицы математической статистики. - M.: Наука, 1965. - 464 с.
7. Идье В. и др. Статистические методы в экспериментальной физике. / Пер. с англ. под ред. А. А.
Тяпкина. - M.: Атомиздат, 1976. – 335 с.
8. Эфрон Б. Нетрадиционные методы многомерного статистического анализа. Сб. статей. - М.: Финансы
и статистика, 1988.- 263 с.
16
9. Подборка статей по бутстрепу / Заводская лаб. 1987., Т. 53. - Вып. 10. С.76 - 99.
10. Орлов А.И. /Заводская лаборатория. 1987. Т. 53. - Вып. 10. С.82-85.
11. Бокс Д., Дженкинс Г. Анализ временных рядов, прогноз и управление. Вып. 1. - М.: Мир, 1974. - 406
с.; вып. 2. М.: Мир, 1974. - 198 с.
12. ГОСТ 11.006-74. Правила проверки согласия опытного распределения с теоретическим. - M., Изд.
Стандартов, 1975. 24 с.
13. Сборник научных программ на Фортране. Руководство для программиста. Вып. 1. Статистика. /
Пер. с англ. С. Я. Виленкина. - M.: Статистика, 1974. - 316 с.
14. ГОСТ 11.004-74. Прикладная статистика. Правила определения оценок и доверительных границ для
параметров нормального распределения. - M., Изд. Стандартов, 1974. - 20 с.
15. Гласс Д., Стэнли Д. Статистические методы в педагогике и психологии. / Пер. с англ. под ред. Ю. П.
Адлера. - M.: Прогресс, 1976г - 496 с.
16. Пасхавер И. С. Средние величины в статистике. – М.: Статистика, 1979. – 279 с.
17. Колмогоров А. Н. Избранные труды.: Математика и механика. - М.: Наука, 1985. - с. 136-138.
18. Мюллер П., Нейман П., Шторм P. Таблицы по математической статистике / Пер. с нем. В. М.
Ивановой. - M.: Финансы и статистика, 1982. - 272 с.
19. Шитиков В.К., Тихонов В.Н., Быков С.Т., Ковалев А.Ф. Статистический анализ и нормальность
распределения выборок в токсиколого-гигиенических исследованиях // Гигиена и санитария, N 3,1985. С. 61-
62.

2.2. Применение логистического закона распределения выборки
Лингвистический принцип использования сельскохозяйственного орудия на поверхности не
сжимающейся жидкости J (Вилами по воде писано)
Настоящая работа защищена в качестве дипломного проекта студенткой Харьковского
Государственного Университета им. А. М. Горького Акимовой Юлией Александровной
(руководитель проекта: к. т. н. Цейтлин Н. А.).
Аннотация
Для получения аппроксимационных формул, необходимых при оценивании
статистических параметров СВ, распределенных по логистическому закону,
производились следующие работы:
- предпринята попытка аналитического решения поставленной задачи;
-
составлен алгоритм, позволяющий путем имитации выборки численным методом
Монте - Карло получить верхние α-пределы аналогов распределения Стьюдента и
Фишера для СВ, имеющих логистическое распределение;
- рассчитаны значения для таблицы верхних
α
-пределов z
α
нормированного
логистического распределения;
- произведено уточнение коэффициентов формулы Рокицкого для аппроксимации
обратной функции распределения Стьюдента;
Для вычисления коэффициентов в аппроксимационных формулах использован
раздел ППП Regression Analisys приложения STATISTICA for Windows-95.
Список сокращений
ДИ - доверительный интервал;
МДИ -
метод доверительных интервалов;
МО - математическое ожидание;
СВ - случайная величина;
СО - среднеквадратичное отклонение;
ФР - функция распределения;
Предисловие
Идея использовать простые формулы логистического распределения принадлежала
профессору А. И. Орлову. Автор решил воспользоваться этой идеей, чтобы «одним
выстрелом убить трёх зайцев»: 1) - помочь студентам освоить принципы
интервального оценивания и проверки статистических гипотез на простом примере; 2) -
получить представление о степени соответствия и точности двух практически
одинаковых статистических методов; 3) сделать уважаемому коллеге Александру
Ивановичу подарок – реализацию его идеи.
Введение
При оценивании статистических параметров СВ основное внимание уделяется
обычно величинам, имеющим нормальное распределение. Однако встречаются случаи,
когда выборка заведомо не подчиняется нормальному закону распределения, а какому -
либо другому закону. Например, в экономических исследованиях иногда используется
логистическое распределение [10]. Логистическая функция распределения очень мало
отличается от нормальной функции распределения и наряду с последней используется, в
частности, в медико-биологических исследованиях для анализа эффекта действия
различных лекарств, ядов и так далее [11]. Кроме того, А. И. Орлов [5] нашёл, что при
объеме выборки, меньшем 2000 единиц, различие между нормальным и
логистическим распределениями незначимо. Это позволяет, по его мнению, в
подобных случаях использовать вместо нормального распределения логистическое.

Такое стремление связано с тем, что логистическая функция распределения имеет
простую математическую форму [10, с. 151]
()()
{
}
1
1exp -
X
Fxxνβ
−
=+
,
β
≠
0,
∞
<
x . (1.1)
Это распределение симметрично относительно значения x =
ν
, которое является
математическим ожиданием (МО) СВ. Дисперсия такой СВ равна
π
2
β
2
/3 и, следовательно,
среднеквадратичное отклонение (СО) есть 3πβ , а величина коэффициента эксцесса
(четвертого центрального момента)
α
4
= 4,2. Хотя значение
α
4
в этом случае отличается
от значения
α
4
для нормального распределения (при котором
α
4
= 3), логистическое
распределение очень похоже на нормальное в большей части диапазона с тем же самым
МО, а СО на 1/15 больше, чем у нормального. Так что логистическое распределение во
многих случаях можно использовать вместо нормального.
В литературе логистическому распределению уделяется скромное внимание.
Методы интервального оценивания статистических параметров и проверки гипотез,
основанные на логистическом распределении СВ, не развиты.
Целью настоящей работы была попытка довести идею А. И. Орлова до
логического конца - создать средства, позволяющие осуществлять интервальную оценку
статистических параметров и проверку параметрических гипотез в предположении о
логистическом законе распределения СВ.
Работа излагается в сокращённом виде.
2.2.1. ИССЛЕДОВАНИЕ ЛОГИСТИЧЕСКОГО РАСПРЕДЕЛЕНИЯ
Бинарный характер высказываний индивидуума женского пола, утратившего с возрастом
социальную значимость J (Бабушка надвое сказала).
Функция логистического распределения имеет вид (1.1); плотность распределения
вероятностей
p
X
(x) =
{}
{
}
{}
2
1exp()//exp()/
xx
νββνβ
−
+−−
,
∞
<
x
; (1.2)
МО СВ X
()
{}
()
{}
+
2
-
()x1 + exp - x/exp - xdx
MX νββνβ
∞
−
∞
=
∫
.
После замены t = (
ν
- x)/
β
(1.3)
получаем
()()
+
- 2 2
tt
-
()1 + edt+ e1dt
tt
MXteeβν
+∞∞
−
−∞∞
=−+
∫∫
. (1.4)
Поскольку
()
2
t
te1dt = 0
t
e
+∞
−
−∞
+
∫
и
()
+
2
t
-
e1dt1
t
e
∞
−
∞
+=
∫
, (1.5)
получаем M(X) =
ν
.
Для вычисления дисперсии СВ X по формуле
(
)
(
)
(
)
[
]
(
)
22
2
2
XMXMXMXD ν−=−=
(1.6)
вычислим интеграл
()
()
22
dx
X
MXxxp
+∞
−∞
=
∫
.
Используя подстановку (1.3), получим
()()()()
2 2 2
22tt22t
e1dt - 2te1dt +te1dt
ttt
MXeeeννββ
+∞+∞+∞
−−−
−∞−∞−∞
=⋅+⋅⋅+⋅⋅+
∫∫∫
.
С учетом (1.3), (1.4) формулу (1.6) можно переписать в виде

()
()
∫
∞
+
∞−
−
+⋅⋅= dte1etXD
2
tt22
β
. (1.7)
В формуле (1.7) сделаем подстановку y = e
t
.
Далее рассмотрим вспомогательную функцию
()
()
dy
y1
y
zf
0
2
1z
∫
∞
+
−
+
=
. Функция f(z)
является B – функцией, f(z) = B (z, 2-z), так как по определению
B(p, q) =
()
1
0
dt
1
p
pq
t
t
+∞
−
+
+
∫
. (1.8)
Рассмотрим производные
()()
2
1
0
(lny) 1dy
z
fzyy
+∞
−
−
′
=+
∫
и
()()
2
21
0
(lny) 1dy
z
fzyy
+∞
−
−
′′
=+
∫
.
В данном случае правомерность дифференцирования является следствием
соответствующих свойств B - функции (1.8).
Таким образом,
()
()
()
z - 2 z, B
1
z
2
2
0
2
2
dz
d
= 1f =dy
y1
yln
=
′′
+
∫
∞
+
.
Далее,
=−+=−=
−
=− ))z1(1(Г)z(Г)z2(Г)z(Г
)2(Г
)z2(Г)z(Г
)z2,z(B
= Г(z)⋅(1 – z)⋅Г (1 - z)=
(
)
z sinz - 1
π
π
⋅
. (1.9)
Найдем
()
z2 ,z B
1
z
2
2
dz
d
−
=
, пользуясь (1.6):
(
)
(
)
()
(
)
()
1-z sin
1z
z 1sin
z1
z sin
z1
1 z
→
−
⋅
=
−
−
⋅
=
−
⋅
→
π
π
π
π
π
π
(
)
()() ()
()
z 1
33
3
1
116 + 1
z
zzoz
π
ππ
→
⋅−
→
⋅−−⋅−−
() ()
(
)
22
2
1161
zozπ=+⋅−+−
,
то есть мы получили ряд Тейлора для функции g(z) =
(
)
(
)
1-z sin1z
π
π
−
⋅
.
Следовательно,
(
)
2
6 1 2
gπ
′′
= и окончательно
(
)
(
)
2222
22
=
63
1
, 2 = = 2
sin
1 1
dd
dzdz
z
Bzz
z
zz
ππ
π
π
−
−
==
.
Таким образом, наш интеграл
()
- 2
22
0
(lny)1+ydy = 3
π
+∞
∫
.
Возвращаясь в формулу (1.7), получаем D(X) = π
2
β
2
/3, а СО СВ X
()
- 0,5
DX = 3
L
σπβ= .
В дальнейшем удобно использовать нормированное логистическое распределение
СВ Х
(
)
L
X - MX
3( - )
L
X
U
ν
σπβ
==
.
Теперь M(U
L
) = 0, D(U
L
) = 1.
Плотность распределения вероятностей для U
L
()
2
1 u u
exp1exp, u <
33
L
U
pu
ππ
β
−
=−+−∞

Введем обозначения: X
∼
L (
ν
,
2
L
σ
) - логистическое распределение СВ X;
X ∼ L (0, 1) - нормированное логистическое распределение СВ X.
Вычислим функцию распределения для U
L
:
()
(
)
2
xx
U
- -
1 u u
x = du = exp1exp
33
p
L
L
U
Fudu
ππ
β
−
∞∞
−+−
∫∫
.
После несложной замены переменных и подстановки пределов интегрирования,
получим окончательный результат
()
{
}
1
- 1
L
x = 1exp 3
L
U
Fxπ
σ
−
+−
.
Функция нормированного логистического распределения (при ν = 0, β =
π3
)
()
{
}
1
x = 1exp3; x <
L
U
Fxπ
−
+−∞
, (1.10)
а функция плотности вероятностей
()
{
}
{}
2
3exp3
u = , u <
1 + exp3
L
U
u
u
p
ππ
π
−
∞
−
. (1.11)
Последующие действия были направлены на получение формулы функции
плотности для аналога распределения Стьюдента, основанного на логистическом
законе, путем аналитических расчетов. С этой целью, по аналогии с нормальным
случаем, предполагалось найти функцию плотности квадрата СВ Z (U
L
= Z
2
), имеющей
нормированное логистическое распределение, затем получить характеристическую
функцию, соответствующую этой функции плотности.
Из общих свойств СВ [1] известно, что характеристическая функция суммы
независимых СВ равна произведению характеристических функций слагаемых. Если
ξ
1
, ...
, ξ
n
- независимые СВ с характеристическими функциями
ϕ
1
(t), ϕ
2
(t), ... , ϕ
n
(t), то
характеристическая функция
ϕ
(t) суммы
ξ
1
+ ... +
ξ
n
есть
ϕ
(t) =
ϕ
1
(t)
⋅ϕ
2
(t)
⋅
...
⋅ϕ
n
(t). Таким
образом, зная вид характеристической функции для плотности распределения квадрата
одной СВ, подчиненной логистическому закону, можно найти характеристическую
функцию для суммы квадратов N таких величин. Так как распределение однозначно
определяется своей характеристической функцией [1], получим выражение, описывающее
плотность распределения
χ
2
, основанного на логистическом законе распределения СВ.
Функция плотности аналога распределения Стьюдента рассчитывается как плотность
распределения отношения двух СВ ξ/η, где ξ распределена по логистическому закону с
параметрами (0, 1), а η имеет распределение аналогичное χ
2
в нормальном случае.
Итак, рассмотрим СВ ξ. Её функция распределения F (x) =P(ξ ≤ x).
Затем рассмотрим функцию
η
=
ξ
2
. Величина
η
всегда неотрицательна и при y > 0
соотношение
η
≤
y эквивалентно соотношению – y
0.5
≤
η
≤
y
0.5
. Поэтому
η
имеет функцию
распределения
0.50.5
( y ) = F ( y ) - F ( - y ) npu y
0 u ( y ) = 0 npu y < 0.
GG≥
Тогда функция плотности вероятности величины η имеет вид
(
)
(
)
(
)
- 0.50.50.5
( y ) = G( y ) = 0.5y y - - y npu
y 0 u ( y ) = 0 npu y < 0
gffg
′
≥ .
Таким образом, если СВ Z обладает функцией распределения
()
{
}
1
z = 1exp 3,
Z
Fzπ
−
+−
то плотность распределения ее квадрата U
L
= Z
2
имеет вид
{
(
)
2
0.5
( z ) = - exp3
z3
gz
π
π
−×
(
)
(
)
(
)
}
- 1 1
1+exp- 3exp31+exp3zzzπππ
−
×−
,
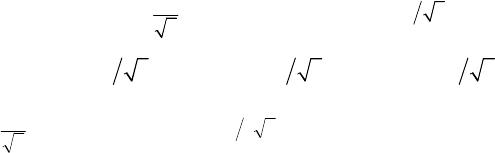
а соответствующая характеристическая функция
()
()
+
2
0
( t ) = - exp i t z{exp 3
3
z
π
ϕπ
∞
⋅⋅−⋅×
∫
(
)
(
)
(
)
- 1- 1
1+exp - 3- exp 31+exp 3} dz
zzzπππ
×⋅⋅⋅⋅
;
иначе,
()
()
dz 32zch2z t i exp
3
- = ) t (
2
+
0
2
⋅⋅⋅⋅
−
∞
∫
π
π
ϕ
.
Однако получить аналитические выражения для функций распределения
χ
2
и
Стьюдента, основанных на логистическом законе распределения СВ, нам не удалось и
продолжать работу по намеченному ранее плану оказалось невозможным.
Поэтому далее решено было воспользоваться численным методом Монте - Карло [2]
для вычисления верхних α-пределов аналогов распределения Стьюдента и Фишера.
Метод Монте - Карло в широком смысле определяется как любой способ решения
модели, в котором используются случайные или псевдослучайные числа. В данном случае
будет рассматриваться решение так называемой модели выборок.
2.2.2. РАСЧЕТ ЗНАЧЕНИЙ ВЕРХНИХ α-ПРЕДЕЛОВ РАСПРЕДЕЛЕНИЙ
СТЬЮДЕНТА И ФИШЕРА, ОСНОВАННЫХ НА ЛОГИСТИЧЕСКОМ ЗАКОНЕ
Амбивалентная природа нейронных импульсов, испускаемых корой головного мозга J
(И хочется, и колется).
Предварительно требуется получить выборку значений СВ, имеющих
распределение, аналогичное распределениям Стьюдента и Фишера (хорошо изученным
для нормально распределенных СВ) для логистического распределения с заданным
числом степеней свободы.
Предполагается решать эту задачу следующим образом.
1. Рассмотрим процедуру получения выборки СВ, имеющей заданное распределение.
Для этого воспользуемся методом обращения.
Обозначим функцию распределения СВ X через F(x), то есть
P(X < x) = F(x). (2.1)
Если F(x) - непрерывная возрастающая функция, то существует обратная функция,
обозначенная X=F
-1
(Y). Значения X
i
можно выбирать из распределения F(x
i
) с помощью
обратной функции F
–1
и случайных чисел Y
i
, лежащих в интервале [0; 1], а именно
X
i
= F
-1
(Y
i
). (2.2)
Из (2.2) следует, что
P(X < x
i
) = P[F
-1
(Y
i
)
< x
i
] = P[Y
i
< F(x
i
)] = F(x
i
), (2.3)
где последнее равенство следует из характеристики случайных чисел: если Y
i
(i = 1, 2, ...)
есть случайные числа, то их функция распределения удовлетворяет следующему
уравнению для всех i:
F(Y
i
) = P(Y
i
< y
i
);
(
)
i
Y =
F
ii
y npu 0y1
≤≤
;
(
)
i
Y =
F
i
0 npu y1
<
и
(
)
i
Y =
F
i
1 npu y1
>
. (2.4)
Заметим, что теоретически случайные числа должны быть непрерывными
переменными с функцией плотности, определяемой выражением
()
i
fy
=
i
1npu 0y1;
≤≤
и
()
i
fy
=
0 при всех остальных значениях у. (2..5)
В данном случае генератор случайных (точнее, псевдослучайных) чисел Y
i
,
равномерно распределенных на отрезке [0; 1], имеет следующую схему [4]
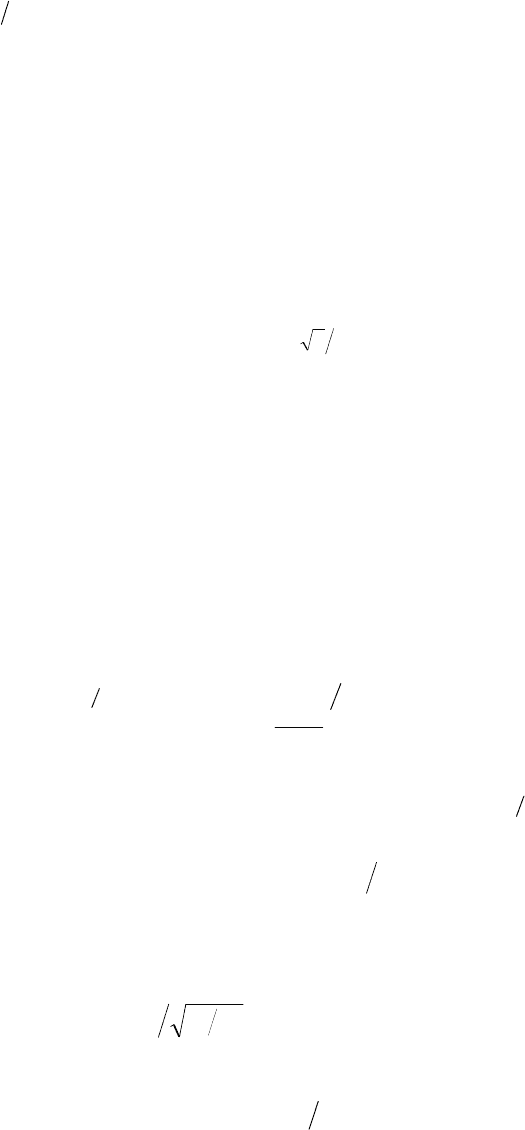
1 i2 i1 i2 i1 01 ( i + 1)2 i
i
1 i2 i1 i2 i202 ( i + 1) i
u + u, npu u + u< 4; u = 3,1415
9; u= u;
= t4; =
u + u - 4,npu u + u4; u = 0,54210,
u= t.
ii
Yt
≥
(2.6)
Порождаемые таким образом числа для практических целей можно считать
случайными, равномерно распределенными в интервале [0; 1] и независимыми.
Из вышесказанного следует, что выборку неравномерно распределенных СВ,
подчиняющуюся любому заданному закону распределения, можно получить путем
выбора случайных чисел, распределенных равномерно, и использования их затем в
качестве ординат заданной функции распределения вероятностей. Величины
соответствующих абсцисс представляют собой числа, распределенные по заданному
закону.
Как отмечалось выше, логистическое распределение (1.1) симметрично
относительно значения x = ν, которое является МО СВ, подчиненных этому закону.
Дисперсия равна π
2
β
2
/3. Таким образом нормированное и центрированное логистическое
распределение (при значениях
ν
= 0,
β
=
3π
и z = (x -
ν
)/
β
) описывается формулой
(1.10).
Согласно методу обращения, получим выражение для СВ, распределенной
логистически с параметрами M = 0 и D = 1, где M - МО, а D - дисперсия:
Z
i
= -3
0.5
π
-1
ln(Y
i
/(1 - Y
i
)) (2.7)
2.2.2.1. Расчет значений верхних
α
-пределов аналога распределения Стьюдента.
Отсутствие регресса в метаболизме организма млекопитающих при увеличении отношения
жиров к углеводам в традиционном блюде оседлых народов J (Кашу маслом не испортишь).
Рассмотрим статистику
t = mN
0.5
/S
Z
, (2.8)
где
N
i
i = 1
m = ZN
∑
,
()()
0.5
N
2
i = 1
= 1
Zi
SZmN
−−
∑
, N - объем выборки.
Случайные величины Z
i
(
)
i = 1, N
имеют логистическое распределение,
нормированы и центрированы. В общем случае, если все Z
i
подчинены одному и тому же
логистическому закону распределения, то величина
N
i
i = 1
m = ZN
∑
также распределена
логистически. Тогда (m – M(m))/σ
Z
(σ
Z
= σ/N
0.5
)
имеет логистическое распределение с
параметрами M = 0 и D = 1. Отношение
(
)
22
Z
S1N σ⋅−
имеет распределение, аналогичное
χ
2
в нормальном случае с N – 1 степенями свободы, так как включает в себя сумму
квадратов N разностей
()
2
N
i =1
- m
i
Z
∑
, связанных между собой соотношением
()
N
i =1
- m = 0
i
Z
∑
.
Рассмотрим СВ fV U = t , где U имеет логистическое распределение с
параметрами M = 0 и D = 1, а V подчиняется закону распределения
χ
2
с f степенями
свободы. Подставив наши выражения вместо U и V, получим
t = [(m – M(m))/σ
Z
]/[
(
)
22
1
Z
NS
σ
−
(N–1)
–1
]
0.5
= [m – M(m)]N
0.5
/S
Z
.
(2.9)
Поскольку мы рассматриваем логистическое распределение с параметрами M = 0 и
D = 1, то M(m) = 0 и
σ
= 1. Таким образом, величина t имеет распределение, аналогичное
распределению Стьюдента с N–1 степенями свободы (f = N–1).
Опишем алгоритм получения значений верхних
α
-пределов аналога
распределения Стьюдента (то есть значений t
f,
α
величины t таких, что P(t
f
> t
f,
α
) =
α
)
для числа степеней свободы f:

1) генерировать N случайных чисел Y
i
, равномерно распределенных на отрезке [0;
1] (N = f + 1);
2) воспользовавшись формулой (2.2), получить выборку объемом N элементов
значений СВ Z
i
, распределенных по заданному закону;
3) вычислить значение величины t согласно (2.8);
4) операции 1, 2, 3 повторить M раз;
5) из полученных значений t
i
(
)
i = 1, M
организовать вариационный ряд,
упорядоченный по возрастанию членов;
6) задать значения α
∈
(0.25, 0.1, 0.05, 0.025, 0.01);
7) для каждого значения α из ряда выбрать элемент с порядковым номером (1–α)M.
Согласно методу Монте – Карло, этим элементом и является искомый верхний
α
-предел
аналога распределения Стьюдента.
2.2.2.2. Расчёт верхнего
α
-предела аналога распределения Фишера
Идентичность вкусовых характеристик растения семейства крестоцветных и овощной
культуры средней полосы России J (Хрен редьки не слаще).
Аналогичным образом воспользуемся статистикой
2
x
2
xf ,f
2121
SS = F
;
()()
∑
−−
1
1
N
1
=
i
1
2
1i
2
x
1NmZ = S
;
()
()
∑
−−
2
2
N
1 =j
2
2
2j
2
x
1NmZ = S
, (2.10)
где
∑
1
N
1
=
i
1i1
NZ = m
,
∑
2
N
1 =j
2j2
NZ = m
Эта статистика имеет распределение, аналогичное F – распределению Фишера в
нормальном случае с числом степеней свободы числителя f
1
и знаменателя - f
2
.
Если величины U и V независимы и каждая из них распределена как χ
2
с f
1
и f
2
степенями
свободы соответственно, то отношение
F
f
1
2
, f
= (U/f
1
)/(V/f
2
) распределено по
закону Фишера. Тогда отношение
(
)
[
]
(
)
[
]
2
22
2
x2
2
11
2
x1
NS1NNS1N
21
σσ ⋅⋅−⋅⋅−
(2.11)
будет распределено как
F
f
1
2
, f
, если рассматриваются случайные выборки объемом N
1
и
N
2
из логистически распределенных совокупностей с дисперсиями
σ
1
2
и
σ
2
2
;
S
x
1
2
и
S
x
2
2
обозначают
выборочные дисперсии. В нашем случае
σ
1
= 1 и
σ
2
= 1.
Алгоритм получения верхних α-пределов величины
F
f
1
2
,, f
α
для заданных
чисел степеней свободы f
1
и f
2
построен аналогично алгоритму получения значений
верхних α-пределов величины t
f
.
1) генерировать N
1
и N
2
случайных чисел Y
i
, равномерно распределенных на отрезке
[0; 1] (N
1
= f
1
+ 1; N
2
= f
2
+ 1);
2) воспользовавшись формулой (2.2), получить две выборки из N
1
и N
2
СВ,
распределенных по заданному закону;
3) вычислить значение величины
F
f
1
2
, f
согласно (2.10);
4) операции 1, 2, 3 повторить M раз;
5) из полученных значений
F
f
1
2
,, f i
(
)
i = 1, M
организовать вариационный
ряд, упорядоченный по возрастанию членов;
6) задать значения
α
∈
(0.05, 0.025, 0.01);
