Цейтлин Н.А. Из опыта аналитического статистика

Подождите немного. Документ загружается.

3.6.3. Линейный однофакторный регрессионный анализ

Главный порок математиков - применение греческих букв при первой же возможности.

(Из интернета)

Обычно исследователь предполагает, что ИФР (6.2) является монотонной или непрерывно

дифференцируемой функцией аргумента. Существование изломов или экстремумов на ней требует

физической интерпретации. В принципе, ИФР может быть любая линия, проходящая в пределах

доверительного "коридора". Поэтому изломы на ЭЛР, построенной методом скользящей средней,

которые носят случайней характер (см., например, рис. 1 и 4), не нуждаются в физической

интерпретации.

Гладкая линия, проведенная, например, "от руки" в пределах доверительного "коридора",

может служить исследователю ориентиром при подборе алгебраического выражения для

аналитической аппроксимации (приближения) функции регрессии (6.2) [18]. Во многих случаях

такой линией оказывается прямая, соответствующая самой простой - линейной модели регрессии

Y =

X +

, (6.8)

где

– коэффициенты регрессии (

часто называют «свободным членом»);

~ N(0,

) -

случайная ошибка модели (6.8);

- СО отклика Y. Для нас по-прежнему важно не столько

оценить параметры

модели (6.8), сколько построить доверительный интервал для ИФР.

Замечание. В большинстве инженерных работ исследователя интересует поведение

функции регрессии (6.2), а не её коэффициенты. Однако, иногда целью исследования может быть

оценка параметров (например,

модели (6.8)), которые могут иметь определённый

физический смысл. В этом случае важно совместное интервальное оценивание этих параметров

[18].

Эффективные оценки параметров линейной регрессионной модели

В математике нет символов для неясных мыслей. (Анри Пуанкаре).

Пусть в результате измерения значений y

отклика Y при фиксированных значениях x

фактора X получена выборка {x

}; i =

N,1

. Она позволяет найти эффективные однозначные

оценки параметров

линейной регрессионной модели (6.8) [16]:

(

)

(

)













−−==

∑∑∑∑∑

=====

xxNyxyxNb

111

; (6.9)

(

)

Nxbyb

∑

−==

100

β ; (6.10)

()()

5,0

ˆˆ













−−==

∑

NyyS

iiYY

σ , (6.11)

где

- результат расчета отклика с помощью эмпирической функции регрессии (ЭФР,

которая является однозначной оценкой истинной функции регрессии):

= b

+ b

x; (6.12)

- остаточное СО отклика Y (S

называют также «СО остаточной ошибки ЭФР», а

квадрат остаточного СО, S

– «остаточной дисперсией»).

Вместо непосредственного расчёта S

по формуле (6.11) проще использовать выражение

(

)

()

[

]

5,0

2−−−=

∑∑∑

===

NyxbybyS

. (6.13)

Пример 12. Зависимость остаточной концентрации взвеси Y от удельной нагрузки X при

осветлении сточных вод после очистки газа доменных печей в гидроциклоне - флокуляторе [23]

представлена выборкой {x

} (i =

1,5

1 1 1 1 1

2 2 4 4 4

3 1 3 9 1

4 3 12 16 9

5 3 15 25 9

Сумма

∑

10 35 55 24

Здесь x

- значения нагрузки, м

/(м

⋅ч); y

- концентрация взвеси в осветленной воде, 10

мг/дм

Предполагается, что зависимость Y от X описывается линейной регрессионной моделью

(6.8). Найти эффективные оценки параметров этой модели.

Решение. Рассчитаем произведения x

, квадраты

x и

y исходных значений и их суммы

(см. табличку). Воспользовавшись формулами (6.9), (6.10) и (6.13), получаем b

= (5⋅35 -

⋅

10)/(5

⋅

55 - 15

) = 25/50 = 0,5; b

= (10 - 0,5

⋅

15)/5 = 0,5; S

= [(24 - 0,5

⋅

10 - 0,5

⋅

35)/3]

0,5

= 0,707.

Проверим последний результат непосредственно по формуле (6.11):

= [(0

+ 0,5

+ 1

+ 0,5

+ 0

)/3]

0,5

= 0,707.

Ответ. ЭФР имеет вид

= 0,5 + 0,5x (рис. 6); СО остаточной ошибки S

= 0,707.

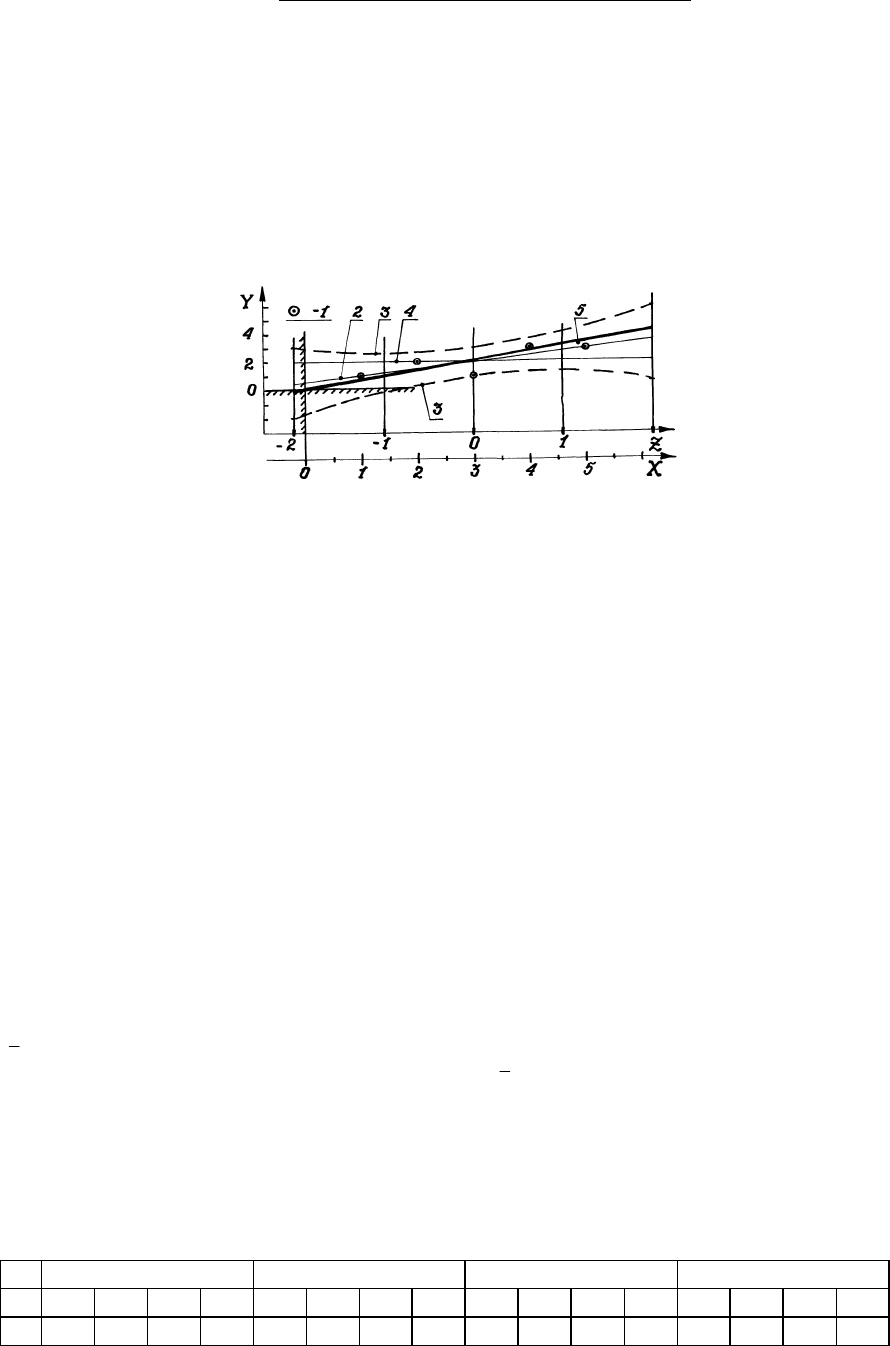
Рис. 6. Регрессия остаточной концентрации взвеси Y (100

мг/дм

) по нагрузке X (м

/м

ч) при

осветлении сточных вод после очистки газа (промежуточный результат обработки данных

примера 12):

1 - результаты измерений; 2 – график ЭФР y

= 0,5 + 0,5x; 3 - границы 95%-го доверительного

интервала; 4, 5 - варианты истинной линии регрессии; Z - нормированное отклонение фактора X.

Замечание. Часто в литературе ЭФР называют «уравнением регрессии». Однако

«уравнением» ЭФР бывает «временно», когда она записывается в виде системы из N уравнений c

известными факторами и откликами, и k неизвестными коэффициентами. Эти коэффициенты

затем находят методом наименьших квадратов (обычно). Окончательно уравнение регрессии

становится ЭФР.

Эффективная интервальная оценка истинной линии регрессии

Интервальная оценка ИФР [13] задается нижней

YН

и верхней

YВ

границами

доверительного интервала (ДИ)

YН

= y

∆

;

YВ

= y

∆

, (6.14)

где

- однозначная оценка (6.19) ИЛР;

∆

- полуразмах ДИ;

∆

= Ф(Z,

, N)S

, или, короче,

∆

= ФS

; (6.15)

сомножитель Ф зависит от значения величин Z,

и N;

Ф = Ф(Z,

, N) = t

f;α/2

[1/N + Z

/(N - 1)]

0,5

; (6.16)

величина Z показывает число значений СО S

фактора Х, откладываемое от его среднего значения

Z = (x -

)/S

; (6.17)

f;α/2

- число Стьюдента, которое можно определять по номограмме [рис. 4Р1] в зависимости от

уровня значимости

и числа степеней свободы f; здесь f = N - 2.

Для быстрых расчётов вместо формулы (6.16) удобнее пользоваться табл. 3.

Таблица 3

Значение функции Ф(Z,

, N) = t

N-2;α/2

[1/N + Z

/(N - 1)]

0,5

для построения интервальной оценки

прямолинейной регрессии

= 0,1

= 0,05

= 0,01

= 0,001

N Z = 0

Z = 1

Z = 2

Z = 3

Z = 0

Z = 1

Z = 2

Z = 3

Z = 0

Z = 1

Z = 2

Z = 3

Z = 0

Z = 1

Z = 2

Z = 3

3 3,64 5,76 9,64 13,9 7,33 11,6 19,4 27,9 36,8 58,1 97,2 140 367 581 972 1400

4 1,45 2,23 3,67 5,26 2,15 3,28 5,41 7,75 4,96 7,58 12,5 17,9 15,8 24,1 39,8 57,0

5 1,05 1,57 2,57 3,68 1,42 2,13 3,48 4,98 2,61 3,91 6,39 9,14 5,77 8,66 14,1 20,2

6 0,87 1,29 2,09 2,98 1,13 1,68 2,72 3,89 1,87 2,78 4,52 6,45 3,51 5,21 8,46 12,1

7 0,76 1,12 1,81 2,58 0,97 1,43 2,31 3,29 1,52 2,24 3,62 5,16 2,59 3,82 6,18 8,80

8 0,68 1,00 1,62 2,30 0,86 1,26 2,04 2,90 1,31 1,91 3,09 4,40 2,10 3,08 4,97 7,07

9 0,63 0,92 1,48 2,10 0,78 1,14 1,84 2,62 1,16 1,70 2,73 3,89 1,80 2,62 4,22 6,01

10 0,58 0,85 1,37 1,95 0,72 1,05 1,70 2,41 1,06 1,54 2,47 3,51 1,59 2,31 3,71 5,28

11 0,55 0,80 1,28 1,82 0,68 0,98 1,58 2,25 0,97 1,41 2,27 3,23 1,44 2,08 3,34 4,75

12 0,52 0,75 1,21 1,72 0,64 0,93 1,48 2,11 0,91 1,32 2,11 3,00 1,32 1,91 3,06 4,35

13 0,49 0,71 1,15 1,63 0,61 0,88 1,40 2,00 0,86 1,24 1,98 2,82 1,23 1,77 2,84 4,03

14 0,47 0,68 1,09 1,55 0,58 0,83 1,34 1,90 0,81 1,17 1,88 2,66 1,15 1,66 2,65 3,77

15 0,45 0,65 1,05 1,49 0,55 0,80 1,28 1,81 0,77 1,11 1,78 2,53 1,08 1.56 2,50 3,55

16 0,44 0,63 1,01 1,43 0,53 0,77 1,23 1,74 0,74 1,06 1,70 2,42 1,03 1,48 2,37 3,37

17 0,42 0,61 0,97 1,38 0,51 0,74 1,18 1,68 0,71 1,02 1,63 2,32 0,98 1,41 2,26 3,21

18 0,41 0,59 0,94 1,33 0,49 0,71 1,14 1,62 0,68 0,98 1,57 2,23 0,94 1,35 2,16 3,07

19 0,39 0,57 0,91 1,29 0,48 0,69 1,10 1,56 0,66 0,95 1,51 2,15 0,90 1,30 2,07 2,94

20 0,38 0,55 0,88 1,25 0,46 0,67 1,07 1,51 0,64 0,92 1,46 2,03 0,87 1,25 2,00 2,83

21 0,37 0,54 0,86 1,21 0,45 0,65 1,04 1,47 0,62 0,89 1,42 2,01 0,84 1,21 1,93 2,73

22 0,36 0,52 0,83 1,18 0,44 0,63 1,01 1,43 0,60 0,86 1,38 1,95 0,82 1,17 1,86 2,65

23 0,35 0,51 0,81 1,15 0,43 0,62 0,98 1,39 0,59 0,84 1,34 1,90 0,79 1,13 1,81 2,56

24 0,35 0,50 0,79 1,12 0,42 0,60 0,96 1,36 0,57 0,82 1,30 1,85 0,77 1,10 1,76 2,49

26 0,33 0,47 0,76 1,01 0,40 0,57 0,91 1,30 0,54 0,78 1,24 1,76 0,73 1,04 1,66 2,36

32 0,29 0,42 0,67 0,90 0,36 0,51 0,81 1,15 0,48 0,09 1,10 1,55 0,64 0,91 1,45 2,06

42 0,25 0,36 0,58 0,81 0,31 0,44 0,31 0,44 0,41 0,59 0,94 1,33 0,54 0,77 1,23 1,75

62 0,21 0,30 0,47 0,65 0,25 0,36 0,57 0,80 0,33 0,47 0,76 1,07 0,43 0,62 0,98 1,39

102

0,16 0,23 0,36 0,54 0,19 0,27 0,44 0,62 0,26 0,36 0,58 0,82 0,33 0,47 0,75 1,06

202

0,11 0,16 0,26 0,35 0,13 0,19 0,31 0,43 0,18 0,25 0,40 0,57 0,23 0,33 0,52 0,74

402

0,08 0,11 0,18 0,26 0,09 0,13 0,21 0,31 0,12 0,18 0,28 0,40 0,16 0,23 0,37 0,52

Пример 13. По данным примера 12 построить интервальную оценку линейной регрессии

(6.8) с доверительной вероятностью 1 -

= 0,95.

Решение

1. Воспользовавшись вспомогательной табличкой решения примера 12, найдем по формуле

(4.2);

= 15/5 = 3; по формуле (4.3): S

= [(55 - 15

/5)/4]

0,5

= 1,6.

2. С помощью формулы (6.15) и табл. 3 определим

∆

= 1,42

⋅

0,707 = 1,00 при Z = 0;

∆

= 1,5

при Z = 1;

∆

= 2,46 при Z = 2.

3. Восстанавливаем перпендикуляры к оси X в точках Z = -2; -1; 0; 1 и 2 (см. рис. 6).

4. От точек пересечения этих перпендикуляров с ЭФР откладываем вверх и вниз значения

полуразмахов, соответственно,

∆

5. С помощью лекал строим верхнюю и нижнюю границы ДИ с доверительной

вероятностью 1 -

= 0,95.

Быстрый метод "натянутой нити"

Kaк бы кpoпoтливo и тщaтeльнo вы ни гoтoвили выбopку, вaм вceгдa мoгут cкaзaть, чтo oнa

нeпpaвильнa и нeпpимeнимa к дaннoй пpoблeмe. (Чeтвepтый зaкoн пpoвepки Паркинсона)

Воспользуемся старым методом однозначного оценивания линейной регрессии. Натянутую

нить (как в древности) или прозрачную линейку с изображением прямой линии на нижней

поверхности (как теперь) кладем на график (см., например, рис. 6) так, чтобы экспериментальные

точки равномерно располагались по обе стороны от прямой [20]. При x = 0 ордината точки

пересечения этой прямой с осью Y является значением коэффициента b

; коэффициент b

∆

x, где

∆

x - приращение фактора;

∆

y - соответствующее приращение отклика на прямой.

Удобно выбирать

∆

x = 10

, где n - целое число (например,

∆

x = 10

= 1, или 10

= 10 и т. п.).

Прямые, полученные методом "натянутой нити" незначимо отличаются от прямых (12),

найденных эффективным методом по формулам (6.9) и (6.10). Метод, "натянутой нити" не только

простой и быстрый, но имеет даже некоторые преимущества по сравнению с эффективным

методом. Некоторых экспериментаторов гипнотизирует термин «эффективный метод» (слово

«эффективный» означает «действенный» [28]), в то время как в данном контексте «эффективный

метод» - это математический термин. Эффективный метод - "слепой", так как экспериментатор не

"ощущает" влияния чисел, входящих в уравнения (6.9) и (6.10); эффективный метод чувствителен

к резко отклоняющимся точкам; при эффективном оценивании параметров моделей вида (6.8),

полученных из нелинейных по коэффициентам регрессии моделей путем замены переменных

(например, нелинейную модель Y

= εβ

′′′

)(

x заменяют линейной моделью (6.8), где Y = lgY

; β

= lg

′

; x = lgx';

= lg

'), появляются значимые систематические ошибки [18]! Использование в

последнем случае других эффективных методов (метода Лелянова [25, с. 177], нелинейного или

линейного взвешенного метода наименьших квадратов [18]) требует громоздких вычислений.

А теперь напомним читателю ещё раз, что

в статистической обработке данных

построение однозначной оценки регрессии – полдела. Дело венчает интервальная оценка!

Быстрое интервальное оценивание линейной регрессии

Экcпepимeнт мoжнo cчитaть удaвшимcя, ecли нужнo oтбpocить нe бoлee 50% cдeлaнныx

измepeний, чтoбы дocтичь cooтвeтcтвия c тeopиeй. (Зaкoн Maйepca)

Воспользуемся быстрой линейной однозначной оценкой регрессии (то есть, прямой,

полученной методом «натянутой нити»).

Определения. Невязкой (или остатком)

−

называется разность между эксперименталь-

но найденным значением отклика y

и его значением

на ЭФР (см., например, Рис 6).

Размахом невязок w

называется сумма значений максимальной

(

)

yyw

max −=

минимальной

(

)

(

)

ˆˆ

minmax

iiii

wyyyy

=−=−

невязок:

= w

+ w

(

)

(

)

yyyy

−

max

max . (6.18)

Интервальную оценку линейной регрессии строим по формуле (6.14), а полуразмах

∆

вычисляем по формуле

∆

= Ф

(Z,

, N) w

, или, короче,

∆

= Ф

(6.19)

где сомножитель Ф

зависит от значения величин Z,

и N так:

= Ф

(Z,

, N) = k

N-2;α/2

[1/N + Z

/(N - 1)]

0,5

. (6.20)

Значение числа k

N-2;α/2;

(точнее, верхнего

/2-предела k

N-2;α/2

) в зависимости от значений

N - 2 находим в табл. 2; значение Z определяем по формуле (6.17), в которой значение S

вычисляем по формуле (5.1). Для быстрых расчётов вместо формулы (6.20) можно пользоваться

величиной Ф из табл. 3. Тогда Ф

= Ф k

N-2;α/2

Быструю оценку остаточного СО отклика вычисляем по формуле

= w

N-2

; (6.21)

коэффициент a

N-2

находим в табл. 2.

Пример 14. По данным примера 12 построить быстрые однозначную и интервальную (с

доверительной вероятностью 1-

= 0,95) оценки линейной регрессии (6.8). Оценить СО

остаточной ошибки отклика.

Решение. С помощью метода «натянутой нити» получим быструю оценку аналитической

линии регрессии (она почти совпадает с линией 2 на рис. 6). По формуле (6.18) определяем

= 0,5 + 1 = 1,5; по формуле (5.1) и табл. 2 находим S

' = (5 - 1)/2,33 = 1,7; по формулам (6.19),

(6.20) и табл. 2

∆

= 1,5⋅1,3/5

0,5

= 0,87 при Z = 0;

∆

= 1,95(1/5 + 1/4)

0,5

= 1,3 при Z = 1;

∆

1,95(1/5 + 1)

0,5

= 2,1 при Z = 2; по формуле (6.21) S'

= 1,5/1,69 = 0,89; по формуле (5.1) S'

= (5 -

1)/2,33 = 1,72. Используя технику графического построения интервальной оценки линейной

регрессии, описанную в п. 3 - 5 решения примера 13, получаем ДИ, который почти совпадает с

границами 3 на рис. 6, найденными эффективным методом.

Упражнение 1.

Пусть результаты наблюдений представлены выборкой {x

}; i =

N,1

, где

N = 13 точек (Рис. 7). Необходимо построить прямолинейную ЭФР и 95-% - ный доверительный

интервал для ИФР быстрым методом.

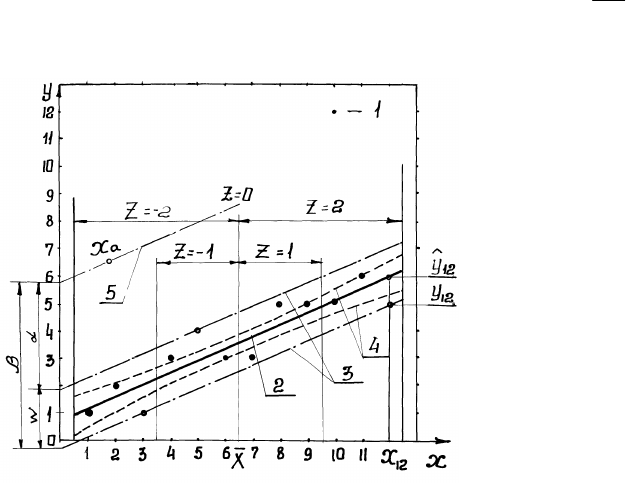
Рис. 7. Построение доверительного интервала для истинной линии регрессии (ИФР) в

предположении о её линейном характере:

1 - результаты измерений; 2 – аналитическая линия регрессии (АЛР); 3 - вспомогательные

прямые, параллельные АЛР, для определения размаха W

невязок (остатков); 4 - верхняя и

нижняя границы 95%-ного доверительного интервала для ИФР, построенная быстрым методом; 5 -

вспомогательная прямая, параллельная АЛР, для определения выброса невязок (остатков) с

помощью табл. 1; точка Х

- выброс.

(Рекомендуется точки с Рис. 7 перенести на миллиметровку, размножить и раздать

учащимся; для идентификации и исключения выброса Х

- воспользоваться критериями из табл.1;

результат выполнения на миллиметровке упражнения 1 можно сверить с построениями на рис. 7).

Проверка гипотез

Чтобы избегать ошибок, надо набираться опыта; чтобы набираться опыта,

надо делать ошибки. (Принцип компетентности по Питеру)

При линейном однофакторном регрессионном анализе тезис простоты (см. введение)

можно проиллюстрировать следующим образом. Если опыты не противоречат предположению об

отсутствии регрессии Y на X, то полученная регрессия (точнее, оценка в

коэффициента

)

незначима. Так, например в пределах доверительного интервала на рис. 6 можно изобразить

горизонтальную прямую 4 (y

= 2). Значит, на уровне значимости

= 0,05 регрессия Y по X в

этом случае незначима (если абстрагироваться от физического смысла величин Y и X).

С другой стороны, если у нас имеются априорные содержательные (рациональные или

теоретические) представления об исследуемом объекте, то наиболее простым будет объяснение

зависимости с позиций априорных содержательных представлений. В примере 14 из

рациональных соображений можно предположить, что остаточная концентрация взвеси Y

отсутствует, когда нет нагрузки X при осветлении сточных вод после очистки газа. В этом случае

ИФР может иметь вид

X. Поэтому в примере 12 наиболее простой оценкой регрессии X по Y

является

= 0,64x (см. линию 5 на рис. 6).

При обработке данных методом скользящей средней мы использовали только одно

предположение - о гладкости функции регрессии (6.2). В линейном регрессионном анализе мы

пользуемся более сильным предположением - о линейном характере функции (6.2) и получаем

более узкий ДИ для ИФР.

Упражнение 2. Необходимо по данным из упражнения 1 (см. рис. 8) быстро построить ЭФР

в предположении о гладкости ИФР модифицированным методом скользящей средней и построить

83-% - ный доверительный интервал для ИФР (рекомендуется точки с Рис. 7 также перенести на

миллиметровку, размножить и раздать учащимся; результат выполнения на миллиметровке

упражнения 2 можно сверить с построениями на Рис. 8).

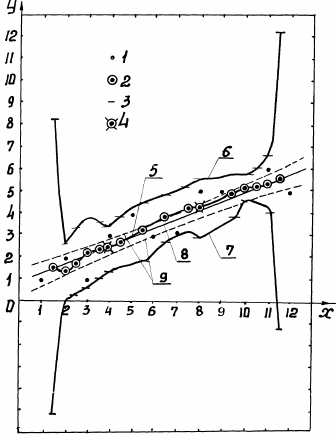
Рис. 8. Сравнение доверительных интервалов для ИФР, построенных в предположении о

монотонном характере ИФР (6.2) методом скользящей средней и в предположении о линейном

характере ИФР по формуле (6.14):

1 - результаты измерений; 2 - скользящие средние; 3 - границы 83%-ных доверительных интервалов

около скользящих средних 2; 4 - точки начала и конца значимой регрессии; 5 – эмпирическая линия

регрессии; 6, 7 - верхняя и нижняя граница 83%-ного доверительного интервала для ИФР, построенная по

методу скользящей средней с помощью программы ММСС [14]; 8 - аналитическая линия регрессии (график

линейной эмпирической функции регрессии); 9 – 95%-ный доверительный интервал, построенный по

формуле (6.14)

Пример 15. Из рис. 8 видно, что предположение (6.8) о самом простом - линейном

характере функции (6.2) приводит к более узкому доверительному интервал для ИФР. Однако по-

прежнему ИФР может быть любая линия, лежащая в пределах этого нового доверительного

"коридора". Так, в пределах доверительного интервала для ИФР на рис. 8 можно провести

экспоненту, параболу, синусоиду, кусочно-линейную или ступенчатую линию. Все они могут

незначимо отличаться от прямолинейной регрессии, но требуют содержательного обоснования.

Экстраполяция.

Чем туманней прогноз, тем проще ему сбыться. (Из интернета)

Тот минимум предположений, который принимается для построения ДИ методом

скользящей средней, не позволяет

экстраполировать ЭЛР за пределы области её определения

между минимальным и максимальным выборочными значениями }{max}{min

xxx

≤

: ДИ

для ИФР расширяется до бесконечности (см. рис. 1, 4 и 8). Однако, если у исследователя есть

основание предполагать, что некая функция регрессии (6.2) Y по X справедлива и за пределами

изученной области, то построенный ДИ (например, по уравнениям (6.14) - (6.17)) позволяет

экстраполировать ЭФР. Разумеется, с увеличением расстояния от изученной области ДИ для

ИФР расширяется, ошибка предсказания значений ИФР растет (см. рис. 4, 6 - 8).

Линейная однофакторная регрессия с одним коэффициентом

Есть только один способ покончить с навязчивыми мыслями, -

додумать их до конца. Андрей Коряковцев

Формальное применение статистических методов без содержательного анализа

результатов расчёта может привести к неверным статистическим моделям. Простым примером

формального подхода является промежуточный результат решения учебного примера 12 (см.

рис. 6): нижняя граница ДИ для линейной ИФР

X заходит в область физически

недопустимых значений при y < 0. В данном случае природе описываемого явления больше

соответствует линейная модель регрессии с одним коэффициентом

Y = βx + ε

, ε

~ N(0,σ

), (6.22)

где Y – отклик,

- коэффициент регрессии, x – фактор,

– СО отклика Y.

Подобные модели нередко встречаются на практике [2, 7, 14, 24].

Пусть в результате измерения значений y

отклика Y при фиксированных значениях x

фактора X получена выборка {x

}; i = N,1 . Она позволяет найти эффективные однозначные

оценки параметров

линейной регрессионной модели (6.22) [18]:

(

)

(

)

iii

bxyx

∑∑

; (6.23)

()()

0,5

ˆˆ

YYii

SyyNσ



==−−





∑

, (6.24)

где

- значение отклика Y в точке x

, вычисленное с помощью ЭФР

= bx; (6.25)

- остаточное СО отклика Y.

Вместо непосредственного расчёта S

по формуле (6.24) проще использовать выражение

()

0,5

222

Yii

SybxN





=−−









∑∑

. (6.26)

Интервальная оценка ИФР (6.14) определяется значением полуразмаха ДИ (6.15), где

сомножитель Ф зависит от значения величин x,

и N так:

Ф = Ф

(Z, α, N) = x t

f;α /2

(

)

0,5

−

∑

; (6.27)

f;α /2

- число Стьюдента с числом степеней свободы f = N – 1 (см. [рис. 4Р1]).

Поскольку функция (6.22), где величина Ф определяется выражением (6.27), является

уравнением прямой, проходящей через начало координат, то для её построения достаточно

вычислить лишь ещё одно значение полуразмаха

∆

при любом значении x .

Удобно выбирать x =

, где n - целое число (например, x = 10

=1, или 10

=10 и т. п.).

Пример 16. Предполагается, что зависимость Y от X по данным примера 12 описывается

линейной регрессионной моделью (6.22).

Найти эффективные однозначные оценки параметров этой модели и построить

интервальную оценку линейной регрессии Y по X с доверительной вероятностью 1 -

= 0,95.

Решение. Воспользовавшись формулами (6.23) и (6.25), получаем b = 35/55 = 0,636, то есть

= 0,636x (рис. 9); по формуле (6.26) S

= [(24 - 0,636

⋅55)/4]

0,5

= 0,66. Проверим последний

результат непосредственно по формуле (6.24) S

= [(0,4

+ 0,75

+0,9

+ 0,45

+ 0,15

)/4]

0,5

= 0,66.

Построим интервальную оценку прямолинейной регрессии (6.22). По [рис. 4Р1] находим

4;0,05/2

= 2,8; по формуле (6.27) Ф = Ф

(Z, α, N) = 5⋅2,8⋅55

-0,5

= 1,89 при х = 5; по формуле (6.15)

∆

= 1,89⋅0,66 = 1,25 при х = 5. Восстанавливаем перпендикуляр к оси X в точке х = 5 (см. рис. 9);

от точки пересечения этого перпендикуляра с ЭФР откладываем вверх и вниз значения

полуразмаха ∆

= 1,25; соединяя полученные точки прямой линией с началом координат, строим

верхнюю и нижнюю границы ДИ с доверительной вероятностью 1 -

= 0,95.

Ответ. ЭФР имеет вид y

= 0,66x (см. линию 2 на рис. 9); СО остаточной ошибки S

= 0,66;

границы 95%-ного ДИ также изображены на рис. 9.

Рис. 9. Регрессия остаточной концентрации взвеси в осветленной воде по удельной нагрузке

гидроциклона-флокулятора (окончательный результат обработки данных примера 12):

обозначения Y и Х см. на рис. 8; 1 - результаты измерений; 2 – график ЭФР y

= 0,636x; 3, 4 – границы

95%-ного доверительного интервала, построенные эффективным и быстрым методами, соответственно;

и w

- максимальная и минимальная невязки, соответственно;

∆

– полуразмахи ДИ, построенные

быстрым и эффективным (при х = 5) методами, соответственно; экстраполяция в область x > 5

допустима, а в область x < 0 (штриховка) лишена физического смысла.

Быстрое оценивание линейной регрессии с одним коэффициентом

Объявление: «Быстро и качественно сделаем любую халтуру» (из интернета)

Для однозначного оценивания линейной регрессии (6.22) также воспользуемся методом

«натянутой нити». Только прямая линия должна проходить точно через начало координат, а

экспериментальные точки равномерно располагаться по обе стороны от линии [20].

Коэффициент b = Y/X, где X – значение фактора; Y – соответствующее значение отклика на

прямой. Удобно выбирать X = 10

, где п целое число. Получим ЭФР

= b х.

Быструю оценку остаточного СО отклика вычислим по формуле

= w

N-1

. (6.28)

Для интервального оценивания ИФР

(х) =

х находим размах невязок W

по формуле

(6.18); нижнюю

и верхнюю

границы определяем по формуле (6.14), а полуразмах ДИ –

по формуле

(

)

0,5

б YNi

WKxx

−

∆=

∑

, (6.29)

где К

N-1

в зависимости от значений α и N-1 находим в табл. 2. Сумму квадратов

∑

можно

вычислить непосредственно или, при большом объёме выборки N, выразив через среднее

СО S

∑

() ()

NNSNx



=−+



, (6.30)

заменить в формуле (6.30) эффективные оценки быстрыми (

- медианой

, СО S

– оценкой

′

, вычисляемой по формуле (5.1)), получим быструю оценку суммы квадратов

∑

()()

NSx



′



. (6.31)

Другую быструю оценку суммы квадратов

∑

без расчёта медианы

выведем так.

Дополним выборку значений фактора {x

} (i =

N,1

) симметричной выборкой {-x

} (i =

N,1

Приравняем эффективную оценку СО величины Х, S

хэ

= [2

∑

/(2N-1)]

0,5

, полученную по

суммарной выборке {-x

, x

} (i =

1,2

), быстрой оценке S'

хэ

= 2х

, где х

max{}

максимальная варианта в выборке. Получим (

∑

)

0,5

= (4N-2)

0,5

. Теперь формула

(6.29) примет вид

()

0,5

012

б YNNm

WKxaNx

−

∆=−. (6.32)

Значение полуразмаха ДИ при х = х

вычисляется совсем просто:

()

0,5

012

ббmYNN

WKaN

−

∆=∆=−. (6.33)

Пример 17. По данным примера 14 получить быстрые однозначную и интервальную (с

доверительной вероятностью 1 -

= 0,95) оценки линейной регрессии (6.22) и СО отклика.

Решение. Методом натянутой нити строим быструю оценку линии регрессии (она почти

совпадает с линией 2 на рис. 9). По формуле (6.18) определяем W

= 0,8 + 0,9 = 1,7; по формуле

(6.28) S'

= 1,7/2,06 = 0,83; по формуле (6.31);

∑

≈

()

(

)

54/2,33359;

+= формуле (6.29)

∆

= 1,7

⋅

0,72

⋅

5/(59)

0,5

= 0,80. Похожий результат получим и по формуле (6.33):

бm

∆

= 1,7

⋅

0,72

⋅

3,08/(4

⋅

5-2)

0,5

= 0,89. Восстановим перпендикуляр в точке х =5 к оси Х (см. рис.

9); от точки пересечения этого перпендикуляра с ЭФР откладываем вверх и вниз значение

полуразмаха

∆

; проведя через полученные точки и начало координат две прямые, получим

верхнюю и нижнюю границы (3) ДИ.

3.7. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ

Ах, только бы тройка не сбилась бы с круга, бубенчик не смолк под дугой,

две верных подруги - любовь и разлука - не ходят одна без другой. Булат Окуджава.

Иногда исследователю необходимо только проверить, имеется ли между двумя величинами

Y и X линейная связь, определить её направление и тесноту [29]. Количественной мерой тесноты и

направления линейной связи между двумя величинами является коэффициент корреляции

определенный на области от - 1 до 1. Близость

нулю свидетельствует о слабой (или об

отсутствии - при

= 0) линейной связи; близость

к | 1 | - о тесной связи; при

= - 1 или

1 имеется, соответственно, отрицательная, или положительная функциональная линейная связь Y с

X. Знак перед

указывает на направление этой связи: если

> 0, положительная связь

проявляется в том, что при увеличении значений X значения Y «в среднем» возрастают;

отрицательная связь (

< 0), когда при увеличении значений X значения Y «в среднем» убывают.

Эффективная оценка коэффициента корреляции [16]:

(

)

(

)

(

)

5,0

111

























−













−−==

∑∑∑∑∑∑∑

=======

yyNxxNyxyxNrρ . (7.1)

Пример 17. По данным условий и таблицы решения примера 14 вычислить эффективную

оценку коэффициента корреляции между величинами Y и X.

Решение. По формуле (7.1): r = (5*35-15*10)/{[5*55-15

]*[5*24-10

]}

0,5

= 0,79.

Быстрый графический метод оценивания коэффициента корреляции

Между горлом и ногами существует тесная связь: промочишь ноги -

заболит горло, промочишь горло - заплетаются ноги. (Из интернета)

Излагаемый ниже метод имеет максимальную эффективность среди быстрых методов

оценивания коэффициента корреляции

[4, 10]. Метод сводится к следующим действиям.

Исходные данные, представленные выборкой {x

}; i =

N,1

где x

- значения фактора X

; y

значения отклика Y, наносятся на график в координатах Y-X; методом натянутой нити [20] наносят

прямую, аппроксимирующую экспериментальные данные; оценивают размах отклика W

разность между максимальным и минимальным его значениями:

{

}

{

}

yy minmax

−

; (7.2)

по формуле (6.18) вычисляют размах невязок W

и, наконец, быструю оценку коэффициента

корреляции

(

)

[

]

(

)

5,0

1sgn

WWbr −=

′

, (7.3)

где b

- коэффициент ЭФР (6.12), или тангенс угла наклона прямой к оси 0Х; знак [sgn(b

)] перед

коэффициентом b

элементарно определяется «на глаз» (само значение коэффициента b

здесь не

используется!). Формула (7.3) легко получается из известного соотношения [1]

()

(

)

0,5

sgn1

YXY

ρβσσ=−



, (7.4)

где

- дисперсии отклика - условная и общая. Заменяя

на

′

;

- их

быстрыми оценками (6.21) и (5.1), соответственно, и, принимая а

/а

N-2

≈ 1 (для N > 3), приходим к

формуле (7.3).

Пример 19. По данным примеров 12 и 14 вычислить быструю оценку коэффициента

корреляции между Y и X. Решение выполняем по формуле (7.3): r' = [+](1-1,5

/(3-1)

)

0,5

= 0,66.

Проверка гипотез относительно коэффициента корреляции

Что не докажем, то предположим. (Авессалом Подводный)