Цейтлин Н.А. Из опыта аналитического статистика
Подождите немного. Документ загружается.


4
факторов. Разумно предположить, что некоторые факторы в количестве k (1 ≤ k ≤ n) можно не
измерять для вычисления Y. Тогда дисперсия
2
Y
σ
вычисления Y должна возрасти на некую
величину
2
u
σ
. Практически величина
2
u
σ
может быть ничтожно мала по сравнению с дисперсией
2
Y
σ
, обусловленной погрешностями измерения всех факторов. Это предположение может быть
сформулировано в виде гипотезы Н
Т
против Н
Э
(1).
Отметим, что задача элиминирующего анализа лишь внешне похожа на задачу определения
ничтожной погрешности косвенного измерения (см. выше [Р4.2]), но отличается от неё
принципиально: это - разные задачи.
4.4. Рациональное табулирование функции
Многие задачи научных и инженерных расчетов завершаются построением таблицы
сложной для расчёта функции (например, формулы косвенных изменений, эмпирической функции
регрессии или сложной математической модели объекта, программно реализованной на ЭВМ).
Значения выходной величины по этой таблице находят путём интерполирования (обычно
линейного) с допустимой погрешностью.
Пусть имеется адекватная некоторому объекту табулируемая функция (ТФ)
(
)
Yfx
= (где
Y - выходная величина;
x
- n-мерный вектор входных переменных). ТФ предназначена для
построения соответствующей таблицы. На действующем физическом объекте измерены значения
факторов
, 1,
i
xin
= с некоторыми случайными
погрешностя
ми λ
i
~
(
)
2
0,
i
N
σ
. С помощью
таблицы по результатам измерений входных переменных
i
x
необходимо
будет
определять
значения выходной величины Y с дисперсией
2
Y
σ
погрешност
и, обусловленной дисперсиями
2
i
σ
погрешностей
измерения входных переменных
i
x
а также дисперсией
погрешност
и самой ТФ.
Дисперсия погрешности таблицы будет складываться из дисперсии погрешности округления
табличных значений выходной переменной Y и погрешности интерполяции. От этого дисперсия
2
Y
σ
должна возрасти на некую величину
2
u
σ
.
Задача рационального табулирования функции заключается в выборе таких шагов
табулирования входных переменных
, 1,
i
xin
= и такого округления численных значений
выходной переменной Y, чтобы определяемая этими факторами дисперсия
2
u
σ
погрешности
таблицы была ничтожно мала по сравнению с «естественной» дисперсией
2
Y
σ
погрешности
выходной переменной. Это утверждение может быть сформулировано в виде гипотезы Н
Т
против
Н
Э
(1).
4.5. Установление адекватности простых математических моделей в составе сложных
[Р6.4.3.].
Простая математическая модель (ПММ, например, математическая модель параметров
физико-химических свойств) бывает вложеной в сложную математическую модель (СММ,
например, в математическую модель химико-технологической системы) и адекватна ей тогда,
когда составляющая
2
u
σ
дисперсии отклика СММ, обусловленная погрешностями расчета
параметров ПММ, составляет величину ничтожно малую по сравнению с составляющей
дисперсией отклика
2
Y
σ
СММ, обусловленной погрешностями определения факторов всей
СММ. Этому утверждению соответствует статистическая гипотеза Н
Т
против Н
Э
(1).
Сформулированные гипотезы позволили решить две задачи [5]: прямую - проверить
адекватность «простой» математической модели физико-химических свойств «сложной»
математической модели химико-технологической системы и обратную - определить требования к
максимальному пределу погрешности математической модели физико-химических свойств,
удовлетворяющему условию адекватности математической модели химико-технологической
системы. Так, например, анализ уравнения баланса массы и теплоты в теплообменнике
дистилляции содового производства показал, что уравнение для расчета теплоемкости со СО
случайной ошибки 40 Дж/(кг
⋅
К), используемое в примере, адекватно уравнению баланса (решена

5
прямая задача); это уравнение будет адекватно, пока СО погрешности расчета теплоемкости не
превысит 90 Дж/(кг
⋅
К) (решена обратная задача).
4.6. Оценка дисперсии воспроизводимости опыта в регрессионном анализе по данным
«пассивного» эксперимента [6; Р6.2.2.]
Дисперсию воспроизводимости опыта (ДВО)
2
bY
σ
оценивают обычно по результатам
параллельных наблюдений [2]. Однако в «пассивном» эксперименте вероятность получения
строго параллельных наблюдений ничтожно мала. В работе [6] предложено получать смещенную
(завышенную) и несостоятельную оценку
2
bY
S
ДВО
2
bY
σ
с помощью ряда пар «почти»
параллельных опытов в многофакторном эксперименте.
Воспользуемся следующей итерационной процедурой. По результатам N наблюдений
построим обычную оценку регрессионной функции
ˆ
Y
(x) в первом приближении (x – n-мерный
вектор факторов). С помощью этой функции сформулируем требование «почти» параллельности
для любых пар точек x
i
и x
j
как гипотезу о том, что квадрат приращения оценки функции отклика
()
(
)
2
2
ˆˆ
uij
YxYxσ
=−
в точках x
i
и x
j
ничтожно мал по сравнению с остаточной дисперсией
2
Y
σ
регрессионной модели. Это условие можно сформулировать в виде гипотезы Н
Т
против Н
Э
(1).
Вычисляем уровень значимости
ˆ
α
для q таких гипотез. Мера
(
)
()
()
1
1,
ˆ
,max
n
ijirjrlr
r
lN
LxxxxYxx
=
∈
=−∂∂
∑
, (7)
характеризующая «расстояние» между «почти» параллельными опытами в точках x
i
и x
j
должна
удовлетворять условию
(
)
,
iju
Lxx
σ
<
. Далее наблюденные в экспериментах значения отклика Y
i
,
Y
j
используют для оценки
2
bY
S
ДВО
2
bY
σ
. Это позволяет проверять адекватность регрессионной
модели обычным путём, сравнивая ДВО с остаточной дисперсией. Если модель адекватна,
расчеты останавливают, если – нет, переходят к следующей итерации: подбирают более сложную
регрессионную функцию и т. д.
Ключевая идея рассмотренного метода заключается в следующем. Если окажется, что
полученная на некоторой итерации регрессионная функция не адекватна, когда оценка
2
bY
σ
является смещенной, то, очевидно, что при несмещенной оценке
2
bY
σ
эта же модель будет
тем более не адекватна!
Таким образом, сконструирован критерий не адекватности регрессионной функции,
построенной по данным «пассивных» наблюдений.
4.7. Округление численных оценок параметров регрессионной модели [Р6.2.5]
Пусть по известным матрице плана
X
размерностью (
Nk
×
) и вектору откликов
(
)
12
,,...,
N
YYYY
= методом наименьших квадратов получены «точные» неокругленные численные
оценки b
i
коэффициентов β
i
(
1,
im
= ) эмпирической функции регрессии (ЭФР)
(
)
ˆ
ˆ
,
Yfxb
= (в
большинстве программ ЭВМ для записи чисел b
i
используется от 6-ти до 9-ти цифр). Если
округлить численные оценки b
i
коэффициентов ЭФР, то нормальная остаточная ошибка
Е ~ N(ν
,
2
Y
σ
) (с центром ν = 0 и дисперсией
2
Y
σ
> 0) с неокругленными коэффициентами b
i
может
превратиться в худшую ошибку Е
0
~ N(ν
0,
σ
0
2
) с округленными коэффициентами b
i0
: возрастает
остаточная дисперсия (
σ
0
2
>
2
Y
σ
); появится систематическая составляющая ошибки (
ν
0
≠
0). Это
позволяет сформулировать одну пару гипотез относительно центра распределения ошибки Е
Н
10
: ν
0
= 0; Н
11
: ν
0
≠ 0. Для формулировки второй пары гипотез относительно дисперсии величины
Е будем считать, что приращение
2
u
σ
дисперсии
2
Y
σ
пренебрежимо мало по сравнению с
дисперсией
2
Y
σ
. Аналогично предыдущему опять приходим к гипотезам Н
Т
против Н
Э
(1).
В настоящее время все семь перечисленных выше задач нуждаются в соответствующем
современным требованиям программном обеспечении.
6
Литература
1. Цейтлин Н. А. Применение методов математической теории эксперимента в содовой
промышленности // Обзорн. инф. Серия «Содовая пром-сть». - M.: НИИТЭХИМ, 1984. -36 с.
2. Цейтлин H. А. Определение верхнего допустимого предела случайной погрешности измерения
технологического параметра при планировании эксперимента // Методы математической статистики в
основной химии: Труды. T. 55 / НИОХИМ. - Харьков, 1981. - С. 167 - 176.
3. Вознесенский В. А. Статистические методы планирования эксперимента в технико-экономических
исследованиях. - M.: Статистка, 1981. - 264 с.
4. Цейтлин Н. А. Элиминирующий анализ детермированных математических моделей химико-
технологических систем // В кн.: Процессы и аппараты производств основной химии: Труды НИОХИМа. –
Т. 56. - Харьков, 1981. - С. 29 – 38.
5. Цейтлин Н. А. Адекватность регрессионных моделей физико-химических свойств растворов
математическим моделям химико-технологических систем. Журн. Прикл. Химии № 11, 1983, с. 2520-2525.
6. Цейтлин Н. А., Гордеев Д. С., Ицков Ф. Э., Рудай А. Н. Оценка дисперсии воспроизводимости
отклика в пассивном регрессионном эксперименте. - Теор. осн. хим. технолог, т. 21, № 6, с.830-835, 1987.
7. Браунли К. А. Статистическая теория и методология в науке и технике. - М.: Наука, 1977. - 408 с.
8. Головач А. В., Ерина А. M., Трофимов В. П. Критерии математической статистики в экономических
исследованиях. – M.: Статистика, 1973. - 135 с.
9. Смирнов H. В., Дунин-Барковский И. В. Курс теории вероятностей и математической статистики для
технических приложений. – M.: Наука, 1965. - 511 с.
10. Айвазян С. А., Енюков И. С., Мешалкин Л. Д. Прикладная статистика: Основы моделирования и
первичная обработка данных. - M.: Финансы и статистика, 1983. - 472 с.
11. Айвазян С. А., Енюков И. С., Мешалкин Л. Д. Прикладная статистика: Исследование зависимостей:
Справ. изд. - M.: Финансы и статистика, 1985. - 487 с.
1
5. Элиминирующий анализ
Говорят, что числа правят миром. Нет, они только показывают, как правят миром.
Иоганн Вольфганг Гёте
В настоящем разделе приведено описание сравнительно нового направления в
математической статистике, получившего название «элиминирующий анализ»; описаны
основные положения этого направления, иллюстрируется его высокая эффективность при
исследовании сложной математической модели с факторами, имеющими недиагональную
корреляционную матрицу, описаны аналитический и численный методы элиминирования
факторов и алгоритм программы для ЭВМ, приведены примеры расчётов.
Элиминирующий анализ имеет большое прикладное значение, так как позволяет
существенно сократить необоснованно громоздкую математическую модель (технологического
процесса, формулу косвенного измерения физических параметров и т. п.) за счет незначимых
факторов и способствует углублению представлений о роли значимых факторов в
математической модели.
Современные методы математического моделирования становятся столь совершенными, а
уровень знаний столь высоким, что сложная математическая модель (СММ), создаваемая со
знанием природы явления - с минимальным числом упрощающих допущений, делается
необозримо большой и громоздкой [11]. СММ может включать в себя ряд малосущественных
факторов или
простых математических моделей
(ПММ), описывающих существенные сами по
себе явления. Практическая проверка СММ на описываемом ею физическом объекте может
показать, что многие малосущественные факторы или ПММ практически не «работают».
Наличие неработающих компонентов СММ создает ненужную иллюзию «полного знания», хотя
на самом деле практически значимой роли не играют. В описанной иллюзии не было бы большой
беды, если бы, к примеру, программно реализованные неработающие ПММ просто
паразитировали где-то в недрах ЭВМ. Однако часто при использовании СММ на практике для
управления процессами, обеспечения технологических и проектных расчетов бывает необходимо
измерять независимые переменные СММ - факторы. Подобные измерения могут быть
продолжительными и дорогостоящими. Кроме того, на создание СММ и их реализацию в ЭВМ
тратится много сил, времени и средств, которые на поверку оказываются напрасными.
Основной задачей элиминирующего анализа является редукция (сокращение) СММ.
Этим она принципиально отличается от задачи построения новой математической модели с
использованием результатов наблюдений (например, методом регрессионного анализа).
Задачи элиминирующего анализа близки к задачам планирования отсеивающего
эксперимента [Р12.7]. Однако эксперимент связан с активным воздействием на объект
исследования, а в элиминирующем анализе рассматриваются результаты «пассивных»
наблюдений за работой реального объекта: оцениваются параметры распределения факторов, а
затем в СММ объекта специальным образом выделяются незначимые факторы.
Многие задачи построения математической модели завершаются построением
эмпирического полинома.
В элиминирующем анализе структура СММ сохраняется
: в
упрощенной СММ незначимые факторы заменяются их постоянными (например, средними)
значениями. Это важное отличие способствует сохранению адекватности СММ и её основных
аппроксимирующих свойств.
В каком случае более целесообразно получить упрощённую СММ, а в каком – просто
полином, - зависит от конкретных условий задачи.
Нa одном из этапов элиминирующего анализа происходит ранжирование факторов по силе
их влияния на отклик. Эта информация может быть использована как для свертки СММ, так и для
содержательного анализа процесса и управления им.
В приложении задача элиминирующем анализе возникает, например, при замене на
предприятиях устаревшего оборудования и аппаратов новыми, при использовании формул
косвенного измерения в управлении производственными процессами, в системах автоматического
регулирования и в других подобных случаях.
Пример 1. Смена поколений.
Химическое предприятие обычно включает сотни различных
аппаратов, связанных материальными и энергетическими потоками. Один из путей

2
совершенствования химического производства заключается в замене старых морально и
физически устаревших аппаратов новыми. Новые аппараты подключают в действующую сеть так,
что многие материальные потоки сохраняют прежние значения.
Для расчета характеристик новых аппаратов используют довольно сложные математические
модели, включающие десятки и сотни формул [11]. Это – формулы расчета параметров
физических свойств газов и жидкостей, газо-паро-жидкостного равновесия, структуры потока
жидкостей, химических реакций, массообмена и многие другие. Одни формулы являются
эмпирическими регрессионными функциями, другие – аналитической записью законов природы.
Достоинством подобных моделей является возможность учета практически всех факторов
процесса. Однако эти модели не лишены недостатков. Разработка подобных моделей занимает
многие годы, сложность моделей затрудняет их реализацию на ЭВМ, проверку адекватности и
интерпретацию результатов расчета. Часто оказывается, что многие формулы, входящие в состав
математической модели аппарата, просто «не работают» ввиду малого интервала варьирования
учитываемых в них переменных или значимой корреляции между ними. Как упростить эти
модели? Необходимо провести исследование «старого» химического аппарата в режиме
нормальной эксплуатации, измерить факторы, определяющие изучаемый процесс, а отклики
(характеристики) нового проектируемого аппарата рассчитать с помощью СММ. Полученные
данные позволят существенно упростить СММ путем элиминирования незначимых факторов.
Особую актуальность задача редукции СММ приобретает при объединении математических
моделей отдельных аппаратов в одну гигантскую математическую модель всего производства.
5.1. Элиминирующий анализ формулы косвенного измерения
Далее будут описаны постановка и решение статистической задачи элиминирующего
анализа, рассмотрены два метода её решения – аналитический и численный - для анализа и
редукции СММ с малым и большим числом факторов, соответственно.
5.1.1. Постановка задачи элиминирующего анализа.
Введём некоторые аббревиатуры, обозначения и определения:
ЛПР - лицо, принимающее решение;
ЛПРТ - ЛПР, стремящееся добиться высокой точности измерений (ЛПР «точное»);
ЛПРЭ - ЛПР, стремящееся к экономии средств (ЛПР «экономное»);
CO - среднеквадратичное отклонение; выборочные СО S
x
и дисперсия
2
x
S - это
статистические оценки генеральных СО σ
x
и дисперсии
2
x
σ
величины х, или в краткой записи:
S
x
→
σ
x
и
2
x
S
→
2
x
σ ;
x = (x
1
x
2
… x
n
)
Т
– n-мерный вектор факторов;
n,1
= 1, 2, …, n;
H
0
, H
1
- нулевая и альтернативная гипотезы;
измерение - нахождение значения физической величины опытным путем с помощью
специальных методов и технических средств;
прямым является измерение, при котором искомое значение величины (фактора х)
находят непосредственно из опытных данных;
фактором х называется прямо измеряемая физическая переменная величина,
характеризующая действующий физический объект, принимающая в некоторый момент времени
определенное значение;
косвенным является измерение, при котором искомое значение величины (отклика Y)
находят на основании известной зависимости между этой величиной и величинами,
подвергаемыми прямым измерениям – вектором факторов x;
откликом Y называется косвенно измеряемая физическая переменная величина,
характеризующая физический объект, принимающая в некоторый момент времени определенное
рассчитанное значение;
ФКИ - формула косвенного измерения - известная функциональная зависимость отклика Y
от вектора факторов x:
Y = f (θ, x), (1)

3
где f(θ, x) - известная (обычно – гладкая) функция; θ ∈ R
m
- вектор известных значений
коэффициентов; x
∈
Q
⊂
R
n
- вектор факторов - многомерная случайная величина, определённая на
области действия Q.
Измерение на реальном объекте факторов, входящих в ФКИ, может быть трудоемким,
длительным, дорогим. Параметры распределения факторов, наблюдаемых на объекте, могут быть
таковыми, что некоторые из них можно элиминировать, заменив их значения в ФКИ константами
(например, средними значениями). Элиминируется такое подмножество множества факторов,
которое не дает значимого роста погрешности косвенного измерения. Процедуры оценивания
статистических параметров и проверки гипотез, связанные с элиминированием факторов,
названы элиминирующим анализом.
Одной из главных задач элиминирующего анализа является идентификация
элиминируемых факторов.
Пусть погрешности λ
i
прямого измерения факторов x
i
случайны, нормально распределены и
независимы, λ
i
~ N(0,
2
i
λ
σ ), i =
n,1
. Вместо истинных значений факторов x
i
на объекте наблюдаются
их приближенные значения Х
i
= x
i
+ λ
i
[3].
В каждом опыте вектор факторов x рассматривается как детерминированная величина,
элементы которого x
i
прямо измеряются со случайными независимыми погрешностями. С другой
стороны, в процессе функционирования физического объекта вектор факторов x принимает
различные значения и поэтому
может рассматриваться как случайный
.
Параметры распределения случайных величин x и λ обычно представляют выборочными
оценками. Так, экспериментальное тарирование приборов, предназначенных для прямого
измерения на объекте величин x
i
, i =
n,1
, фиксированных на некоторых уровнях, позволяет
получить оценки
2
i
S
λ
дисперсий
2
i
λ
σ погрешностей измерения фиксированных факторов с
i
f
λ
степенями свободы.
Отметим, что погрешность λ
i
прямого измерения фактора x
i
обусловлена не только
случайной погрешностью собственно метода измерения, но и нестабильностью самого фактора x
i
,
фиксированного на заданном уровне, из-за турбулентных пульсаций, броуновского движения,
вибрации и многих других подобных причин.
Путем N-кратного измерения значений x на физическом объекте получают оценки
параметров распределения x: векторы средних
x
x
µ
→
, дисперсий
22
xx
S σ→
с f = N - 1
степенями свободы и корреляционную матрицу ||r
ij
|| → || ρ
ij
||.
Предполагается, что дисперсии
2
i
λ
σ пренебрежимо малы в сравнении с соответствующими
дисперсиями
2
i
x
σ
[Ф(1)Р4].
Случайная погрешность вычисленного по ФКИ (1) значения отклика
Y
~
, обусловленная
погрешностями измерения величин x
i
, имеет оценку дисперсии
222
||
1
n
Y
И iYИ
i
SE
σ
=
≈→
∑
(2)
с числом степеней свободы, определяемым по формуле Вэлча [4]
44
||
1
(/)
i
n
Y И Y И i
i
fSEf
λ
=
=
∑
. (3)
Величины
i
SXYE
xii λ
|)/(
∂
∂
=
(4)
и
2
i
E
являются соответственно CO и дисперсией частной погрешности косвенного измерения
отклика, обусловленной погрешностью прямого измерения фактора x
i
. Производные
i
XY
∂
∂
/
берутся, вообще говоря, при значениях факторов x
i
, фиксированных на некоторых (например, на
средних) уровнях,
T
n
xxxx ),...,,(
21
=
.
Если число факторов n - велико, то, используя ФКИ (1) при вычислении Y для реального
объекта, нам необходимо выполнять чрезмерно большое число (n) измерений значений факторов.
Можно предположить, что некоторые факторы x
1
, x
2
,…, x
k
в количестве k (1 ≤ k ≤ n) можно
элиминировать, то есть не измерять для вычисления Y.
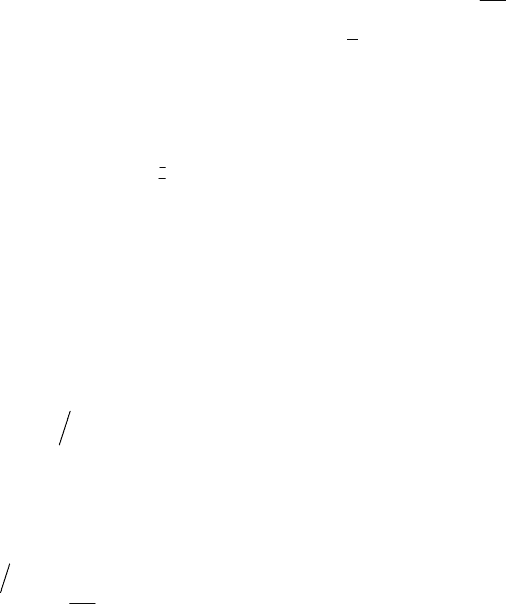
4
Замечание. В данной постановке вопрос об измерении значений отклика Y не ставится. Во-
первых, значения отклика Y могут быть получены расчетным путём; во-вторых, часто это сделать
вообще невозможно. Например, основной показатель содового производства – выход бикарбоната
натрия из карбонизационной колонны измерить почти невозможно [2]). Измерение значений
отклика (когда это возможно) можно использовать (см., пример из физхимии [Р6.4.4]) для
проверки адекватности СММ или ФКИ, или уточнения моделей. Но это уже другая задача.
5.1.2. Принципы решения задачи элиминирующего анализа.
Предположим для простоты, что множество Ω = (x
1
, x
2
, …, x
k
) первых k факторов x
i
(
ki ,1=
,
1 ≤ k ≤ n) ФКИ можно элиминировать путем замены их средними значениями
i
x . Это приводит к
увеличению дисперсии отклика
2
Y
σ
на величину
2
|ΩY
σ , оценка которой
2
|
11
kk
Yijij
ij
SWWr
Ω
==
=
∑∑
; (5)
i
xxii
SXYW |)/( ∂∂=
, (6)
где W
i
и
2
i
W являются соответственно CO и дисперсией частной погрешности отклика,
обусловленной элиминированием фактора x
i
,
с числом степеней свободы f
= N – 1.
Если k факторов элиминируют, значит, их не измеряют. Тогда вклад погрешности измерения
оставшихся n - k факторов в дисперсию
2
Y
σ
отклика будет меньше, и оцениваться дисперсией
2
|Y
И
S
Ω
с числом степеней свободы f
Y|ИΩ
, вычисляемыми соответственно по формулам (2) и (3), в
которых суммирование начинается не с i = 1, а с i = n – k:
222
||
n - k
n
Y
И iYИ
i
SEσ
ΩΩ
=
≈→
∑
(7)
44
||
n - k
(/)
i
n
Y И Y И i
i
fSEf
λ
ΩΩ
=
=
∑
. (8)
Теперь дисперсия
2
Y
σ
отклика Y, или её оценка
2
Y
S
определятся суммами
222
||YYY
И
σσσ
ΩΩ
=+
или
222
||YYY
И
SSS
ΩΩ
=+
, (9)
а число степеней свободы f
Y
дисперсии
2
Y
S
определится формулой Вэлча [4] в виде
444
||
(//)
YYYYИИ
fSSfSf
ΩΩΩ
=+
. (10)
Для того чтобы первые k факторов x
i
(
ki ,1=
, 1 ≤ k ≤ n) ФКИ могли быть элиминированы,
слагаемое
2
|ΩY
σ
в формуле (9) должно быть ничтожно малым по сравнению с дисперсией
2
|ИY
σ
.
Возникает следующая задача: до какого верхнего допустимого предела можно увеличивать
составляющую
2
|ΩY
σ дисперсии погрешности отклика, обусловленную элиминированием k
факторов, чтобы она по сравнению с
2
|ИY
σ оставалась ничтожно малой?
Эта задача сформулирована в виде гипотез Н
Т
против Н
Э
и решена выше [Р4].
Принципы работы вычислительного алгоритма элиминирующего анализа.
Расчет CO частных погрешностей косвенного измерения отклика, обусловленных
погрешностями прямого измерения (E
i
), или элиминирования (W
i
) факторов x
i
в ФКИ по формулам
(4), или (6), соответственно, страдает тремя недостатками. Во-первых, многократное
вычисление частных производных трудоёмко; во-вторых, ФКИ (1), как правило, нелинейная и
поэтому расчеты по формулам (4) и (6) неточные, а погрешности расчетов не определены; в
третьих
, использование коэффициентов парной корреляции r
ij
в формуле (5) предполагает
наличие лишь линейной корреляции между факторами, которая на самом деле может быть и
нелинейной. Допускаемые при этом погрешности расчета также не определены. Перечисленных
недостатков лишен излагаемый ниже численный алгоритм элиминирующего анализа.
Реализация этого метода на ЭВМ облегчается наличием готовых подпрограмм в большинстве
пакетов программ статистического анализа: ввода и преобразования матрицы данных, поиска
информативных признаков, оптимизации, расчета средних, дисперсий, корреляций и т. д.
5
Замечание. Как видно из формулы (5), при положительных значениях коэффициентов
парной корреляции r
ij
между факторами x
i
и x
j
(r
ij
> 0) CО погрешности (W
i
) косвенного измерения
отклика, обусловленная элиминированием фактора x
i
, возрастает, а при отрицательных значениях
r
ij
(r
ij
< 0 ) – убывает.
5.1.3. Численный алгоритм элиминирующего анализа
Исходные данные: ФКИ (1); матрица (x
ij
) ( Ni ,1= строк; nj ,1= столбцов) результатов
наблюдений факторов и вектор (S
иj
) (
nj ,1=
элементов) CO погрешностей прямых измерений
факторов. Предполагается, что ФКИ (1) на малых интервалах
(X
i1
, X
i2
, …, X
ij
, …, X
in
), (X
i1
, X
i2
, …, X
ij
+ S
иj
, …, X
in
), (
nj ,1=
) (11)
приближенно линейная (рис. 1).
Рис. 1. Иллюстрация к расчёту по формулам (12) и (13):
S
иj
- СО погрешности прямого измерения фактора x
j
;
и
ij
∆ - i-тая численная оценка СО частной погрешности косвенного измерения
отклика, обусловленная СО S
иj
погрешности прямого измерения фактора x
j
( nj ,1= ,
Ni ,1= ).
Тогда величина E
j
вычисляется как СО приращения отклика
и
ij
∆ = f(θ, X
i1
, X
i2
, …, X
ij
, …, X
in
) – f(θ, X
i1
, …, X
ij
+ S
иj
, …, X
in
), (12)
обусловленного приращением соответствующего фактора х
i
(см. схему расчета в табл.1 и рис. 1) в
каждой точке
Ni ,1=
на интервале (12):
()
(
)
0,5
2
и
1
N
jij
i
EN
=
=∆
∑
. (13)
Разности
0
ии
iijij
YY −=∆ (табл. 1) точно равны величинам E
j
в окрестности точки х
i
в случае,
когда ФКИ (1) линейная и приближенно равны E
j
, когда - нелинейная. Поэтому для расчета
величин E
j
по линейной ФКИ (1) достаточно выполнить только один цикл расчета (i = 1).
Вычисленные значения отклика Y
i0
в точках х
ij
следует хранить в памяти ЭВМ для
дальнейшего использования.
Таблица 1.
Схема расчета среднеквадратичных отклонений E
j
по формуле (12).
Задать Вычислить
(и направить в сумматор)
i j X
i1
X
i2
X
i3
Y
ij
(
)
2
и
1i
∆
(
)
2
и
2i
∆
(
)
2
и
3i
∆
1 0 X
11
X
12
X
13
Y
10
1 X
11
+ S
и1
X
12
X
13
Y
11
(
и
11
Y
- Y
10
)
2
2 X
11
X
12
+ S
и2
X
13
Y
12
(
и
12
Y
- Y
10
)
2
3 X
11
X
12
X
13
+ S
и3
Y
13
(
и
13
Y - Y
10
)
2
2 0 X
21
X
22
X
23
Y
20
6
1 X
21
+ S
и1
X
22
X
23
Y
21
(
и
21
Y
- Y
20
)
2
2 X
21
X
22
+ S
и2
X
23
Y
22
(
и
22
Y
- Y
20
)
2
3 X
21
X
22
X
23
+ S
и3
Y
23
(
и
23
Y - Y
20
)
2
… … …. … …. … …. …. …
N 0 X
N1
X
N2
X
N3
Y
N0
1 X
N1
+ S
и1
X
N2
X
N3
Y
N1
(
и
1N
Y
- Y
N0
)
2
2 X
N1
X
N2
+ S
и2
X
N3
Y
N2
(
и
2N
Y - Y
N0
)
2
3 X
N1
X
N2
X
N3
+ S
и3
Y
N3
(
и
3N
Y - Y
N0
)
2
Здесь i - номер опыта (
Ni ,1=
); j - номер фактора (
nj ,1=
); n = 3.
Численный метод расчета величины S
Y|Ω
- CO составляющей погрешности отклика,
обусловленной множество Ω элиминируемых факторов в ФКИ (1).
Исходные данные: ФКИ (1) и матрица (X
ij
) ( Ni ,1= , nj ,1= ) результатов наблюдений
факторов. Искомую величину CO
()
()
0,5
2
/
1
1
N
Yi
i
SN
ΩΩΩ
=
=∆−∆−
∑
(14)
определим по приращениям (рис. 2) отклика Y
∆
i
Ω
= f(θ, X
i1
, …, X
ik
, …, X
ij
, …, X
in
) – f(θ,
1
X
, …,
k
X , …, X
ij
,…, X
in
), (15)
где
Ω
∆ - систематическая составляющая погрешности отклика, обусловленной
элиминированием множества
Ω
факторов, равная
1
N
i
i
N
ΩΩ
=
∆=∆
∑
. (16)
Величина
Ω
∆
является оценкой точного значения
ν
Ω
систематической составляющей
погрешности отклика. Предполагается, что
ν
Ω
= 0, а величина
Ω
∆
случайно колеблется вокруг
этого значения. Однако слишком большое значение величины
Ω
∆ может говорить о том, что
ν
Ω
≠
0. Для проверки гипотезы H
0
:
ν
Ω
= 0 против Н
1
:
ν
Ω
≠
0 используется
α
-критерий Стьюдента [1,
c. 8] (см. также гипотезу 1 [Т3Р1]).
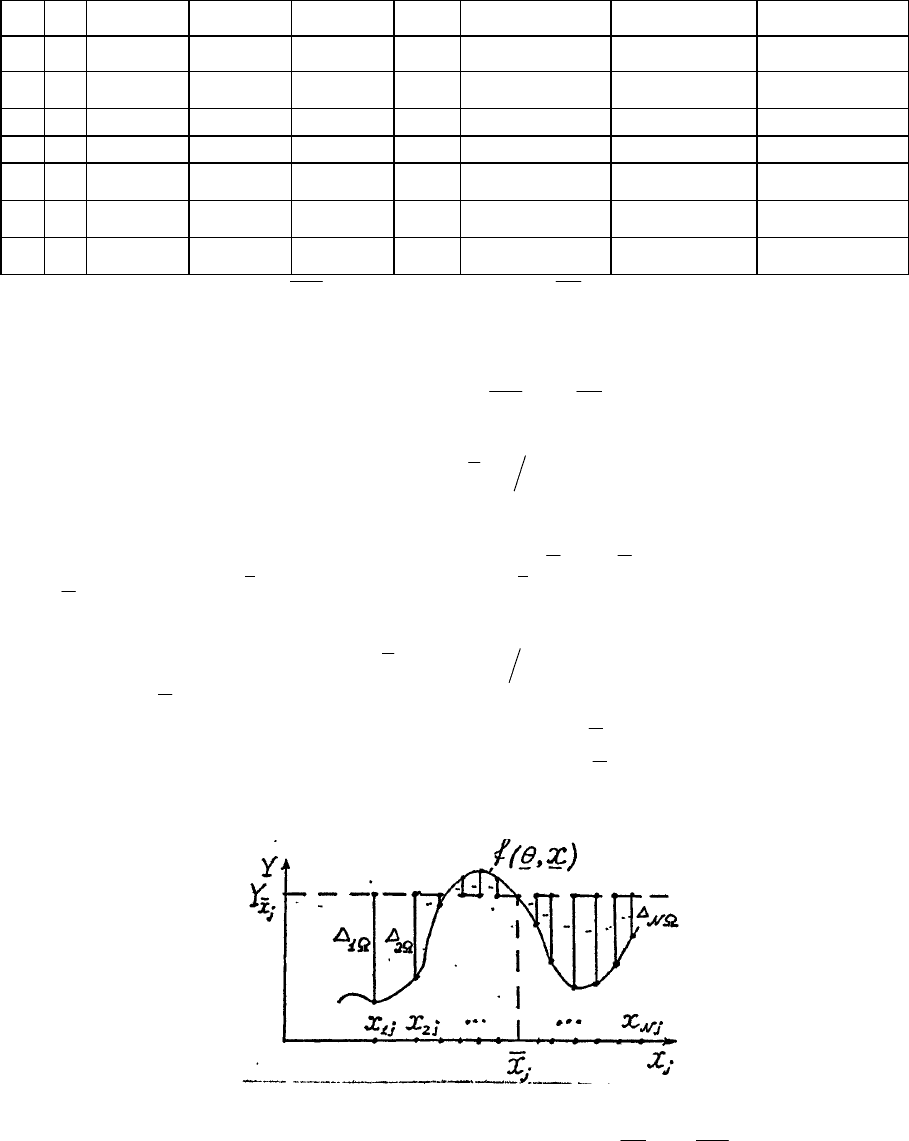
Рис. 2. Иллюстрация к расчёту по формулам (14) и (15):
∆
i
Ω
- i-тая численная оценка частной погрешности косвенного измерения отклика,
обусловленная элиминированием фактора x
i
( nj ,1= , Ni ,1= ).
Для этого ЛПР априори задают критические значения
α
к
уровня значимости. Причём ЛПРТ
задаёт значение
α
кт0
, руководствуясь предпочтением гипотезы
Н
0
(см. [Т2Р1]), а ЛПРЭ задаёт
α
кЭ1
, руководствуясь предпочтением гипотезы Н
1
.
Затем вычисляется статистика
t
α
ˆ
критерия
Стьюдента [1, c. 12] по формулам

7
()
()
0,5
0,5
222
0,5
/
ˆ
11exp0,6118;22;
21,5;/.
t
Y
ZZLLtN
LNttNS
α
ΩΩ
=−−−=−−+
=++=∆
(17)
Если окажется, что
t
α
ˆ
>
α
к
, то ЛПР гипотезу H
0
не отклоняют; если же
t
α
ˆ
<
α
к
, то –
отклоняют.
В последнем случае, который изредка может встречаться, необходимо изменить координаты
вектора k элиминируемых факторов, то есть элиминировать эти факторы не путём замены их в
ФКИ средними значениями
12
,,
xx
…,
k
x
, а заменить их такими другими значениями, которые
приведут ЛПР к отклонению гипотезы H
0
:
ν
Ω
= 0. Это - задача оптимизации функции цели
Ω
∆ →
0
в пространстве Ω ⊂ Q.
5.1.4. Идентификация множества элиминируемых факторов ФКИ
Выше для удобства записи суммы от 1 до k в формуле (5) предположили, что множество Ω
элиминируемых в ФКИ (1) факторов включает первые k факторов (1 ≤ k ≤ n).
На самом деле идентификация множества
Ω
элиминируемых факторов является проблемой,
известной как «задача выбора информативной подсистемы признаков» [9, с. 71].
Информативными в нашем случае являются факторы, остающиеся в ФКИ (1) после
элиминирования не информативного подмножества
Ω
факторов.
Формально задача ставится так (9, с. 72). Пусть дана исходная система признаков X = {X
1
,
X
2
, …, X
n
}. Необходимо указать наиболее информативную с точки зрения некоторого критерия γ
подсистему, состоящую из m признаков (m < n).
Рассмотрим некоторую подсистему
{
}
12
,,...,
m
XXX
ννν
, 1 ≤ ν
1
≤ ν
2
≤ … ≤ ν
m
≤ n. Введем
n-мерный булев вектор U = (U
1
, U
2
, …, U
n
). Рассматриваемой подсистеме ставим в соответствие
значение вектора U = (U
1
, U
2
, …, U
n
) так, что U
j
= 1, если X входит в эту подсистему, либо U
j
= 0,
если X
j
не входит в неё.
Таким образом задача выбора наиболее информативной подсистемы признаков ставится как
экстремальная задача на единичном гиперкубe. В качестве допустимой области D выступает
подмножество вершин гиперкуба, число которых равно
m
n
C ; функция γ(п) является
многоэкстремальной; её значения в различных точках определяются алгоритмическим путем.
Среди большого числа методов, определяющих порядок перебора вершин указанного
гиперкуба [5, 6, 9] можно выделить методы включения и исключения [5], используемые для
определения значимых факторов в регрессионном анализе. Один из этих методов применяется в
зависимости от того, каких признаков ожидается больше: если ожидается, что информативных
признаков большинство, используется метод исключения из ФКИ не информативных признаков
(табл. 2); если не информативных признаков большинство, используется метод включения в ФКИ
информативных признаков.
Таблица 2.
Последовательность перебора элиминируемых факторов методом исключения из ФКИ (1).
Вычислить
Задать
отклик приращение (26)
i j X
i1
X
i2
X
i3
Y
ij
Y
ij
-Y
i0
1 1
1
X
X
12
Х
13
Y
11
Y
11
-Y
10
2 1
1
X
X
22
Х
23
Y
21
Y
21
-Y
10
…………………………………………………………………………………………………….
N 1
1
X
Х
N2
Х
N3
Y
N1
Y
N1
-Y
N0
…………………………………………………………………………………………………….
1 2 Х
11
2
X
Х
13
Y
12
Y
12
-Y
10
2 2 Х
21
2
X
Х
23
Y
22
Y
22
-Y
20
…………………………………………………………………………………………………….
