Цейтлин Н.А. Из опыта аналитического статистика
Подождите немного. Документ загружается.

6
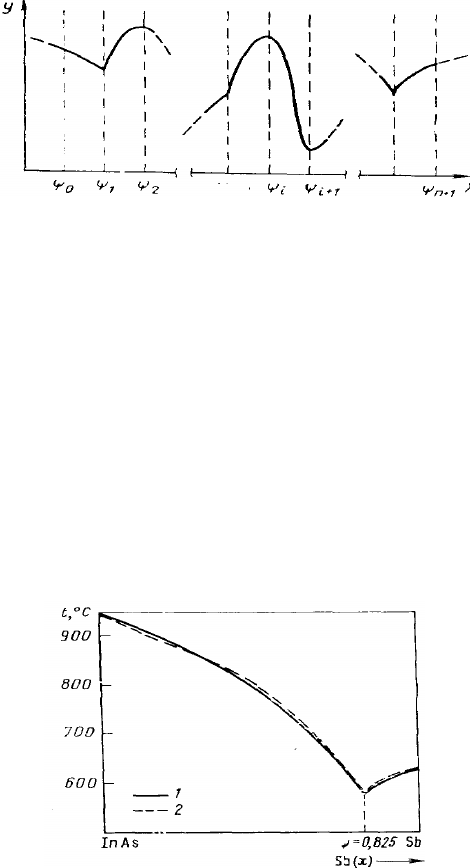
Рис. 4. Гладкая непрерывная функция с разрывами первого рода непрерывности её первой
производной
Рассмотрим
несколько решений
.
ПЕРВОЕ решение заключается в объединении функций f
j
(x) для отдельных гладких
участков с помощью индикаторных функций П(
ψ
j
-1
,
ψ
j
, x), то есть в построении модели
()
()
(
]
1
101
1
,,,,
n
jjjn
j
yfxП xxψψψψ
+
−+
=
=∈
∑
, (24)
где j - номер гладкого участка; п + 1 - их число;
ψ
j
- абсцисса излома.
Разрывами непрерывности функции (24) в точках
ψ
j
приходится пренебрегать.
Пример 3. В работе [16] методом дифференциально-термического анализа (ДТА)
определены температуры ликвидус сплавов системы InAs - Sb, представляющей собой диаграмму
эвтектического типа практически без растворимости компонентов в твердом состоянии. Ставится
задача построить для этой диаграммы аппроксимацию кривой ликвидус (рис. 5).
Рис. 5. Ликвидус системы InAs - Sb: 1 - по данным работы [16]; 2 - по аппроксимации (25)
Авторы работы [16] установили концентрацию сурьмы в эвтектической точке
ψ
= 0,825
долей единицы по массе, а также определили эвтектическую температуру. По этим данным мы
рассчитали дисперсию ошибки воспроизводимости опыта в определении температур (у):
2
y
S =
14.6 с числом степеней свободы f = 7. Методом наименьших квадратов для каждого гладкого
участка линии ликвидуса построили полиномиальные функции регрессии, а затем в соответствии
с выражением (24) объединили их с помощью индикаторных функций (1). В результате получили
следующую эмпирическую функцию регрессии (ЭФР), аппроксимирующую кривую ликвидус
системы InAs - Sb (см. рис. 5):
у = (942 – 246x + 72,4x
2
– 372x
3
)П(0; 0,825; х) + (3663х - 1187 - 1845х
2
)П(0,825; 1; х), (25)
где y - температура ликвидус, °С; х - концентрация Sb, доли единицы (по массе).
На участке х
∈
(0; 0,825] ЭФР (25) имеет остаточную дисперсию 7,49 (f = 7); на участке х
∈
(0,825; 1] - дисперсию 16,09 (f = 3). Сравнение этих дисперсий с указанной выше дисперсией
ошибки воспроизводимости свидетельствует об адекватности модели (25).
ВТОРОЕ решение рассматриваемой задачи заключается в том, что функцию, показанную
на рис. 4, предлагается аппроксимировать комбинацией функций
7
()()
()()()()
011
1
1
11111,010,1
1
,,,,,,,,.
n
ii
i
n
jjjjjnnn
j
yxx
Dx
П xJxIxJxIx
βββψ
ψψψψψψψψ
+
=
−
++
=
=++−+
+++
∑
∑
(26)
В этом выражении первые три члена представляют собой кусочно-линейную
аппроксимацию (19); П(
ψ
j
,
ψ
j+
1
, x) - индикаторная функция (1); I
1,0
(
ψ
1
, х) и I
0,1
(
ψ
n
, x ) - единичные
ступенчатые функции (4) и (5); D
j
(
ψ
j
,
ψ
j+
1
, х) - кривые, закрепленные в точках (
ψ
j
, 0) и (
ψ
j+
1
, 0)
так, как показано, на рис. 6, а, то есть
D
j
(
ψ
j
,
ψ
j+
1
,
ψ
j
) = D
j
(
ψ
j
,
ψ
j+
1
,
ψ
j+
1
) = 0,
1,1 −= nj
; (27)
J
1
(
ψ
1
, x) и J
n
(
ψ
n
, x) - кривые, закрепленные в точках (
ψ
1
, 0) и (
ψ
n
, 0) так, как показано на рис. 6, б,
то есть
J
1
(
ψ
1
,
ψ
1
) = J
n
(
ψ
n
,
ψ
n
) = 0. (28)
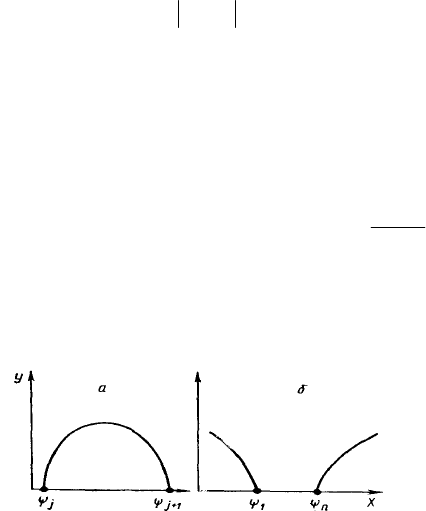
Рис. 6. Графики кривых: a – D(
ψ
j
,
ψ
j+
1
, x); б – J
1
(
ψ
1
, x) и J
n
(
ψ
n
, x)
Таким образом, функция (26) состоит из кусочно-линейной функции типа (19), являющейся
как бы каркасом, сложенной с кривыми D(*) и J(*), проведенными с учетом ограничений (27) и
(28) и помноженными соответственно на индикаторные П(*) и ступенчатые I(*) функции.
Кривую D
j
(
ψ
j
,
ψ
j+
1
, х) можно аппроксимировать параболой k-того порядка (k
≥
2):
(
)
1
0
,,
k
i
kjjjji
i
Dxx
ψψβ
+
=
=
∑
. (29)
С учетом ограничения (27) получим
(
)
(
)
12
111
1211
200
,,,2
kii
iississ
kjjjjijjjj
iss
Dxxxkψψβψψψψ
−−
−−−−+
+−++
===
=−+≥
∑∑∑
. (30)
В некоторых простых случаях D
j
(
ψ
j
,
ψ
j+
1
, х) можно аппроксимировать полуволной синусоиды
(
)
(
)
(
)
[
]
jjjDjjsj
xxD
j
ψ
ψ
ψ
π
β
ψ
ψ
−
−
=
++ 11
/sin,,
; (31)
функцией эллиптического вида
(
)
(
)
(
)
0,5
2
1111
,,2/
j
ejjjDjjjjjj
Dxxx
ψψβψψψψψψ
++++
=+−−−
; (32)
параболой второго порядка
(
)
(
)
[
]
(
)
[
]
4//,,
2
1111
2
12 +++++
+−−+−=
jjjjjjjjDjjj
xxxD
j
ψψψψψψψψβψψ . (33)
Коэффициент
j
D
β
в выражениях (31) - (33) определяется значением величины у при
х = (
ψ
j
+
ψ
j+
1
) /2, то есть
j
D
β
= D
j
(
ψ
j
,
ψ
j+
1
, (
ψ
j
+
ψ
j+
1
) /2). (34)
Кривые J
j
(
ψ
j
, x) при j = 1 или п в функции (26) с учетом ограничений (28) можно
аппроксимировать полиномами k-того порядка:
(
)
(
)
1
,,1
k
ii
kjjjij
i
Jxxjn
ψβψ
=
=−=∪
∑
. (35)

8
ТРЕТИЙ способ аппроксимации кривой, показанной на рис. 4, предполагает
использование функции
(
)
(
)
1101
0
,,,,,(,]
n
jjjjjn
j
yCxПxxψψψψψψ
+++
=
=∈
∑
, (36)
где П(
ψ
j
,
ψ
j+
1
, х) - индикаторная функция (1); C
j
(
ψ
j
,
ψ
j+
1
, х) - кривая, закрепленная в точках
(
)
j
y
j ψ
ψ
,
и
(
)
1
,
1
+
+
j
y
j ψ
ψ
, то есть
(
)
(
)
1
111
,, и ,,
+
=
=
+++
jj
yСyC
jjjjjjjj ψψ
ψ
ψ
ψ
ψ
ψ
ψ
. (37)
Функции C
j
(
ψ
j
,
ψ
j+
1
, х) представляют собой уравнения гладких участков, которые
«сшиваются» с помощью условий
C
j
(
ψ
j
,
ψ
j+
1
, х) = C
j+
1
(
ψ
j+
1
,
ψ
j+
2
, х) при х =
ψ
j+
1
,
1,0 −= nj
. (38)
С учетом ограничений (37) кривую C
j
(
ψ
j
,
ψ
j+
1
, х) можно аппроксимировать параболой k-того
порядка
(
)
(
)
(
)
1
111
,,()/(),,
jj
j
kjjjjjjkjjj
CxyyyxDx
ψψ
ψ
ψψψψψψψ
+
+++
=+−−−+
, (39)
где D
kj
(
ψ
j
,
ψ
j+
1
, х) определяется функцией (30).
При k = 1 значение D
1
j
(
ψ
j
,
ψ
j+
1
, х) = 0, a
(
)
(
)
(
)
[
]
(
)
111
/,,
1
++
−
−
−
+
=
+
jjjjjj
xyyyxC
jjj
ψ
ψ
ψ
ψ
ψ
ψψψ
. (40)
При k
≥
2, как следует из функций (39) и (30),
(
)
11
2
,,
k
kjjsjjj
s
CCDx
ψψ
+
=
=+
∑
. (41)
Например, при k = 2
C
2
j
= C
1
j
+ D
2
j
= C
1
j
+
β
0
j
[x
2
– x (
ψ
j
+
ψ
j+
1
) +
ψ
j
ψ
j+
1
]; (42)
при k = 3
(
)
[
]
2
11
22
11
23
1213213 ++++
++++−++=++=
jjjjjjjjjjjjjjj
xxDCDDCC ψψψψψψψψβ . (43)
Наконец, в некоторых случаях кусочно-гладкие функции (рис. 4) можно аппроксимировать
суммой полиномов k-того порядка и кусочно-линейных функций типа (19) с п изломами:
01
kkn
i
ijjk
ijk
yxxββψ
+
−
==+
=+−
∑∑
. (44)
Функции (24), (26), (36) и (44) в отличие от форм, рассматриваемых в статье [8], линейны по
параметрам, что облегчает оценивание последних (в случае, когда значения
(
)
nj
j
,1=ψ заданы) с
помощью обычных методов линейного регрессионного анализа [18]. Число параметров
β
ji
и
ψ
j
этих функций для каждого гладкого участка (
ψ
j
,
ψ
j+
1
) кусочно-гладкой функции отклика (см. рис.
4) не должно превышать числа экспериментальных точек на этих участках.
Для программирования на ЭВМ функция (44) удобнее других. Если значения абсцисс точек
изломов
ψ
j
не известны, их можно оценить наряду с параметрами
β
ji
методами нелинейного
регрессионного анализа [6, 18]. Вычисление параметров
β
ji
без ЭВМ быстро осуществляется с
помощью формул (22) и (31) - (34).
(Внимательный читатель, наверно, давно заметил, что символы W, D, C, J, I и П для
обозначения аппроксимирующих функций мы подбирали специально так, чтобы они были похожи
на графики этих функций J. Остальные обозначения, естественно, общепринятые).
Пример 4. В работе [17] методом ДТА построена диаграмма состояний системы индий -
сурьма с устойчивым химическим соединением InSb и двумя эвтектиками в частных системах In -
InSb и InSb – Sb (рис. 7).
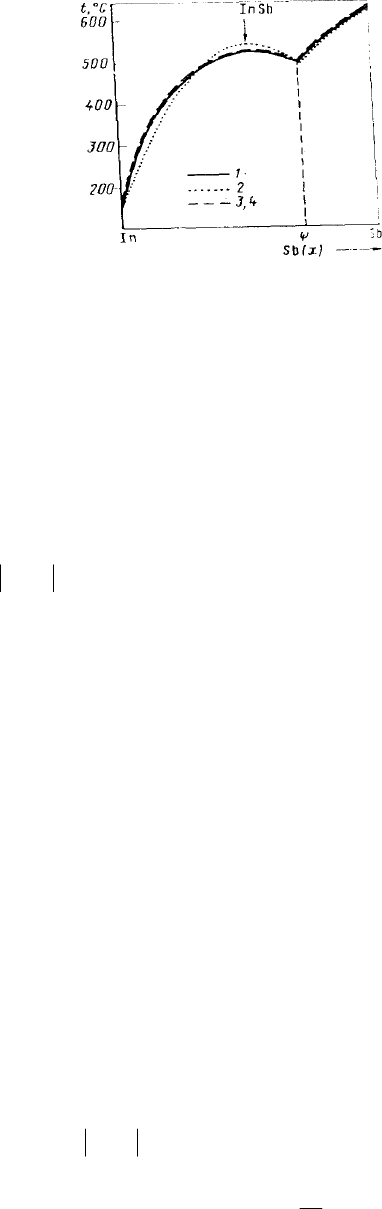
9
Рис. 7. Ликвидус системы In – Sb, построенный: 1 - по данным работы [17]; 2-4 - по ЭФР
соответственно (49), (51), (53).
Кривая ликвидус этой диаграммы состоит из двух гладких участков, имеющих излом в
точке кристаллизации двойной эвтектики в системе InSb - Sb. Многократные определения [17]
показали, что концентрация Sb в эвтектической точке
ψ
= 0,71 долей единиц (по массе), а
эвтектическая температура у
ψ
= 493
о
С. Рассчитанная по результатам параллельных опытов
дисперсия ошибки воспроизводимости опыта в определении температуры
2
y
S = 0,77
(среднеквадратичное отклонение (СО) S
y
= 0,88 °С) с числом степеней свободы f
1
= 10.
Для аппроксимации кривой ликвидус системы In - Sb вначале воспользуемся обработкой
данных без ЭВМ. Искомая аппроксимация, в соответствии с (26), имеет вид
(
)
(
)
(
)
(
)
xIxDxIxDxbxbby ,
ˆ
,1,
ˆ
,
ˆ
,
ˆ
,0
ˆ
1,020,11210
ψψψψψ ++−++=
. (45)
Предположим, что в данном случае точки (х
1
, у
1
), (
ψ
, у
ψ
) и (х
N
, у
N
) лежат на одной прямой
(см. рис. 7). Тогда кусочно-линейная часть ЭФР (45) примет вид
Ф(x) = 156,4 + 474,lx. (46)
При х =
ψ
ˆ
= 0,71 получим
ψ
ˆ
y = 156,4 + 474,1
⋅
0,71 = 493
o
С. Следовательно, опыты не
противоречат сделанному предположению.
Аппроксимируем функции D
1
(0,
ψ
, x) и D
2
(
ψ
, 1, x) из уравнения (45) параболами второго
порядка (33). Для этого проведем две прямые линии через точки (х
1
, у
1
), (
ψ
, у
ψ
) и (
ψ
, у
ψ
), (х
N
, у
N
).
Разделим прямые пополам и, в соответствии с выражением (34), определим величины
j
D
β
.
Получим
1
D
β
= 173,
2
D
β
= 12. По формуле (33) определим
D
1
(0,
ψ
,x) = -1372(x
2
- 0,71х), (47)
D
2
(ψ, 1, x) = -570(x
2
– 1,71x + 0,71). (48)
Таким образом получена аппроксимация кривой ликвидус системы In - Sb (см. рис. 7)
y = 156,4 + 474,1x + [-1372(x
2
– 0,71x)]I
1,0
(0,71; x) + [-570(x
2
– 1,71x + 0,71)]I
0,1
(0,71; x). (49)
Формула (49) предсказывает температуру ликвидус плохо, хотя нельзя не отметить, что в
правой части кривой (см. рис. 7) совпадение расчетных и экспериментальных значений кажется
удовлетворительным.
Перейдем теперь к аппроксимации кривой ликвидус функцией
(
)
(
)
(
)
(
)
xIxJxIxJxbxbby ,
ˆ
,
ˆ
,
ˆ
,
ˆˆ
1,010,10210
ψψψψψ ++−++=
, (50)
которая, как и функция (45), следует из выражения (26).
Коэффициенты уравнений (35) для J
j
(
ψ
; х),
1,0=j
подбирали методом линейного
регрессионного анализа (на ЭВМ "Наири-2"). Значимость оценок коэффициентов определяли по t-
критериям Стьюдента при критическом уровне значимости
α
= 0,05 [18].
Расчет коэффициентов b
ji
уравнения (50) сопровождали уточнением положения
эвтектической точки
ψ
в системе In Sb - Sb. В некотором интервале изменяли координату этой
10
точки, каждый раз определяя при этом все коэффициенты ЭФР (50) и СО S
ост
остаточной ошибки.
Зависимость СО S
ост
от положения точки
ψ
показана на рис. 8 (кривая 1).
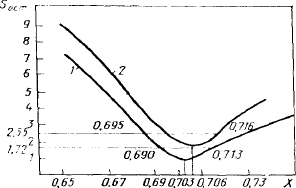
Рис. 8. Зависимость среднеквадратичного отклонения остаточной ошибки S
ост
от положения точки
х =
ψ
для модели: 1 - типа (50), 2 - типа (44)
Оказалось, что минимум СО S
ост
остаточной ошибки наблюдается при
ψ
ˆ
= 0,703. В результате
была получена ЭФР для кривой ликвидус системы In - Sb (см. рис. 7)
у = 5959 – 6777x - 525|х - 0,703 | + [8668(х - 0,703) - 9107(x
2
– 0,703
2
) + 26583(х
3
– 0,703
3
) –
- 45337(х
4
- 0,703
4
) + 41621(х
5
- 0.703
5
) - 15373(х
6
- 0,703
6
)]I
1,0
(0,703; х) + [8524(х - 0,703) -
- 450 (х
2
– 0,703
2
)]I
0,1
(0,703; х). (51)
Остаточная дисперсия для этой ЭФР
2
ост
S = 0,97 с числом степеней свободы f
2
= N - m = 25 -
11 = 14, где N - число опытов; m - число коэффициентов ЭФР (51). Расчетное значение F-критерия
F
ˆ
= 0,97/0,77 = 1,26 меньше табличного при 5%-ном уровне значимости (F
0,05;14;10
=
2,86).
Следовательно, гипотеза об адекватности ЭФР (51) не отвергается.
Построим интервальную оценку для координаты эвтектической точки
ψ
, воспользовавшись
уравнением [18]:
(
)
0,5
1
;;
1()
остост mNm
SSmNmF
αα
−
−
=+−
, (52)
где S
ост
α
- приближенное значение для контура остаточной ошибки с уровнем значимости
α
. В
данном случае S
ост
=
0,985; F
0,05;11;14
= 2,60, поэтому S
ост
α
= 1,72. Точки пересечения изолинии
S
ост
= 1,72 с кривой 1 на рис. 8 определяют доверительные интервалы для
ψ
с уровнем значимости
0,05. Таким образом, как следует из рис. 8, с вероятностью 0,95 концентрация сурьмы в
эвтектической точке
ψ
системы InSb - Sb лежит в интервале между 0,690 и 0,713 долей единицы
Sb (по массе). Отметим, что определенная экспериментально в работе [17] эта точка
ψ
= 0,71
лежит внутри полученного интервала, ближе к его верхней границе.
Еще одна аппроксимация кривой ликвидус системы In - Sb была получена с помощью
функции (44). Степень полинома, дающего минимальное СО S
ост
, вновь искали методом
линейного регрессионного анализа, причем, как и в предыдущем случае, этот поиск сопровождали
уточнением положения эвтектической точки
ψ
в системе InSb - Sb.
В данном случае минимум СО S
ост
наблюдается при
ψ
= 0,706 (рис. 8, кривая 2), что
незначимо отличается от величины
ψ
= 0,703, определенной выше.
В результате была получена ЭФР для кривой ликвидус системы In - Sb (рис. 7)
у = -216 + 2696х - 5754х
2
+ 9331х
3
- 8630х
4
+ 3049х
5
+ 530 |х - 0,706|. (53)
Для этой ЭФР остаточная дисперсия
2
ост
S = 3,24 при f
2
= 25 - 7 = 18. Расчетное значение F-
критерия
F
ˆ
= 3,24/0,77 = 4,21 и в этом случае меньше табличного, но при
α
= 0,01
(F
0,01;18;10
= 4,47). Гипотеза об адекватности ЭФР (53) не отвергается.
Интервальную оценку концентрации Sb в эвтектической точке
ψ
определили так же, как и в
предыдущем случае. Здесь S
ост
= 1,80; F
0,05;7;18
= 2,59, поэтому по формуле (52) S
ост
α
= 2,55. Из рис.
8 следует, что в данном случае 95 %-ная интервальная оценка концентрации точки
ψ
есть (0,695;
0,717) долей единицы Sb (по массе).
11
Метод кусочно-постоянной аппроксимации В. Ф. Пастушенко и Х. Шиндлера
В. Ф. Пастушенко и Х. Шиндлер [20] предложили численный алгоритм построения
кусочно-постоянной аппроксимирующей сплайн - функции (в приложении к задаче обнаружения
уровней напряжения в ионном канале).
Математическое ожидание (МО) отклика имеет небольшое количество К неизвестных
уровней и в течении эксперимента М раз перескакивает от одного из К значений к другому.
Опыты сопровождаются белым шумом с неизвестной дисперсией. Числа замеров N и скачков М
обычно велики (N > 10000 и М > 1000).
Целью метода является установление К значений уровня МО и узлов сплайн - функции
(моментов времени, в которые МО перескакивает от одного из К значений к другому). Метод
включает
два этапа
.
На первом этапе последовательность данных подвергается кусочно-постоянной
фильтрации с целью обнаружения скачков МО в узлах сплайн - функции. Текущие значения МО
оцениваются как средние величины У.
i
в сгруппированных данных. Для сравнения пар соседних
МО используется статистический критерий (Стьюдента или Гаусса). Для формирования первой
группы точек из временного ряда берутся три первые точки, и вычисляется среднее значение
отклика. Затем проверяется гипотеза Н
0
о принадлежности следующей 4-й точки к первой группе.
Если эта гипотеза не отклоняется, 4-я точка включается в первую группу, опять вычисляется
среднее значение отклика и вновь проверяется гипотеза Н
0
о принадлежности 5-й точки к первой
группе. И так далее. Цикл повторяется до того момента, когда гипотеза Н
0
отклоняется. Вторая
группа точек составляется аналогично первой. Таким фильтром проходят весь ряд из N точек и
выделяют М групп точек с различными (обычно в точности не совпадающими) средними
значениями отклика У.
м
(м = 1, 2, ..., M) в каждой группе.
На втором этапе М групп точек собирают в К статистических ансамблей. Для определения
числа К используется следующий остроумный приём. М групп точек выстраивают в
вариационный ряд по значениям величин У.
м
так, что У.
i
≤
У
i+1
(i = 1, 2, ..., M-1) (индексы м
заменяются на соответствующие i). На графике прорисовывается неубывающая функция
времени, ПОХОЖАЯ на кусочно-постоянную аппроксимацию с явно видными почти
горизонтальными участками. Число этих участков принимается равным К. Вычисляют средние
взвешенные значения У..
i
(i = 1, 2, ..., К) из средних У.
i
в каждом ансамбле. При сравнении пар
У..
i
и У..
j
(i, j = 1, 2, ..., К; i < j) оценок МО для ансамблей вновь используется статистический
критерий. Метод подвергнут тестированию с использованием имитируемых данных.
Таким образом, метод сводится к оценке параметров
ψ
j
, β
j
(j = 1, 2, ..., M) и
σ
2
регрессионной модели
(
)
1
1
,,
K
jjj
j
yx
βψψε
−
=
=Π+
∑
, (54)
где П(a, b, x) – индикаторная функция (1);
ε
- случайная нормально распределённая ошибка с
центром в нуле и дисперсией
σ
2
, а параметры β
j
принимают всего К значений (К << М).
Особенностью метода Пастушенко и Шиндлера является идея последовательной оценки
узлов
1
,
jj
ψψ
−
сплайн – функции на ЭВМ в интерактивном режиме.
Многомерный случай
Рассмотренные способы кусочно-гладкой аппроксимации можно обобщить на
многомерный случай. Если, например, необходимо подобрать функцию для кусочно-гладкой
поверхности, показанной на рис. 9, то это можно сделать в несколько этапов.
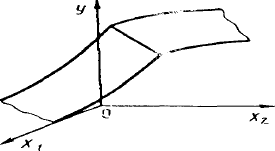
Рис. 9. Трехмерная кусочно-гладкая поверхность отклика.

12
Вначале приравняем нулю один из факторов (например, х
1
= 0). Тогда от пересечения
поверхности с плоскостью х
2
- у остается кусочно-гладкая кривая, которую можно
аппроксимировать любым из описанных выше способов. В полученной при этом функции
(
)
ψ
β
,,
2
xyy
=
(55)
β - вектор коэффициентов; ψ - вектор абсцисс точек изломов.
Далее следует найти зависимости
(
)
1
x
β
β
=
и
(
)
1
x
ψ
ψ
=
, (56)
причем функции
(
)
1
x
ψ
ψ
=
также могут описывать кривые с изломами
(
)
ψ
ψ
ψ
′
=
,
1
x
. (57)
Наконец, осталось ввести функции (56) и (57) в выражение (55) и получить искомую
аппроксимацию кусочно-гладкой поверхности (см. дальше в [Р6.5]).
Литература
1. Едвабник И. Ю., Новик Ф. С., Цейтлин Н. А. Использование двухсторонних сплайнов для
аппроксимации сложных физико-химических кривых. Зав. лаб., 1985, т.51, №3, с. 54-57.
2. Иванов О. С. - В кн.: "Теоретические и экспериментальные методы исследования диаграмм состояния
металлических систем". - М.: "Наука", 1969. - С. 120.
3. Маневич В. Е., Чернова Н. А. - В кн.: "Применение математических методов для исследования
многокомпонентных систем". - М.: "Металлургия", 1974. - С. 154.
4. Соболев Н. Н., Чемлева Т. А. – "3аводская лаборатория", 1976, № 1. - С. 70.
5. Варламов В. Л. и др. Производство кальцинированной соды и поташа при комплексной переработке
нефелинового сырья. - М.: "Химия", 1977.
6. Телитченко В. А., Цейтлин Н. А., Беляев Э. К. - Деп. рукопись, № 1571/78 деп. - Черкассы,
ОНИИТЭХИМ, 1978. - 68 с.
7. Курнаков Н. С. Введение в физико-химический анализ. - М. - Л.: Изд-во АН СССР, 1940.
8. Федоров В. В. - В кн.: "Новые идеи в планировании эксперимента". - М.: "Наука",
1969. - С. 264.
9. Chernova N. A., Melnikov Р. Р. а. о. – "Talanta", 1971, v. 8, p. 642.
10. Алберг Дж., Нильсон Э., Уолш Дж. Теория сплайнов и ее приложения. - М.: "Мир", 1977.
11. Стечкин С. Б., Субботин Ю. Н. Сплайны в вычислительной математике. - М.: "Наука", 1976.
!2. Стебаков С. А. - В кн. "Планирование эксперимента". - М.: "Наука", 1966. - С. 57.
13. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. - М.: "Наука",
1974. - 832 с.
14. Гельфанд И. М., Глаголева Е. Г., Шноль Э. Э. Функции и графики. - М.: "Наука", 1968.
15. Вол А. Е. Строение и свойства двойных металлических систем. - М.: Физматгиз, 1959. – Т 1. - 756 с.;
1962. - Т. II. - 984 с.
16. Shin С., Perretty Е. – "Trans. ASM", 1954, v. 46, p. 389.
17. Liu Т., Perretty Е. – "Trans. ASM", 1952, v. 44, p. 539.
18. Химмельблау Д. Анализ процессов статистическими методами. - М.: "Мир", 1973.
19. Новик Ф. С. – "Заводская лаборатория", 1968, № 10. - С. 1223.
20. V. P. PASTUSHENKO, H. SCHINDLER, Phil. Trans. R. Soc. Lond. B (1997) 352, 39-51, Printed in Great
Rritain; Институт Биофизики, Johannes Университет Кеплера Linz, Altenbergerstr. 69, A-4040 Linz-Auhof,
Австрия Т. (0043-732)24689267, Ф. (0043-732)246810 Vassili.Pastushenko@jk.uni-linz.ac.at
1
6.1.2. Использование двухсторонних сплайнов для аппроксимации сложных кривых
Чистая математика делает то, что можно, так, как нужно,
а прикладная - то, что нужно, так, как можно. (Из интернета)
Качество аппроксимации сложных кривых характеризуется рядом критериев:
унифицированность, но и не громоздкость вида формулы, линейность функции по
коэффициентам, степень ортогональности базисных функций (в период расчёта эмпирических
коэффициентов), адекватность случайной ошибке исходных данных, гладкость, непрерывность
или, наоборот, точное соответствие разрыву непрерывности функции, отсутствие осцилляций
при интерполяции, возможность правдоподобной экстраполяции (при последующем
использовании аппроксимирующей функции) и т. п. Задача элегантной аппроксимации кривых
имеет множество разнообразных решений. Одним из лучших является аппроксимация сплайнами
Парка. Авторы цитируемой работы [1] попытались разобраться в данной задаче сами и найти
решение для немногим более сложного случая путём некоторого усовершенствования структуры
сплайна Парка.
На практике нередко встречается задача аппроксимации сложной кривой функции одной
переменной f (х), имеющей крутые и пологие участки, разрывы непрерывности как функции, так и
ее производных. Чаще всего такая функция бывает задана своими значениями {f(x
i
)} в не
равноотстоящих точках {x
i
} (i = 1, …, N), x
1
< x
2
< … < x
N
на области (х
1
, x
N
). Использование в этих
случаях полиномиальной аппроксимации
(
)
(
)
i
i
n
i
xxfxfββ
∑
=
==
0
, (1)
не приводит к успеху, поскольку, как правило, возникают трудности с оцениванием вектора
коэффициентов
β
и качеством аппроксимации: аппроксимирующая функция осциллирует в
окрестности некоторых, особенно далеко отстоящих друг от друга точек, а также вблизи концов
интервала (х
1
, x
N
) аппроксимации [1].
Более эффективной процедурой является приближение с помощью аппроксимирующей
сплайн-функции, или просто сплайна. Будем называть сплайном [2, 3] такую функцию, которая
совпадает с некоторым многочленом степени r
i
на каждом i-том интервале (ψ
i - 1
, ψ
i
] (i = 1, …,
k), образующемся на оси абсцисс в результате разбиения области (х
1
, x
N
) определения функции
узлами
ψ
0
,
ψ
1
, …,
ψ
i – 1
,
ψ
i
, …,
ψ
k
(x
1
=
ψ
0
<
ψ
1
< … <
ψ
i – 1
<
ψ
i
< … <
ψ
k
= x
N
) на k интервалов. Из
множества известных наиболее удачной структурой обладает сплайн Парка (Park S. H. [4])
(
)
(
)
()()
0
1
000101
,,
i
i
j
j
mm
k
jjijnijii
fxxxIx
ββψβψψ
−
===
=−+−
∑∑∑
, (2)
где
{
}
()
il
l
m
,0
max
∈
= r
i
- степень полинома на интервале (
ψ
i
,
ψ
i – 1
]; k > 1; п
i
- число ограничений,
накладываемых на сплайн-функцию и её производные в узлах ψ
i
; I
01
(ψ
i
, x) - ступенчатая функция;
()()
0101
,0 npu ;,1 npu .
iiii
IxxIxx
ψψψψ
=≤=> (3)
При n
i
= 0 в точке ψ
i
сплайн-функция имеет разрыв непрерывности первого рода; j-тая
производная сплайн-функции имеет разрыв непрерывности первого рода в точке ψ
i
в том и только
в том случае, когда β
ij
≠ 0.
Недостатком структуры (2) является ограничение
{
}
()
{
}
()
i
il
l
il
li
rmmr
=
≤
=
∈−∈
−
,01,0
1
maxmax
(4)
для i = 2, …, k, ознaчaющee, что на каждом последующем интервале степень аппроксимирующего
многочлена не может быть ниже, чем на предыдущем.
В связи с этим
для случаев, когда степень многочлена на интервалах (ψ
i
, ψ
i+1
] с
увеличением i от 0 до k - 1 сначала убывает от r
0
до r
l
, а затем возрастает от r
l
до r
k–1
,
предлагается более совершенная структура сплайна. Для этого наряду со степенными
функциями
(x - ψ
i
)
j
I
01
(ψ
i
, x), (5)
усеченными слева, в структуре сплайна будем использовать степенные функции
(x - ψ
i
)
j
I
10
(ψ
i
, x), (6)
2
усеченные справа. Ступенчатая функция I
10
(ψ
i
, x) в выражении (6) определяется по аналогии с
выражением (3), как
()()
1010
,1 npu ;,0 npu .
iiii
IxxIxx
ψψψψ
=≤=>
(7)
В результате общий вид предлагаемого сплайна будет такой:
(
)
(
)
(
)
()()()
1
1
110
1
0101
,,
,
i
i
li
i
j
m
l
ijnijii
jj
mm
k
jjiiljnijii
fxxIx
xxIx
δ
ββψψ
βψβψψ
−
−
==
−
==+=
=−+
+−+−
∑∑
∑∑∑
(8)
с ограничениями
1 < l < k – 1; m
i
≥ n
i
, i = 0, …, k –1; r
i
≥ r
i + 1
при i = l, …, l - 1 и r
i
≤ r
i + 1
при i = l, …, k – 1. (9)
Сплайн-функцию (8) будем называть правосторонней, или левосторонней, или
двухсторонней, если в ней использованы соответственно только функции (5), или только (6), или
одновременно (5) и (6).
Параметрическая идентификация предлагаемых сплайнов выполняется с помощью
стандартных программ регрессионного анализа [1, 3, 5]. Для выбора числа и расположения узлов
ψ
i
используются либо физико-химические соображения, либо эмпирические правила, например,
Уолда ("выбирайте как можно меньше узлов - так, чтобы на каждом интервале было не меньше
четырех - пяти наблюдений; следите за тем, чтобы на каждом интервале было не более одной
точки перегиба; помещайте узлы Ψ
i
ближе к точкам перегиба") [3, 6]. При необходимости
значения величин ψ
i
можно оценивать наряду с остальными параметрами β
ij
методами
нелинейного регрессионного анализа [1, 5].
6.1.3. Аппроксимация сложных физико-химических кривых
Пример 1. Требуется получить аппроксимацию зависимости логарифма коэффициента
активности магния (y = lnγ
Mg
) от мольной доли висмута (х) в системе Mg-Bi по данным
экспериментального исследования [7] (точки на рис. 1). Среднеквадратичное отклонение (СО)
ошибки воспроизводимости опыта S
y
= 0,041 с числом степеней свободы f
y
= 10.
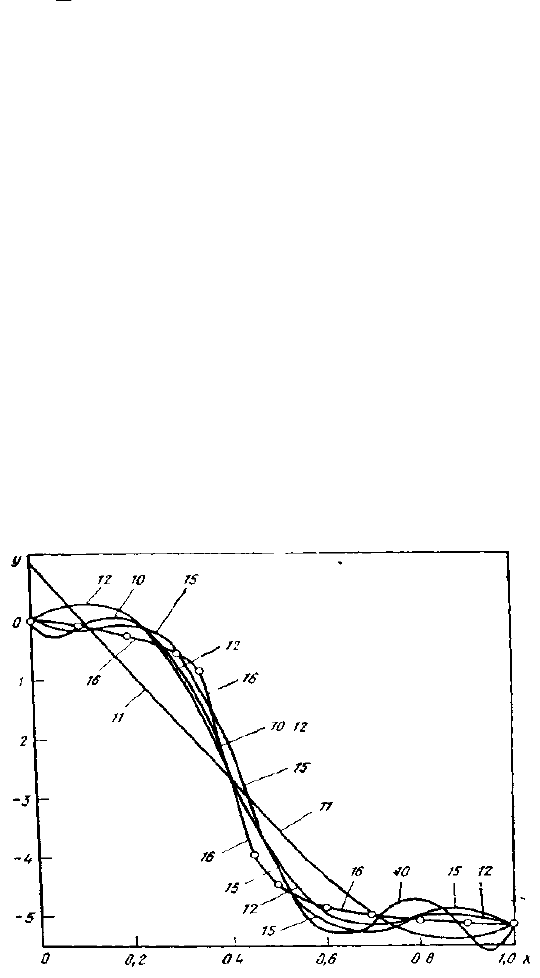
Рис. 1. Зависимость логарифма коэффициента активности магния от концентрации висмута в
системе Mg-Bi:
точки - экспериментальные данные [7], кривые - графики аппроксимирующих функций,
номера которых указаны.
Аппроксимация искомой зависимости полиномами высоких порядков не дала
положительных результатов. Так, полином десятого порядка, который после исключения
незначимых по критерию Стьюдента коэффициентов имел вид
y = 0,0122 - 14,436x + 190,208x
2
- 755,541x
3
+ 892,19х
4
- 384,21х
5
+ 66,65х
10
, (10)
дал высокое СО остаточной ошибки S
ост
= 0,49 с числом степеней свободы f
ост
= 5 и
3
характеризовался осцилляциями функции на концах отрезка (см. рис. 1).
Обратимся к аппроксимации сплайнами.
Разобьем весь отрезок (0,1) на два интервала тремя узлами ψ
0
= 0, ψ
1
= 0,4 и ψ
2
= 1.
Построенные для этого случая правосторонние кубические сплайны типа (2) - гладкий
у = 0,979 - 9,09х + 14,65(х - 0,4)
3
⋅
I
01
(0,4;х) (11)
и с разрывом непрерывности первой производной в точке ψ
1
= 0,4:
y = -0,30 + 10,3х - 40,0х
2
+[99,0(х - 0,4) - 49,9(х - 0,4)
3
]⋅I
01
(0,4; х) (12)
оказались неудовлетворительными. Сплайн (11) имел S
ост
= 0,86 с f
ост
= 9, а сплайн (12) – S
ост
= 0,45
с f
ост
= 7. Поэтому отрезок (0,1) разбили на три интервала четырьмя узлами ψ
0
= 0; ψ
1
= 0,35;
ψ
2
= 0,45; ψ
3
= 1 и рассмотрели возможность построения для такого разбиения кубического
правостороннего сплайна типа (2)
(
)
(
)
(
)
(
)
(
)
xIxxIxxy
j
jj
j
jj
,,
20122
3
11011110
3
0
ψψβψψβψβ −+−+−=
∑
∑
==
(13)
и двухстороннего сплайна типа (8)
(
)
(
)
(
)
(
)
(
)
xIxxxIxy
j
jj
j
jj
,,
20122
3
111011011
3
1
ψψβψββψψβ −+−++−=
∑
∑
==
. (14)
Сравним сплайны (13) и (14). В сплайне (13) на интервале [ψ
0
, ψ
1
) аппроксимирующей
функцией является полином третьего порядка
(
)
j
jj
x
0
3
0
ψβ−
∑
=
; на интервале (ψ
1
, ψ
2
] к нему
добавляется линейная функция β
11
(х - ψ
1
), но в целом на этом интервале он продолжает оставаться
кубическим (r
1
= 3) полиномом; наконец, на интервале (
ψ
2
,
ψ
3
] к предыдущим двум слагаемым
добавляется функция
(
)
j
jj
x
22
3
1
ψβ−
∑
=
, (r
2
= 3). Сплайн (14) на интервале [ψ
0
, ψ
1
) совпадает с
кубическим (r
1
= 3) полиномом
(
)
(
)
11011
3
1
ψββψβ−++−
∑
=
xx
j
jj
; на интервале (ψ
1
, ψ
2
]
аппроксимирующая функция является линейной β
0
+ β
1
(x - ψ
1
), r
2
= 1; на интервале (ψ
2
, ψ
3
] -
вновь кубическим полиномом
(
)
(
)
j
jj
xx
22
3
1110
ψβψββ−+−+
∑
=
, r
3
= 3. Таким образом, разница
между сплайнами (13) и (14) заключается в том, что на интервале (ψ
1
, ψ
2
] двухсторонний сплайн
(14) позволяет получить линейную аппроксимацию (см. рис. 1), а «обычный» правосторонний
сплайн (13) сделать этого не позволяет.
Двухсторонний сплайн в форме (14) с разрывом непрерывности второй производной в узлах
ψ
1
и ψ
2
после исключения незначимых коэффициентов оказался следующим
y = [-111(х - 0,35)
2
- 176(х - 0,35)
3
] I
10
(0,35; х) - 1,325 - 21,12(х - 0,35) +
+ [74,3(х – 0,45)
2
- 76,4(х - 0,45)
3
]I
01
(0,45; х), (15)
а с разрывом непрерывности первой производной в тех же узлах -
y = [27,39(х - 0,35) - 7,19(х - 0,35)
2
]I
10
(0,35; х) - 0,813 - 32,2(х - 0,35) +
+ [23,48(х – 0,45) + 23,8(х – 0,45)
2
- 21,2 (х – 0,45)
3
]I
01
(0,45; х). (16)
Остаточное СО ошибки аппроксимации сплайном (15) S
ост
= 0,39 с f
ост
= 6; сплайном (16) -
S
ост
= 0,069 с f
ост
= 5 (см. рис. 1). Гипотеза об адекватности сплайна (16) не была отвергнута,
поскольку расчетное значение критерия Фишера
F
ˆ
= 0,069
2
/0,0414
2
= 2,8 оказалось меньше
критического F (0,05; 5; 10) = 3,33 при обычном уровне ответственности за выводы - 5 %-ном
уровне значимости [Т2Р1]. Таким образом, аппроксимацию зависимости у = lnγ
Mg
от
концентрации Bi сплайном (16) следует признать вполне удовлетворительной.
Отметим, что по физико-химическому смыслу рассматриваемой зависимости, при х = 0
должно выполняться условие у = 0. Сплайн (16) обеспечивает выполнение этого условия, так как
легко показать, что его невязка в точке х = 0, составляющая 0,0034 и по критерию Стьюдента
отличается от нуля незначимо.
Пример 2. Требовалось построить аппроксимацию кривой ликвидус диаграммы состояния
In-Sb с устойчивым химическим соединением InSb и двумя эвтектиками в частных системах In-
InSb и InSb-Sb по данным работы [8]. Кривая ликвидус (см. рис. 2) состоит из двух гладких
участков с изломом в точке кристаллизации двойной эвтектики (InSb + Sb). СО ошибки
воспроизводимости опыта S
y
= 0,88
о
C с числом степеней свободы f
y
= 10.
Визуальный анализ кривой ликвидус (см. рис. 2) свидетельствует о том, что полином слева
