Бусыгин Ю.Н. Финансирование и кредитование инвестиций
Подождите немного. Документ загружается.


151
10.3. Доход, курсовая стоимость и доходность бескупонной
облигации
Облигация такого вида обеспечивает доход за счет разницы между
номинальной стоимостью облигации и ее рыночной ценой (дисконтный
доход). Формализуем данное высказывание. Так, если облигация имеет
номинальную стоимость N, а покупная цена (рыночная) составляет Р, то-
гда доход от облигации составит:
D = N – P. (10.3.1)
Используя формулу (10.2.1.), выражение (10.3.1.) примет вид:
D = 1
100
k
P
N
⋅ −
. (10.3.2)
Доход здесь рассматривается в денежном выражении, который и
образует дисконтный доход такой облигации.
Перейдем непосредственно к рассмотрению курсовой стоимости та-
кой облигации.
Прежде всего отметим, что определение курсовой стоимости любой
ценной бумаги основано на принципе дисконтирования. Инвестор приоб-
ретает ценную бумагу, чтобы получать доходы, которые она приносит.
Поэтому для ответа на вопрос, сколько сегодня должна стоить та или иная
ценная бумага, необходимо определить дисконтированную стоимость всех
доходов, которые она приносит.
Общий принцип расчета курсовой стоимости состоит из трех дейст-
вий: 1) определяем поток доходов, которые ожидаются по данной бумаге;
2) находим дисконтированную (современную) стоимость величины каждо-
го платежа по ценной бумаге; 3) суммируем дисконтированные стоимости.
Данная сумма и представляет собой курсовую стоимость ценной бумаги.
Так как мы имеем бескупонную облигацию, т.е. текущих выплат
нет, то современная стоимость потока доходов нулевая.
Достаточно найти современную стоимость номинала, которая и бу-
дет определять курсовую стоимость облигации на момент оценки.
Пусть облигация куплена за n лет до погашения. Дисконтируем но-
минальную стоимость облигации N по годовой сложной процентной став-
ке j, которая принимает значения доходности альтернативного вложения
денежных средств с таким же сроком и риском, размер доходности кото-
рой определяется на рынке ценных бумаг.

152
Курсовая стоимость такой облигации составит
P =
(1 )
n
N
j
+
. (10.3.3)
Это есть максимальная цена, по которой целесообразно покупать
данную облигацию. Тогда, в соответствии с (10.2.1), курс облигации на
момент ее оценки составит:
P
k
=
100
(1 )
n
j
+
. (10.3.4)
Становится понятным, что для такой облигации курс всегда меньше
100. Как правило, облигации такого вида имеют короткий срок погашения
(до года). Так, государственные краткосрочные облигации (ГКО) имеют
срок погашения от 3 до 12 месяцев. В этом случае курсовая стоимость
ГКО будет определяться по формуле:
P =
1 /365
N
i t+ ⋅
, (10.3.5)
где Р – курсовая стоимость ГКО; N – номинал ГКО; i – доходность
ГКО; t – количество дней от момента покупки до погашения ГКО.
Доход и курсовая стоимость бескупонной облигации рассматри-
ваются в денежном выражении. Их значения не дают должного ответа на
вопрос, на сколько эффективно инвестор вкладывает свои денежные сред-
ства.
Реальным же показателем прибыли от проведения операций на
фондовом рынке является доходность. Это наиболее существенный пара-
метр облигации. Сравнивая доходность от различных операций на финан-
совом рынке, можно определить, в какой финансовый инструмент выгод-
нее вложить деньги.
Определим доходность от покупки такой облигации, используя эф-
фективную ставку простых процентов i
эп
. Если инвестор вложил денеж-
ные средства в размере Р на покупку облигаций в некоторый банк под
простую эффективную процентную ставку i
эп
на срок погашения (t/к), то
наращенная сумма S примет значение:
S = 1
ýï
t
P i
K
⋅ + ⋅
, (10.3.6)

153
где t – интервал времени, за который гасится облигация; к – размер
финансового года. Как правило, за финансовый год принимается 360
дней, за исключением ГКО и других государственных займов, где к= 365.
Используя формулу (10.2.1.), имеем:
S = 1
100
k
ýï
P N
t
i
k
⋅
⋅ + ⋅
. (10.3.7)
Тогда доход от покупки такой облигации составит:
D = S – P = 1
100 100 100
k k k
ýï ýï
P N P N P N t
t
i i
k k
⋅ ⋅
⋅ + ⋅ − = ⋅
. (10.3.8)
Сопоставив выражения (10.3.2) и (10.3.8), имеем:
1
100 100
k k
ýï
P N t P
i N
k
⋅
⋅ = ⋅ −
.
Отсюда, сделав ряд преобразований, получим:
i
эп
=
(100 )
k
k
P k
P t
− ⋅
⋅
. (10.3.9)
Если для измерения доходности использовать эффективную ставку
сложных процентов j
эс
, то величина наращенной суммы S примет вид
S = P(1+j
эс
)
t/k
. (10.3.10)
Тогда доход от покупки такой облигации составит:
D = S – P =
/ /
(1 ) (1 ) 1
100
t k t k
k
ýc ýñ
P N
P j P j
⋅
⋅ + − = + −
. (10.3.11)
Сопоставив выражения (10.3.2) и (10.3.11), имеем:
/
(1 ) 1 1
100 100
t k
k k
ýñ
P N P
j N
⋅
+ − = ⋅ −
.

154
Отсюда, сделав некоторые преобразования, получим:
j
эс
=
/
100
1
t k
k
P
−
. (10.3.12)
П р и м е р 10.1. Инвестор решил приобрести 10 государственных
краткосрочных облигаций (ГКО) номиналом по 100 тыс. руб. со сроком
погашения 60 дней и доходностью 15% годовых.
Какова максимальная рыночная цена, по которой инвестор сможет
приобрести эти облигации?
Решение.
Здесь N = 100000, t = 60, к = 365, i= 0,15%.
По формуле (10.3.5) определим курсовую стоимость одной облига-
ции
P =
100000
97593,6
1 0,15 60/365
=
+ ⋅
руб.
Тогда суммарная цена 10 облигаций составит 975936 руб.
П р и м е р 10.2. Беcкупонная облигация номиналом 120 тыс. руб.
размещается сроком на 3 года. Процентная ставка по альтернативному
вложению с таким же сроком и риском, как данная облигация, равна 20%.
По какой максимальной курсовой стоимости ее можно купить? Каков курс
данной облигации?
Решение.
Здесь N = 120, n = 3, j = 0,2. Используя формулу (10.3.3), определим
курсовую стоимость облигации
P =
3
120
69,444
(1 0,2)
=
+
тыс. руб.
По формуле (10.3.4) находим курс данной облигации
Р
к
=
3
100
57,87%
(1 0,2)
=
+
П р и м е р 10.3. Десять бескупонных облигаций по 50 тыс. руб.
продаются по курсу 95%, срок обращения которых 90 дней. Какова общая
сумма дохода от приобретения этих облигаций? Какова доходность об-
лигации такого вида?

155
Решение.
Здесь N = 50, Р
к
= 95, t = 90, к = 360.
По формуле (10.3.2) находим доход от приобретения одной облига-
ции:
D =
95
50 1 2,5
100
⋅ − =
тыс. руб.
Доход от покупки 10 таких облигаций составит:
D = 2,5⋅10 = 25 тыс. руб.
Так как срок погашения облигации меньше года, то для определе-
ния доходности от покупки облигации используем формулу (10.3.9):
i
эп
=
(100 95) 360
21,05%
95 90
− ⋅
=
⋅
П р и м е р 10.4. Инвестор приобрел на аукционе 20 облигаций по
номинальной стоимости 100 тыс. руб., каждая по курсу 90%, со сроком
погашения 2 года. Определить общую сумму дохода от такой сделки и
доходность такой облигации, используя эффективную ставку простых и
сложных процентов. Результаты расчетов сопоставить.
Решение.
Здесь N = 100, Р
k
= 90, п = 2, t = 720, к = 360.
По формуле (10.3.2) находим доход от приобретения одной облига-
ции:
90
100 1 100 0,1 10
100
D
= ⋅ − = ⋅ =
тыс. руб.
Доход от покупки 20 облигаций составит:
D = 20⋅10 = 200 тыс. руб.
Используя формулу (10.3.9), определим доходность такой облига-
ции по эффективной ставке простых процентов:
i
эп
=
(100 90) 360
0,056
90 720
− ⋅
=
⋅
, или 5,6%

156
Доходность облигации по эффективной ставке сложных процентов
определим по формуле (10.3.12).
В результате буем иметь:
j
эс
=
100
1 0,054 5,4%
90
− = =
.
Сопоставив результаты расчета доходности такой облигации по
ставкам простых и сложных процентов, видим, что доходность их не-
сколько выше, если проводить расчеты по эффективной ставке простых
процентов.
10.4. Моделирование расчетных показателей купонной облига-
ции с периодической выплатой процентов и их реинвестированием
Операции с этим видом облигаций осуществляются в основном с
частными лицами. Доход в этом случае будет состоять из купонного дохо-
да D
k
и разницы между номиналом N и ценой покупки Р:
D = D
к
+ (N – P). (10.4.1)
Используя выражение (10.2.1), имеем:
D =
1 ,
100
k
k
P
D N
+ ⋅ −
(10.4.2)
где Р
к
– курс купонной облигации.
Будем считать, что проценты, получаемые в течение срока облига-
ции, реинвестируются. В этом случае значение D
к
будет определяться как
наращенная сумма постоянной ренты постнумерандо, размер платежа ко-
торой равен:
R
q
=
,
q
iN
k
⋅
(10.4.3)
где q – количество выплат купонных процентов по облигации в те-
чение года; i
к
– купонный процент.
Если купонные выплаты по облигации в течение п лет осуществля-
ются q раз в год и получаемые купонные проценты вновь инвестируются

157
по ставке i
р
с начислением на них процентов m раз в год (m/q), то значение
D
к
в соответствии с и (10.4.3) будет равно:
D
k
=
( )
/
1 1 /
.
(1 / ) 1
mn
p
k
m q
p
i m
N i
q i m
−
− +
⋅
⋅
+ −
(10.4.4)
Следовательно, общий доход инвестора составит
D = D
k
+ (N – P) =
( )
/
1 1 /
1 .
100
(1 / ) 1
mn
p
p
k
m q
p
i m
N i
P
N
q i m
−
− +
⋅
⋅ + ⋅ −
+ −
(10.4.5)
Для определения курсовой стоимости данной облигации используем
общий принцип ее расчета, описанный выше: определим дисконтирован-
ную стоимость номинала, дисконтированную стоимость величины буду-
щих купонных доходов и полученные значения просуммируем.
Данная сумма и будет представлять курсовую стоимость купонной
облигации.
Пусть i
к
, i
р
– ставка купона и ставка реинвестирования (дисконтиро-
вания) процентных денег, которая соответствует уровню риска, устано-
вившемуся на рынке ценных бумаг. Если облигация номиналом N куплена
за п лет до ее погашения, купонные выплаты осуществляются q раз в год и
полученные купонные проценты вновь инвестируются m раз в год по но-
минальной процентной ставке i
р
, то размер платежа (будущие купонные
доходы), определяемые формулой (10.4.3), есть годовая финансовая рента.
Тогда дисконтированная стоимость номинала будет определяться
формулой:
P
n
=
.
)1(
n
p
i
N
+
(10.4.6)
Дисконтированная стоимость финансовой ренты в соответствии с
формулами (10.4.3) и (10.4.4) составит
P
q
=
(
)
.
1)/1(
/11
/
−+
+−
⋅
⋅
−
qm
p
mn
p
k
mi
mi
q
iN
(10.4.7)
Следовательно, курсовая стоимость такой облигации будет опреде-
ляться выражением:

158
P = P
q
+ P
n
=
( )
/
1 1 /
,
(1 / ) 1 (1 )
mn
p
k
m q n
p p
i m
N i
N
q i m i
−
− +
⋅
⋅ +
+ − +
10.4.8)
а курс облигации такого вида будет равен:
P
k
=
⋅
⋅
q
i
k
100
[
( )
/
1 1 /
1
].
(1 / ) 1 (1 )
mn
p
m q n
p p
i m
i m i
−
− +
+
+ − +
(10.4.9)
Положив в формуле (10.4.9) m = n = q = 1, имеем:
P
k
=
1
1 (1 )
.
(1 )
p
k
p p
i
N
N i
i i
−
− +
⋅ ⋅ +
+
(10.4.10)
Поскольку дисконтированная стоимость ренты больше нуля, из
приведенной формулы (10.4.10) можно сразу же сделать следующие выводы:
1. Если купонная ставка i
к
равна текущей процентной ставке i
р
, то
курсовая стоимость равна номинальной стоимости облигации.
2. Если купонная ставка i
к
меньше текущей процентной ставки
i
р
(i
к
< i
р
), то курсовая стоимость меньше номинальной. В этом случае го-
ворят, что облигация куплена с дисконтом. Поскольку при низкой купон-
ной ставке для инвесторов предпочтительнее вложение средств в более
доходные финансовые инструменты, то продажа облигации по цене ниже
номинала дает возможность получения дополнительного дохода.
3. Если купонная ставка выше i
к
номинальной процентной ставки
i
р
(i
к
> i
р
), то курсовая стоимость выше номинальной (курс выше 100). В
этом случае облигация продается с премией. Поскольку купонная ставка
выше текущей процентной ставки, то для уравнивания доходности с ры-
ночной курсовая стоимость должна быть выше номинальной на величину
премии, которая уменьшает доходность операции до i
р
.
Оценка облигации производится не только в момент эмиссии, но и в
любой момент времени вплоть до момента погашения. В любой момент
времени облигация может быть продана или приобретена на рынке ценных
бумаг по рыночной цене. Наиболее просто оценивается облигация перед
погашением, в купонном периоде, когда предстоит только выплата за по-
следний купон и сам номинал, т.е. выплата в размере N(1+ i
k
). Если интер-
вал времени от момента оценки до момента погашения равен t, то, дискон-
тируя величину выплаты на этот интервал времени по ставке i
p
, получим
текущую стоимость облигации:
159
P (t) =
.
)1(
)1(
t
p
k
i
iN
+
+⋅
(10.4.11)
Отсюда
=
100
)(tP
k
.
)1(
)1(
t
p
k
i
i
+
+
(10.4.12)
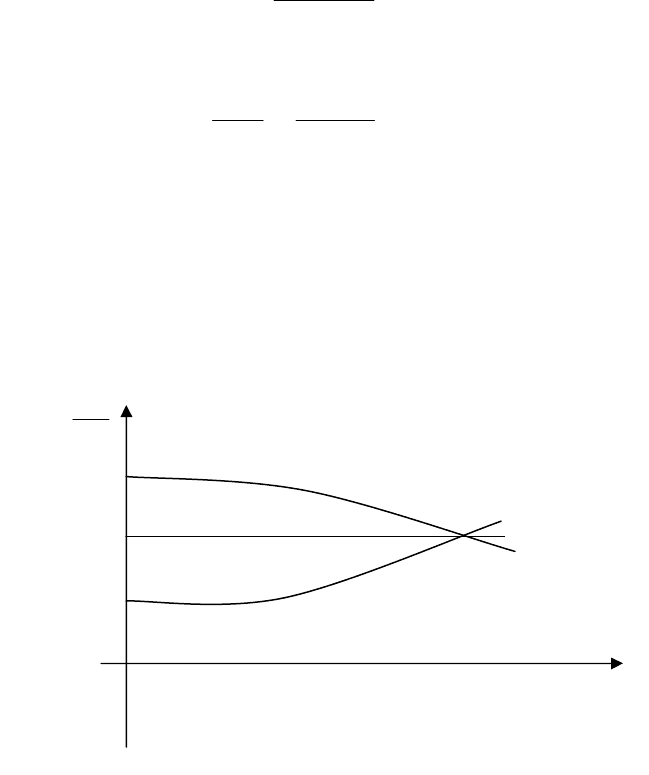
Из формулы (10.4.12) видно, курс облигации изменяется во време-
ни по мере приближения к дате погашения даже при постоянной текущей
процентной ставке i
р
. Если облигация была куплена с дисконтом (i
к
< i
р
),
то курс облигации возрастает по мере приближения к дате погашения
(происходит накопление дисконта). Если облигация была куплена с пре-
мией (i
к
> i
р
), то по мере приближения к сроку погашения происходит
уменьшение ее курса (происходит возмещение премии). Указанная зави-
симость может быть представлена графически (рис. 10.5).
Рис. 10.5. Зависимость курсовой стоимости от времени
(рыночная ставка i
р
= 0,10)
Теперь определим доходность облигации рассматриваемого типа,
используя эффективную ставку сложных процентов j
эс
.
Пусть инвестор купил купонную облигацию номиналом N с перио-
дической выплатой процентов q раз в год по курсовой стоимости Р со сро-
100
k
P
i
p
= 0,15
i
p
= 0,10
1
i
p
= 0,05
0 1 2 3 4 5 6 время
160
ком погашения через n лет. При этом полученные купонные проценты
вновь инвестируются m раз в год.
Для определения эффективной ставки сложных процентов j
эс
будем
рассуждать как в п. 10.3. В этом случае расчетная формула дохода, полу-
чаемого от покупки такой облигации, имеет вид:
D = S – P = P (1 + j
эс
)
n
– P . (10.4.13)
Отсюда
j
эс
=
1
n
P D
P
+
−
. (10.4.14)
Используя формулы (10.4.1) и (10.4.2) имеем
j
эс
=
100 ( )
1,
k
n
N D
P
⋅ +
−
(10.4.15)
где купонный доход D
к
может быть рассчитан по формуле (10.4.4).
Отметим, что между курсовой стоимостью Р и ее доходностью j
эс
до
погашения облигации существуют следующие зависимости:
1. Цена облигации и доходность до погашения находятся в обратной
связи. При повышении доходности цена облигации падает, при понижении
– возрастает.
2. Если доходность до погашения выше купонного процента, обли-
гация продается со скидкой.
3. Если доходность до погашения ниже купонного процента, обли-
гация продается с премией.
4. Если доходность до погашения равна купонному проценту, цена
облигации равна номиналу.
5. При понижении доходности до погашения на 1%, цена облигации
возрастает в большей степени в сравнении с ее падением при увеличении
доходности до погашения на 1%.
П р и м е р 10.5. В 2002 г. Минфин Республики Беларусь разместил
облигации государственного сберегательного займа (ОСЗ), номинальной
стоимостью 100 тыс. руб. сроком на один год с купоном 80% годовых.
Выплата процентов осуществлялась 4 раза в год.
Инвестор приобрел 10 таких облигаций по курсу 90%. Процентные
деньги вновь инвестировались по номинальной процентной ставке 80% с
начислением процентов 4 раза в год. Определить доход инвестора от по-
купки таких облигаций и эффективную процентную ставку.
