Буслаев А.П., Лебедев А.А., Яшина М.В. Моделирование потоков на графах. Теоретические и вычислительные аспекты. Часть 1. NODE-модель трафика
Подождите немного. Документ загружается.


42
среднюю мощность.
Неотрицательная величина
Q
∗
=
1
T
T
∫
0
x (t) dt (12)
является средней длиной очереди за рассматриваемый сег-
мент времени.
Если C - масса потока на контуре, то решение T
∗
уравнения
T
∗
∫
0
f (ρ (t)) dt = C (13)
определяет среднее время оборота потока.
Пусть T
∗
min
= min T
∗
, тогда величина
T
∗
− T
∗
min
T
∗
min
называется относительной задержкой.
3.1.3. Оптимизация работы потока на элементарном контуре
Пусть θ(t) — любая бинарная {0, 1} функция, которая обес-
печивает посредством конечного числа переключений перио-
дическое изменение параметров системы, T — период.
Тогда на фазовой кривой каждая точка траектории прохо-
дит четное количество раз в противоположных направлениях
с соответствующей направлению скоростью. При этом отно-
шение скоростей в силу параллельности касательных векто-
ров пропорционально отношению, например первых коорди-
нат |
˙
x|, т.е.
{
(|s − f(ρ)|, f(ρ)), if x > 0,
(0, f(ρ)), if x = 0.
Следовательно, при x > 0 вклад работы траектории в окрест-
ности фиксированной точки x, ρ на взаимно противополож-
ных направлениях равен
M
+
=
(1 − x)f(ρ) + sx)f(ρ) + (s − f(ρ))(1 − x)f(ρ)
√
(s − f(ρ))
2
+ (f(ρ))
2
=

43
=
sf(ρ)
√
(s − f(ρ))
2
+ (f(ρ))
2
. (15)
Значит, на фазовой траектории наиболее значимыми точками
будут те, для которых достигается максимум M
+
.
Аналогично в случае x = 0 получаем
M
0
= (1 − x)f(ρ) + sx = f(ρ). (16)
Максимальное значение функции M
0
(16) часто называют
пропускной способностью транспортной сети. В случае (15)
M
+
не зависит явно от длины очереди x
M
+
=
S
√
(
S
f(ρ)
− 1)
2
+ 1
. (17)
Экстремум функции (17) достигается в точках,
где
(
(
S
f(ρ)
− 1
)
2
)
′
⇔ f
′
(ρ) = 0 или S = f(ρ).
Но поскольку S > max
0≤ρ≤1
f(ρ), то точки экстремума для (16)
и (17) совпадают ρ
∗
= 0 , 5 при условии, что удовлетворяются
ограничения.
Следовательно, в случае x > 0 получаем
0, 5(1 − x) + 1 · x = C, (18)
откуда x = 2C − 1. Значит, при C ≥ 1/2 имеем следующую
оптимальную точку на фазовой плоскости
x
∗
= 2 C − 1, ρ
∗
= 0, 5. (19)
При C <
1
2
в силу
(
S
f(ρ)
− 1)
2
= 1
2
≤ (
S
f(ρ)
− 1 + 1)
2
получаем, что
M
+
≥ S/(S/f(ρ)) = f(ρ) = M
0
. (20)
Таким образом, при C <
1
2
оптимальная точка на фазовой
плоскости
x
∗
= 0+, ρ
∗
= C. (21)

44
Периодические колебания в окрестности точки (19) фазо-
вой плоскости оптимизируют работу потока при C >
1
2
и в
правой окрестности точки (21) — в случае C <
1
2
.
3.1.4. Оптимизация работы потока на транспортном цветке
Рассмотрим множество режимов функционирования узла
следующего вида: пусть
0 < T
1
< T
1
+ T
2
< T
1
+ T
2
+ T
3
<
˙
S < T
1
+ T
2
+ ... + T
n
= T.
Для лепестка с номером i определим (0 ≤ t ≤ T )
θ
i
(t) =
{
1, T
1
+ ˙s + T
i−1
< t < T
1
+ · · · + T
i−1
+ T
i
,
0, else.
По прошествии времени T функции периодически повторя-
ются.
Для упрощения предположим, что
ST
i
≥ C
i
, i = 1, . . . , n, (22)
т. е. в каждом цикле очередь "рассасывается". Значит, начи-
ная со второго цикла, поведение потоков на каждом лепестке
имеет тот же период T независимо от начальных условий.
С точностью до замены переменных можно считать, что для
∀1 ≤ i ≤ n :
1) в начальный момент масса распределена равномерно по
лепестку ρ
i
= C
i
и интенсивность движения f(ρ
i
);
2) в течение времени 0 < t < T − T
i
узел перекрыт и на-
капливается очередь со скоростью f(ρ
i
(t));
3) затем в течение некоторого промежутка (T −T
i
, T −T
i
α
i
)
0 < α
i
≤ 1 , происходит "рассасывание"очереди;
4) наконец, при t ∈ [T − T
i
α
i
, T ] масса равномерно распре-
делена по кольцу.
Число α
i
однозначно определяется параметрами C
i
и T
i
,
1 ≤ i ≤ n.
Обозначим через A(C
i
, T
i
, T ) работу потока на лепестке с
номером i. Тогда цель оптимизации состоит в поиске распре-
45
деления вектора T
i
, 1 ≤ i ≤ n такого, что
Σ
n
i=1
A(C
i
, T
i
, T ) → max = A(C
1
, ..., C
n
, T ) (23)
при условии
Σ
n
i=1
T
i
= T, (24)
T
i
≥ C
i
/S, i = 1, ...n. (25)
Ясно, что для корректности постановки задачи (22) - (25)
необходимо, чтобы
T ≥ C/S,
где C− полная масса потока на цветке.
3.1.5. Оптимизация массы потока на лепестках
Задача
A(C
1
, ..., C
n
, T ) → max (26)
при условии
Σ
n
i=1
C
i
= C (27)
позволяет ответить на вопрос о максимально возможной ра-
боте потока фиксированной массы C на цветке. Например,
достаточное условие того, что решение (25) достигается на
векторе с равными координатами состоит в том, чтобы функ-
ция A была вполне положительной или если бы все Θ
i
≡ 1 .
3.1.6. Динамическая система Инь-Янь с управлением
Поток Инь-Янь
Рассматривается граф с двумя узлами и соединяющими их
ребрами с односторонним движением. Пусть длины ребер рав-
ны 1.
Состояние системы на каждом ребре представляется сле-
дующим вектором:
((x
i
, ρ
max
), (y
i
, ρ
i
)) , i = 1, 2, (28)
где x
i
– часть ребра, входящего в i-вершину, на котором плот-
ность потока максимальна (накопитель), (y
i
, ρ
i
) – остальная
часть ребра и соответствующая плотность потока.
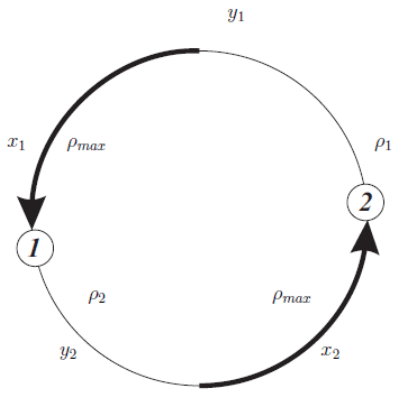
46
Рис. 41. Инь-Янь
Будем считать, что ρ
max
= 1. Пусть C - масса потока на
графе, константа для замкнутой системы.
Предположим, что
f(u) = u(1 − u) (29)
- интенсивность потока плотности u, 0 ≤ u ≤ 1. Пусть S -
интенсивность убывания потока максимальной плотности пе-
ред соответствующим узлом (перекрестком), R - максималь-
но возможная интенсивность на перекрестке (пропускная спо-
собность).
0 < S < R. (30)
Пусть далее θ
i
(t) - кусочно-постоянные функции, прини-
мающие значения 0 и 1, которые моделируют светофорную
сигнализацию на соответствующем перекрестке, где "0" – за-
прет движения, а "1" – разрешение.
Таким образом, для параметров (28) системы справедливы
следующие соотношения (i = 1, 2):
x
i
≥ 0, y
i
≥ 0 , (31)
x
i
+ y
i
= 1, (32)
0 ≤ ρ
i
≤ 1 = ρ
max
, (33)
x
1
· 1 + y
1
· ρ
1
+ x
2
· 1 + y
2
· ρ
2
= C. (34)
47
С учетом соотношений (31) – (34) состояние динамической
системы можно описать параметрами x
1
, ρ
1
, x
2
, ρ
2
, для ко-
торых справедливы следующие дифференциальные соотно-
шения:
x
1
(t) =
=
{
−θ
1
(t) S + f (ρ
1
) ; x
1
> 0,
(1
− θ
1
(
t
))
f
(
ρ
1
) +
θ
1
(
t
) (
f
(
ρ
1
)
− R
)
+
; x
1
= 0.
(35)
(ρ
2
(1 − x
2
))
·
=
=
θ
1
(t) S − f (ρ
2
) ; x
1
> 0, x
2
> 0,
θ
1
(t) S − θ
2
(t) min (f (ρ
2
) , R) ; x
1
> 0 , x
2
= 0 ,
θ
1
(t) min (f (ρ
1
) , R) − f (ρ
2
) ; x
1
= 0 , x
2
> 0 ,
θ
1
(t) min (f (ρ
1
) , R) − θ
2
(t) min (f (ρ
2
) , R) ; x
1
= 0 , x
2
= 0 ,
(36)
˙x
2
(t) =
=
{
−θ
2
(t) S + f (ρ
2
) ; x
2
> 0,
(1 − θ
2
(t)) f (ρ
2
) + θ
2
(t) (f (ρ
2
) − R)
+
; x
2
= 0.
(37)
(ρ
1
(1 − x
1
))
·
=
=
θ
2
(t) S − f (ρ
1
) ; x
1
> 0, x
2
> 0,
θ
2
(t) S − θ
1
(t) min (f (ρ
1
) , R) ; x
1
= 0 , x
2
> 0 ,
θ
2
(t) min (f (ρ
2
) , R) − f (ρ
1
) ; x
1
> 0 , x
2
= 0 ,
θ
2
(t) min (f (ρ
2
) , R) − θ
1
(t) min (f (ρ
1
) , R) ; x
1
= x
2
= 0 .
(38)
В уравнениях (35)-(38) использовано обозначение
(A − B)
+
= {A − B, A > B; 0, A ≤ B} .
Уравнения (35), (37) описывают динамику накопителей пе-
ред перекрестками в зависимости от функции управления θ
i
(t) ,
i = 1, 2. Уравнения(36),(38) отображают изменение массы на
основных частях звеньев в зависимости от состояния нако-
пителей ("пуст"( ⇐⇒ x
i
= 0), "непуст"( ⇐⇒ x
i
> 0)) и
функций управления перекрестками.

48
Рис. 42. Кратный узел
Цель работы состоит в исследовании свойств решений си-
стемы (35)-(38) в зависимости от параметров. В частности,
каково асимптотическое поведение решений для различных
сценариев управления θ
1
(t) , i = 1, 2?
Весьма интересным является также возможность адаптив-
ного управления потоком, т.е. оптимизации управления по
мере получения информации о состоянии системы. Важный
частный случай: узлы 1 и 2 (рис. 41) моделируют пересекаю-
щиеся направления движения на одном перекрестке (рис. 42).
При этом естественно предположить, что
θ
1
(t) + θ
2
(t) ≡ 1, (39)
т.е. в текущий момент времени одно направление открыто,
другое закрыто.
Как управлять таким перекрестком?
Простейший случай
Пусть в (35)-(38)
θ
1
(
t
)
≡ θ
2
(
t
)
≡ 1, (40)
max f (s) ≤ min (S, R) = S. (41)
Система (35)-(38) принимает вид
˙x
1
(t) =
{
−s + f (ρ
1
) ; x
1
> 0
0; x
1
= 0
(42)

49
(ρ
2
(1 − x
2
))
·
=
{
s − f (ρ
2
) ; x
1
> 0, x
2
≥ 0
f (ρ
1
) − f (ρ
2
) ; x
1
= 0 , x
2
≥ 0
(43)
˙x
2
(t) =
{
−s + f (ρ
2
) ; x
2
> 0
0; x
2
= 0
(44)
(
ρ
1
(1
− x
1
))
·
=
{
s − f (ρ
1
) ; x
1
≥ 0 , x
2
> 0
f (ρ
2
) − f (ρ
1
) ; x
1
≥ 0, x
2
= 0 .
(45)
Предположим, что в начальный момент заданы значения
(x
1,0
, ρ
1,0
) , (x
2,0
, ρ
2,0
) .
Тогда из (42) следует, что либо x
1
≡ 0, либо x
1
(t) убывает
монотонно к нулю с отделенной от нуля скоростью, т. е. об-
ратится в нуль за конечное время. Аналогичное верно и для
x
2
(t). Таким образом,
x
1
(t) ≡ x
2
(t) ≡ 0, (46)
начиная с некоторого момента T
0
. Поэтому из (42)-(45) сле-
дует, что при t ≥ T
0
{
˙ρ
1
= f (ρ
2
) − f (ρ
1
)
˙ρ
2
= f (ρ1) − f (ρ
2
) .
(47)
При этом тождество (34) обращается в
ρ
2
+ ρ
1
≡ C. (48)
Система (47)-(48) исследована в [1], где установлено, что
при
C < ρ
max
= 1 (49)
для любых начальных условий решения сходятся к равновес-
ной точке
ρ
1
≡ ρ
2
≡
C
2
,
а при C > ρ
max
= 1 для любых начальных условий решение
(47)-(48) за конечное время выходит на границу
(ρ
1
≡ 1 , ρ
2
= C − 1) ∨ (ρ
1
= C − 1, ρ
2
≡ 1) ,
что соответствует затору.

50
Рис. 43. Перекресток 1-2
Тождественное управление и элементарный контур
Предположим, что
θ
1
(t) ≡ θ
2
(t) ≡ θ(t) (50)
– периодические функции, причем на периоде T = T
1
+ T
2
имеется лишь одна перемена значения, т. е.
θ
i
(t) = 1, 0 < t < T
1
; 0, T
1
< t < T , i = 1, 2.
Соотношение (41) предполагаем справедливым. Рассматри-
ваемый случай может быть интерпретирован следующим об-
разом.
На рис. 43 узлы 1 и 2 относятся к одному перекрестку, ко-
торый пересекает внешний по отношению к рассматриваемой
замкнутой системе поток.
Динамическая система (см. рис. 43) состоит из двух несвя-
занных контуров. Если положить θ
3
(t) = 1 − θ(t), то получим
элементарную систему с накопителем (рис. 44).
Для простоты будем считать, что x
3
+y
3
= 1; ρ
max
, S и f(ρ)
определены ранее. Имеем следующие соотношения:
˙x
3
=
{
−θ
3
(t)S + f(ρ
3
); x
3
> 0,
(1 − θ
3
(t)) f (ρ
3
) ; x
3
= 0 .
(51)
(ρ
3
y
3
)
·
=
{
θ
3
(t) S − f (ρ
3
) ; x
3
> 0,
− (1 − θ
3
(t)) f (ρ
3
) ; x
3
= 0.
(52)

51
Рис. 44. Элементарный контур
В зависимости от значения θ
3
получаем два вида автоном-
ных систем: если θ
3
= 1 , то
˙x
3
(t) =
{
−s + f (ρ
3
) ; x
3
> 0
0; x
3
= 0 ,
(53)
если θ
3
= 0 , то
(ρ
3
y
3
)
·
=
{
s − f (ρ
3
) ; x
3
> 0
0; x
3
= 0 .
(54)
Поскольку (ρ
3
y
3
)
·
= ˙ρ
3
y
3
+ ρ
3
˙y
3
= ρ
3
(1 − x
3
) − ρ
3
˙x
3
,
то при x
3
> 0
˙ρ
3
(1 − x
3
) = ˙ρ
3
x
3
+ (s − f (ρ
3
)) = (s − f (ρ
3
)) (1 − ρ
3
) ,
т.е.
{
˙ρ
3
=
(1−ρ
3
)
(1−x
3
)
(s − f (ρ
3
))
˙x
3
= − (s − f (ρ
3
))
, if x
i
> 0 . (55)
Из (55) следует, что
dρ
3
dx
3
= −
(1 − ρ
3
)
(1 − x
3
)
,
откуда
(1 − ρ
3
) (1 − x
3
) = C. (56)
На квадрате области допустимых значений 0 ≤ x
3
, ρ
3
≤ 1
семейство (56) имеет вид, показанный на рис. 45.
В силу условия (41) x
3
монотонно убывает при открытом
узле (θ
3
≡ 1) .
