Буслаев А.П., Лебедев А.А., Яшина М.В. Моделирование потоков на графах. Теоретические и вычислительные аспекты. Часть 1. NODE-модель трафика
Подождите немного. Документ загружается.


32
Рис. 30. Вкладка "План управления"(в первоначальном состоянии – план еще не
задан)
Рис. 31. Диалоговое окно добавления записи в план управления
межутков этот момент относится, и открывается соответству-
ющий вход. Приходящий с него поток распределяется в со-
ответствии с параметрами таблицы распределения для этого
входа. Остальные входы закрыты (равносильно обнуленной
строке в таблице распределения).
2.6. Задания для самостоятельной работы
Для закрепления изложенного материала предлагается ряд
заданий.
1) В чем основное отличие приложения FlowNetworkB.exe от

33
Рис. 32. Вкладка "План управления"после добавления первой записи
части FlowNetworkA.exe?
2) Опишите процесс построения графа и его редактирова-
ния. Отличается ли он от аналогичных действий при ис-
пользовании приложения FlowNetworkA.exe?
3) Что будет, если ребра графа в результате коррекции пе-
ресекутся?
4) Создайте граф, имеющий следующий вид: четыре узла
в вершинах прямоугольника из ребер и еще один узел в
центре; центральный узел соединен с каждым из первых
четырех узлов; все ребра двунаправленные. Таким обра-
зом, в графе будет пять узлов и восемь двунаправленных
ребер.
5) Как открыть диалоговое окно изменения параметров рас-
пределения потоков и управления потоками в узлах? Как
отобразить параметры для конкретного узла? Покажите
на примере центральной вершины созданного графа.
6) Что определяют параметры вкладки "Распределение по-
токов"диалогового окна "Ввод параметров распределения
потоков в вершинах"? Имелись ли эти параметры в про-
грамме FlowNetworkA.exe?
34
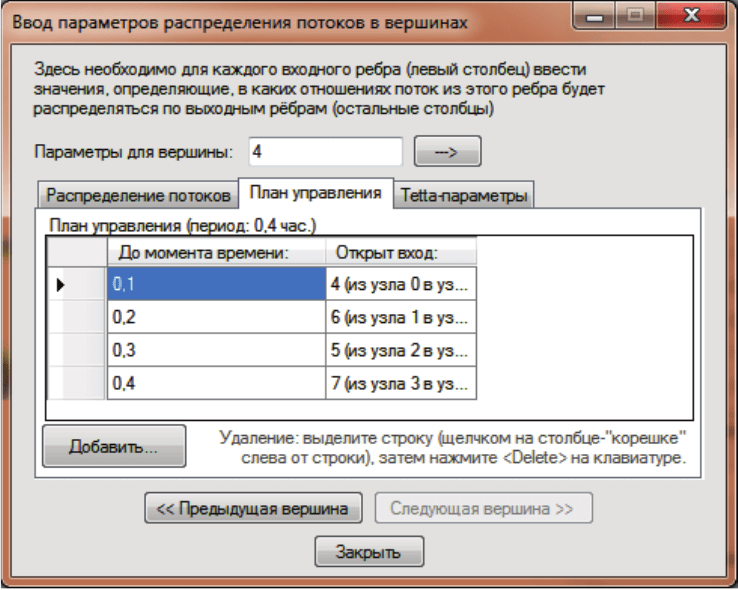
Рис. 33. Полностью сформированный план управления для узла №4
7) Опишите детально, что представляет собой план управ-
ления узла.
8) В приложении FlowNetworkB.exe: a) все узлы графа име-
ют план управления; б) могут быть как узлы с заданным
планом управления, так и узлы без него - какое утвер-
ждение верно?
9) В приложении FlowNetworkB.exe вновь создаваемые узлы
по умолчанию имеют или нет уже заданный план управ-
ления?
10) Определите план управления для центрального узла со-
зданного графа. Этот узел будет моделировать некоторый
перекресток со светофором. Пусть, например, светофор
будет открыт для каждого из входов в течение 0,05 ч.
11) Задайте некоторое начальное количество частиц (транс-
портных средств) для каждого ребра, после чего запу-
стите процесс моделирования. Как проявляется наличие
плана управления для центрального узла?
35
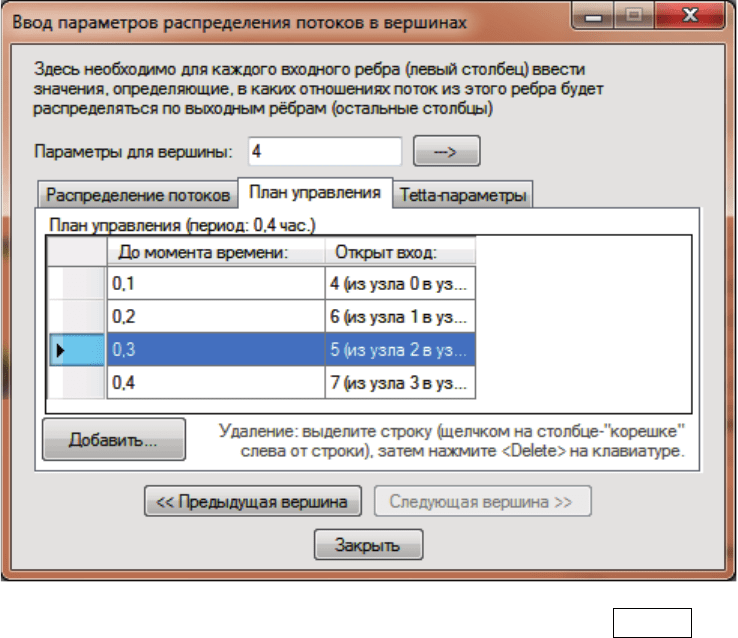
Рис. 34. Выделенную запись можно удалить, нажав Delete
3. Динамические системы на графах с управлением и
заторами. Пакет FlowNetworkC.exe
Пакет FlowNetworkC.exe разработан на основе пакета
FlowNetworkB.exe путем добавления к нему функций модели-
рования очередей перед узлами. Предыдущий пакет
FlowNetworkB.exe позволял моделировать движение материи
по графу и задавать планы управления в узлах; эти функции
полностью сохранены.
3.1. Теоретические основы
В методических указаниях по пакетам FlowNetworkA.exe
и FlowNetworkB.exe приводилось описание расчета движения
материи по ребрам. Но при этом не учитывалось возникно-
вение очередей, поскольку в предыдущих пакетах не было
возможности по моделированию очередей. Здесь описывают-
ся отличия, обусловленные наличием очередей.
Рассмотрим случай, когда на конечном узле ребра задан
план управления. То есть потоки, приходящие к этому узлу
со входящих в него ребер, в том числе и с данного ребра, про-
36
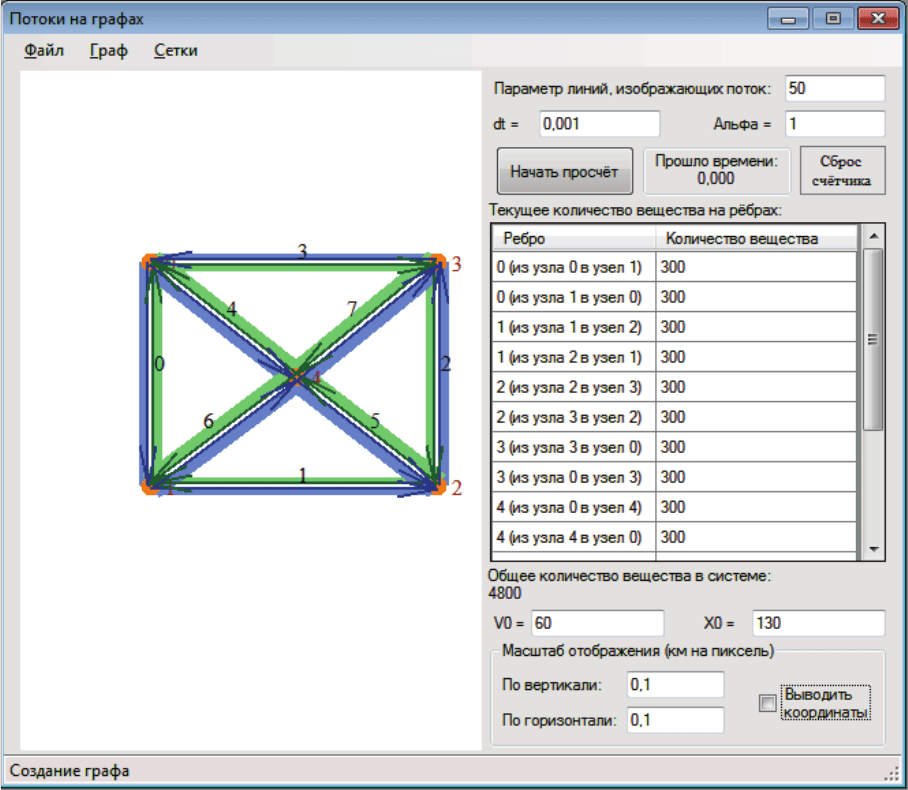
Рис. 35. Состояние модели в начале моделирования
ходят через узел попеременно: в течение какого-то времени
материя с одного ребра проходит через узел, распределяясь
по выходным ребрам, затем выход с этого ребра прекращает-
ся и начинается распределение материи со следующего ребра.
Таким образом, для ребра периодически возникает ситуация,
когда материя не выходит с него, а только накапливается на
нем. В предыдущем пакете (FlowNetworkB.exe) вся материя
на ребре всегда равномерно распределялась по длине ребра.
В данном пакете в случае, когда выход с ребра невозможен,
вблизи конечного узла ребра возникает очередь – область с
максимальной плотностью. Очередь растет, пока выход с реб-
ра закрыт, но существует приток материи к концу очереди.
К концу очереди материя подходит из той области ребра, на
которой движение еще свободное. Когда выход открывается,
очередь начинает уменьшаться.

37
Рис. 36. Состояние модели через некоторое время после начала моделирования
Каждое ребро характеризуется текущим количеством ве-
щества на нем. Кроме того, задается интенсивность s, с кото-
рой поток, выходящий из очереди, проходит через выходной
узел в случае если этот узел открыт для прохода. В данном
пакете величина s задается глобально для всего графа (будет
одинаковой для всех очередей). Если же очередь уже исчез-
ла, то поведение вещества на ребре будет аналогично тому,
как это было в предыдущем пакете. Поведение материи на
свободном участке ребра остается прежним. Интенсивность
рассчитывается так же, но вместо длины ребра и количества
вещества на ребре берется длина свободного участка и коли-
чество вещества на нем. Если очереди нет, то рассчитанная
интенсивность – это интенсивность, с которой материя со все-
го ребра приходит к конечному узлу. Если очередь есть, то
рассчитанная для свободной области ребра интенсивность –

38
Рис. 37. Колебательные изменения количества материи на ребрах
это интенсивность, с которой материя приходит к концу оче-
реди (т. е. пополняет очередь).
3.1.1. О потоках на транспортном цветке с управлением
Общая постановка
Транспортный цветок представляет собой плоский граф,
состоящий из n одинаковых ребер длины 1 с общей вершиной
(рис. 38).
Поток (движущаяся масса) на каждом ребре описывается
двумя параметрами (x
i
, ρ
i
) , i = 1, ..., n , где x
i
- длина части
i-ребра, на которой плоскость максимальна, ρ
max
= 1, ρ
i
-
плотность потока на оставшейся (1 − x
i
), примыкающей к x
i
по ходу движения.
Будем считать, что интенсивность свободного движения опре-
деляется классической основной диаграммой
f(ρ) = ρ (1 − ρ) , 0 ≤ ρ ≤ 1.

39
Рис. 38. Транспортный цветок
Движение через общую вершину осуществляется следую-
щим образом: в каждый момент времени открыто движение
через перекресток лишь одному контуру, т.е. θ
i
(t) , i = 1, ..., n
- функции со значением 0 и 1
θ
1
(t) + θ
2
(t) + ... + θ
n
(t) ≡ 1. (1)
Пусть A = ( a
ij
) - стохастическая квадратная матрица n×n,
a
ij
≥ 0 ,
n
∑
j=1
a
ij
= 1 , i = 1, ..., n. (2)
Таким образом, если θ
i
(t) = 1, то поток, поступающий в
вершину из i-контура, распределяется в соответствии с век-
тором (a
i1
, ...., a
in
), причем если x
i
(t) > 0, то интенсивность
поступления массы из i-контура в вершину положим посто-
янной S.
Следовательно, S - интенсивность убывания затора, а через
R обозначим пропускную способность узла.
Рассматриваемая динамическая система замкнута, посколь-
ку
n
∑
i=1
(x
i
· 1 + ρ
i
· (1 − x
i
)) ≡ const (3)
в качестве целевых функций, измерителей можно взять ра-
боту за определенный промежуток времени T , среднюю сум-
марную длину очередей (x
1
, ...., x
n
) , среднюю задержку и т.д.

40
Рис. 39. Динамика потока на ЭКР
В настоящей работе мы остановимся на частном случае, ко-
гда A = E, т.е. перемешивание потоков в узле отсутствует.
Задача об исследовании потоков на цветке сводится к иссле-
дованию потока на одном лепестке.
Поток на элементарном контуре с управлением
Рассмотрим задачу оптимизации потока на элементарном
контуре с регулированием (управлением) ЭКР (рис. 39),
S > f (ρ) ∀ρ.
Функция
Q (t) = (1 − x) f (ρ) + Sθ (t) x (4)
характеризует мощность потока на ЭКР в момент времени t.
Пусть x
0
= x (t
0
) , ρ
0
= ρ (t
0
) - состояние в начальный мо-
мент времени t
0
(t
0
< 0). Поскольку
˙x (t) =
{
−θ (t) S + f (ρ) , x > 0
(1 − θ (t)) f (ρ) , x = 0
(5)
(ρy)
·
t
=
{
θ (t) S − f (ρ) , x > 0,
− (1 − θ (t)) f (ρ) , x = 0,
(6)
то при θ (t) = 1 получаем
(1 − ρ (t)) (1 − x (t)) ≡ C, (7)
причем x (t) ↘. При θ (t) = 0 также справедливо (7) с одной
разницей, что x (t) ↗.
Таким образом, в фазовой плоскости имеем следующую
картину (рис. 40). Если x = x
0
, ρ = ρ
0
, то в соотношении
(7) C
0
= (1 − ρ
0
) (1 − x
0
).

41
Рис. 40. θ ≡ 1, (слева) θ ≡ 0
Периодические колебания
Пусть T — некоторый промежуток времени, (x
0
, ρ
0
) — на-
чальное состояние системы при t
0
= 0. Выберем на отрезке
[0,Т] такую точку T
1
, что при
θ (t) = {1, 0 < t < T
1
; 0, T
1
< t < T } (8)
система возвращается в исходное положение. Поскольку ди-
намика (x, ρ) при θ ≡ 1 и θ ≡ 0 монотонна и непрерывна, то
при фиксированном T существует единственное T
1
с требу-
емым условием, если T меньше времени движения из (x
0
, ρ
0
)
до границы и обратно, т.е. T достаточно мало.
3.1.2. Характеристики потока на элементарном контуре
Пусть (x, ρ ) — состояние потока на элементарном контуре
(см. рис. 39). Как уже отмечалось, характеристика
P (x, ρ, S, θ) = (1 − x) f (ρ) + Sθ (t) x (9)
описывает мощность потока (шт · м/сек).
Если [0, T ] некоторый промежуток времени, то величина
W =
T
∫
0
((1 − x (t)) f (ρ (t)) + Sθ (t) x (t)) dt (10)
описывает работу потока, и
P
∗
=
1
T
T
∫
0
Q (x (t) , ρ (t) , S, θ (t)) dt (11)
