Бояршинова А.К., Фишер А.С. Теория инженерного эксперимента. Текст лекций
Подождите немного. Документ загружается.

61
В ряде методик экспертных оценок предусматривается проведение нескольких
туров опроса. Это позволяет экспертам «взвесить» свои суждения с учетом отве-
тов и доводов коллег и дополнительной информации, которая не была учтена в
предыдущем туре. Выяснение причин, пусть даже недостаточно обоснованных,
но послуживших основой для суждений, приводит иногда к пересмотру от-
дельных оценок
.
Одним из интересных подходов к опросу и обобщению оценок, данных экс-
пертами, является метод Дельфы, получивший свое название от города Дельфы и
дельфийских мудрецов. Цель метода — составление тщательно скорректирован-
ной программы последовательных индивидуальных опросов, направленной на
уменьшение группового влияния, возникающего при совместной работе специа-
листов.
Основные принципы, положенные в основу
метода Дельфы, заключаются в
обеспечении анонимности опроса путем исключения непосредственного взаимо-
действия экспертов; при этом управляемая обратная связь устанавливается в виде
сообщения обработанной информации о согласованной точке зрения экспертов на
предыдущих этапах опроса. Обратная связь, регулируемая аналитиками, позволя-
ет выявить преобладающие суждения специалистов и сблизить их точки зрения на
проблему. Вместе
с тем, метод не имеет целью достижение полного единства
мнений, так как учитывается, что, несмотря на сближение точек зрения, раз-
личие будет существовать и в конце опроса.
Полагают, что благодаря письменной форме опроса экспертов снижается
влияние таких факторов, как внушение или приспособление к мнению большин-
ства.
Опрос производится в несколько
туров. Во время каждого тура экспер-
ты должны сообщить свое мнение и дать оценку ряда величин, например,
указать сроки свершения некоторых событий (изобретений, открытий, техни-
ческих достижений), которые должны, по их мнению, осуществиться в течение
прогнозируемого периода. После очередного тура опроса производится обработка
информации, полученной от экспертов. При этом за показатель
группового мне-
ния принимается медиана, а за показатель согласованности мнений — диапа-
зон квартилей, которые хорошо характеризуют совокупность полученной ин-
формации.
Предположим, что от экспертов получено какое-либо число оценок иссле-
дуемой величины, например, 11. Прежде всего эти оценки нужно расположить в
порядке их убывания. Затем необходимо найти медиану. В нашем примере
с 11
оценками она будет совпадать, как показано на рис. 6.1, с оценкой
6
N . Далее
нужно установить значения верхнего и нижнего квартилей
1
Q и
2
Q . Медиана и
квартили на оси ряда образуют четыре интервала, среди которых два средних
( MQ
1
и MQ
2
) считаются наиболее предпочтительными. Экспертов, чьи оценки
не лежат внутри диапазона квартилей
21
Q,Q
, просят обосновать причины расхож-
дения суждений и сообщить свое мнение по поводу совершенства постановки во-

62
просов. С их обоснованиями и выводами, не указывая от кого они получены, зна-
комят остальных экспертов.
Рис. 6.1. Медианы и квартили
Подобная процедура позволяет специалистам изменить в случае необходимо-
сти свою оценку, принимая в расчет обстоятельства, которые они могли слу-
чайно упустить или которыми пренебрегли в первом туре опроса. Благодаря это-
му результаты второго тура и последующих туров опроса дают, как правило,
меньший разброс оценок.
После получения оценок второго тура вновь производится процедура их упо-
рядочения и снова рассчитываются медиана и квартили. По результатам расчетов
аналитики подготавливают документ, в котором указывают (анонимно) основные
причины изменений оценок, происшедших во втором туре. В третьем и четвертом
турах все повторяется в той же последовательности, а медиана ответов последне-
го
тура принимается за обобщенное мнение.
Метод Дельфы позволяет получить более надежные оценки группового мне-
ния, чем в случае простого их усреднения. К недостаткам метода следует отнести
то, что взаимовлияние экспертов здесь полностью не исключено, так же как не
исключено и влияние «общественного» мнения на каждого из экспертов. Кроме
того, существует
значительная зависимость оценок, данных экспертами, от точ-
ности формулирования вопросов и аргументации.
6.3. Методы упорядочения альтернатив
Упорядочение – расположение объектов в порядке возрастания или убывания
какого-либо признака.
Методы упорядочения могут быть применены в следующих случаях.
1. Когда из общего числа альтернатив или каких-либо характерных признаков
(факторов, показателей) необходимо выделить наиболее важные.
В практике выбора альтернатив нередко случается, что одна из них превос-
ходит другие по одному
из показателей, в то время как другая лучше остальных
по какому-то другому показателю. Бывает, что эти показатели качественно раз-
личны или их нельзя соизмерить. В таких случаях выбирается какой-либо один
(или несколько) важный или значимый
показатель, на основе которого и про-
изводится выбор наиболее предпочтительной альтернативы.
2. Когда нужно сравнить некоторые количественные факторы, точные измере-
ния которых связаны со значительными трудностями.
11
N
1
N
2
N
6
N
5
N
4
N
3
N
7
N
8
N
9
N
10
N
2
Q
1
O
M
63
Упорядочение альтернатив или факторов при решении сложных задач может
служить способом, позволяющим в короткие сроки получить приближенный ответ.
3. Когда
необходимо оценить какие-либо качественные факторы, которые
нельзя точно измерить, но можно сопоставить степень обладания каждого из них
этим качеством.
В повседневной жизни мы часто оцениваем такие факторы с помощью
слов: «лучше», «ценнее», «полезнее», «красивее», «талантливее» и т. д.
Наиболее распространенными методами упорядочения альтернатив (факторов,
показателей) являются: 1) ранжирование; 2) непосредственная оценка; 3)
после-
довательное сравнение и 4) парное сравнение.
Ранжирование — процедура установления относительной значимости (пред-
почтительности) исследуемых объектов на основе их упорядочения. Ранг — это
показатель, характеризующий порядковое место оцениваемого объекта или явле-
ния в группе других объектов (явлений), обладающих существенными для оценки
свойствами. Обычно наиболее предпочтительному объекту присваивается первый
ранг, а наименее предпочтительному —
последний.
Точность и надежность ранжирования в значительной степени зависят от ко-
личества объектов. В принципе чем таких объектов меньше, тем выше их
«различимость» с точки зрения эксперта и тем надежнее можно установить ранг
объекта.
Итак, при ранжировании эксперт должен расположить объекты (факторы, аль-
тернативы) в порядке, который представляется ему наиболее
рациональным, и
приписать каждому из них числа натурального ряда: 1, 2, 3 и т. д.
Следовательно, порядковая шкала, получаемая в результате ранжирования,
должна удовлетворять условию равенства числа рангов числу ранжированных
объектов.
Бывает так, что эксперт не в состоянии указать порядок следования двух или
нескольких объектов либо он разным объектам присваивает один и тот же
ранг, и
в результате число рангов N оказывается не равным числу ранжируемых объектов
п. В таких случаях объектам приписываются так называемые стандартизирован-
ные ранги. С этой целью полагают общее число рангов равным п, а объектам,
имеющим одинаковые ранги, присваивается стандартизированный ранг, значение
которого равно среднему суммы мест, поделенных между собой объектами
с оди-
наковыми рангами.
Когда ранжирование производится несколькими экспертами, сначала подсчи-
тывается сумма рангов для каждого объекта, причем, наивысший (первый) ранг
присваивается объекту, получившему наименьшую сумму рангов, и, наоборот,
объекту с наибольшей суммой рангов присваивается самый низкий ранг N. Ос-
тальные объекты упорядочиваются в соответствии со значением суммы ран-
гов относительно
объекта, которому присвоен первый ранг. Рассмотрим пример
ранжирования факторов несколькими экспертами.
Представим, что три эксперта должны ранжировать три основных фактора,
влияющих на оценку предпочтительности альтернатив, и что этими факторами
являются: техническая новизна, ожидаемая прибыль и срок освоения.
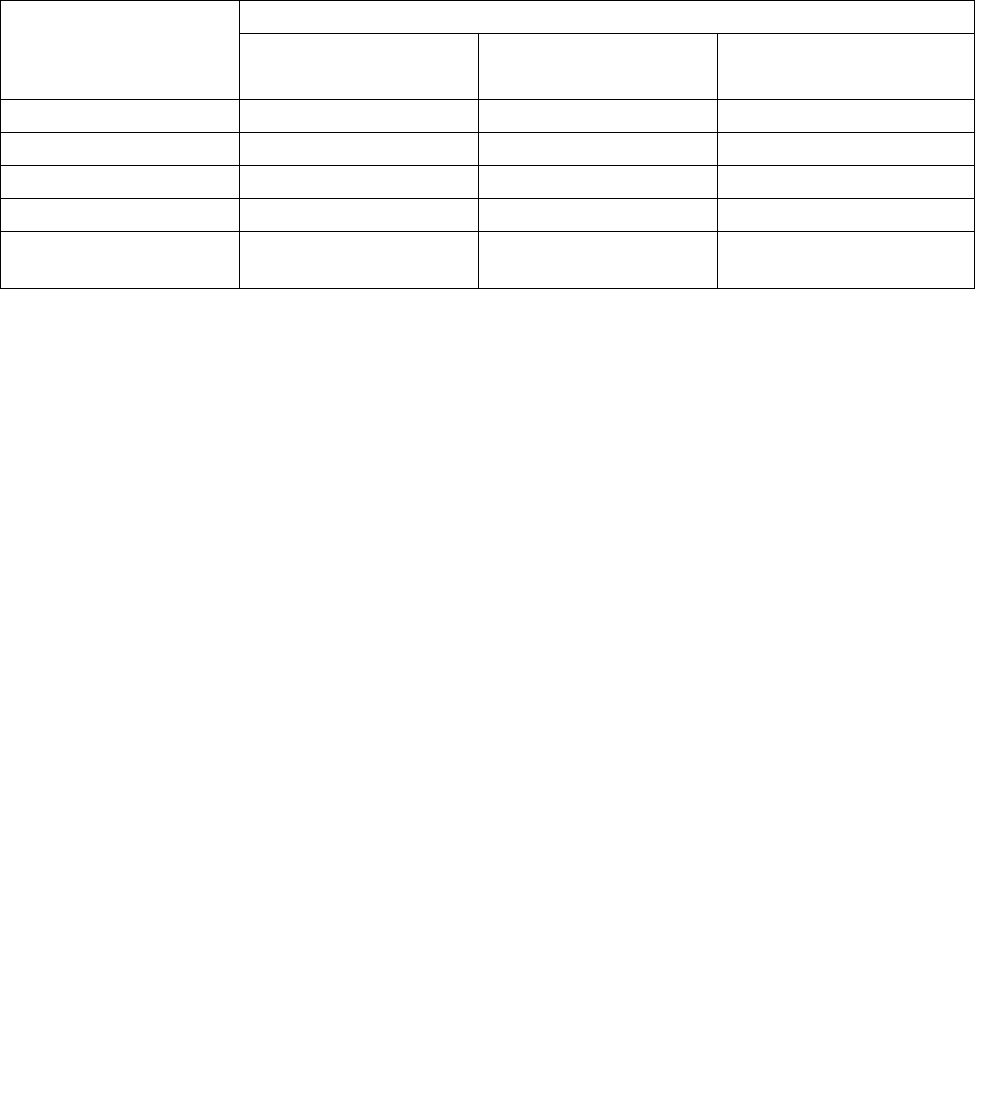
64
Предположим, что каждому из факторов эксперты присвоили соответствую-
щие ранги, показанные в первых трех строках табл. 6.1.
Как видно из таблицы, в этом случае наивысший (I) результирующий ранг
присваивается фактору, получившему наименьшую сумму рангов, т. е. наиболь-
шее число первых мест. Последующие ранги (II и III) устанавливаются в зависи-
мости от порядка суммы рангов, полученной
другими факторами.
Таблица 6.1
Определение результирующего ранга
Факторы
Эксперты
техническая но-
визна
ожидаемая при-
быль
срок освоения
Иванов
1 2 3
Петров
2 1 3
Сидоров
1 3 2
Сумма рангов
4 6 8
Результирующий
ранг фактора
I II III
Следует отметить, что ранг определяет лишь место, занимаемое объектом
среди других объектов в отношении какого-то важного для анализа свойства
или качества. На вопрос о том, как далеко отстоят друг от друга исследуемые
объекты, метод ранжирования ответа не дает.
На практике метод ранжирования «в чистом виде» используется редко. Чаще
всего он применяется в сочетании с другими методами упорядочения, обеспе-
чивающими более четкую различимость сравниваемых объектов.
Так, ранжирование может быть использовано в сочетании с методом непо-
средственной оценки. Для этого разрабатывается шкала, каждому интервалу ко-
торой присваивается оценка (балл), например, от 1 до 10. Величины интервалов
должны быть, с точки зрения экспертов, равными.
При сравнении альтернатив с помощью метода последовательных сравнений
проводится следующая процедура:
1) альтернативы располагаются в порядке их важности (как и при ранжиро-
вании);
2) наиболее важной альтернативе приписывается оценка
1
v равная еди-
нице, а остальным (соответственно степени их важности) — оценки
i
v между
нулем и единицей;
3) решается, будет ли альтернатива с оценкой 1 превосходить по важности
все остальные альтернативы, взятые вместе. Если да, то оценка этой альтерна-
тивы
1
v увеличивается так, чтобы выполнялось условие
,vv
n
i
i
∑
=
>
2
1

65
где
i
v – оценки всех остальных альтернатив. В противном случае величина
1
v
изменяется так, чтобы было справедливо неравенство
∑
=
<
n
i
i
vv
2
1
;
4) определяется, будет ли вторая по важности альтернатива с оценкой
2
v
бо-
лее важна, нежели все последующие с более низкими оценками; затем проводит-
ся та же процедура, что и с оценкой
1
v ;
5) эта процедура продолжается до тех пор, пока не будет оценена
(
)
1
−
n -ая
альтернатива (фактор).
При наличии большого числа альтернатив (более семи) применение метода
последовательных сравнений становится чрезмерно трудоемким. Тогда для оп-
ределения предпочтительности альтернатив обычно используется метод парных
сравнений, суть которого состоит в следующем.
Предлагается произвести сравнение альтернатив (или факторов) попарно, с
тем, чтобы установить наиболее значимую в каждой такой паре.
Для проведения этой процедуры составляют специальную таблицу — мат-
рицу парных сравнений (табл. 6.2). Здесь все сопоставляемые факторы запи-
сываются в одном и том же порядке дважды: в верхней строке и в левом
крайнем столбце.
Каждый эксперт, заполняющий такую матрицу, должен проставить на
пересечении сравниваемых факторов оценку
qp
x. Причем, если фактор q бо-
лее предпочтителен, чем фактор
p
, эта оценка равна 1; если наоборот, то
оценка равна 0.
В случаях, когда каждая пара факторов сравнивается однократно, число
сравнений будет
(
)
2
1
−
=
nn
I , (6.5)
где n – общее число факторов.
Если, например, имеется 4 альтернативы, то каждый эксперт должен произ-
вести
(
)
6
2
144
4
=
−
=I
сравнений.
Часть матрицы парных сравнений, лежащая ниже главной диагонали, запол-
няется в соответствии с проставленными оценками по каждой сравниваемой паре
факторов [8, 9].
Складывая построчно проставленные оценки, получаем для каждого фактора
частоту предпочтений
j
ω
, где ,n...,,j 1
=
и затем по полученным частотам пред-
почтений можно проставить ранги показателей.
Для примера в таблице 6.3 представлена заполненная экспертом матрица пар-
ных сравнений показателей назначения автотранспортного средства. Для опреде-
ления весовых коэффициентов показателей определяется суммарная частота

66
предпочтений i -го показателя для всех
M
опрошенных экспертов:
∑
=
ω=ω
M
j
iji
1
,
где n...,,i 1= .
Таблица 6.2
Матрица парных сравнений
1 2
…
p
…
n
1
2
.
.
.
q
.
.
.
n
–
21
x
.
.
.
1q
x
.
.
.
1n
x
12
x
–
.
.
.
2q
x
.
.
.
2n
x
p
x
1
p
x
2
.
.
.
qp
x
.
.
.
np
x
n
x
1
n
x
2
qn
x
.
.
.
–
Весовые коэффициенты рассчитывают по формуле
MJ
m
i
i
ω
= . (6.6)
Определять весовые коэффициенты таким образом имеет смысл, если мнения
опрошенных экспертов согласованы. Степень согласованности мнений экспертов
можно оценить по так называемому коэффициенту конкордации W . Расчет ко-
эффициента конкордации осуществляется по формуле
()
∑
∑
=
=
−−
=
M
j
j
n
i
i
TnnM
d
W
1
32
1
2
12
, (6.7)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
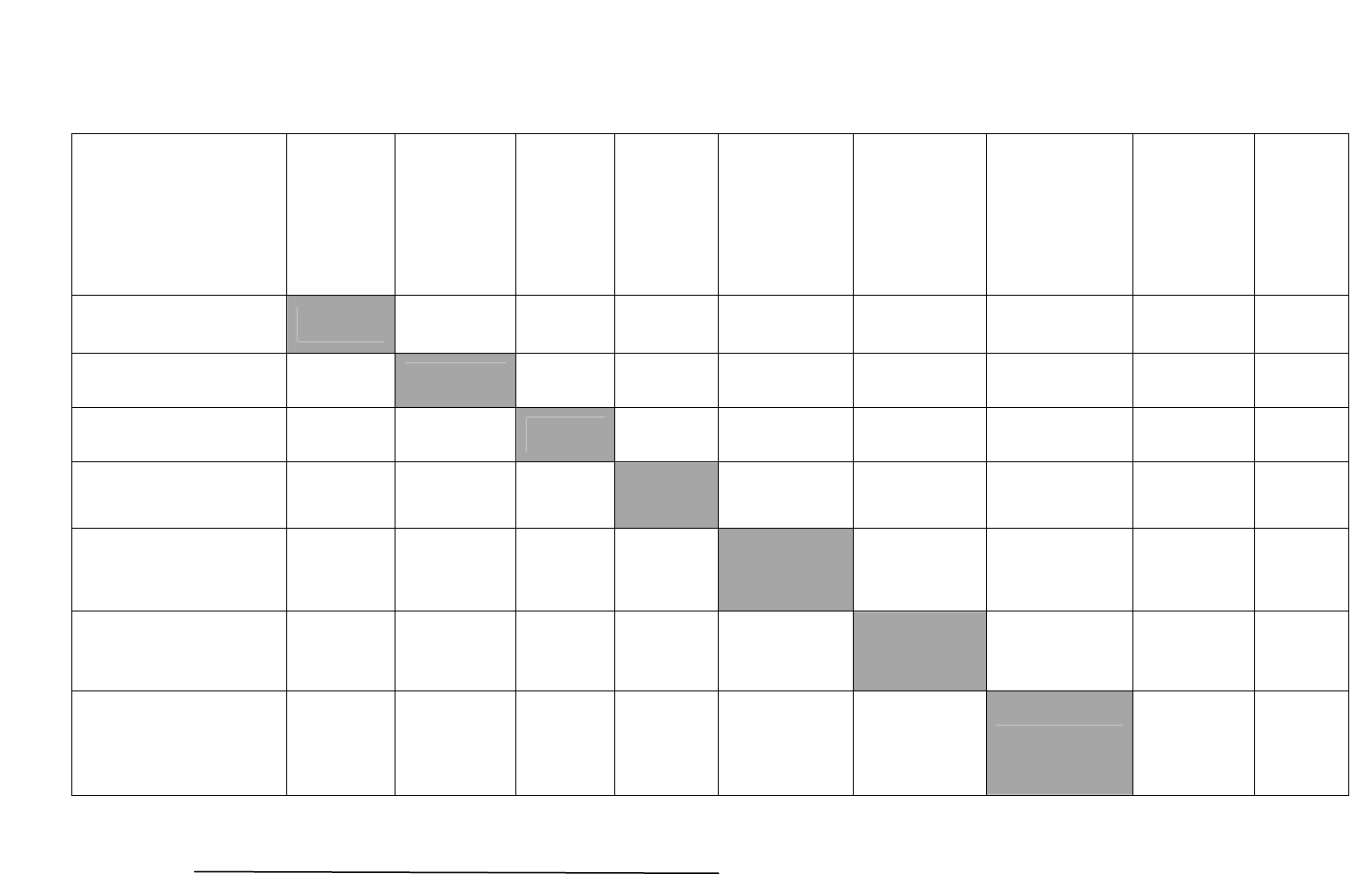
Наименование
показателя
Мощ-
ность
двигате-
ля
Макси-
маль-ная
скорость
Время
разгона
до 60
км/ч
Наи-
мень-
ший ра-
диус
поворо-
та
Наимень-
ший до-
рожный
просвет
Тормозной
путь при
начальной
скорости
60 км/ч
Максималь-
ный подъем
при движе-
нии с пол-
ной нагруз-
кой
Частота
предпоч-
тения по-
казателя
Ранг
Мощность двигателя
1 1 0 0 0 0
2 5
Максимальная ско-
рость
0
0 0 0 0 0
0 7
Время разгона до 60
км/ч
0 1
0 0 0 0
1 6
Наименьший радиус
поворота
1 1 1
1 1 1
6 1
Наименьший дорож-
ный просвет
1 1 1 0
1 1
4 2,5
Тормозной путь при
начальной скорости 60
км/ч
1 1 1 0 0
1
4 2,5
Максимальный подъем
при движении с полной
нагрузкой
1 1 1 0 0 0
3 4
Таблица 6.3
Матрица парных сравнений показателей назначения
67
Эксперт: Середа В.А., МУП «ЧПАТО-2», начальник ОЭ
Ф.И.О., место работы, должность

68
где n – число факторов (показателей);
i
d – отклонение суммы рангов
i
-го показа-
теля, вычисленной по всем экспертам от средней арифметической сумм рангов n
показателей;
(
)
jjj
ttT −=
3
– показатель равных рангов,
j
t – число равных рангов,
проставленных
j
-ым экспертом. Будем считать, что при
50W ,<
мнения экспер-
тов значительно расходятся и результатами такого опроса пользоваться нельзя.
Пример расчета коэффициента конкордации приведен в таблице 6.4.
Подставив полученные значения в формулу (6.7), получим
()
375,0
6223
5,112
32
=
−−
⋅
=W .
Вывод: мнения экспертов не согласованны.
Таблица 6.4
Ранги по факторам
Эксперты
техничес-
кая новизна
ожидае-
мая при-
быль
срок ос-
воения
Число
равных
рангов
i
t
Показа-
тель рав-
ных ран-
гов
j
T
Иванов
Петров
Васильев
2,5
3
1
1
2
2
2,5
1
3
2
0
0
6
Сумма рангов
j
S
Средняя арифметиче-
ская
ср
S
jсрj
SSd −=
2
j
d
6,5
6
–0,5
0,25
5
1
1
6,5
–0,5
0,25
∑
=
M
j
j
a
1
2
M
n
∑
=
M
j
j
T
1
1,5
3
3
6
6.4 . Методика анализа потребительских свойств
автотранспортных средств с применением
экспертных методов
Анализ потребительских свойств автотранспортных средств (АТС) основан на
сравнении обобщенных показателей потребительских свойств.
69
Для проведения работы по сравнительному анализу потребительских свойств
АТС на предприятии из числа квалифицированных работников высшего звена
(ИТР) формируется так называемая рабочая группа.
Этапы деятельности рабочей группы следующие.
1.
Выбор альтернативных моделей АТС одного класса.
2.
Определение наименований групп показателей и показателей потребитель-
ских свойств по группам.
3.
Определение значений показателей для всех моделей АТС по соответст-
вующей справочной литературе, технической документации и т.д.
4.
Подбор экспертных групп для определения балльных оценок показателей,
коэффициентов весомости показателей и групп показателей.
5.
Расчет обобщенных показателей потребительских свойств выбранного мо-
дельного ряда АТС.
6.
Выводы и рекомендации.
Для определения балльных оценок показателей какой-либо группы (эргономи-
ческих показателей салона автобуса, эстетических показателей и т. п.) задается
система балльных оценок (например, пятибалльная), и каждый эксперт оценивает
в баллах указанные в анкете показатели для предложенного модельного ряда
АТС. Пример анкеты для индивидуального опроса показан на рис. 6.2. По
запол-
ненным анкетам необходимо убедиться в согласованности мнений экспертов. При
низкой степени согласованности мнений рабочая группа должна выработать так-
тику по сближению оценок (выявление причин несогласованности, беседы с экс-
пертами, использование метода Дельфы и т. д.). При достаточной степени совпа-
дения мнений экспертов согласованные балльные оценки показателей определя-
ются как
среднеарифметические для каждого показателя по всем анкетам.
Для определения весовых коэффициентов группа экспертов формируется из
числа ведущих специалистов автотранспортных предприятий, а также высококва-
лифицированных специалистов в области автомобильного транспорта городского
и областного уровней. Численность экспертных групп составляет 8 – 10 человек.
Опрос экспертов проводится по анкетам, составленным в виде матрицы парных
сравнений. Анализ согласованности
мнений экспертов проводится на основе рас-
чета коэффициентов конкордации W по каждой группе показателей и по группам
показателей.
Определение весовых коэффициентов показателей и групп проводится по-
сле согласования мнений экспертов по методике, изложенной в п. 6.3.

70
Анкета
Сравнительные балльные оценки показателей группы “Эргономические
показатели салона автобуса”
Марка автобуса
Показатели
«УВЕЛЬКА» ПАЗ-3205 ЗИЛ-3250
1
Удобство расположения органов
управления
3 4 5
2
Обзорность дороги с места води-
теля
4 4 3
3
Самочувствие водителя в течение
рабочего времени
4 3 4
4 Удобство сиденья 3 4 4
Примечание: использовать пятибалльную систему.
Анкету заполнил:
Ф.И.О. Фалолеев Н.А.
Место работы МУП “ППТП-2”
Должность водитель
Рис. 6.2. Пример анкеты для получения бальных оценок показателей
6.5. Расчет обобщенных показателей потребительских
свойств автобусов
Расчет обобщенных показателей потребительских свойств АТС рассматривае-
мого ряда моделей выполняется по стандартной методике.
1. Выбор базовой модели АТС.
Выбор базового АТС произволен и не влияет на результат расчета обобщен-
ных показателей потребительских свойств АТС.
2. Расчет относительных показателей
i
g .
Показатели рассматриваемых моделей АТС сравниваются с соответствующи-
ми показателями модели, принятой за базовую. При этом, если значение показа-
теля g
i
(i=1,…,n, где n – число показателей) модели лучше соответствующего зна-
чения
б
i
g базовой модели, то значение относительного показателя
i
g должно быть
