Бояршинова А.К., Фишер А.С. Теория инженерного эксперимента. Текст лекций
Подождите немного. Документ загружается.

11
Рис.2.2. Опыты полного двухфакторного эксперимента
Таблица 2.3
Полный трехфакторный эксперимент
Матрица планирования полного факторного эксперимента обладает следую-
щими свойствами:
1.
0
1
=∑
=
ji
N
j
X ; (2.10)
Факторы
Номер
опыта
1
X
2
X
3
X
Функция
отклика
1
−1 −1 −1
э
y
1
2 +1
−1 −1
э
y
2
3
−1
+1
−1
э
y
3
4 +1 +1
−1
э
y
4
5
−1 −1
+1
э
y
5
6 +1
−1
+1
э
y
6
7
−1
+1 +1
э
y
7
8 +1 +1 +1
э
y
7
2
X
1
X
0
3
2
–1
+1
+1
–1
1
4
12
2. NX
ji
N
j
=∑
=
2
1
; (2.11)
3.
0
1
=∑
=
jmjl
N
j
XX , (2.12)
где
m
l
≠ , N – число опытов; j – номер опыта; i, l, m – номера факторов.
Свойство, выраженное уравнением (2.12), называется ортогональностью. По-
этому говорят, что матрица полного факторного эксперимента ортогональна. Это
свойство позволяет вычислять коэффициенты регрессии по простым формулам
независимо друг от друга.
Общее количество опытов в матрице планирования
n
N
2
=
,
где
n – число факторов. (2.13)
На основании ПФЭ вычисляют коэффициенты регрессии, пользуясь следую-
щими формулами:
j
N
j
y
N
b
1
0
1
=
∑=
;
jji
N
j
i
yX
N
b
1
1
=
∑= ;
jjmjl
N
j
lm
yXX
N
b
1
1
=
∑=
,
где
m
l
≠
.
Благодаря кодированию факторов расчет коэффициентов превратился в про-
стую арифметическую процедуру (для расчетов используются соответствующие
вектор-столбцы).
Так, для полного двухфакторного эксперимента уравнение регрессии имеет
вид
211222110
XXbXbXbby
+
+
+
=
.
По таблице 2.2 находим коэффициенты:
.)1)(1()1)(1()1)(1()1)(1(
,)1()1()1()1(
,)1()1()1()1(
,
432112
43212
43211
43210
ээээ
ээээ
ээээ
ээээ
yyyyb
yyyyb
yyyyb
yyyyb
++++−+−++−−=
++++−+−+
++−+++−+
+++=
Значения коэффициентов указывают на силу влияния факторов на функцию
цели.
(2.14)

13
Некоторые из коэффициентов регрессии могут оказаться пренебрежимо ма-
лыми – незначимыми. Для установления факта незначимости коэффициента не-
обходимо вычислить оценки дисперсии, с которой они определялись:
Nk
S
S
воспр
в
2
2
=
, (2.15)
где
∑
=
22
1
jвоспр
S
N
S , k – число параллельных опытов.
С оценками дисперсий
2
воспр
S
и
2
в
S
связывают число степеней свободы:
)1(
−
=
kNf
воспр
. (2.16)
Принято считать, что коэффициент регрессии значим, если выполнено условие
n,в
tSв
α
⋅
≥ , (2.17)
где
n,
t
α
– значение критерия Стьюдента, которое находят по таблицам (см. При-
ложение 2).
Здесь индекс
α
− заданная доверительная вероятность;
(
)
1
−
== kNfn
воспр
.
В противном случае коэффициент незначим, и соответствующий член можно
исключить из уравнения регрессии.
Далее следует проверить адекватность полученного уравнения регрессии.
Под адекватностью в данном случае понимают способность построенной ма-
тематической модели соответствовать результатам эксперимента с заданной сте-
пенью точности. Эту проверку осуществляют с помощью критерия Фишера
2
2
воспр
ад
р
S
S
F =
, (2.18)
где
2
ад
S
− оценка дисперсии адекватности,
)1(
)(
1
2
2
+−
−
=
∑
=
nN
уyk
S
N
j
p
j
э
j
ад
; (2.19)
p
j
э
j
yy ,
− экспериментальные и расчетные значения функции отклика в j-ом опы-
те; N
−
число опытов ПФЭ; n
−
число факторов; k
−
число параллельных опытов.
С дисперсией адекватности (2.19) связывают число степеней свободы:
)1(
+
−
=
nNf
ад
. (2.20)
По таблицам для критерия Фишера (Приложение 3), зная
воспр
f
и
ад
f , опреде-
ляют табличное значения
Т
F
.
Уравнение регрессии считается адекватным, если выполняется условие
Tp
FF
≤
. (2.21)
14
Функция цели у найдена для кодированных факторов; чтобы перейти к реаль-
ным факторам, достаточно сделать подстановку
i
ii
i
x
xx
X
∆
−
=
0
,
где
iii
xxx ∆,,
0
– значения соответствующего реального фактора.
2.6. Метод дробных реплик
С увеличением количества факторов резко возрастает количество опытов пол-
ного факторного эксперимента. Это видно из уравнения
N=2
n
. Однако для нахож-
дения коэффициентов регрессии не всегда требуется много опытов. В таких слу-
чаях можно уменьшить объем экспериментальных работ, воспользовавшись ме-
тодом дробных реплик
.
Рассматриваемый метод заключается в том, что для нахождения математиче-
ского описания процесса используется определенная часть полного факторного
эксперимента: 1/2, 1/4 и т. д. Эти системы опытов называются дробными репли-
ками (табл. 2.4).
Таблица 2.4
Полный трехфакторный эксперимент и его дробные реплики
Факторы
Номер
опыта
X
1
x
2
x
3
Функция
отклика
Дробные
Реплики
1
2
3
4
5
6
7
8
−1
+1
−1
+1
−1
+1
−1
+1
−1
−1
+1
+1
−1
−1
+1
+1
−1
−1
−1
−1
+1
+1
+1
+1
y
1
y
2
y
3
y
4
y
5
y
6
y
7
y
8
2
1
Расчет коэффициентов регрессии, проверка значимости коэффициентов и аде-
кватности математического описания в данном случае производятся так же, как и
при полном факторном эксперименте.
Пусть, например, требуется найти коэффициенты уравнения регрессии
3322110
XbXbXbby
+
+
+
=
.
Здесь четыре неизвестных коэффициента.
Если для их определения воспользоваться полным трехфакторным экспери-
ментом, то необходимо провести 8 опытов. Однако эту задачу можно решить и с
помощью меньшего количества опытов.
¼
¼
¼
¼
2
1
15
Например, возьмем матрицу полного двухфакторного эксперимента (табл.2.5)
и приравняем произведение
X
1
X
2
к фактору X
3
.
Пользуясь формулой (2.14), вычислим:
)(
4
1
43210
yyyyb +++=
,
)(
4
1
43211
yyyyb +−+−=
,
)(
4
1
43212
yyyyb ++−−=
.
Таблица 2.5
Планирование типа 2
3−1
Номер
опыта
X
1
X
2
X
1
X
2
X
3
Функция
отклика
1
2
3
4
−1
+1
−1
+1
−1
−1
+1
+1
+1
−1
−1
+1
+1
−1
−1
+1
y
1
y
2
y
3
y
4
Отметим, что в табл. 2.5 столбцы для произведения X
1
X
2
и фактора X
3
полно-
стью совпадают. Поэтому коэффициенты b
12
и b
3
не могут быть определены раз-
дельно. С помощью формулы (2.14) может быть найдена только их сумма:
)(
4
1
4321312
yyyybb +−−=+
.
Этот недостаток рассматриваемого плана является своеобразной «платой» за
уменьшение общего количества опытов с восьми до четырех.
Такое планирование эксперимента, когда некоторые из факторов приравнива-
ют к произведениям нескольких факторов, называется планированием со смеши-
ванием
. Его обозначают символом 2
n
−
p
, где n – общее число факторов, а р – число
факторов, приравненных к произведениям. С этой точки зрения в табл. 2.5 приве-
дена матрица планирования типа 2
3−1
.
Существует правило, позволяющее определить, какие коэффициенты регрес-
сии определяются совместно при планировании со смешиванием. Рассмотрим это
правило на конкретном примере.
Пример. Методом дробных реплик будем искать математическое описание
процесса в виде уравнения регрессии:
55443322110
XbXbXBXbXbby
+
+
+
+
+=
.
Воспользуемся планированием типа 2
5−2
и примем:
214
XXX
−
=
;
3215
XXXX
=
.
16
Такие равенства в методе дробных реплик называют генерирующими соотно-
шениями.
Следует отметить, что выбор генерирующих соотношений в общем случае
произволен. Однако он существенно влияет на характер совместных оценок ко-
эффициентов регрессии.
Правило определения совместных оценок коэффициентов состоит в следую-
щем.
1. Примем во внимание, что
1
2
=
i
X
;
ii
XX
=
⋅
1.
2. Умножив обе части генерирующих соотношений соответственно на
X
4
и X
5
,
получим:
421
1 XXX
−
=
;
5321
1 XXXX
=
.
Эти равенства называют определяющими контрастами. Перемножив их по-
членно, получим новые
определяющие контрасты. В данном случае это
543
1 XXX
−
=
.
3. Составим алгебраическую сумму из единицы и правых частей всех полу-
ченных определяющих контрастов:
5435321421
1 XXXXXXXXXXS
−
+
−= .
4. Умножив каждый из факторов на S и заменив факторы соответствующими
коэффициентами разложения в ряд Тейлора (2.5), получим:
13452352411
β
β
β
β
−
+
−
→b
;
23451351422
β
β
β
β
−
+
−
→b
;
45125123433
β
β
β
β
−
+
−
→b ;
35123451244
β
β
β
β
−
+
−
→b ;
34123124555
β
β
β
β
−
+
−
→b .
2.7. Метод ортогонального центрального композиционного
планирования
В том случае, когда поверхность отклика не может быть описана многочленом
вида (2.9), для адекватного математического описания используется многочлен
более высокой степени
, например, отрезок ряда Тейлора (2.5), содержащий члены
с квадратами переменных. С этой целью используют центральное композицион-

17
ное планирование эксперимента (ЦКП). Различают два вида ЦКП: ортогональное
и ротатабельное.
Количество опытов при ортогональном ЦКП определяется по формуле
122 ++= n
n
N
, (2.22)
где 2
n
– количество опытов, образующих полный факторный эксперимент;
2
n – число так называемых «звездных» точек в факторном пространстве, имею-
щих координаты (±
α, 0, 0, ..., 0); (0, ±α, 0, ..., 0), ..., (0, 0, ..., ±α). Здесь величина
α
называется «звездным» плечом; 1 – опыт в центре планирования, т. е. в точке
факторного пространства с координатами (0, 0, ..., 0).
Если с помощью полного факторного эксперимента не удается получить адек-
ватного математического описания в форме (2.9), то к нему добавляют опыты в
«звездных» точках и в центре плана, а полученную при этом композицию
исполь-
зуют для получения математического описания процесса в виде многочлена вто-
рой степени. Отсюда и произошло название метода: центральное композиционное
планирование.
Значения «звездного» плеча
α для ЦКП с различным числом факторов п сле-
дующие:
n 2 3 4 5
α
1,000 1,215 1,414 1,547
Эти значения
α выбраны из условия ортогональности матрицы планирования.
Уравнение регрессии при ортогональном ЦКП ищут в следующем виде:
....
......
**
111
1)1(21122211
*
0
nnn
nnnnnn
XbXb
XXbXXbXbXbXbby
+++
++++++++=
−−
(2.23)
Переменные величины
∑
=
∗
−=
N
j
jijiji
X
N
XX
1
22
1
(j – номер опыта; i – номер фактора) (2.24)
введены для того, чтобы матрица планирования была ортогональна и коэффици-
енты регрессии определялись независимо друг от друга по результатам опытов.
Для того, чтобы получить уравнение регрессии в обычной форме
,...
......
22
222
2
111
1)1(211222110
nnn
nnnnnn
XbXbXb
XXbXXbXbXbXbby
++++
+
+
+
+
+
+
+
+
=
−−
(2.25)
находят величину
....
1
2
1
2
11
*
00
∑
−−
∑
−=
==
N
j
jn
nn
N
j
ji
X
N
b
X
N
b
bb (2.26)
В табл. 2.6. приведена в качестве примера матрица ортогонального ЦКП для
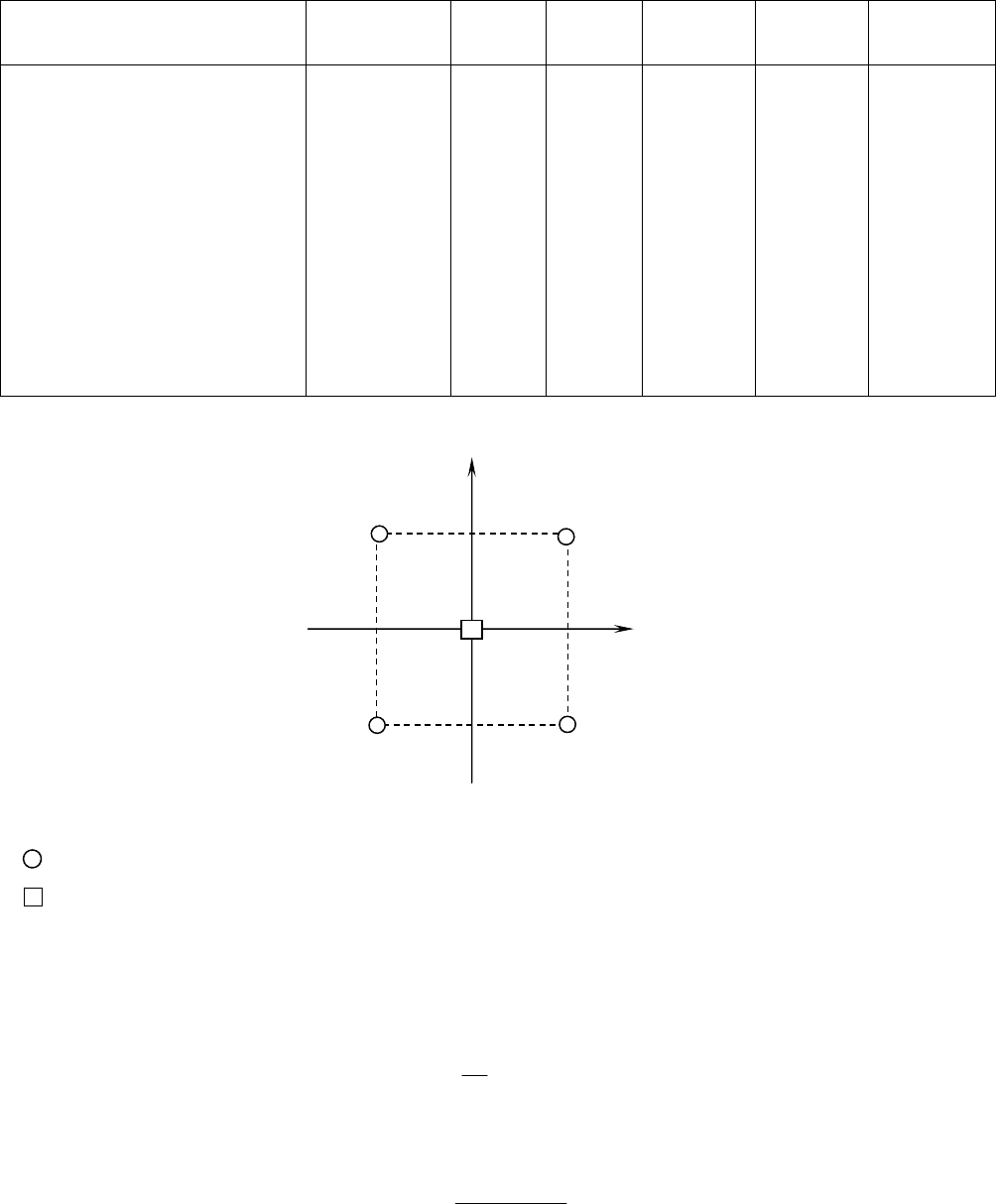
двух факторов, а на рис. 2.3 изображена схема этих опытов.
18
Таблица 2.6
Ортогональное ЦКП для двух факторов
Система опытов
Номер
опыта
X
1
X
2
X
1
X
2
X
1
*
X
2
*
Полный
факторный
эксперимент
Опыты
в звездных
точках
Опыт в центре плана
1
2
3
4
5
6
7
8
9
−1
−1
−1
−1
+1
−1
0
0
0
−1
−1
+1
+1
0
0
+1
−1
0
+1
−1
−1
+1
0
0
0
0
0
+0,33
+0,33
+0,33
+0,33
+0,33
+0,33
−0,67
−0,67
−0,67
+0,33
+0,33
+0,33
+0,33
-0,67
-0,67
+0,33
+0,33
−0,67
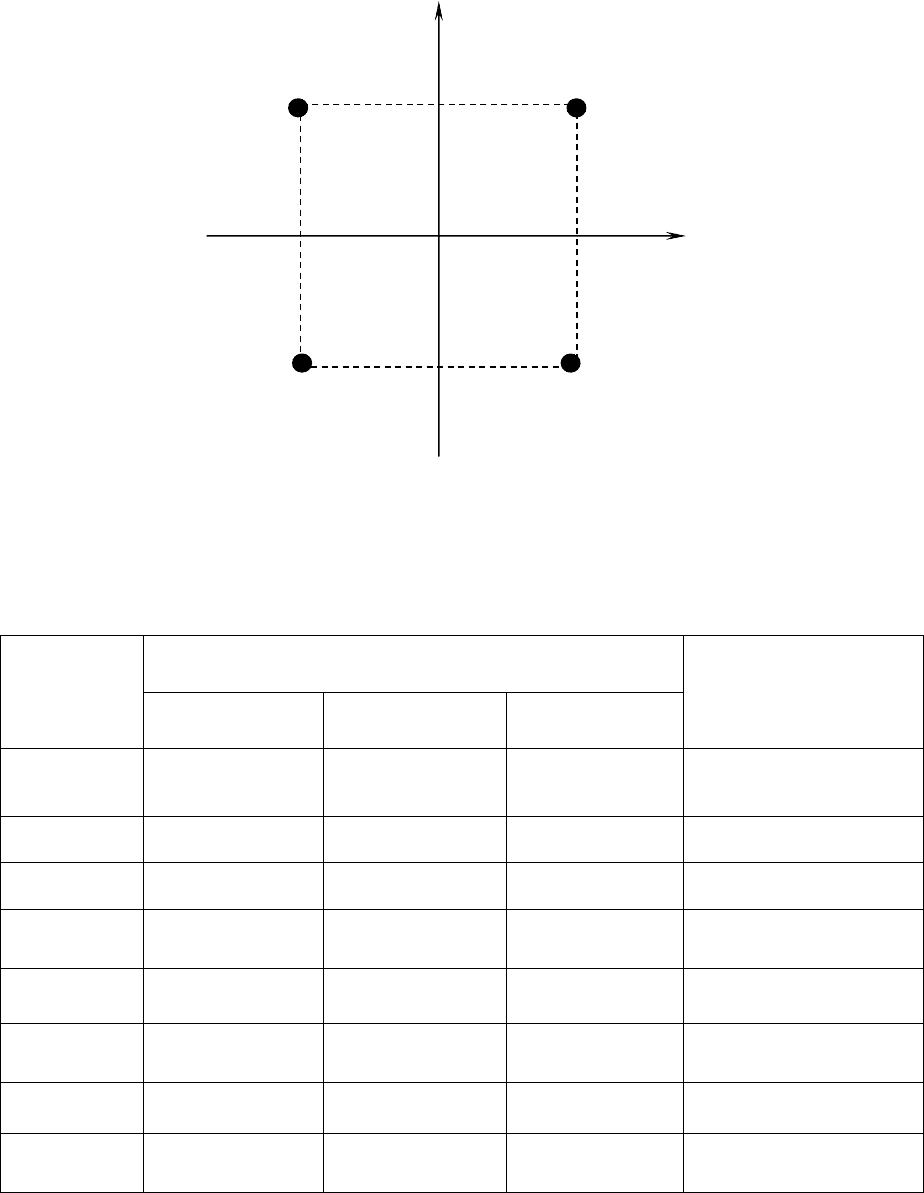
Рис.2.3. Схема опытов ортогонального ЦКП для двух факторов:
–
опыты полного факторного эксперимента; * – опыты в звездных точках;
– опыт в центре плана
Коэффициенты регрессии при ортогональном ЦКП рассчитываются по сле-
дующим формулам:
∑
=
=
N
j
j
y
N
b
1
*
0
1
, (2.27)
∑
∑
=
=
=
N
j
ji
N
j
jji
i
X
yX
b
1
2
1
)(
(где i≠0), (2.28)
1
X
2
X
+1
–1
–1
+1
*
*
*
*

19
∑
∑
=
=
=
N
j
jkji
N
j
j
k
jji
ik
XX
yXX
b
1
2
1
)(
(где i≠k ), (2.29)
∑
∑
=
=
=
N
j
ji
N
j
jji
ii
X
yX
b
1
2*
1
*
)(
. (2.30)
Для расчета оценок дисперсий в определении коэффициентов регрессии ис-
пользуют следующие выражения:
N
S
S
y
b
2
2
*
0
=
, (2.31)
∑
=
+=
N
j
ji
b
b
b
X
N
nS
SS
ii
1
2
2
22
*
0
0
, (2.32)
∑
=
=
N
j
ji
y
b
X
S
S
i
1
2
2
2
)(
(где
i≠0), (2.33)
∑
=
=
N
j
jkji
y
kb
XX
S
S
i
1
2
2
2
)(
(где i≠k), (2.34)
∑
=
=
N
j
ji
y
b
X
S
S
ii
1
2*
2
2
)(
. (2.35)
Коэффициент
b
i
, считается значимым, если
nbi
tSb
i
,α
> . Аналогично проверя-
ется значимость остальных коэффициентов регрессии. Проверка адекватности
уравнения регрессии осуществляется с помощью критерия Фишера (2.18).
2.8. Метод ротатабельного планирования
Метод ротатабельного планирования эксперимента позволяет получать более
точное
математическое описание поверхности отклика по сравнению с ортого-
нальным ЦКП, что достигается благодаря увеличению числа опытов в центре
плана и специальному выбору величины «звездного» плеча α
. В табл. 2.7 приве-
дены основные характеристики матриц ротатабельного планирования.
20
Таблица 2.7
Характеристики ротатабельного ЦКП
Число
факторов
Число опытов
факторного
планирования
Число
опытов
в звездных
точках
Число
опытов
в центре
плана
Общее
число
опытов
α
2
3
4
5*
5**
4
8
16
32
16
4
6
8
10
10
5
6
7
10
6
13
20
31
52
32
1,414
1,680
2,000
2,378
2,000
* Полный факторный эксперимент.
** Эксперимент по методу дробных реплик.
При ротатабельном ЦКП для вычисления коэффициентов регрессии и соответ-
ствующих оценок дисперсий находят следующие константы:
[]
n)Β(nΒ
A
−+
=
22
1
, (2.36)
()( )
0
2 NNn
nN
Β
−+
=
, (2.37)
0
NN
N
C
−
=
, (2.38)
где
n – число факторов; N – общее число опытов ротатабельного ЦКП; N
0
– число
опытов в центре плана.
На основании результатов эксперимента вычисляют следующие суммы:
∑
=
=
N
j
j
yS
1
0
, (2.39)
∑
=
=
N
j
jji
i
yXS
1
(где i=1,2,…,n), (2.40)
∑
=
=
N
j
jjkjiik
yXXS
1
(где i ≠ k), (2.41)
∑
=
=
N
i
jjiii
yXS
1
2
(где i=1,…, n). (2.42)
Формулы для расчета коэффициентов регрессии имеют следующий вид:
()
⎥
⎦
⎤
⎢
⎣
⎡
−+=
∑
=
n
i
ii
SCnΒS
N
AΒ
b
1
00
2
2
, (2.43)
