Бондаренко В.В. Основы теории цепей. Часть 2
Подождите немного. Документ загружается.


121
=
э
+
э
+
Ф
(3)
Или в символической форме:
̇
=
э
̇
+
э
̇
+
Ф
̇
̇
(4)
Эквивалентная схема и векторная диаграмма изменятся.
в) Экспериментальное определение параметров эквивалентной
катушки.
(
)
,
(
)
,
(
)
,
к
,
1)
,
2)
к
,
с
3)
ф
,
п
4) g, b
5) δ
1)
=
э
cos
cos =
э
=arccos
э
u
i
V
A
W
Ф
̇
̇
̇
э
̇
п
̇
ф
̇
э
̇
э
̇
U
I
п
I
ф
r L
s
I
э
U
0

122
э
̇
=
э
̇
=
̇
−
э
̇
−
э
̇
2)
к
=
к
э
=
к
+
с
с
= −
к
3)
с
=
п
п
=
с
Из ВД найдём
ф
=
э
+
п
4)
п
=
=
п
ф
=
=
ф
5)
=
п
ф
=arctg
п
ф
123
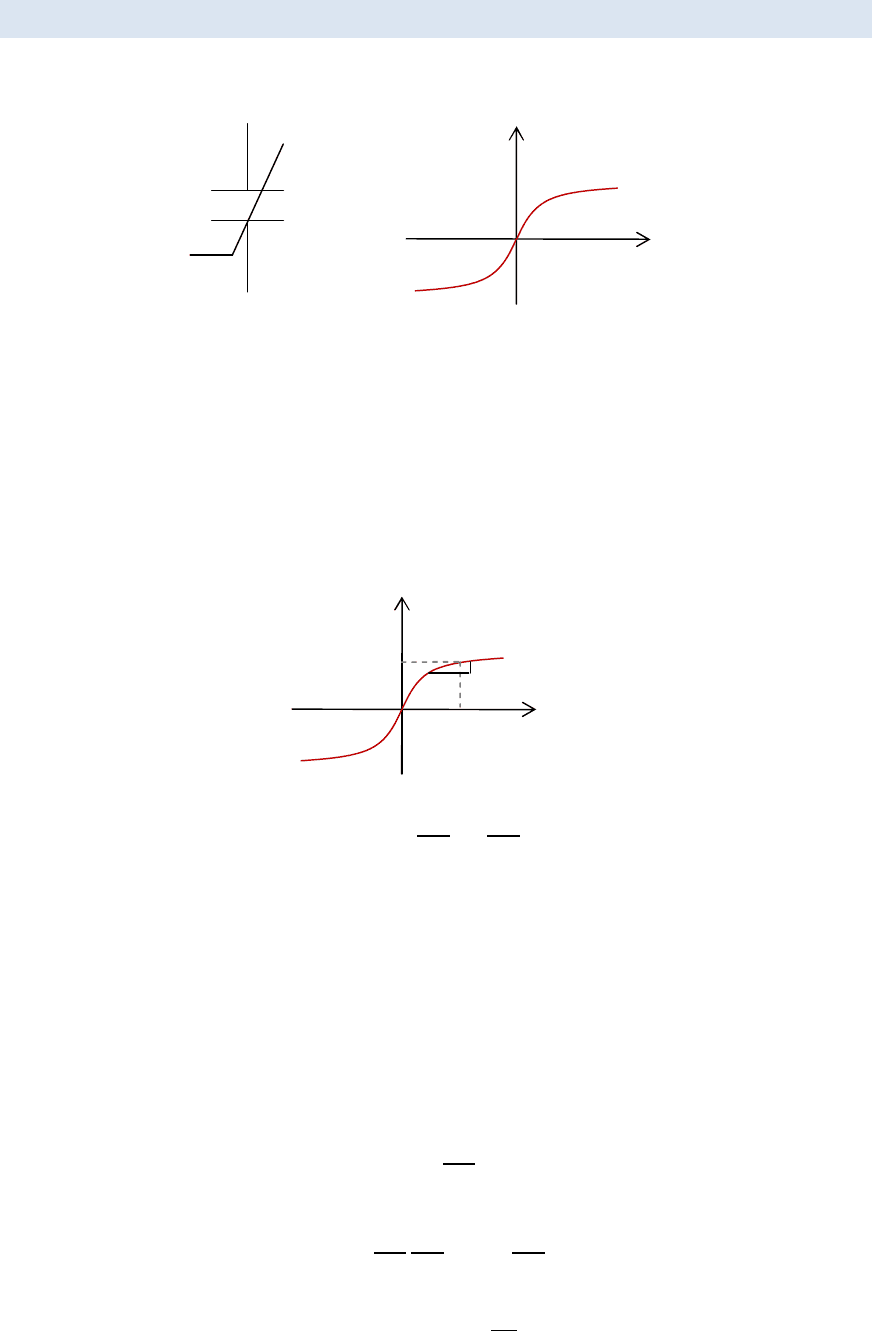
§6.7. БЕЗЫНЕРЦИОННАЯ НЕЛИНЕЙНАЯ ЁМКОСТЬ
Физический прототип — сегнетодиэлектрики.
=
(
)
Рассмотрим на этой КВХ рабочую точку А. В ней отношение
⁄
=
ст
— статическое.
д
=
Δ
Δ
≅
— динамическое, или дифференциальное.
ст
≠
д
Если
ст
=
д
, имеем частный случай: линейный элемент С.
Ток связан зависимостями
=
=
=
д
В линейных цепях мы писали =
. В нелинейных цепях это
утверждение несправедливо.
u
q
A
q
0
u
0
u
q
124
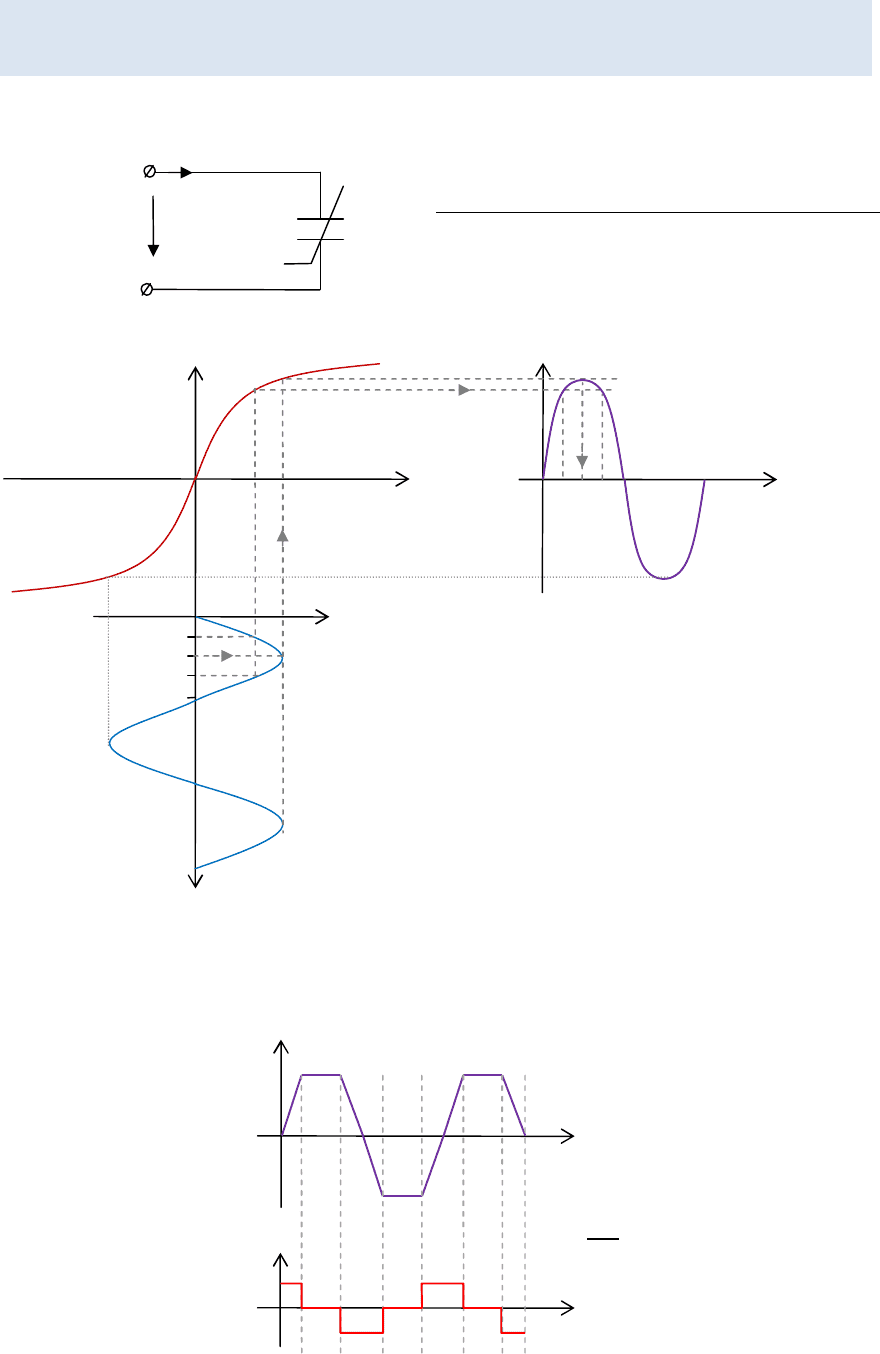
§6.8. ПОДКЛЮЧЕНИЕ БЕЗЫНЕРЦИОННОЙ НЕЛИНЕЙНОЙ
ЁМКОСТИ К ИСТОЧНИКУ СИНУСОИДАЛЬНОГО НАПРЯЖЕНИЯ
=
sin
КВХ
q, i
Стоит изменить форму синуса, как появляются гармоники.
t
q
t
i
=
u
q
t
u
t
0
1
2 3 4
0
1
2 3 4
q
T
T/2
T/2
T
u
i

125
Выводы:
1) Напряжение синусоидальное, однако заряд и ток — несину-
соидальные функции времени.
2) Раз они несинусоидальные, но периодические, значит, они
раскладываются в ряд Фурье и дают нам гармоники.
3) Любой нелинейный элемент приносит нам дополнительные
гармоники, то есть искажает спектральный состав, в отличие от
линейного элемента.
§6.9. ПАРАМЕТРИЧЕСКИЕ ЦЕПИ
Параметрическими цепями называются такие, параметры ко-
торых являются функциями времени.
= ( )
= ( )
= ( )
1) Например, угольный микрофон: R меняется от
звукового давления.
Если мы перемещаем индуктивность, то L будет
функцией времени.
Если мы раздвигаем пластины конденсатора, C будет функци-
ей времени.
2) Это особый класс цепей, которые обладают свойствами как
линейных, так и нелинейных цепей.
Как линейные цепи, они описываются линейными дифферен-
циальными уравнениями. Если ЭДС и напряжение увеличива-
ем в k раз, то и ток увеличится в k раз.
Как нелинейные цепи, они создают дополнительные гармони-
ки.
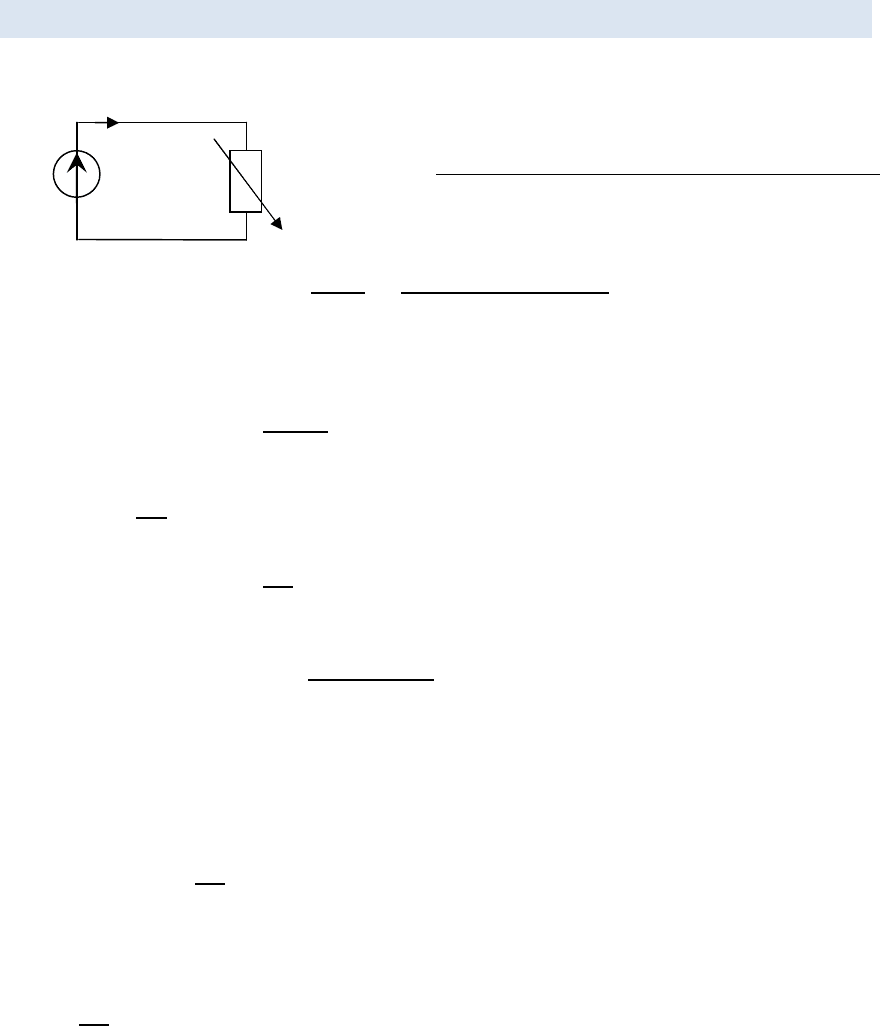
126
§6.10. ПОДКЛЮЧЕНИЕ ( ) К ПОСТОЯННОЙ ЭДС
=
=
(
1
−
sin
)
,
<
1
i
=
(
)
=
1
−
sin
(1)
1
1
−
=
1
+
+
+
+
⋯
(2)
=
(
1
+
sin
+
sin
+
sin
+
⋯
)
=
=
(
1
+
sin
+
sin
+
sin
+
⋯
)
(3)
sin =
1 −cos2
2
=0,5 −0,5cos2
sin
=
0
,
75
sin
−
0
,
25
sin
3
(4)
Подставим (4) в (3).
=
(
1+ sin +
(
0,5 −0,5cos2
)
+
+
(
0,75sin −0,25sin3
)
+⋯
)
=
(
1+
⋅0,5+⋯
)
+
(
+
⋅0,75+⋯
)
sin +
+
(
(
0,5
)
+ ⋯
)
cos2 +
(
(
−
)
0,25+..
)
sin3 +⋯
В спектре тока появились дополнительные высшие гармоники.
Амплитуды тока нелинейно зависят от b.
Но если мы в k раз изменим ЭДС, у нас в k раз изменятся ам-
плитуды тока.
R(t)
i
E

127
Глава 7. Электрические цепи с
распределёнными параметрами
1) До сих пор рассматривали сосредоточенные параметры.
2) До сих пор мы считали, что напряжение или ток могут зави-
сеть лишь от одной переменной: от времени.
Длина волны промышленной частоты:
= ⋅ =
1
=3⋅10
⋅
1
50 Гц
=6 000 км
Электрическими цепями с распределёнными парамет-
рами называются такие, параметры которых зависят не только
от времени, но и от расстояния (или координаты x).
=
(
,
)
=
(
,
)
Критерий: если Δ ≪ , то это цепь с сосредоточенными пара-
метрами, и координатой х можно пренебречь. А если Δ ~ , цепь
рассматриваем как цепь с распределёнными параметрами.
Примеры таких цепей: линии электропередачи, телефонные и
телеграфные линии: их длина соизмерима с длиной волны. Их
также называют «длинными линиями».
Но возьмём диапазон СВЧ (3 ГГц). Посчитаем длину волны.
=
=3⋅10
м
с
⋅
⋅
гц
=10 м — здесь длинные линии вовсе не
являются длинными.
x
x
Δ
x
128
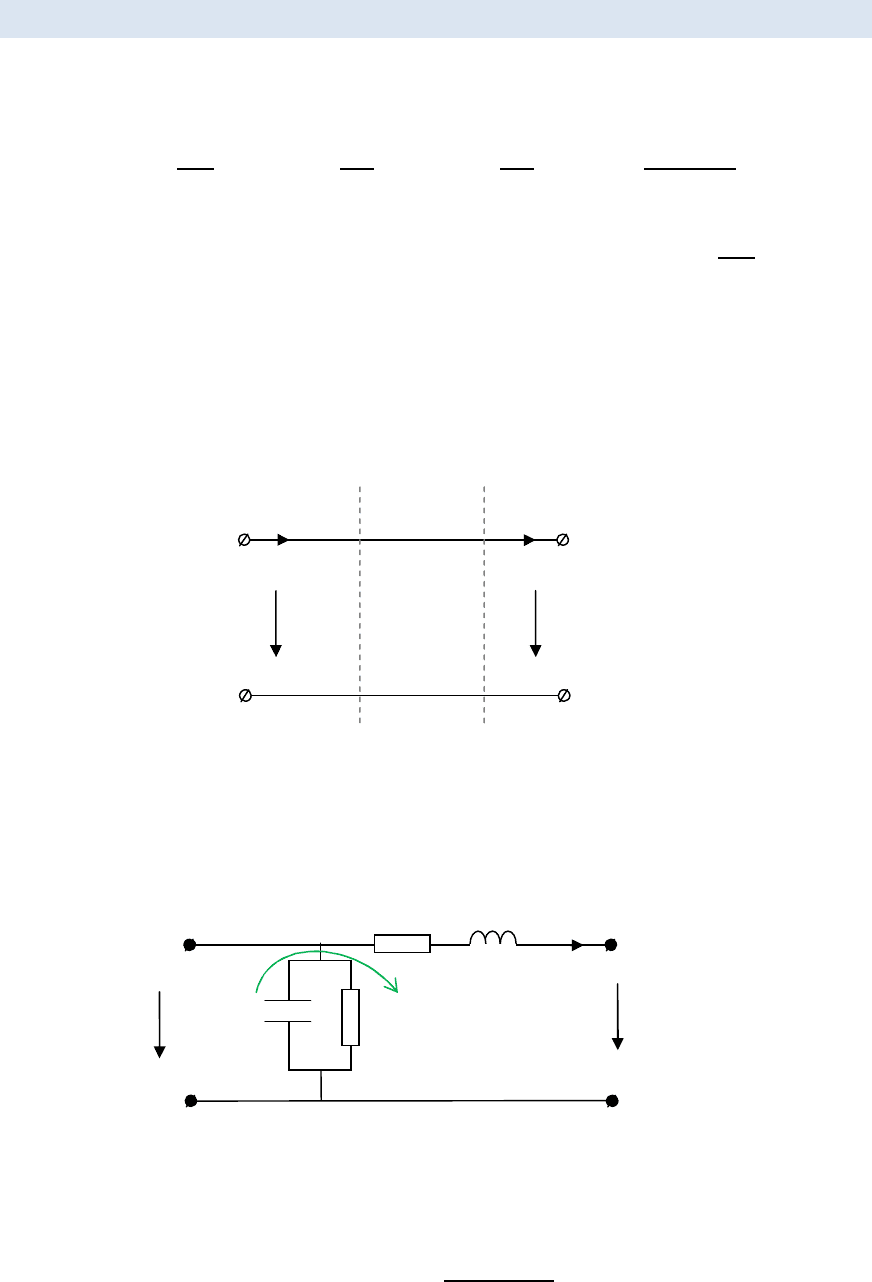
§7.1. УРАВНЕНИЕ ОДНОРОДНОЙ ДВУХПРОВОДНОЙ ЛИНИИ
Первичные параметры на единицу длины:
Ом
км
,
Гн
км
,
Ф
км
,
1
Ом ⋅км
Δ
[
Ом
]
,
Δ
[
Гн
]
,
Δ
[
Ф
]
,
Δ
1
Ом
Если первичные параметры не зависят от длины линии, то та-
кая линия называется однородной.
Рассмотрим некую длинную линию.
Между этими точками можем составить эквивалентную схему,
исходя из физического смысла: учтём потери.
Обойдём контур, составим уравнение по второму закону Кирх-
гофа.
− +
Δ
(
+ Δ
)
+
Δ
(
+Δ
)
+
(
+ Δ
)
=0
Пренебрежём величинами второго порядка малости.
u
u+
Δ
u
i+Δi
1’
2
2’
1
g
0
Δ
x
C
0
Δ
x
r
0
Δ
x
Δ
u
i
u+
Δ
u
i+Δi
1
1’
2
2’

129
− +
Δ +
Δ
+ + Δ =0
+
=
Δ
Δ
−
=
+
(1)
— первое телеграфное уравнение.
Составим уравнение по первому закону Кирхгофа для первого
узла.
−
(
+ Δ
)
−
Δ −
Δ
=0
−Δ −
Δ −
Δ
=0
−
Δ
Δ
=
+
Δ
−
=
+
(2)
— второе телеграфное уравнение.
§7.2. УСТАНОВИВШИЙСЯ ГАРМОНИЧЕСКИЙ ПРОЦЕСС
Процесс описывается символической формой.
⎩
⎨
⎧
−
̇
=
(
+
)
̇
−
̇
=
(
+
)
̇
(1)
(2)
Возьмём производную по dx от уравнения (1).
−
̇
=
(
+
)
̇
130
̇
=
(
+
)
−
̇
Подставим уравнение (2).
̇
=
(
+
)
(
+
)
̇
(3)
=
(
+
)
(
+
)
=
+
(4)
γ — коэффициент распространения волны.
— коэффициент затухания волны.
β — коэффициент фазы.
Вернёмся к уравнению (3).
̇
=
̇
̇
−
̇
=
0
(5)
— однородное дифференциальное уравнение второго порядка.
Характеристическое уравнение:
−
=0
=
=∓
Общее решение уравнения (5):
̇
=
̇
+
̇
(6)
— уравнение для напряжения в установившемся режиме.
̇
,
̇
— постоянные интегрирования, которые находятся из
граничных условий.
̇
=
,
̇
=
