Бобин Н.Е. Инженерная графика. Начертательная геометрия
Подождите немного. Документ загружается.

О
А
P=PPPi;
A
O
P=P
0
f
PPi;
A
O
PPi.
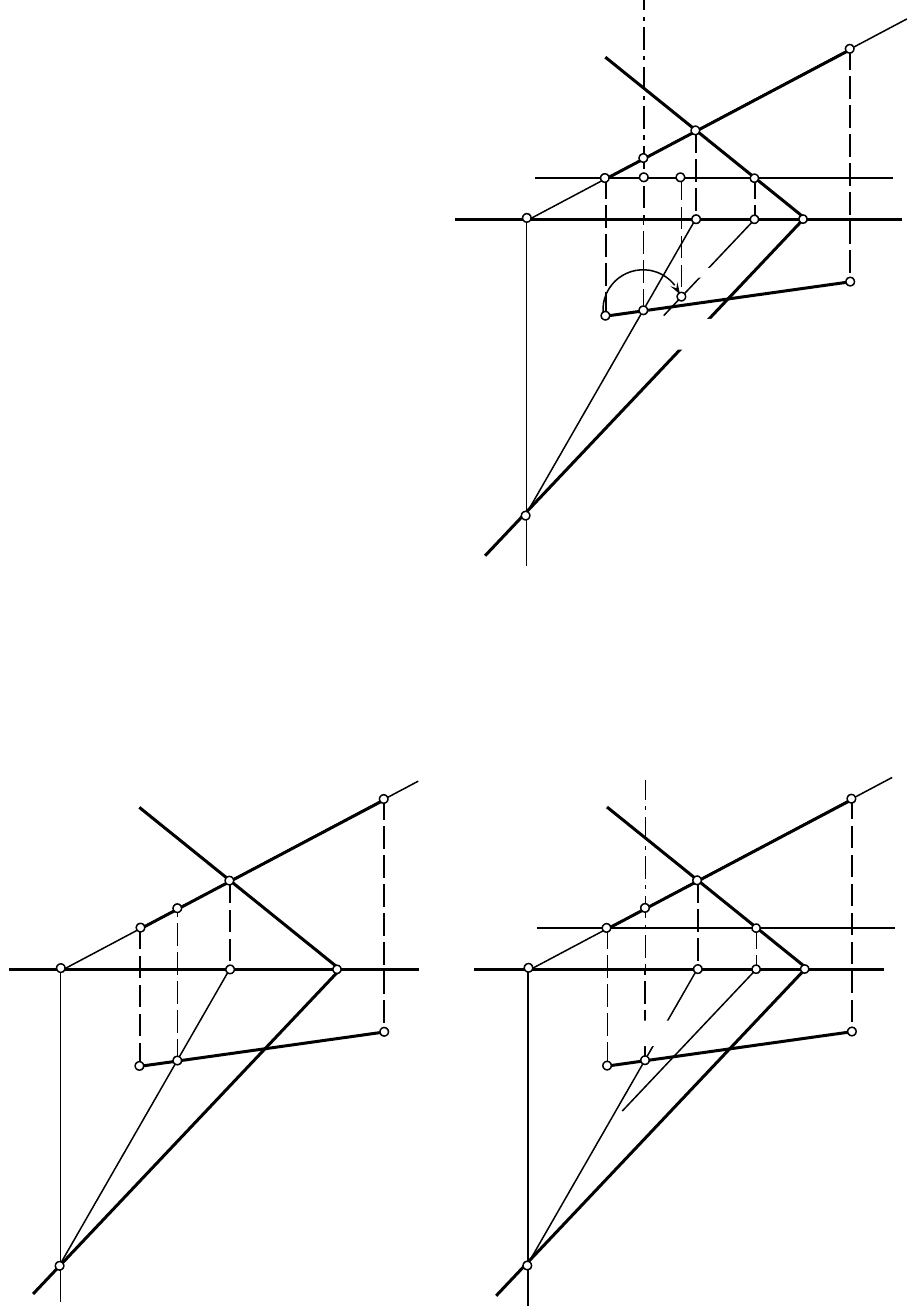
5.PОпределяем радиус вращения точки А: на горизонтальную плоскость проекций он
спроецировался в натуральную величину (
A
O
А).
51
Рис.12.4
2
N
γ0
f
α0
h
K
PPi
PP
1
N
2
N
1
N
β0
f
α0
f
А
А
X
x
В
А
В
X
β0
h
M
K
i
A
O
А
Рис.12.3
β0
f
γ0
f
1
N
2
N
2
N
1
N
K
PPi
А
X
x
α0
f
α0
h
В
А
В
X
β0
h
M
K
i
Рис.12.2
M
α0
f
β0
f
1
N
1
N
А
X
x
α0
h
В
А
В
X
β0
h
K
K
6.PТочка принадлежит одновременно двум плоскостям, если она принадлежит линии
пересечения этих плоскостей. Поэтому строим горизонтальную проекцию линии пересечения
плоскостей и : она пройдет через
2
N
параллельно следу
α0
h
.
7.PВращаем точку А вокруг оси i до положения
А, совмещенного с заданной
плоскостью . Горизонтальная проекция точки А (А) перемещается по дуге окружности
радиуса
A
O
А, фронтальная проекция точки А (А) – по следу
0
f
. Для построения
горизонтальной проекции
А проведем дугу окружности из центра
A
O
радиусом
A
O
А до
пересечения с горизонтальной проекцией линии пересечения плоскостей и .
Фронтальная проекция нового положения точки
А (
А) будет находиться на
0
f
.
Находясь на этой линии, точка А окажется в плоскости .
Вообще говоря, это вращение можно осуществить как по часовой стрелке, так и против,
поэтому задача имеет два решения. Поскольку в условии задачи направление вращения не
оговаривается, мы вправе выбрать направление самостоятельно. В рассматриваемом примере
вращение точки А проведено по часовой стрелке;
А – горизонтальная проекция в
совмещенном с плоскостью положении, а
А – ее фронтальная проекция.
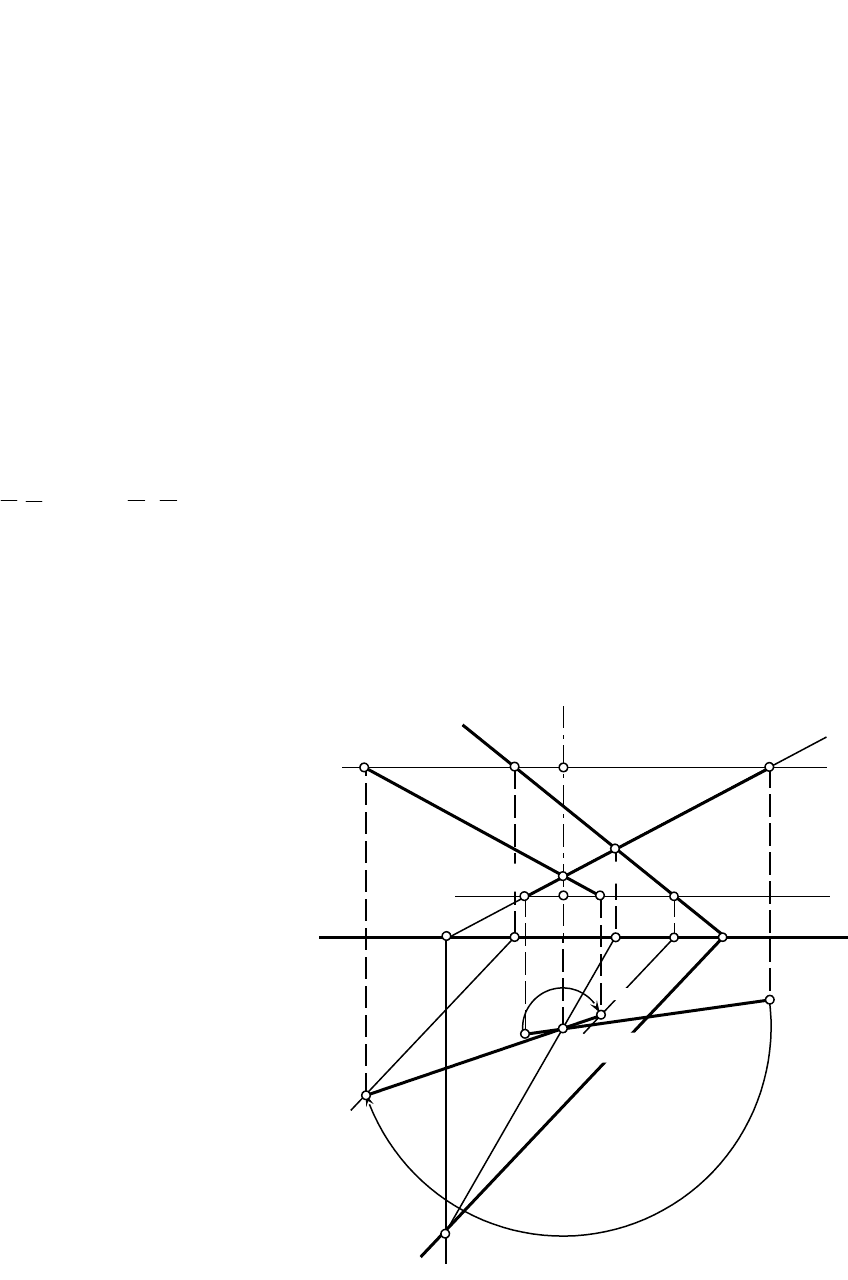
8.PАналогично совмещаем с плоскостью точку В (рис.12.5), проведя плоскость ее
вращения .
9.PСоединяем одноименные проекции точек А (
А,
А) и В (
В,
В) и проверяем
правильность построений. Поскольку точка K с одной стороны лежит на прямой АВ, а с
другой – на оси вращения i, при вращении прямой АВ ее положение не изменяется:
KPP
BA
; KPP
.BA
52
1
N
Рис.12.5
2
N
α0
h
K
i
1
N
K
2
N
3
N
β0
h
γ0
f
β0
f
ε0
f
B
O
3
N
X
x
α0
f
В
А
В
X
M
i
A
O
В
В
А
А
А
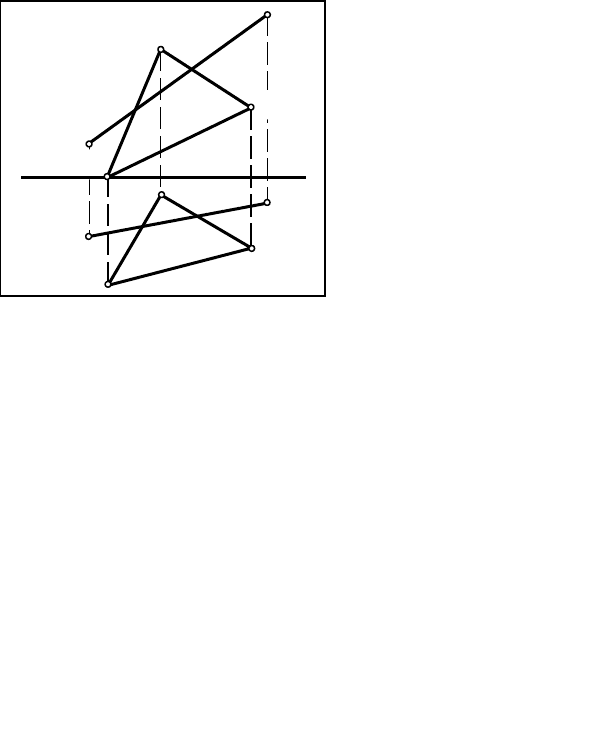
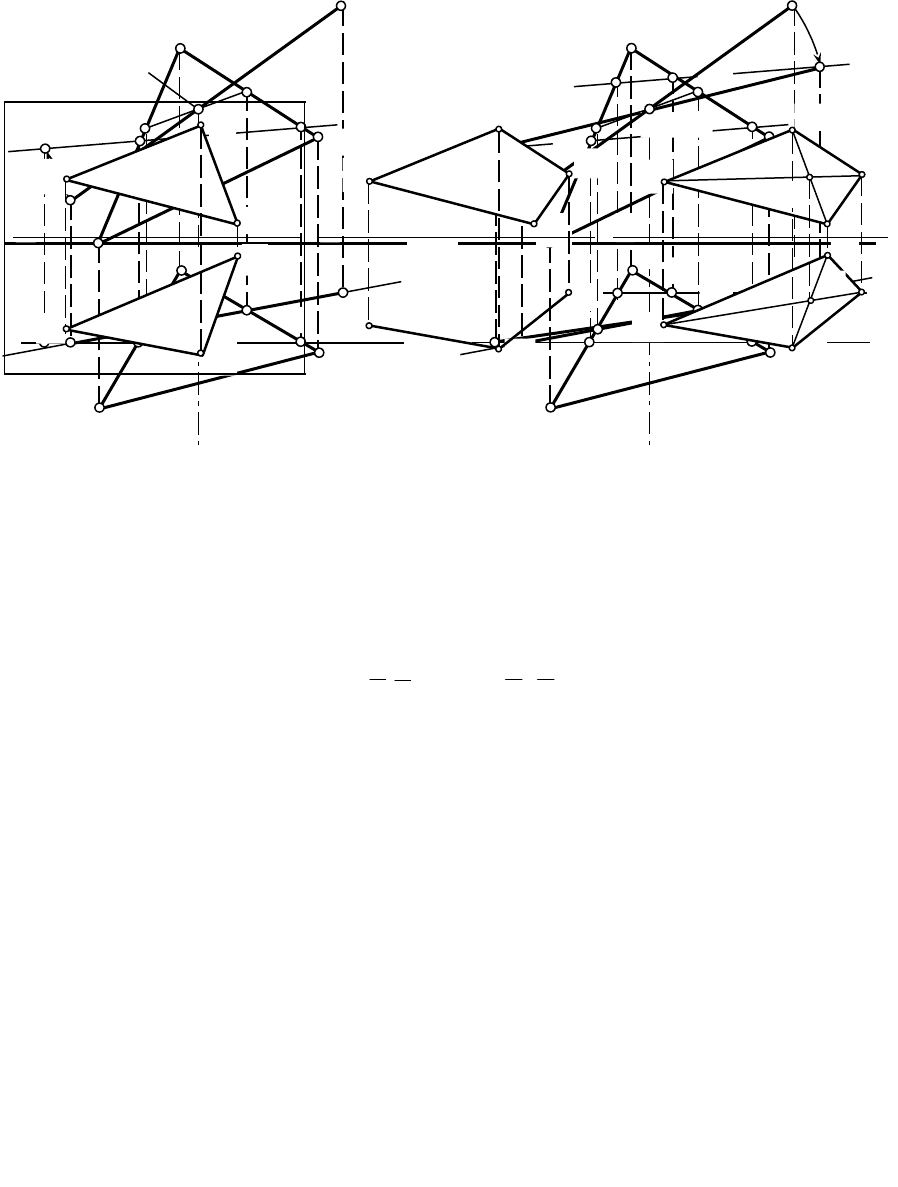
12.2. Плоскость задана плоской фигурой (рис.12.6)
1.PСтроим точку пересечения K (K и K) заданной прямой АВ с плоскостью
треугольника EDF (рис.12.7) – см. задачу 7.
2.5Через точку K проводим ось вращения i (рис.12.8),
перпендикулярную плоскости проекций
2
:
i""x; i""K.
3.5Совмещаем с плоскостью треугольника EDF любую точку прямой
АВ, например точку А. Проводим плоскость вращения точки А – плоскость :
""i и А""""А""
γ0
h
и
γ0
h
""i.
4.PОпределяем центр вращения О
А
точки А (О
А
P=PPPi, рис.12.9):
A
O
=
γ0
h
i;
A
O
i.
53
A
D
x
B
A
B
E
F
D
E
F
Рис.12.6
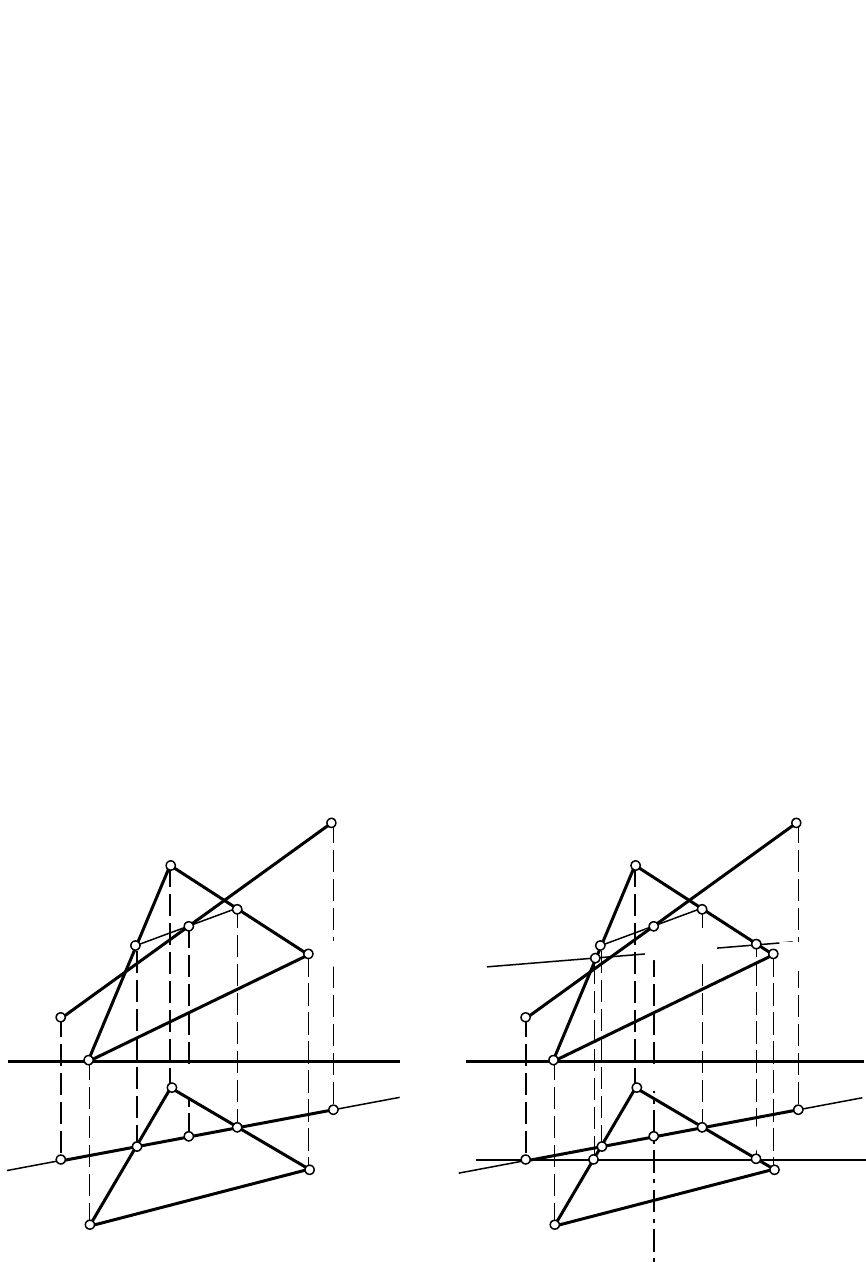
5.PОпределяем радиус вращения точки А: на фронтальную плоскость проекций он
спроецировался в натуральную величину (
A
O
А).
6.PТочка принадлежит одновременно двум плоскостям, если она принадлежит линии
пересечения этих плоскостей. Поэтому строим линию пересечения 34 плоскости и плоскости
треугольника EDF.
7.PВращением вокруг оси i совмещаем с плоскостью треугольника EDF точку А. Строим
проекции точки А в совмещенном с плоскостью треугольника EDF положении. Фронтальная
проекция точки А (А) перемещается по дуге окружности радиуса
A
O
А, и в пересечении с
34 точка А совмещается с плоскостью треугольника EDF:
АPP34.
Горизонтальная проекция точки А (А) перемещается по следу
0
h
:
АPP
0
h
.
54
Рис.12.7
E
β0
h
1
A
E
2
2
K
D
x
B
A
B
F
D
F
K
1
Рис.12.8
γ0
h
3
B
4
E
β0
h
A
4
E
2
2
K
i
1
D
x
B
A
F
D
F
K
1
i
3
7.PАналогично строим проекции
В и
В точки В, проведя плоскость вращения
(рис.12.10). При этом имеем в виду, что фронтальные проекции фронталей плоскости
треугольника EDF взаимно параллельны, т.е.
56PP34.
8.PСоединяем одноименные проекции точек А (
А,
А) и В (
В,
В) в совмещенном с
плоскостью треугольника EDF положении и проверяем правильность построений:
KPP
BA
; KPP
.BA
Задача 13
Методом вращения вокруг оси, параллельной плоскости проекций, определить
истинную величину плоской фигуры.
Индивидуальное задание представлено на рис.13.1.
55
Рис.12.10
5
γ0
h
ε0
h
β0
h
4
E
6
2
2
3
5
6
A
K
PPi
1
D
x
B
A
B
E
F
D
F
K
1
A
i
B
4
3
A
B
Рис.12.9
E
K
PPi
PP
3
A
O
γ0
h
β0
h
4
E
2
2
A
1
D
x
B
A
B
F
D
F
K
1
A
i
4
3
A
B
B
C
A
D
C
A
x
Рис.13.2
B
C
A
D
B
C
A
D
K
x
K
Рис.13.3
B
C
A
x
C
A
B
Рис.13.1
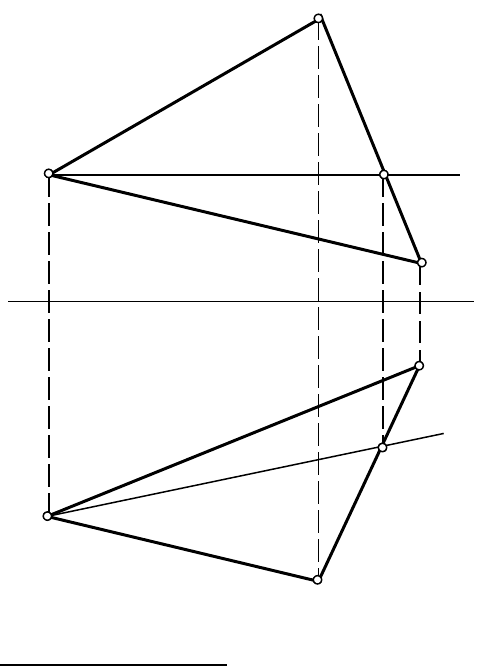
Для решения этой задачи необходимо вспомнить материал раздела 4.4. «Проецирование
плоских фигур. Пересечение плоских фигур» учебного пособия [3]. Если плоская фигура задана
многоугольником с количеством сторон, большим чем три, то первоначально необходимо
построить недостающие проекции вершин так, чтобы все точки этой фигуры находились в одной
плоскости. Например, четырехугольник может быть задан двумя проекциями трех его вершин и
лишь одной проекцией четвертой вершины (рис.13.2). Недостающая проекция вершины лежит на
пересечении линии проекционной связи, проведенной из имеющейся проекции вершины
многоугольника, и проекции диагонали, проходящей, в свою очередь, через точку пересечения
диагоналей (рис.13.3).
1.PДля нахождения истинной величины заданного треугольника ABC повернем его
вокруг горизонтали в положение, параллельное плоскости проекций
1
, тогда горизонтальная
проекция фигуры будет представлять собой ее истинную величину
.
2.PВ плоскости ABC, например, через точку C проводим горизонталь C1 (рис.13.4):
C1PPx; 1PPAB.
Эту горизонталь принимаем за ось вращения. Точки, в том числе и вершина С треугольника,
оказавшиеся на оси вращения, при вращении своего положения не меняют:
CPPС .
3.PПроводим плоскость вращения γ
1
точки В (рис.13.5): горизонтальный след плоскости
вращения
1
0
h
проходит через B и перпендикулярен C1 (эта плоскость является
горизонтально-проецирующей; фронтальный след плоскости вращения для решения задачи не
используется и на чертеже он не указан).
4.PОпределяем проекции центра вращения точки В (О
В
) в пересечении плоскости
вращения и оси вращения:
Истинную величину плоской фигуры можно найти и путем вращения вокруг фронтали.
56
1
B
Рис.13.4
B
1
A
A
x
C
C
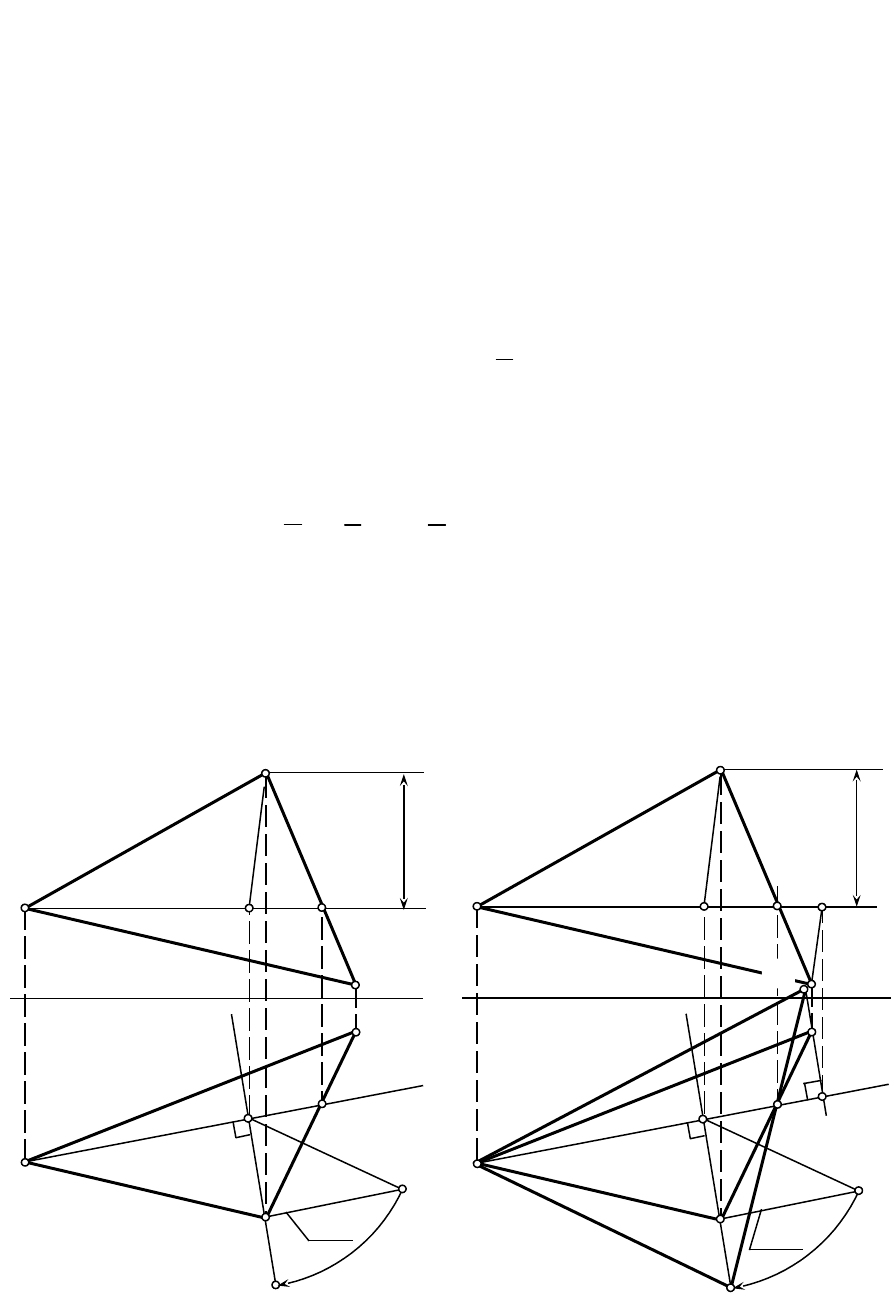
B
O
P=P
1
0γ
h
PPC1;
B
O
PPС1.
5.PРадиус вращения точки В на горизонтальную (
B
O
В) и фронтальную (
B
O
В)
плоскости проекций спроецирован с искажением. Определяем истинную величину радиуса
вращения точки В (R
B
) методом прямоугольного треугольника, одним катетом которого
является горизонтальная проекция радиуса вращения
B
O
В, а другим катетом расстояние,
равное алгебраической разности координат z
В
.
6.PОпределяем горизонтальную проекцию нового положения вершины В (
В). На
пересечении дуги окружности радиусом R
B
, проведенной из
B
O
, и следа плоскости
вращения
1
0
h
отмечаем
В:
ВPP
;
1
0
h
ВO
B
P=PR
В
.
7.PДля построения нового положения точки А не обязательно определять истинную
величину ее радиуса вращения. Точка 1 (1PPАВ) при вращении АВС остается неподвижной,
поэтому новое положение
А можно найти в пересечении прямой
В1 с горизонтальным
следом плоскости вращения точки А –
2
0γ
h
(рис.13.6).
8.PСоединив точки
А
,
В
и
С
, получаем истинную величину заданного
треугольника.
Задача 14
По истинной величине плоской фигуры, принадлежащей плоскости и вписанной в
окружность радиуса R с заданным центром О, построить ее проекции. Задачу решить
способом совмещения.
57
Рис.13.5
B
O
B
O
1
0γ
h
B
1
x
A
1
C
B
C
P
B
0
A
B
R
B
z
B
z
B
C
P
1
A
O
Рис.13.6
2
0γ
h
B
1
x
A
B
O
C
B
B
0
A
B
O
B
R
B
z
B
z
B
1
0γ
h
A
O
A
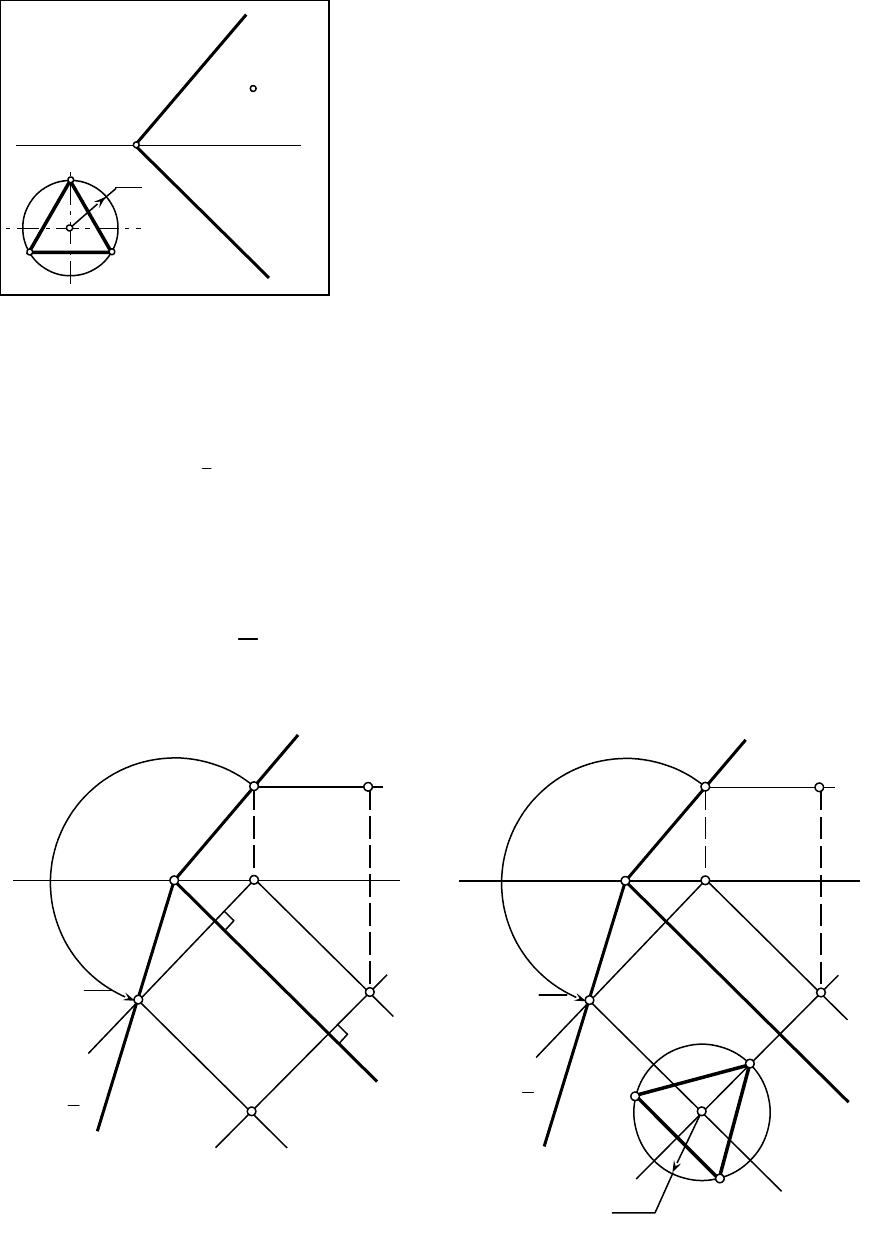
14.1.Плоскость общего положения (рис.14.1)
1.PЧерез точку О проводим горизонталь плоскости и определяем положение
горизонтальной проекции точки О (О) (рис.14.2) – см. задачу 4.
2.PСовместим плоскость с горизонтальной плоскостью проекций путем ее вращения
вокруг следа
α0
h
. След
α0
h
, как ось вращения, своего положения не меняет; точка схода
следов X
также не изменяет своего положения. Поэтому для построения нового положения
фронтального следа
α0
f
плоскости , совмещенного с плоскостью
1
, достаточно найти одну
точку этого следа в совмещенном положении.
Совместим с плоскостью
1
точку N
1
(N
1
PP
α0
f
). Проведем плоскость вращения
1
точки N
1
:
1
N
PP
1
0γ
h
;
1
0γ
h
PP
α0
h
.
Новая проекция
1
N
находится на пересечении дуги окружности радиуса X
1
N
со
следом плоскости вращения
1
0γ
h
.
58
Рис.14.2
α0
f
1
N
1
N
1
N
α0
f
X
x
α0
h
1
0γ
h
О
О
О
2
0γ
h
α0
f
α0
f
2
0γ
h
1
N
1
0γ
h
1
N
1
N
X
x
α0
h
Рис.14.3
С
А
О
О
В
О
R
R
О
α0
f
X
x
α0
h
О
RP=P12
Рис.14.1

3.PЧерез
1
N
и X
проведем совмещенное с горизонтальной плоскостью проекций
положение фронтального следа плоскости
α0
f
.
4.PСовместим с плоскостью
1
горизонталь N
1
O, которая в совмещенном положении
будет проходить через
1
N
параллельно горизонтальному следу
α0
h
.
59
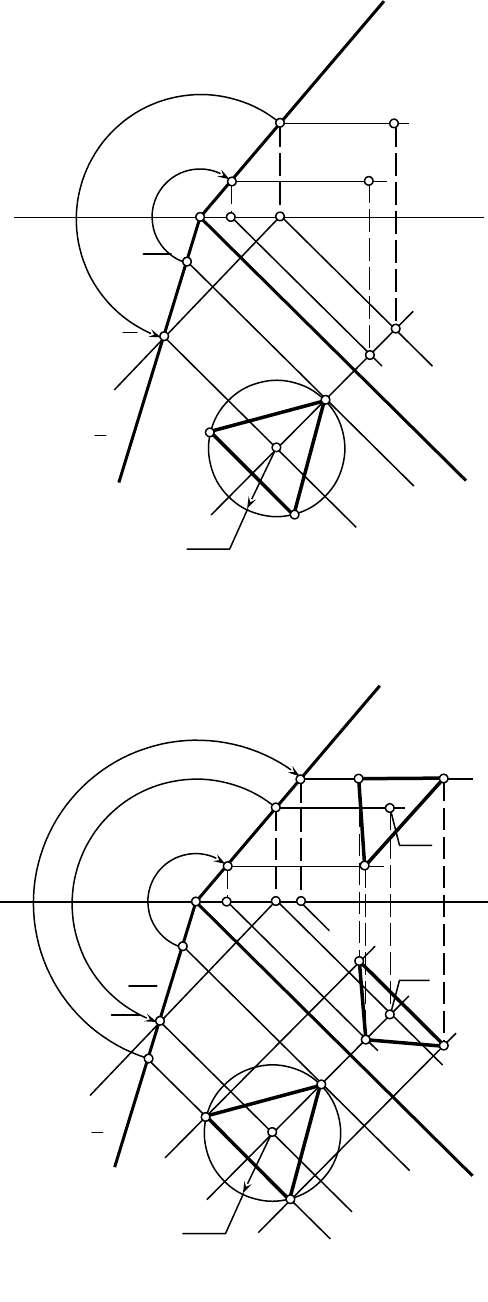
5.PНайдем совмещенное с
плоскостью
1
положение точки О.
Проведем плоскость вращения точки О:
60
Рис.14.4
1
0γ
h
α0
f
2
0γ
h
2
N
1
N
1
N
1
N
2
N
В
2
N
α0
f
X
x
α0
h
С
А
О
О
О
R
B
B
Рис.14.5
3
N
1
0γ
h
1
N
2
N
1
N
3
N
4
0γ
h
α0
f
2
0γ
h
3
0γ
h
α0
h
1
N
2
N
В
В
В
α0
f
X
3
N
x
А
С
А
А
С
С
О
О
О
R
