Blum W., Riegler W., Rolandi L. Particle Detection with Drift Chambers

Подождите немного. Документ загружается.

Chapter 5

Creation of the Signal

The moving charges in a chamber give rise to electrical signals on the electrodes

that can be read out by ampliﬁers. The electrons created in the avalanche close to the

wire move to the wire surface within a time typically much less than a nanosecond,

resulting in a short signal pulse. The ions created in the avalanche move away from

the wire with a velocity about a factor 1000 smaller, which results in a signal with

a long tail of typically several hundred microseconds duration. The movement of

these charges induces a signal not only on the wire but also on the other electrodes

in the chamber, so for the purpose of coordinate measurements the cathode can

be subdivided into several parts. In this chapter we derive very general theorems

that allow the calculation of signals in wire chambers and present some practical

examples.

5.1 The Principle of Signal Induction by Moving Charges

In order to understand how moving charges give rise to signals on electrodes we

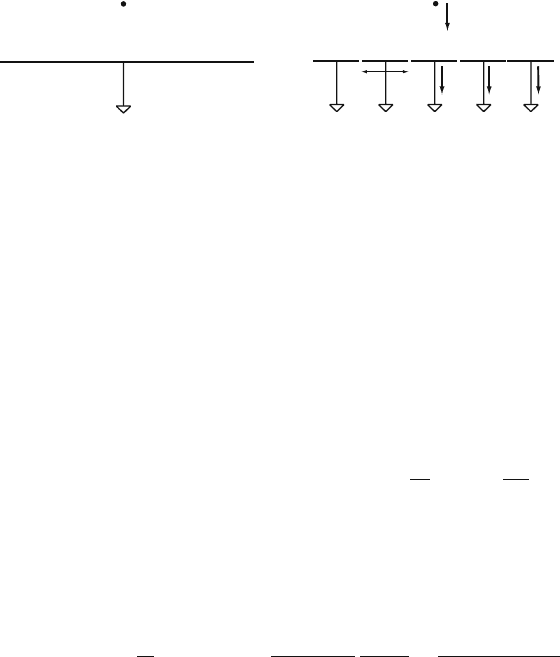
ﬁrst consider the simple example shown in Fig. 5.1a [JAC 75]. A point charge

q in the presence of a grounded metal plate induces a charge on the metal sur-

face. This surface charge can be calculated by solving the Poisson equation for

the potential

with a point charge q at z = z

and the boundary condition that

= 0atz = 0. Gauss’ law tells us that the resulting electric ﬁeld E = −∇

on the metal surface is related to the surface charge density

(x,y)=

E(x, y,z = 0). The solution for this particular geometry can be found by assum-

ing a mirror charge −q at z = −z

. The electric ﬁeld on the metal surface is thus

given by

(x,y)=−

πε

+ y

+ z

)

= E

= 0, (5.1)

and the surface charge density is

(x,y)=

(x,y). The total charge induced on

the metal plate is therefore

W. Blum et al., Particle Detection with Drift Chambers, 157

doi: 10.1007/978-3-540-76684-1

 Springer-Verlag Berlin Heidelberg 2008

158 5 Creation of the Signal

σ (x,y)

0 000

(t) Q

(t)

z = z

z = 0

Fig. 5.1 (a) A point charge q induces a charge density

(x,y) on the surface of a grounded metal

plate. (b) Segmenting the metal plate results in induced charges Q

on the strips. In case q is

moving, the induced charges on the strips are changing and currents are ﬂowing between the

strips and ground

Q =



∞

−∞



∞

−∞

(x,y)dxdy = −q, (5.2)

and it is independent of the distance of the charge q from the metal plate. Let us now

imagine the metal plate to be segmented into strips of width w, each of the strips

being grounded (Fig. 5.1b). In order to ﬁnd the charge induced, e.g., on the central

strip, we have to integrate the surface charge density from Eq. (5.1) over the area of

the strip:



∞

−∞



w/2

−w/2

(x,y)dxdy = −

arctan





. (5.3)

This induced charge now depends on the distance z

of the point charge q from

the metal surface. If the charge is moving towards the metal strip with a velocity v

according to z

(t)=z

−vt, we ﬁnd a time-dependent-induced charge Q

(t)] and

thus an induced current of

ind

(t)=−

(t)] = −

∂

(t)]

∂

(t)

4qw

[4z

(t)

+ w

]

v. (5.4)

We see that the movement of a charge induces a current which ﬂows between the

electrode and ground. This is the principle of signal induction by moving charges.

For more realistic geometries, this method of calculating the signals is the same but

can become quite complex. In the following we derive theorems that allow a simpler

and more intuitive way of calculating signals induced on grounded electrodes. After

that we investigate the signals for the scenario where the electrodes are not grounded

but are connected to ampliﬁers or interconnected by a general reactive network.

5.2 Capacitance Matrix, Reciprocity Theorem

The capacitance matrix and the reciprocity theorem are the bases for the discussion

of signals induced on metal electrodes. The expression ‘metal’ electrode refers to the

condition that the charges on the electrode can move and that the electrode surface

5.2 Capacitance Matrix, Reciprocity Theorem 159

is therefore an equipotential one. Setting a set of N metal electrodes to voltages

deﬁnes the potential

(x) and the resulting electric ﬁeld E(x)=−∇

(x) in

the chamber volume. The potential is uniquely deﬁned by the conditions that

(x)

satisﬁes the Laplace equation and that

(x)=V

on the electrode surfaces.

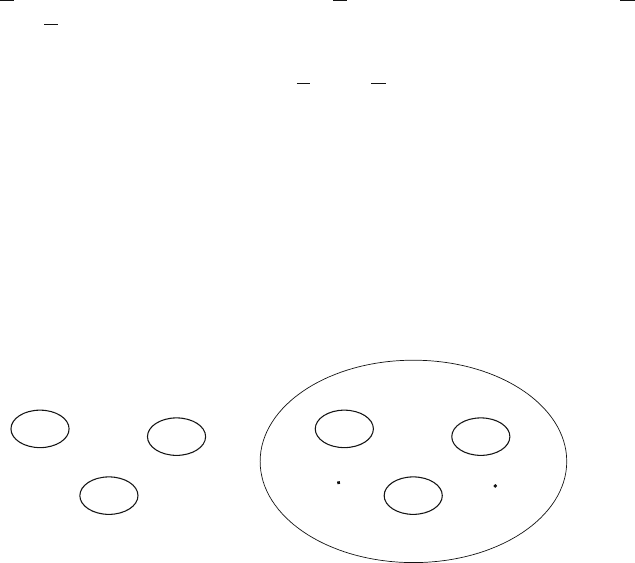
Figure 5.2a shows a set of three metal electrodes. The voltages V

and charges

on the electrodes are related by the capacitance matrix of the electrode system

[JAC 75]:

∑

m=1

. (5.5)

The capacitance matrix is deﬁned by the electrode geometry, and for the capacitance

matrix elements c

, the following relations hold:

= c

, c

≤ 0forn = m, c

≥ 0,

∑

m=1

≥ 0. (5.6)

These relations are a direct consequence of Green’s second theorem and the fact

that the potential has to satisfy the Laplace equation. A set of different voltages

is related to a set of different charges Q

by the same capacitance matrix Q

∑

, so by inverting this relation and multiplying it by Eq. (5.5) we ﬁnd

∑

n=1

∑

n=1

. (5.7)

This relation is called is called the reciprocity theorem and we use it frequently in

the following discussions. Another important relation concerns the sum of all the

charges of an electrode system. Figure 5.2b shows an electrode surrounding three

electrodes. We apply Gauss’ law to the volume between the electrodes, which tells

us that the sum of all charges within this volume is equal to

times the integral of

E(x) over the surface surrounding it. Because



E(x)dA over a metal electrode

is equal to the charge on this electrode, we ﬁnd that the sum of all charges on the

Fig. 5.2 (a) The voltages and charges in a system of electrodes are related by the capacitance

matrix c

. (b) A set of metal electrodes where one electrode encloses the others. The sum of all

charges Q

on the electrodes is equal to the sum of all charges q

in the volume between the

electrodes

160 5 Creation of the Signal

metal electrodes is equal to the sum of all charges in the volume between the elec-

trodes! In the case where there are no charges in the volume between the electrodes,

the sum of the charges Q

on the electrodes must be zero for any set of voltages V

applied to them. Thus for the capacitance matrix we ﬁnd the relation

∑

= 0 →

∑

= 0 →

∑

= 0, (5.8)

which means that for a set of electrodes that is enclosed by one of them, the sum of

all columns (rows) of the capacitance matrix is equal to zero.

To conclude this section we note that the capacitance matrix elements c

are

different from the more familiar capacitances C

that we know from electric circuit

diagrams. The C

are related to the voltage difference between circuit nodes, and

we show later that the c

and C

are related by

∑

m=1

, C

= −c

if n = m. (5.9)

5.3 Signals Induced on Grounded Electrodes, Ramo’s Theorem

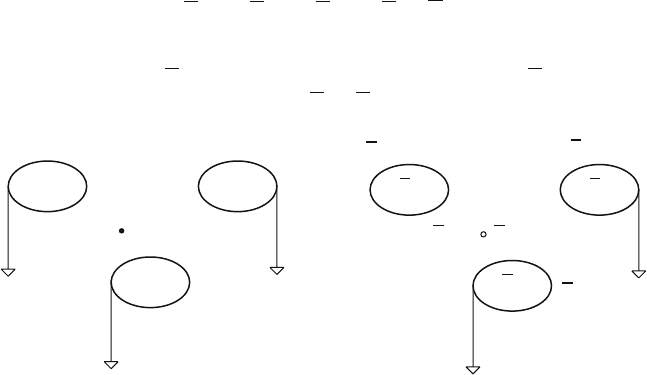
We consider a set of three grounded electrodes in the presence of a point charge

= q at position x as shown in Fig. 5.3a. We assume the point charge Q

to be

sitting on an (inﬁnitely small) metal electrode, so we have a system of four metal

electrodes. For this setup we haveV

= 0 and we want to know the charges

induced by the presence of charge Q

= q. Equation (5.7) reads

+ Q

= Q

. (5.10)

Choosing another electrostatic state (Fig. 5.3b), where we remove the charge q from

the small electrode (

= 0), we set electrode 1 to voltage V

= V

) while

keeping the other electrodes grounded (

= V

= 0), the above relation becomes

(x)

(a)

(b)

Fig. 5.3 (a) The point charge q induces charges Q

on the grounded electrodes. (b) Another set of

voltages and charges which deﬁnes the ‘weighting potential’ of the ﬁrst electrode

5.4 Total Induced Charge and Sum of Induced Signals 161

Fig. 5.4 In the case where

the charge q is moving there

are currents ﬂowing between

the electrodes and ground.

The deﬁnition of I = −dQ/dt

indicates that the positive

current points away from the

electrode

(t)

x(t)

(t) I

(t)

+ Q

= 0 → Q

= −q

. (5.11)

is the potential of the uncharged small electrode for the second electrostatic state,

and since an inﬁnitely small uncharged electrode is equal to having no electrode,

is the potential at point x when the point charge q is removed, electrode 1 is put to

potential V

, and electrodes 2 and 3 are grounded. We call V

(x) the weighting

potential of electrode 1, and the induced charge Q

is given by

= −

(x). (5.12)

In the case where the point charge q is moving along a trajectory x(t),asshown

in Fig. 5.4, we ﬁnd a time-dependent-induced charge on electrode n and therefore a

current of

ind

(t)=−

(t)

∇

[x(t)]

dx(t)

= −

[x(t)] v(t). (5.13)

We call E

(x)=−∇

(x) the weighting ﬁeld of electrode n, which is Ramo’s

theorem [RAM 39]:

The current induced on a grounded electrode by a point charge q moving along

a trajectory x(t) is I

ind

(t)=−q/V

[x(t)] v(t), where E

(x) is the electric ﬁeld

in the case where the charge q is removed, electrode n is set to voltage V

, and all

other electrodes are grounded.

It must be noted that the sign of the induced current is given not only by the sign

of the charge but also by the orientation of the particle velocity vector with respect

to the direction of the weighting ﬁeld. The trajectory x(t) is determined by the ‘real’

electric and magnetic ﬁelds in the detector together with the drift properties of the

electrons and ions in the detector gas.

5.4 Total Induced Charge and Sum of Induced Signals

If the charge q is moving along a trajectory x(t) from position x

= x(t

) to position

= x(t

), the total amount of charge Q

ind

that ﬂows between electrode n and

ground is given by

162 5 Creation of the Signal

ind



ind

(t)dt = −



[x(t)] ˙x(t)dt =

[

) −

)]. (5.14)

We ﬁnd that this induced charge depends only on the end points of the trajectory and

is independent of the speciﬁc path. If a pair of charges q, −q is produced at point x

at t = t

and q arrives at position x

while −q arrives at position x

after a time t

the charge induced on electrode n is given by

ind



ind

(t)dt =

[

) −

)]. (5.15)

If the charge q moves to the surface of electrode n while the charge −q moves to

the surface of some other electrode, the total induced charge on electrode n is equal

to q, since

= V

on electrode n and

= 0 on the other electrodes. When both

charges move to other electrodes, the total induced charge on electrode n is zero.

We can therefore conclude:

After all the charges have arrived at the different electrodes, the total charge

induced on electrode n is equal to the charge that has arrived at electrode n.

From this we also conclude that the current signals on electrodes that do not

receive any charge are strictly bipolar.

If we want to know the sum of the signals induced on several electrodes we can

either calculate the weighting ﬁelds and induced currents for the individual elec-

trodes and add the currents or we can calculate the weighting ﬁeld for the entire set

of electrodes by setting all of them to voltage V

and grounding the remaining ones.

Let us assume the set of electrodes shown in Fig. 5.5, where one electrode encloses

the others. The weighting potential

tot

for the sum of all induced currents is deﬁned

by setting all electrodes to potential V

. This, however, results in

tot

(x)=V

in the

entire volume and consequently a weighting ﬁeld of E

tot

(x)=0. We can therefore

conclude:

The sum of all induced currents on grounded electrodes is zero at any time, pro-

vided there is one electrode enclosing all the others.

(t)

(t) I

(t)

Fig. 5.5 A set of grounded electrodes enclosed by one electrode. The sum of all induced currents

is zero at any given time

5.5 Induced Signals in a Drift Tube 163

5.5 Induced Signals in a Drift Tube

As an example we calculate the induced signal in a drift tube with (cathode) radius b

and wire radius a (Fig. 5.6). The tube is set to potential −U and the wire is grounded.

This results in an electric ﬁeld of E(r)=U/(r ln(b/a)), as calculated in Sect. 3.1.1.

We assume a single primary electron-ion pair in the gas volume. The electron moves

to the wire and the ion moves to the tube wall. Close to the wire the electron starts an

avalanche creating N

tot

electrons and ions. The N

tot

electrons of charge −e

move to

the wire surface within a time much less than a nanosecond. The N

tot

ions of charge

move away from the wire, but much more slowly, arriving at the tube wall after

a time typically several hundreds of microseconds. As a ﬁrst step we simply assume

that the N

tot

electrons are created at the wire surface and so do not move, while the

tot

ions move from the wire surface to the tube wall. The velocity of the ions is

given by the mobility

as v =

E, so with the condition that r(t = 0)=a we ﬁnd

the ion trajectory to be

dr(t)

r(t)ln(b/a)

→ r(t)=a



ln(b/a)

(5.16)

The characteristic time t

is typically one or a few nanoseconds. It takes very much

longer for the ions to arrive at the tube wall r = b; this maximum travel time is

max

= t

[(b/a)

−1], typically four to six orders of magnitude larger than t

,inthe

hundred microsecond range.

The weighting potential

and weighting ﬁeld E

of the wire are deﬁned by

setting the wire to potential V

and grounding the tube, which results in

(r)=−

ln(r/b)

ln(b/a)

(r)=

rln(b/a)

(5.17)

According to Eq. (5.13), the current induced on the wire by the movement of the

tot

ions is given by

ind

(t)=−

tot

[r(t)] ˙r(t)=−

tot

2ln(b/a)

t + t

. (5.18)

The wire signal is negative and has a hyperbolic form with a characteristic time

constant t

, which in practical cases will be a few nanoseconds. The induced charge

at time t is given by

Fig. 5.6 Ions moving from

thewiresurfacetothetube

wall induce a current signal

on the grounded wire

–U

I(t)

164 5 Creation of the Signal

ind

(t)=



ind



)dt



= −

tot

2ln(b/a)





. (5.19)

Once the ions have arrived at the tube wall the induced charge on the wire is

ind

max

)=−N

tot

, which agrees with the statement about the total induced

charge from the previous section. The current induced on the tube (‘the cathode’) is

ind

(t)=−I

ind

(t) since the tube completely encloses the wire and thus the sum of

the two signals must be zero at any time.

As an illustration, in Fig. 5.7 we plot the time development of a current pulse

described by Eqs. (5.18) and (5.19) using typical parameters for a,b, and t

.One

observes the extremely sharp onset and the extremely long tail characteristic of such

pulses.

In a second step we reﬁne the picture by involving the radial extent of the

avalanche, the electron movement, and the ﬁeld dependence of the ion mobility.

We use the model from Sect. 4.4.1, where the Townsend coefﬁcient was taken to be

proportional to the electric ﬁeld (

=(ln2/

V)E) and the ﬁrst multiplication starts

at a minimum ﬁeld E

min

. With E

min

= U/(r

min

ln(b/a)), the number of electrons

present at distance r is given by

N(r)=exp





min

(r)dr





min



U ln2

V ln(b/a)

(5.20)

The total number of avalanche electrons (the gain) is N

tot

= N(a). The number

of electrons created between r and r + dr is n(r)dr =(dN/dr)dr, so the centre of

gravity r

cog

of the electron avalanche is given by

cog

tot



min

rn(r) dr = a(1 +

)

V ln(b/a)

U ln2

(5.21)

Typical operating voltages U of ≈ 2kV,

V values of ≈ 20V, and ln(b/a) values

of ≈ 10 result in a value for

of the order of 0.1. With traditional wire radii of

a = 10−30

m we ﬁnd that the centre of gravity of the electron avalanche is only a

few micrometers above the wire surface.

With such a small distance to travel to their destination, the wire surface, the

electrons can only make a small contribution to the total signal charge. The latter

Fig. 5.7 Current signal

according to (5.18) ( full

line, left-hand scale) for

= 1.25 ns, b/a = 500, and

q = 10

elementary charges.

Time integral (5.19) of this

pulse as a percentage of the

total (broken line, right-hand

scale)

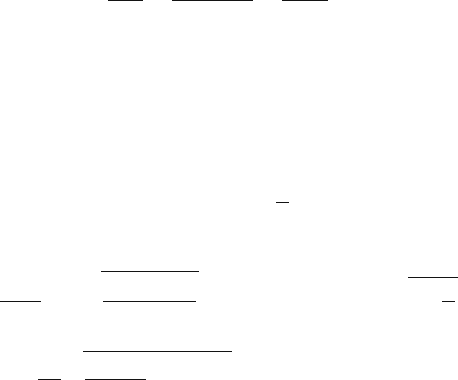
5.6 Signals Induced on Electrodes Connected with Impedance Elements 165

one is given by Q

ind

tot

= −e

tot

once all the electrons and ions have arrived on

their respective electrodes (see the previous section). The signal from the electrons

may be calculated using Eq. (5.14), which tells us that a single electron moving

from distance r to the wire surface induces a charge of −(e

/ )(

(a) −

(r)) =

−e

ln(r/a)/ ln(b/a). Thus, assuming that all the electrons are moving from r

cog

the wire surface, the fraction of charge induced by the avalanche electrons is given

ind

tot

ln(r

cog

/a)

ln(b/a)

≈

U ln2

. (5.22)

For typical values of U and

V discussed above, the fraction of charge induced

by the movement of the electrons amounts to 1 or 2% of the total induced charge.

Since the electrons arrive at the wire within a time much shorter than 1 ns, for all

practical purposes we can assume the electron component of the signal to be a delta

current I

ind

(t)=Q

ind

(t). The ions move from their point of creation to the tube

wall, and we assume here that they all start from r

cog

. In the high electric ﬁelds of

–10

V/(cm Torr) in the vicinity of the wire, the ion velocity is not proportional

to E but rather is related to the ﬁeld by v =

√

E (Sect. 2.2.2). Thus, for the early

part of the ion trajectory we have

dr(t)

r(t)ln(b/a)

→ r(t)=a(1+

)



ln(b/a)

(1+

)

. (5.23)

In practice, t

is a small factor (say two or three times) larger than t

. It is remarkable

that the functional dependence on t is the same as the one of the simpliﬁed case of

Eq. (5.16). The reﬁnements have only changed the numerical values of t

and a,so

the signal again assumes a hyperbolic form with a characteristic time constant t

The sharp onset and the long tail remain as shown in Fig. 5.7.

Since the electric ﬁeld in the vicinity of the wire of any wire chamber has the

form 1/r, the universal shape of the induced current signal I

ind

(t) Eq. (5.18) is valid

for wire signals of all wire chamber geometries.

5.6 Signals Induced on Electrodes Connected

with Impedance Elements

In this section we calculate the signals induced by moving charges on electrodes

connected with arbitrary impedance elements. Before doing this, however, we ﬁrst

investigate the circuit shown in Fig. 5.8, where external current sources I

are

impressed on nodes which are connected to impedances Z

. These impedances

represent linear ‘physical’ objects such as resistors, capacitors, and ampliﬁers. In

the Laplace domain (see Chap. 6), the current I

ﬂowing from node n to node m

166 5 Creation of the Signal

Fig. 5.8 Circuit diagram

representing three nodes

connected to each other and

ground through impedances

.TheI

(t) represent

external currents impressed

on the nodes, and the

(t) represent the resulting

voltages

(t)

through Z

and the current I

ﬂowing between node n and ground through Z

are

deﬁned by

(s)=[V

(s) −V

(s)]/Z

(s) and I

(s)=V

(s)/Z

(s). (5.24)

On every node, the sum of all currents must be zero, which gives

−I

−

∑

m=n

= 0 → I

∑

, (5.25)

where we have deﬁned the admittance matrix y

of the circuit as

∑

= −

n = m. (5.26)

The voltages on the nodes, resulting from the impressed currents, are therefore

given by

(s)=

∑

(s)I

(s) z

(s)=y

−1

(s). (5.27)

The matrix z

is the inverse of the admittance matrix and is called the impedance

matrix of the circuit.

Up to this point we have understood that there is a linear relationship [Eq. (5.25)

or Eq. (5.27)] between the currents I

(t) impressed on the nodes of the network

(Fig. 5.8) and the resulting potentials V

(t) on the nodes. What we ﬁnally want

to determine are the potentials V

ind

(t) induced by a moving charge q between the

electrodes that are part of a network as shown in Fig. 5.9a. In the following we

will ﬁnd that these voltages are calculated by adding the mutual electrode capaci-

tances to the network from Fig. 5.8 and placing the currents that would be induced

on grounded electrodes as impressed currents to this circuit (Fig. 5.9b). The drift

of charges in gases is slow enough to allow the use of the quasi-electrostatic cal-

culation, meaning that Eq. (5.5) and the reciprocity theorem (5.7) are also valid for

time-dependent charges Q

(t) and voltages V

(t) at every time t. Following the pro-

cedure of Sect. 5.3, we use a second electrostatic state, where

(t)=0, V

(t)=V

and V

(t)=V

(t)=0, which gives