Blum W., Riegler W., Rolandi L. Particle Detection with Drift Chambers

Подождите немного. Документ загружается.

136 4 Ampliﬁcation of Ionization

Table 4.2 Measured Diethorn parameters for various gases

Gas mixture E

min

(

)

V Refs.

(k V/cm) (V)

Ar(90%)+CH

(10%) 48± 323.6±5.4HEN72

Ar(95%)+CH

(5%) 45± 421.8±4.4HEN72

69± 536.5 ±5.0HEN72

100± 429.5±2.0HEN72

He(96%)+(CH

)

CHCH

(4%) 148± 227.6±3.0HEN72

Ar(75%)+Xe(15%)+CO

(10%) 51± 420.2±0.3HEN72

Ar(69.4%)+Xe(19.9%)+CO

(10.7%) 54.5 ± 4.0 20.3 ±2.5HEN72

Ar(64.6%)+Xe(24.7%)+CO

(10.7%) 60± 518.3±5.0HEN72

Xe(90%)+CH

(10%) 36.2 33.9 WOL 74

Xe(95%)+CO

(5%) 36.6 31.4 WOL 74

(99.8%)+Ar(0.2%) 171 38.3 KIS 60

Ar(92.1%)+CH

(7.9%) 77.5 30.2 DIE 56

(76.5%)+Ar(23.5%) 196 36.2 DIE 56

(90.3%)+Ar(9.7%) 21.8 28.3 DIE 56

Ar(90%)+CH

OH(10%) 62 27.0 DIE 56

144 40.3 DIE 56

4.4.2 Dependence of the Gain on the Gas Density

The variation of the gain with the gas density is of particular interest since very

often the chambers are operated at atmospheric pressure and the gas density changes

proportionally to it. From (4.10) and (4.11), a small relative change d

of the

density can be seen to result in a change of ampliﬁcation of

= −

ln2

πε

. (4.15)

In practical cases the factor that multiplies d

ranges between 5 and 8: varia-

tion of the gas pressure causes global variations of the gain that are typically 5 to 8

times larger. Since the gas pressure can be easily monitored these variations can be

corrected for.

4.4.3 Measurement of the Gain Variation with Sense-Wire

Voltage and Gas Pressure

In this section we give some measurements of the variation of the gain with the

sense wire voltage and with the atmospheric pressure. These measurements have

been obtained using prototypes of the ALEPH TPC that had a cell geometry as

described in Sect. 3.2.

Figure 4.10 shows a plot of the gain as a function of the voltage (cf. (4.14)) using

the Diethorn parameters for an Argon (90%)–CH

(10%) mixture (cf. Table 4.2) and

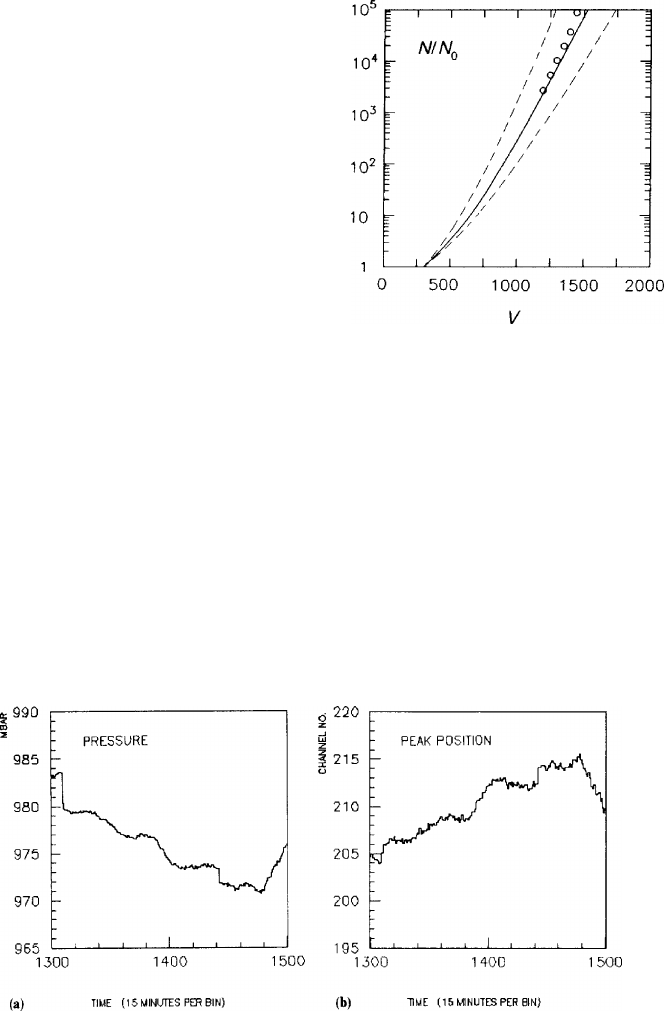
4.4 Ampliﬁcation Factor (Gain) of the Proportional Wire 137

Fig. 4.10 Gain as a function

of the sense-wire voltage in a

chamber with a cell geometry

as described in Sect. 3.2. Dots

are measurements done with

a model of the ALEPH TPC;

the full line is computed with

(4.14) and Table 4.2; broken

lines show the error margins

introduced by the error in

Table 4.2

assuming atmospheric pressure. The two side-lines show the large uncertainty in

the prediction of the gain owing to the large error (20%) in

V. The superimposed

experimental points have been measured with a chamber under the same operating

conditions. The agreement is very good.

Figure 4.11 shows the variation of the atmospheric pressure p over a period of

2 days (a) and the corresponding average pulse height measured by the chamber

when detecting the electrons produced in the gas by the absorption of X-rays from

Fe source (b). One notices how the measured pulse height follows the variations

of the pressure (note the zero-suppressed scales of the two plots). The chamber

was operated in an Argon (90%)–CH

(10%) mixture. The sense-wire voltage was

1.4 kV and the ﬁeld wires were grounded. Using Table 3.5 we can compute the

linear charge density

of the sense wires and from the measured value of

Fig. 4.11 (a) Atmospheric pressure p as a function of the time in a time interval of two days. (b)

Average pulse-height measured by the chamber in the same period. Measurements done with the

ALEPH TPC

138 4 Ampliﬁcation of Ionization

(cf. Table 4.2) using (4.15) we predict that

= −(6.7±1.5)

Inspecting Fig. 4.11 a we read an overall change of pressure of 0.8% and predict a

change of gain of −(5.5 ±1.2)%, in agreement with the variation (−4%) shown in

Fig. 4.11b.

4.5 Local Variations of the Gain

Equation (4.12) shows that the gain depends on the local charge density of the wire

. A relative change d

, as may result from geometrical imperfections of a wire

chamber, from ﬂuctuations of the supply voltage, or from space charge near the wire

will change the ampliﬁcation by the factor [cf. (4.12)]



lnG +

ln2

πε



. (4.16)

In practical cases the two factors in the parentheses of the previous equation are of

the same order of magnitude and their sum lies in the range 10–20: the local relative

variations of the charge density cause local relative variations of the gain that are

typically 10–20 times greater.

In Sect. 3.2 we saw how the linear charge density

depends on the potentials

and on the geometry of the wire chamber, assuming that there is an ideal geometry.

Real chambers deviate from the ideal geometry: the wires are not inﬁnite and we

can expect changes in the charge density in the region close to the wire supports.

Moreover, the mechanical components of the chamber have small construction im-

perfections, which can induce local changes in the charge density along the wire.

The mathematical solution of the electrostatic problem is not simple because as

soon as we introduce variations in the ideal geometry we lose the symmetry of the

boundary conditions.

In drift chambers that are operated in high-density particle ﬂuxes there is another

problem: the local charge density on the wire seen by ionization electrons when they

reach the wire can be modiﬁed by the presence of the ions which were produced in

a previous avalanche and still are drifting inside the drift cell.

4.5.1 Variation of the Gain Near the Edge of the Chamber

In wire chambers the gain usually drops to zero near the support frame. This be-

haviour depends on the details of the geometry and extends over a region of the

wire comparable to the distance between the sense-wire grid and the cathode plane.

4.5 Local Variations of the Gain 139

Fig. 4.12 Measured pulse heights of wire signals created by a laser beam near the wire support

frame as a function of the distance between the frame and the laser beam. Guard strips can extend

the sensitive length of the wire. The distance between neighbouring grids was 4 mm [BRA 85]

Figure 4.12 from [BRA 85] shows the relative variation of the gain near the edge of

a wire chamber.

The dependence of the wire gain on the distance from the chamber edge can be

modiﬁed by the addition of ﬁeld correction strips [BRA 85], [AME 86c], which can

be trimmed to an appropriate voltage to modify the electric ﬁeld in the region of the

frame and to obtain a more uniform charge density (see Fig. 4.12).

4.5.2 Local Variation of the Gain Owing to Mechanical

Imperfections

Here we want to evaluate the extent to which small deviations from the ideal ge-

ometry can affect the charge density on the sense wires, and we refer again to the

example discussed in Sect. 3.2. The problem has been extensively studied by Erskine

[ERS 72], and we refer to his paper for a general discussion.

The order of magnitude of the charge variation induced by some imperfections of

the chamber can be obtained using the general formulae of Sect. 3.2: this is possible

for imperfections that can be approximated to a large extent as a global variation of

the geometry of the chamber. For example, the effect of a bump in the cathode plane

can be evaluated from the global effect of a reduction of the distance between the

sense-ﬁeld grid and the cathode plane.

In the following we refer to the notation of Sect. 3.2 and to the geometry sketched

in Fig. 3.4. Equation (3.39) gives the potentials of the electrodes as a function of

140 4 Ampliﬁcation of Ionization

their charges and of the matrix of the potential coefﬁcients A:

V = A

, (4.17)

where the

are the linear charge densities on the wires of each grid divided

by the pitch of the grid. A change in the geometry of the wire chamber induces a

change in the matrix. Differentiating (4.17) with the ﬁxed values of the potential V,

we obtain

= −dA

where d

is the vector of the charge-density variations and dA is the matrix of

the variations in the potential coefﬁcients induced by a particular change in the

geometry of the chamber. Using the previous equation, we obtain

= −A

−1

. (4.18)

As a ﬁrst example we calculate the charge-density variation induced by a dis-

placement of the cathode plane. The matrix dA can be calculated by differentiating

(3.41) with respect to z, noting that the effect of a displacement dz of the cathode

plane changes z

and z

by the same amount (cf. Fig. 3.4):

dA = −

⎛

⎜

⎝

111

⎞

⎟

⎠

. (4.19)

From (4.18),

−1

⎛

⎜

⎝

⎞

⎟

⎠

. (4.20)

In the approximations of Sect. 3.2 the quantity

is the charge density

on the cathode plane. The charge-density variation d

induced by a displacement

of the cathode plane vanishes if there are no charges on the plane. In the particular

geometry of the example considered in Sect. 3.2, we obtain:

=(70m)

−1

dz(

As another example we now compute the charge variation induced by a change in

the sense-wire diameter. Differentiating (3.41) with respect to the sense-wire radius

yields

dA = −

πε

⎛

⎜

⎝

100

000

⎞

⎟

⎠

, (4.21)

4.5 Local Variations of the Gain 141

and

= −

πε

−1

⎛

⎜

⎝

⎞

⎟

⎠

. (4.22)

For the particular example considered in Sect. 3.2 we get

= 0.16

The effect of the displacement of a single wire is more difﬁcult. In this case we

cannot use (3.41) because it was calculated for a set of symmetric grids, and this

symmetry is lost when a single wire is displaced. We note that in ﬁrst order the

displacement of a wire does not affect the charge density of the wire itself (again

because of the symmetry), but only that of other wires close to it. The displacement

of a ﬁeld wire changes the charge density of the two closest sense wires proportion-

ally to its own charge density. If there is no charge density on the ﬁeld wires, their

displacement does not affect the gain of the chamber.

Table 4.3 shows the gain variations induced by mechanical imperfections in the

geometry of the example discussed here. We have assumed that the setting of the

voltages produces a gain of 10

, and using (4.16) we compute the relation between

the relative variation of the gain and the local relative charge-density variation:

=(15.9±1.5)

The same gain can be obtained for different settings of the sense-wire voltage

) and the ﬁeld-wire voltage (V

) that leave the charge density on the sense wire

unchanged. Using Table 3.3 we compute the condition of constant gain:

0.25V

−0.11V

= constant.

The different settings correspond to different values of the ratio

. Again using

Table 3.3 we deduce that if V

= 0, then

= −0.44, while

= 0 when

= 0.34. As shown in Table 4.3 the ratio

inﬂuences the local variations

of the gain that are due to mechanical imperfections.

Table 4.3 Gain variation dG/G induced by mechanical imperfections in the geometry discussed

in Sect. 3.2. A gain of 10

is assumed and all displacements (

) are in mm.

is the ratio

between the charge densities on the ﬁeld wires and the sense wires

Imperfection dG/G

Bump on the pad plane 0.69

z(1+

)

Displacement of a ﬁeld wire 1.1

Displacement of a sense wire 0.2

Variation of the sense wire diameter 2.5

r/r

142 4 Ampliﬁcation of Ionization

4.5.3 Gain Drop due to Space Charge

When the avalanche has come to an end, all electrons are collected on the anode and

the space near the wire is ﬁlled with the remaining positive ions. We may assume

that in the regime of proportional wire ampliﬁcation, the amount of charge in the

avalanche is small compared to the charge on the wire (integrated along the wire

over the lateral extent of the avalanche). The positive ions are moving away from

the wire at relatively low speed. With a mobility of a few cm/s per V/cm, a typical

speed near the thin wire (E ∼ 2 ×10

V/cm) would be several 10

cm/s, and a

hundred times less at a hundred times the radius. The avalanche charge obviously

takes hundreds of microseconds to settle on a cathode several millimetres away.

When there is a continuous particle ﬂow with a much higher frequency than that

corresponding to the ion travel time, we have a stationary situation, and the travel-

ling ions build up a stationary space charge density

(x) in the chamber volume.

This reduces the electric ﬁeld close to the wire and therefore the gas gain, which

poses a fundamental limitation on the rate capability of any wire chamber.

In order to calculate

we consider in Figure 4.13 a small area A

of the wire

surface which shows an electric ﬁeld E

and which releases positive ions of charge

q at a constant rate

. The ions are moving with a velocity of v =

where

the ion mobility. Within a time

t, the charge Q

= q

νΔ

t is entering the volume

= A

t, which results in a charge density of

= Q

= q

close to

the wire surface. As the ions are moving away from the wire along the electric ﬁeld

lines they are passing an equipotential area A

in a ﬁeld E

, and the charge density

at this position is

= q

. From Gauss’ Law we know that E

−E

, where Q is the total charge contained in the ‘ﬂux tube’ between A

and A

If the electric ﬁeld due to the space charge is small compared to the electric ﬁeld

A1, E1

A2, E2

A3, E3

Fig. 4.13 Anode wire with some ﬁeld lines (continuous) and some equipotential lines (broken).

The A’s symbolize the areas of the equipotential surfaces between the same ﬁeld lines that come

from the border of the original area A

on the wire surface. The E’s represent the ﬁelds on the

equipotential surfaces. As the ions travel along the ﬁeld lines they become slower by the same

factor as the ﬁeld lines go apart, resulting in a constant charge density in the volume (‘ﬂux tube’)

ﬁlled with ions originating from A

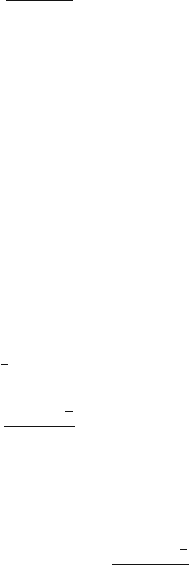
4.5 Local Variations of the Gain 143

from the wire, which is usually the case, we may neglect Q and obtain in ﬁrst order

that

= E

and therefore

We have found the remarkable result that the charge density is constant along the

entire ‘ﬂux tube’ at any distance from the wire. In case the electric ﬁeld E

and

the ion ﬂux

are uniform around the wire surface, which is a common case, we

ﬁnd a constant charge density in the entire volume that is ﬁlled by the ﬁeld lines

originating from the wire.

For a wire of radius a with a surface ﬁeld of E

, a charge deposit q at a rate of R

per unit length of the wire we therefore ﬁnd a uniform space charge density of

. (4.23)

Next we investigate the gas gain drop due to the presence of

. Setting a wire to

potential V

amounts to placing a certain charge

on the wire. The charge density

creates an electric ﬁeld E

(x) which is superimposed on the electric ﬁeld of the wire

charge

. The resulting potential difference due to

V =



(x)ds, where the

path of integration is taken from the wire surface to the cathode. Consequently the

wire charge

is reduced such that its contribution to the potential is V

−

V.The

gain reduction due to the space charge

is therefore equal to a voltage reduction

V in the absence of space charge. This effective voltage drop of the wires in a

chamber is therefore calculated in ﬁrst order by removing all wires and calculating

the potential difference between wire positions and cathode due to the charge density

. We will now discuss two examples.

First we examine a drift tube (cf. Section 3.1) exposed to a particle ﬂux of

per

unit detector area and a total avalanche charge of q per particle. With R = 2b

and

the wire surface ﬁeld of E

= V

/(aln

) we ﬁnd the uniform space charge density

πμ

. (4.24)

In the absence of the wire,

produces an electric ﬁeld of E

(r)=

r/2

,sothe

potential difference between wire position and tube wall is

V =



(r)dr =

πε

. (4.25)

The voltage drop is proportional to the third power of the tube radius, so a reduction

of the tube radius is the most effective way to increase the rate capability. As an

example, Fig. 4.14 shows the gain reduction in the drift tubes of the ATLAS muon

spectrometer [ATL 00]. The measurements are well explained by the theory outlined

above.

As a second example we investigate a wire chamber schematically shown in

Fig. 4.15, where a row of wires with a pitch of s is positioned symmetrically be-

tween two grounded cathode planes at a distance h. Setting all wires to potential V

144 4 Ampliﬁcation of Ionization

0.6

0.65

0.7

0.75

0.8

0.85

0.9

0.95

Count rate (Hz/cm)

G/G

worst ATLAS background rate

including safety factor 5

calculation with average

energy deposit 36

keV

measured gain ratio G/G

Fig. 4.14 Calculated and measured gain drop in drift tubes due to photon background in the

ATLAS muon spectrometer. The parameters are b = 15mm, a = 25

m, V

= 3170V,

0.55cm

/Vs. The gain of 2 ×10

and primary charge deposit of 1400 electrons/photon yields

q = 4.5pC. A rate of R = 1000Hz/cm results in a voltage drop

V = −17V and therefore a gas

gain reduction of 10%

the electric ﬁeld on the wire surface is given by E

= V

/alog

where r

is a length

with an average value of the same order of magnitude as s and h. A particle ﬂux of

results in R = s

and we therefore have a uniform charge density of

πμ

. (4.26)

The electric ﬁeld due to the charge density

in the absence of the wires is given by

E(z)=

, and the resulting potential difference is

V =



E(z)dz =

πε

. (4.27)

As before, the voltage drop mainly depends on the chamber dimensions s and h

which must be small for a high rate capability of the wire chamber.

One should be aware of the fact that the ion mobility

is often not known very

well due to the presence of charge transfer in the migration of ions. This was elabo-

rated on the last pages of Sect. 2.2.2.

Fig. 4.15 Multiwire

proportional chamber

Z = h

= 0

4.6 Statistical Fluctuation of the Gain 145

4.6 Statistical Fluctuation of the Gain

The gain of an avalanche is equal to the number of ion pairs within it divided by

the number of electrons that started the avalanche. In the regime of proportionality,

the average number of electrons produced in the avalanche is proportional to the

number of initial electrons. We are interested in the ﬂuctuation in the number of

electrons that is caused by the random nature of the multiplication process.

We may assume that each initiating electron develops its own small avalanche,

independent of the presence of the others nearby. If we want to know the probabil-

ity distribution of the number N of the ions in the total avalanche we simply sum

over the probability distribution P(n) of the number n of electrons in the individual

small avalanches. The ﬁrst step is to ﬁnd an expression P(n), which is done in the

following sections.

If the number k of initiating electrons is large, the central-limit theorem of statis-

tics, which makes a statement about the distribution function F(N) of the sum N,

applies:

N = n

+ n

+ ...+ n

, (4.28)

where each of the independent variables n

has the distribution function P(n).Ifthe

mean of P(n) is called

n and the variance is

, then the central-limit theorem states

that in the limit of k →∞, F(N) is a Gaussian:

F(N)=

√

exp

(

(N −N)

/2S

)

(4.29)

with

N = kn and S

= k

. (4.30)

This means that the exact shape of P(n) is not needed for the distribution of

avalanches started by a large number of electrons. On the other hand, P(n) is par-

ticularly interesting for drift chambers where individual ionization electrons have to

be detected, as in ring-imaging (RICH) counters.

Single-electron spectra and avalanche ﬂuctuations in proportional counters have

been measured by Hurst et al., using laser resonant ionization spectroscopy (RIS)

[HUR 78] and by Schlumbohm [SCH 58], whose data are discussed later. A review

of single-electron spectra is given by Genz [GEN 73].

Statistical ﬂuctuations of the gain may be inﬂuenced by chemical reactions asso-

ciated with the formation of avalanches. Such deterioration of performance occurs

either through deposits on old wires or through the presence of small contaminations

of the gas. A discussion of these effects is given in Sect. 12.6; we refer especially to

Fig. 12.7. Here we assume that the proportional wire is in an unperturbed working

condition.

4.6.1 Distributions of Avalanches in Weak Fields

In this section we investigate the ﬂuctuation of avalanches started by single elec-

trons in weak electric ﬁelds, where the assumption holds that the average distance