Blum W., Riegler W., Rolandi L. Particle Detection with Drift Chambers

Подождите немного. Документ загружается.

5.7 Signals Induced in Multiwire Chambers 177

Γ(λ)

Gauss

Gatti

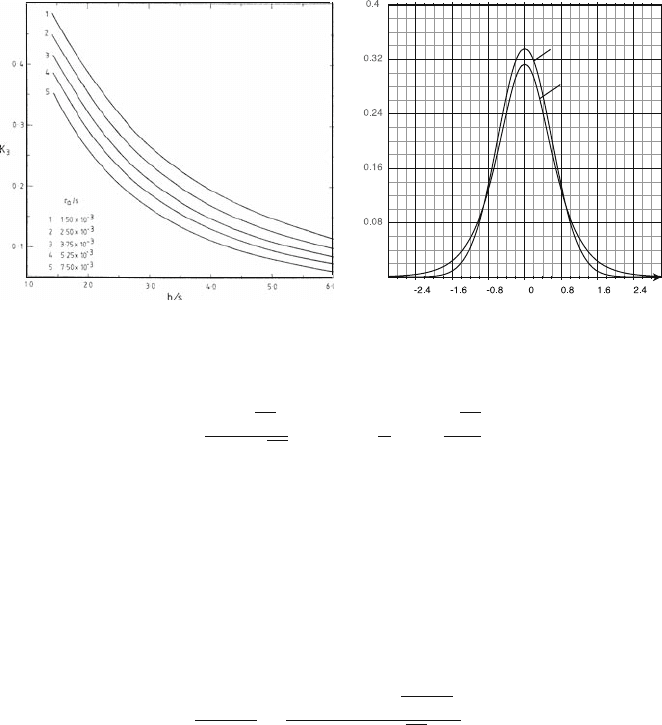
Fig. 5.15 (a) Values of the parameter K

as a function of chamber geometrical parameters h/s

and a/s [MAT 84b]. (b) Cathode charge distribution

(

) according to Gatti for h/s = 2and

a/s = 5.25×10

−3

together with a Gaussian that has the same area and the same FWHM

√

4atan

√



1−

√



. (5.58)

(

) represents the charge distribution on one of the cathode planes originating

from a single avalanche. We take it to be independent of direction in that plane,

the variable

= x/h representing one coordinate in that plane, normalized to the

anode-cathode distance h. The other coordinate, at right angles to x, has already

been integrated over, following the idea of a cathode segmented into strips. One

of the two curves in Fig. 5.15b is Eq. (5.57) with a choice of K

indicated in the

caption. The other is a Gaussian for comparison, with the same area and the same

width. Gatti’s curve has a longer tail at large |

|. The FWHM of the distribution can

be expressed as

FWHM

4arctanh(1/

√

2+ K

)

(1−0.5

√

)

. (5.59)

Expression (5.57) is approximate in the sense that it neglects any inﬂuence of the

avalanche position around the wire if the avalanche develops on one side. But this

is not relevant unless electric signals are recorded that are so long that the ions have

moved beyond a few wire radii. In practical measurements of particle tracks there

are many avalanches that contribute to an electric signal. These are spread out along

the track, by diffusion and other effects (cf. Chap. 2). The average formula (5.57) is

then quite adequate to generate, perhaps in a simulation program, the true charge by

superposition of many

(

) at the avalanche positions

Precision measurements of charge distributions for different avalanche positions

around the wire were reported by Gordon and Mathieson [MAT 84a].

Varying the ratio of cathode separation to wire pitch h/s from 0.1 to ∞, the para-

meter K

assumes values between 0.1 and 1, which means that the FWHM assumes

values between 2.8h and 2.4h. For a strip of ﬁnite width w centred at position

,we

get the signal I(t,

,w) by integrating Eq. (5.56), and we ﬁnd

178 5 Creation of the Signal

I(t,

,w)=



+w/2

−w/2

(t,



= I

(t)



+w/2

−w/2

(



= I

(t) P

(

), (5.60)

where

(

√



arctan





tanhK

(

)



−arctan





tanhK

(

−

)



(5.61)

We call P

(

) the pad response function. The fact that the signal on the entire

cathode plane is equal to half the total cathode signal is veriﬁed by evaluating

lim

w→∞

(

. (5.62)

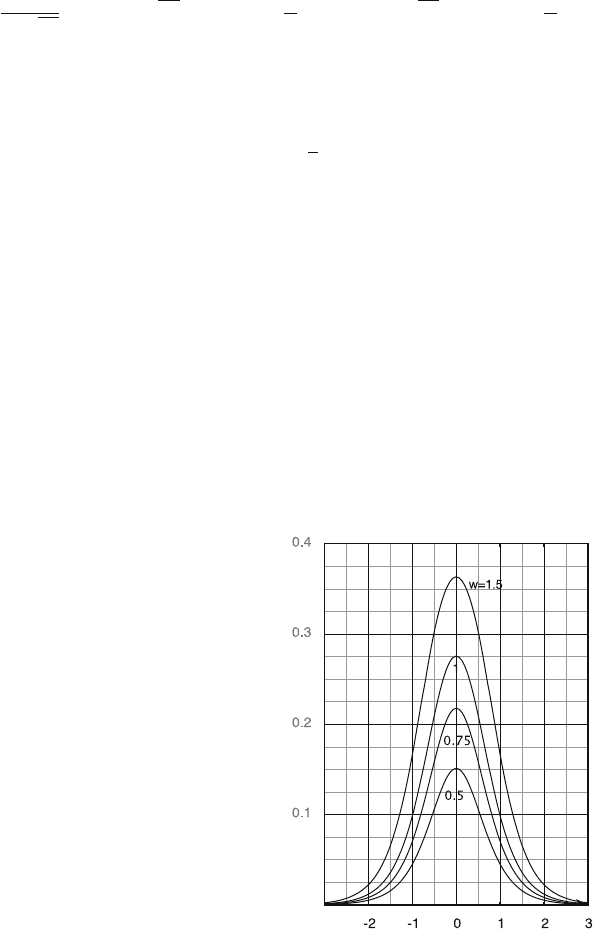
The pad response function depends on the strip width w. Figure 5.16 shows some

examples calculated for various w’s using the charge distribution displayed in

Fig. 5.15. The pad response function determines what fraction of the total cath-

ode signal is induced in the strip as a function of the distance between the centre

of the strip and the avalanche position (measured in the cathode plane). Equation

(5.62) implies that this fraction would reach 50% for an inﬁnitely wide strip. For

narrower strips it is still quite large, the example of Fig. 5.16 shows that 22% is

collected when the avalanche is at the centre of a strip with width 0.75h and 11%

if it is over the centre of the neighbouring strip. For the measurement of tracks an

effective pad response function P

eff

(

) is applicable, which results from folding in

the distribution of the positions of avalanches that contribute to the cathode strip

signal. This P

eff

(

) can either be constructed using the methods described above

Fig. 5.16 Pad response

functions for four different

strip widths w in units of the

anode cathode distance h.

As w decreases, the curves

become smaller and thinner

(λ

)

References 179

or be measured by ﬁtting tracks. Often a simple superposition of Gauss curves is

sufﬁcient.

The measurement of the coordinate of the avalanche is made by interpolating

the signals recorded on adjacent cathode strips with the help of the effective pad

response function P

eff

(

). The strip width w and the cathode distance h have to be

chosen such that the typical pulse height induced on two or three adjacent strips falls

into the dynamic range of the readout electronics. If the resolution limit for position

determination along the wire is given by the electronics pulse-height measurement, a

strip width near the cathode-anode distance (w ≈h) gives the best position resolution

[GAT 79]. When the coordinate of the avalanche is exactly in between two strips, it

induces two equal signals on them. If the avalanche is produced in correspondence

with the centre of one strip, it induces a large signal on it and two smaller signals on

the two adjacent strips. Typically one records two signals in the ﬁrst case and three

in the second.

Measuring the signal I

(t) and I

(t) on two adjacent cathode strips of pitch w we

have the relations I

(t)/I

(t)=P

(

)/P

(

−w), which can be inverted to yield the

avalanche position

. Measuring the signals on three adjacent strips over-constrains

the equation and leads to a further improvement of the position resolution. With

(t)

= p

(

)

(

−w)

(t)

= p

(

)

(

+ w)

(5.63)

we ﬁnd

and

which determines the same avalanche position. Since the mea-

surement error is roughly inversely proportional to the recorded pulse height on the

outer strips, one may use the relative weights of p

and p

to estimate

from the

two independent measurements

+ p

) (5.64)

In order to achieve a precise signal measurement, the readout electronics will use

a signal processing ﬁlter that optimizes the signal-to-noise ratio. Such a processing

chain leaves the ratio of signals on neighbouring strips unchanged as long as it is

the same for the strips involved.

Another common way of determining the avalanche position is to simply deter-

mine the centre of gravity of the strip charges or to apply a Gaussian type ﬁt to the

measured charges [END 81]. All of these methods introduce systematic errors as a

function of the distance of the track from the strip centre (‘differential nonlinearity’),

but these can be corrected with suitable models.

References

[CHA 92] G. Charpak, Electronic Imaging of Ionizing Radiation with Limited Avalanches in

Gases, Nobel Lecture, Stockholm, December 8, 1992

[END 81] I. Endo et al., Systematic shifts of evaluated charge centroid for the cathode readout

multiwire proportional chamber, Nucl. Instr. Meth. Phys. Res. A 188, 51–58 (1981)

180 5 Creation of the Signal

[GAT 79] E. Gatti et al., Optimum geometry for strip cathodes or grids in MWPC for avalanche

localization along the anode wires, Nucl. Instr. Meth. Phys. Res. A 163, 83–92 (1979)

[GAT 82] E. Gatti, G. Padovini, V. Radeka, Signal evaluation in multielectrode radiation detec-

tors by means of a time dependent weighting vector, Nucl. Instr. Meth. Phys. Res. A

193, 651–653 (1982)

[JAC 75] See any introduction to electrostatics, for example J.D. Jackson, Classical Electrody-

namics, Ch. 2, 2nd edition (John Wiley and Sons. New York 1975)

[MAT 84a] J.S. Gordon and E. Mathieson, Cathode charge distributions in multiwire chambers, I.

Measurement and theory, Nucl. Instr. Meth. Phys. Res. A 227, 267–276 (1984)

[MAT 84b] E. Mathieson and J.S. Gordon, Cathode charge distributions in multiwire chambers,

II. Approximate and empirical formulae, Nucl. Instr. Meth. Phys. Res. A 227, 277–282

(1984)

[RAM 39] S. Ramo, Currents induced in electron motion, Proc. IRE 27, 584 (1939)

[RIE 04] W. Riegler, Extended theorems for signal induction in particle detectors, Nucl. Instr.

Meth. Phys. Res. A 535, 287–293 (2004)

[SAN 80] R. Santonico and R. Cardarelli, Development of Resistive Plate Counters, Nucl. Instr.

Meth. Phys. Res. A 187, 377–380 (1981)

Chapter 6

Electronics for Drift Chambers

The signals induced on the drift chamber electrodes must be processed by appro-

priate readout electronics. The design and speciﬁcation of the electronic circuits

depend strongly on the detector application. For timing purposes one typically wants

fast ampliﬁers to reduce time walk effects. For applications where charge measure-

ment is required one prefers long integration times (slower ampliﬁers) in order to

integrate a large fraction of the detector signal. For high-rate applications, signal

tail cancellation and baseline restoration are important issues in order to avoid sig-

nal pileup and baseline ﬂuctuations. The electronics noise level must be considered

as well as it determines the required chamber gas gain for the desired signal-to-noise

ratio.

The art and science of electronics is a universe of its own, and we cannot develop

the contents of this chapter from the basic principles as we have undertaken to do in

the other chapters of this book. Here it is our task to collect the concepts that allow

us to arrive at the electronics speciﬁcations for particular detector applications. The

numerous ways of realizing the actual circuits are also not part of this book. The

reader interested in a more detailed treatment of electronic signal processing may

want to consult the textbooks of Oppenheim and Willsky [OPP 97] (mathematical

tools), Nahvi and Edminster [NAH 03], Horowitz and Hill [HOR 89] (basic intro-

duction to electronic circuits), Nicholson [NIC 73] (nuclear electronics), Radeka

[RAD 88] (low noise techniques), and Rehak [REH 83] and Gatti [GAT 85] (signal

processing for particle detectors).

The front-end electronics of wire chambers, or at least their ﬁrst stages, are typ-

ically linear signal processing devices. A linear signal processing device has the

property that a given input pulse shape I

(t) results in an output pulse shape V

out

(t)

which is independent of the signal amplitude, i.e., V

out

[c ×I

(t)] = c ×V

out

(t)]

for any value of the constant c.

There are important advantages of linearity: in position-sensitive wire cham-

bers with cathode segmentation for cathode charge interpolation (Sect. 5.7.2), the

track position is determined by the ratio of the charges induced on neighbouring

strips or pads. If the readout electronics were nonlinear, one would have to apply

a pulse-height-dependent correction of the position, which is undesirable. Another

W. Blum et al., Particle Detection with Drift Chambers, 181

doi: 10.1007/978-3-540-76684-1

 Springer-Verlag Berlin Heidelberg 2008

182 6 Electronics for Drift Chambers

compelling reason for linearity is related to signal shaping. The long 1/(t + t

) tail

of the wire chamber signal leads to signal pileup and hence to rate limitations. For

this reason one introduces ﬁlters (shapers) which reduce the pulse width. If the am-

pliﬁer stages preceding the shaper are nonlinear, the signal shapes arriving at the

shaper vary according to their amplitude, which makes the shaper circuit with ﬁxed

parameters inefﬁcient. For linear electronics the shaper just has to be matched to the

input pulse shape, i.e., to the parameter t

for the given wire chamber geometry.

An ampliﬁer is traditionally considered a device that produces an ampliﬁed copy

of the input signal. For example, the output of an ideal voltage ampliﬁer for an

input voltage signal v

(t) is v

out

(t)=G ×v

(t), where G is the (dimensionless)

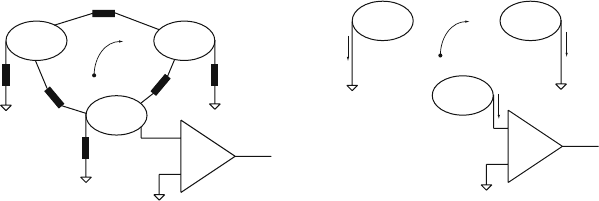
voltage gain of the ampliﬁer. Figure 6.1a shows how a voltage signal induced on a

detector electrode is read out by a voltage ampliﬁer. In order to create an exact copy

of the induced voltage signal the input impedance of the voltage ampliﬁer must be

inﬁnite, because for ﬁnite input impedance we would ﬁnd a current ﬂowing into the

ampliﬁer, which would change the voltage V

(t).

Figure 6.1b shows a set of grounded electrodes where the moving charge in-

duces currents. Such a current can be read out by an ideal current-sensitive ampliﬁer,

which produces an output voltage signal v(t)=ki

(t). The ‘gain’ k has the dimen-

sion of

and it would be more precise to call this device a current-to-voltage

converter. The input impedance of the device must be zero so that the electrodes

stay at ground potential.

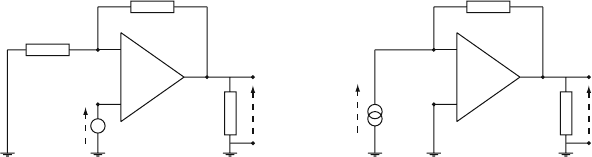
Figure 6.2 shows the realization of voltage and current ampliﬁers using an op-

erational ampliﬁer, which is a device with very high voltage gain, very high input

impedance, and very high bandwidth, ideally all being inﬁnite. The voltage am-

pliﬁer shown in Fig. 6.2a has a gain of G = V

= 1 + R

and inﬁnite input

impedance. The output voltage V

is independent of the load R

. The current ampli-

ﬁer shown in Fig. 6.2b has a gain of k = V

= −R and zero input impedance. Also

for this device the output voltage V

is independent of the load R

.Ifwewerejust

interested in a copy of the induced signal, the electronics chapter of this book would

end at this point. In practice the induced signal must be processed and transformed

by several ﬁlters in order to arrive at a useful signal-to-noise ratio, pulse width,

and frequency spectrum of the output signal, because these quantities determine the

x(t)

(t) V

(t)

V(t)

= GV

(t)

V(t)

= kl

(t)

= ∞

= 0

a) b)

Fig. 6.1 (a) An ideal voltage ampliﬁer with gain G and inﬁnite input impedance reading the voltage

signal induced on the detector electrode. (b) An ideal current ampliﬁer with conversion factor k

and input impedance zero reading the current signal induced on the detector electrode

6.1 Linear Signal Processing 183

–

(t)

–

(t)

a) b)

(t) V

(t)

Fig. 6.2 Realization of a voltage ampliﬁer (a) and a current ampliﬁer (b) by using an operational

ampliﬁer

charge measurement accuracy, the rate capability, and the crosstalk behaviour of the

detector.

The signal ﬁltering is also called signal shaping, and the readout electronics are

sometimes separated into an ‘ampliﬁer’ and a ‘shaper’. In the following chapters

we only use the word ‘ampliﬁer’ for the entire linear signal processing chain of the

readout electronics.

We conclude this introduction by noting that the vocabulary and tradition in the

ﬁeld of detector electronics is somewhat different from the sometimes more familiar

ﬁeld of radio and telecommunication electronics. Whereas the latter is formulated

almost exclusively in the frequency domain, detector signals are mostly discussed

in the time domain. For detector signals we are interested in pulse height, signal-

to-noise ratio, pulse width, signal pileup, and rate capability. All these numbers

are associated with the amplitude and time dependence of detector signals. In the

frequency domain the effect of a ﬁlter applied to a signal is simply the product of the

signal and the ﬁlter transfer function. The equivalent operation in the time domain is

the convolution of the input signal with the ampliﬁer delta response. As we discuss

mostly time domain signals we make frequent use of the convolution integral.

Before describing the readout electronics we review the necessary vocabulary

and mathematical tools required for analysis of linear signal processing devices.

6.1 Linear Signal Processing

The Laplace and Fourier transformations of time domain signals are essential tools

for electrical circuit analysis. The following section summarizes the principal re-

lationships and examples that are used for later discussion of the actual front-end

electronics. Details of these techniques can be found in numerous textbooks; we

follow the nomenclature and deﬁnitions given in [OPP 97].

6.1.1 Laplace and Fourier Transforms

The Laplace transform of a time-dependent function f (t) is deﬁned by

L [ f (t)] = F(s)=



∞

−∞

f (t) e

−st

dt, (6.1)

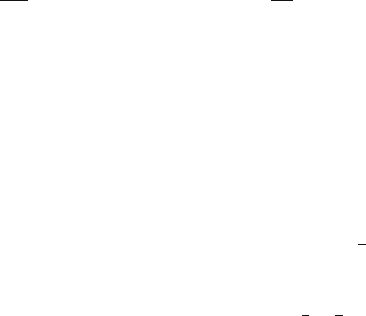
184 6 Electronics for Drift Chambers

where s is a complex number with real part

and an imaginary part

: s =

+ i

This deﬁnition is called the ‘bilateral’ Laplace transform because the integration ex-

tends from −∞ to ∞. In the case where f (t)=0fort < 0 the transform is equal to the

unilateral Laplace transform, which has a lower integration limit of 0. While F(s)

has no direct physical interpretation, the Fourier transform of the signal, deﬁned by

F [ f (t)] =



∞

−∞

f (t) e

−i

dt = F(i

)

= 2

f, (6.2)

expresses the signal as a superposition of sinusoidal waves of frequency f with am-

plitudes |F(i

)| and relative phases arg[F(i

)]. The Fourier transform is a special

case of the bilateral Laplace transform with

= 0. The inverse transforms are

f (t)=



+i∞

−i∞

F(s)e

ds f(t)=



∞

−∞

F(i

. (6.3)

The transformations of the most common functions are tabulated in standard text-

books. For the Laplace and Fourier transforms, the following relations hold (proofs

can be found in [OPP 97]):

(a) Addition (b) Convolution

L [af(t)+bg(t)] = aF(s)+bG(s) L

(



∞

−∞

f (t −t



)g(t



)dt



)

= F(s)G(s)



(n)

(t)



= s

F(s) L

(



−∞

f (t



)dt



)

F(s)

(e) Time shift (f) Time scaling

L [ f (t −t

)] = F(s)e

−st

L [ f (at)] =

)

(g) Damping (h) Multiplication

L [e

−s

f (t)] = F(s + s

) L [t

f (t)] = (−1)

(n)

(s)

(i) Initial value if f (t)=0fort < 0 (j) Final value

f (0

)=lim

s→∞

sF(s) f (∞)=lim

s→0

sF(s)

(k) Parseval’s theorem



∞

−∞

f (t)

dt =



∞

−∞

|F(i2

f )|

df = 2



∞

|F(i2

f )|

(6.4)

The usefulness of these transformations for electrical circuit analysis is illustrated

by the following example. The voltage v

(t) across a resistor R for an impressed cur-

rent i(t) is given by Ohm’s law as v

(t)=Ri(t). The voltage across a capacitor C for

an impressed current i(t) is v

(t)=1/C



i(t)dt. The voltage across an inductance

L for an impressed current i(t) is given by v

(t)=Ldi(t)/dt. Voltages and currents

in a circuit containing R,L, and C elements are determined by applying Kirchhoff’s

laws, which state that the sum of voltages in every loop must be zero and the sum

of the currents on every node must be zero. This analysis therefore leads to a set of

linear differential equations for the currents and voltages in the circuit.

6.1 Linear Signal Processing 185

Writing the above relations in the Laplace domain, we ﬁnd V

(s)=RI(s),

(s)=I(s)/sC, and V

(s)=sLI(s), and the circuit relations become algebraic

equations. Instead of having to solve a set of coupled differential equations in the

time domain we just have to solve a set of linear algebraic equations in the Laplace

domain! In addition, owing to the theorems stated above, many signal manipulations

are strongly simpliﬁed when working in the Laplace domain.

Finally we deﬁne the impedance Z(s) of a circuit element as Z(s)=V(s)/I(s).

We ﬁnd the impedance of Z

(s)=1/sC for a capacitor and Z

(s)=sL for an in-

ductor. In analogy to the resistance R

+ R

of two resistors switched in series, the

total impedance of two impedances Z

and Z

switched in series is Z

+ Z

.Like-

wise, the parallel application of the impedances gives a total impedance of Z

+ Z

6.1.2 Transfer Functions, Poles and Zeros, Delta Response

We now want to read out the chamber output signal i(t) with a general linear signal

processing device. Such a signal is, e.g., the current signal i(t) of the drift tube

indicated in Fig. 5.10. A linear device is deﬁned by the following property: if the

input signals i

(t) and i

(t) result in output signals v

(t) and v

(t), the input signal

i(t)=c

(t)+c

(t) will result in the output signal v(t)=c

(t)+c

(t).

The input and output signals of a linear, time-invariant, and causal device are

related by a differential equation of the following form:

v(t)+a

dv(t)

+ ...+ a

v(t)

= b

i(t)+b

di(t)

+ ...+ b

i(t)

, (6.5)

where the coefﬁcients a and b are independent of time. The term ‘time-invariant’

describes the fact that the relation between input and output signals is independent

of time. For a ‘causal’ system the output signal v(t) is zero as long as the input

signal i(t) is zero.

Performing the Laplace transform and using Eq. (6.4c) transforms this equation

into an algebraic equation with the solution

V(s)=

+ b

s + ...+ b

+ a

s + ...+ a

I(s)=W(s)I(s), (6.6)

where we have deﬁned L [i(t)] = I(s) and L [v(t)] = V(s). The function W(s) is

called the transfer function of the system and we see that the transfer function of a

linear time-invariant system can be expressed by the ratio of two polynomials in the

Laplace domain.

Setting s = i

yields the transfer function in the Fourier domain and the relation-

ship between input and output signals is

V(i

)=W(i

)I(i

). (6.7)

186 6 Electronics for Drift Chambers

Separating the signal I and the transfer function W into the absolute value and the

phase indicates how the frequencies contained in the input signal are separately

transformed in order to yield the output signal:

V(i

)=|I(i

)||W(i

)|exp [iarg[I(i

)] + iarg[W (i

)]]. (6.8)

The sinusoidal components of the input signal I are scaled by |W| and phase shifted

by arg[W]. For very high frequencies the transfer function from Eq. (6.6) behaves as

|W(i

)| =∝

n−m

. (6.9)

A system where n > m is non-physical because it would result in inﬁnite ampliﬁ-

cation at inﬁnite frequency. We can therefore state that for the transfer function of

a realistic linear device we have n ≤ m.Annth-order polynomial has n (real and

complex) roots, so the transfer function W (s) can be expressed as

W(s)=A

(s −z

)(s −z

)...(s−z

)

(s −p

)(s −p

)...(s−p

)

. (6.10)

The roots s = z

...are the zeros of W(s) and s = p

, p

...are the poles of W(s).

In general, z

and p

are complex numbers, and some of the roots may be repeated.

In the Laplace domain, the transfer function of a linear signal processing device can

therefore be fully described by its poles, its zeros, and a constant gain factor A.

A unit input signal I(s)=1 will result in the output signal V(s)=W (s).Re-

turning to the time domain we have L

−1

[1]=

(t) and L

−1

[W(s)] = w(t).The

inverse Laplace transform of the transfer function is thus the output signal for a unit

delta input signal, which we call the delta response of the system. Since, according

to Eq. (6.4b), a multiplication in the Laplace domain corresponds to a convolution

in the time domain, in the latter Eq. (6.6) reads as

v(t)=



∞

−∞

w(t −t



)i(t



)dt



. (6.11)

If w(t) and i(t) are causal, meaning that w(t)=i(t)=0fort < 0, the convolution

integral reads as

v(t)=



w(t −t



)i(t



)dt



. (6.12)

The transfer function W(s) and the delta response w(t) are two equivalent ways of

describing a linear system, and this is symbolized in Fig. 6.3. Using partial fraction

expansion, we can write the transfer function W (s) in Eq. (6.10) with m ≥ n as a

sum of terms with the form 1/(s − p

)

, where k

≥ 0 are integers and the poles

are complex numbers (p

= a

+ ib

). The delta response w(t) of a linear system

therefore becomes a sum of terms with the form

−1



(s −p

)



−1

−1)!

[cos(b

t)+isin(b

t)]

(t) k

≥ 1. (6.13)