Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

Solution Let ε . 0. We must ﬁnd a δ . 0 such that 0 , jx 2 4j, δ implies

jf ðxÞ2 14j, ε. As is usually the case, we work backward to ﬁnd a δ that

corresponds to the given ε. First, notice that there is a direct relationship between

jx 2 4j and jf ðxÞ2 14j:

jf ðxÞ2 14j5 j3x 1 2 2 14j5 j3x 2 12j5 3jx 2 4j:

From

this, we see that jf ðxÞ2 14j, ε if jx 2 4j, ε=3: Therefore δ 5 ε=3 is the value

for δ that we want. That is, if 0 , jx 2 4j, δ 5 ε=3; then jf ðxÞ2 14j, ε:

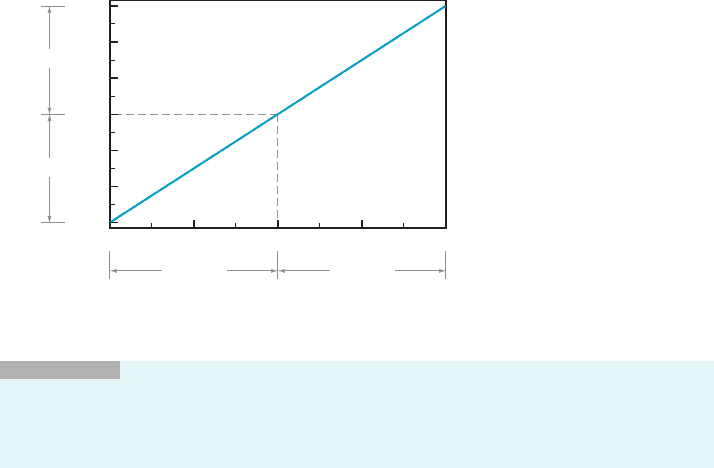
Compare Example 1 with Example 5 of Section 2.1. Both examples involve the

same func tion f, the same point c, and the same limit ‘. In the preceding section, we

speciﬁed a particular numerical value for ε, and then determined a corresponding

numerical value for δ. In the present discussion, we start with a general value of ε.Here

is how we ue the information from Example 1 in a numerical way. Suppose we want to

force f ðxÞ5 3x 1 2tobewithin0.06of14.Wesetε 5 0.06. The calculation in t he

example tells us that δ 5 ε=3 5 0:02: In short, if x is within δ 5 0 :02 of c 5 4, then

f ðxÞ5 3x 1 2isforcedtowithinε 5 0.06 of ‘ 5 14 (see Figure 2). Now suppose instead

that we want to force f ðxÞ to be within 0.003 of 14. To do this, we simply set ε 5 0.003.

Our computation tells us that when x is within of δ 5 ε=3 5 0:001 of c 5 4, then

f ðxÞ5 3x 1 2isforcedtowithinε 5 0.

003 of ‘ 5 14. When reﬁning our degree of

accuracy, we do not have to keep repeating the calculation. We have done the cal-

culation once and for all but with symbols ε and δ instead of speciﬁc numbers. We can

substitute numbers later, depending on the degree of accuracy desired.

INSIGHT

In Example 1, our intuition allows us to easily determine the required

limit. Why, then, has the ε-δ deﬁnition been introduced? The answer is that there are

many limits that are not obvious. (See, for example, the trigonometric limits at the end of

this section.) Having a rigorous deﬁnition allows us to verify limits in such situations.

One-Sided Limits Many useful functions that do not have limits at certain points do have one-sided

limits at those points. Furthermore, many functions are deﬁned on an interval

of the form ða; bÞ; ½a; b; ða; b ; ½a; bÞ or on a half line of the form ða; NÞ;

½a; NÞ; ð2N; bÞ; ð2N; b: The concept of one-sided limit is necessary to investigate

the behavior of such a function at an endpoint of its domain of deﬁnition.

3.980

14.06

13.94

13.96

14.04

14.02

14.00

13.98

3.990 4.000 4.010 4.020

d  0.02 d  0.02

e  0.06

m Figure 2

2.2 Limit Theorems 95

DEFINITION

Suppose that f is a funct ion deﬁned in an inte rval just to the right

of c. If, for every ε . 0, there is a δ . 0 such that jf ðxÞ2 ‘

j, ε for each x that

satisﬁes c , x , c 1 δ, then we say that f has ‘

as a limit from the right, or f has

right limit ‘

at c, and we write

lim

x-c

f ðxÞ5 ‘

Figure 3 shows a function f with a right limit ‘

at c.

DEFINITION

Let f be a function deﬁned in an interval just to the left of c. If, for

every ε . 0, there is a δ . 0 such that jf ðxÞ2 ‘

j, ε for each x that satisﬁes

c 2 δ , x , c, then we say that f has ‘

as a limit from the left, or f has left limit

‘

at c, and we write

lim

x-c

f ðxÞ5 ‘

Figure 4 illustrates a function f with left limit ‘

at c.

By comparing the deﬁnitions of one-sided and two-sided limits, we see that

lim

x-c

f ðxÞ5 ‘ is equivalent to



lim

x-c

f ðxÞ5 ‘ and lim

x-c

f ðxÞ5 ‘



⁄ EX

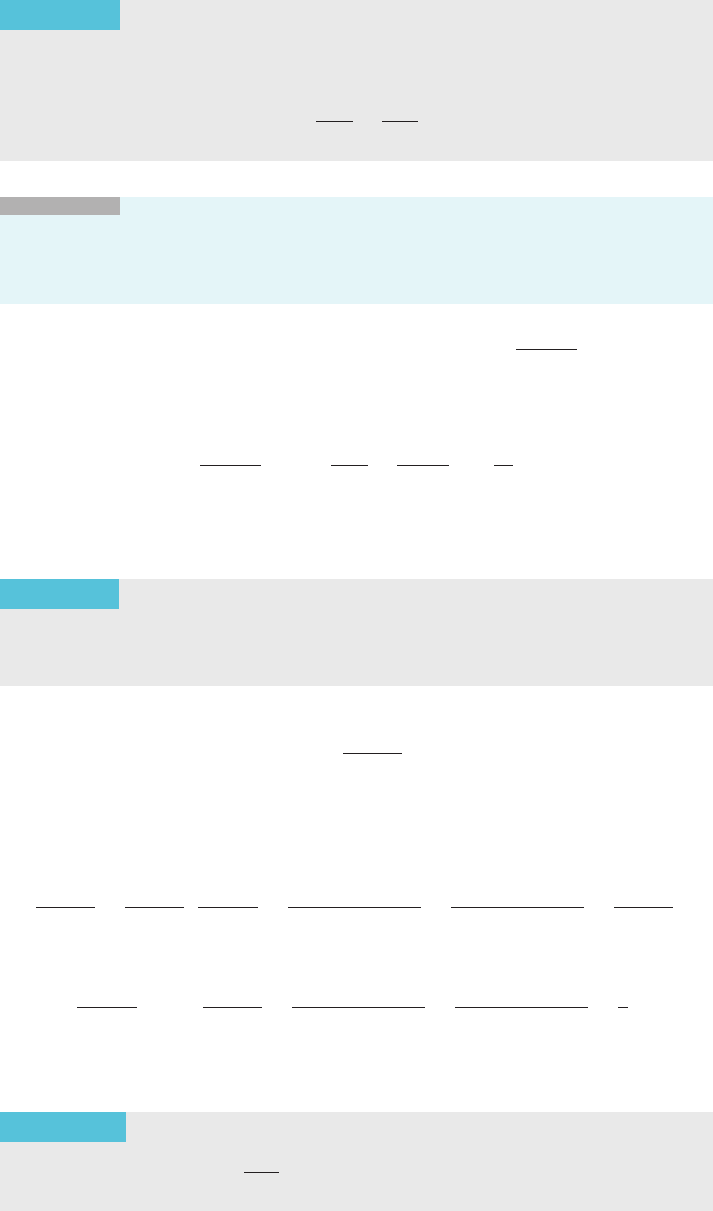
AMPLE 2 Determine the one-sided limits of f (x)at7iff is deﬁned by

f ðxÞ5

4x if x , 7

0ifx 5 7:

2 6ifx . 7

Solution As

with all limit problems, we ﬁrst look at this one intuitively. To the

right of c 5 7, f (x) is equal to 6 for every x, so it appears that f (x) has right limit

‘

526atc 5 7. To the left of c 5 7, f (x) is equal to 4x, so it appears that f (x)has

left limit ‘

5 4 7, or ‘

5 28 at c 5 7. Now let us carefully verify these assertions by

using the deﬁnitions (see Figure 5).

First we consider the right limit. Let ε . 0.

We must ﬁnd a positive δ such that,

if x is to the right of 7 by an amount less than δ, then f ðxÞ is within ε of ‘

526.

Because f ðxÞ526 for every value of x greater than 7, we have jf ðxÞ2

ð26Þj5 j2 6 2 ð26Þj5 0 for x . 7. Therefore no matter what positive value we

choose for δ, the inequality jf ð x Þ2 ð26Þj, ε holds for 7 , x , 7 1 δ. We may select

δ 5 1, for example, but any other choice of positive number for δ would do just as

well. By ﬁnding an appropriate δ for a given positive ε, we have shown that

lim

x-7

f ðxÞ526:

We now consider the left limit. Let ε . 0. We must ﬁnd a positive δ such that, if x is to

the left of 7 by an amount less than δ,thenf ðxÞ is within ε of ‘

5 28, or jf ðxÞ2 28j, ε:

Because f ðxÞ5 4x when x is to the left of 7, the desired inequality is j4x 2 28j, ε; or, on

multiplying each side of the inequality by 1/4, jx 2 7j, ε=4 : We therefore choose

δ 5 ε=4 and retrace our steps. Thus if jx 2 7j, δ, then we have 4jx 2 7j, 4δ,or

j4x 2 28j, ε,orjf ðxÞ2 ‘

j, ε: By deﬁnition, then, lim

x-7

f ðxÞ5 28. Notice in this

example that the ordinary (two-sided) limit, lim

x-7

f ðxÞ, does not exist. ¥

c ← x

y  f (x)

ᐉ

m Figure 3 lim

x-c

f ðxÞ5 ‘

x → c

y  f (x)

ᐉ

m Figure 4 lim

x-c

f ðxÞ5 ‘

98675

(7, 28)

(7, 5)

(7, 6)

4

m Figure 5

f ðxÞ5

4x if x , 7

fx 5 7

2 6ifx . 7

96 Chapter 2 Limits

Basic Limit Theorems There are a few simple theorems that save a great deal of work in calculating limits.

The ﬁrst tells us that a function can have at most one limit at a point c.

THEOREM 1

Suppose a function f is deﬁned on an open inte rval (a, c) to the

left of c and on an open interval (c, b) to the right of c. Then f cannot have two

distinct limits at c .

Theorem 1 will come up often, at least implicitly, as we study calculus. It

assures us that if we compute a limit by two different methods, then both methods

will give the same answer. A proof of Theorem 1 is outlined in Exercise 77.

Now we turn our attention to various arithmetic properties of limits. For

example, suppose that lim

x-c

f ðxÞ5 ‘: and lim

x-c

gðxÞ5 m. Given ε . 0, we can

take x close enough to c to ensure that f ðxÞ is within ε=2of‘ and gðxÞ is within ε=2

of m. Using the Triangle Inequality, we see that ðf 1 gÞðxÞ is within ε of ‘ 1 m for

these values of x:



f ðxÞ1 gð x Þ



2 ð‘ 1 mÞj 5 j



f ðxÞ2 ‘





gðxÞ2 m



# jf ðxÞ2 ‘j1 jgðxÞ2 mj Triangle

Inequality

5 ε:

This tells us that the limit of the sum f ðxÞ1 gðxÞ as x approaches c is the sum of the

limits of f ðxÞ and gðxÞ at c. We state this result, as well as some similar assertions, in

the following theorem, which tells us that limits of algebraic combinations of

functions behave in the expected way.

THEOREM 2

If f and g are two functions, c is a real number, and lim

x-c

f ðxÞ

and lim

x-c

gðxÞ exist, then the following equations hold

a. lim

x-c

ðf 1 gÞðxÞ5 lim

x-c

f ðxÞ1 lim

x-c

gðxÞ

lim

x-c

ðf 2 gÞðxÞ5 lim

x-c

f ðxÞ2 lim

x-c

gðxÞ;

b. lim

x-c

ðf  gÞðxÞ5



lim

x-c

f ðxÞ







lim

x-c

gðx



;

c. lim

x-c





ðxÞ5

lim

x-c

f ðxÞ

lim

x-c

gðxÞ

; provided that lim

x-c

gðxÞ 6¼ 0; and

d. lim

x-c



α  f ðxÞ



5 α 



lim

x-c

f ðxÞ



for any constant α.

By successively applying Theorem 2a as many times as necessary, we can

handle the sum of any ﬁnite number of functions. A similar remark applies to

Theorem 2b and any ﬁnite product of functions. For example, because we know

that lim

x-c

x 5 c, we can deduce that lim

x-c

5 c

for any positive integer n.

From these observations and the other parts of Theorem 2, we obtain the next

theorem.

2.2 Limit Theorems 97

THEOREM 3

If pðxÞ and qðxÞ are polynomials with qðcÞ 6¼ 0, then

lim

x-c

pðxÞ5 p ðcÞ

and

lim

x-c

pðxÞ

qðxÞ

pðcÞ

qðcÞ

INSIGHT

Functions of the form x/pðxÞ=qðxÞ where pðxÞ and qðxÞ are polynomials

are called rational functions. Theorem 3 gives a large class of functions (the rational

functions) with limits that can be obtained by evaluation. Later in this section, we will see

other important functions that have this convenient property.

⁄ EXAMPLE 3 Use Theorem 3 to compute lim

x-23

1 1

6x 2 5

Solution Let pðxÞ5 2x

1 1andqðxÞ5 6x2 5. Notice that qð23Þ 5 6ð23Þ2 5 5223.

Because this quantity is nonzero, it follows from Theorem 3 that

lim

x-23

1 1

6x 2 5

5 lim

x-23

pðxÞ

qðxÞ

pð23Þ

qð23Þ

: ¥

Notice that Theorems 2 and 3 allow us to calculate

limits without reference to the

ε-δ deﬁnition. Our next theorem can be used in the same way.

THEOREM 4

Let n be a positive integer and c a real number (that is positive if

n is even). Then

lim

x-c

ﬃﬃﬃ

ﬃﬃﬃﬃ

⁄ EX

AMPLE 4 Calculate

lim

x-9

ﬃﬃﬃ

2 3

x 2 9

Solution Because

the limit of the denominator is 0, Theorem 2c cannot be applied

to calculate the limit of the quotient. We must ﬁrst prepare the quotient by means

of an algebraic manipulation that is frequently helpful:

ﬃﬃﬃ

2 3

x 2 9

ﬃﬃﬃ

1 3

ﬃﬃﬃ

1 3



ﬃﬃﬃ

2 3

x 2 9

ﬃﬃﬃ

2 ð3Þ

ﬃﬃﬃ

1 3Þðx 2 9Þ

x 2 9

ﬃﬃﬃ

1 3Þðx 2 9Þ

ﬃﬃﬃ

1 3

Therefore using Theorems 2c, 2a, and 4 in succession, we have

lim

x-9

ﬃﬃﬃ

2 3

x 2 9

5 lim

x-9

ﬃﬃﬃ

1 3

lim

x-9

ﬃﬃﬃ

1 3Þ

ðlim

x-9

ﬃﬃﬃ

Þ1 3

: ¥

A Rule That Tells When

a Limit Does Not Exist

Sometimes it is useful to know a rule that shows that a certain limit does not exist.

THEOREM 5

If lim

x-c

gðxÞ5 0; and if f ðxÞ does not have limit 0 as x

approaches c, then lim

x-c

f ðxÞ

gðxÞ

does not exist.

98 Chapter 2 Limits

Proof. Let hðxÞ5 f ðxÞ=gðxÞ. To show that hðxÞ does not have a limit as x

approaches c, we write f ðxÞ5 gðxÞhðxÞ and argue by contradiction. If h(x) did

have a limit ‘ as x approached c, then Theorem 2b would give

lim

x-c

f ðxÞ5 lim

x-c

hðxÞlim

x-c

gðxÞ5 ‘  0 5 0;

contradicting the hypothesis about f. ’

INSIGHT

Here is an equivalent formulation of Theorem 5 that is frequently useful:

If lim

x-c

f ðxÞ

gðxÞ

exists, and if lim

x-c

gðxÞ5 0, then lim

x-c

f ðxÞ5 0:

⁄ EXAMPLE 5 Does lim

x-21

2 1 x

ð11xÞ

exist?

Solution We

notice that

lim

x- 2 1

ð2 1 xÞ5 2 1 ð21Þ5 1 6¼ 0 and lim

x- 21

ðx 1 1Þ



ð21Þ1 1



5 0

5 0:

According to Theorem 5, lim

x-21

ð2 1 xÞ

ð11xÞ

does not exist. ¥

The Pinching Theorem

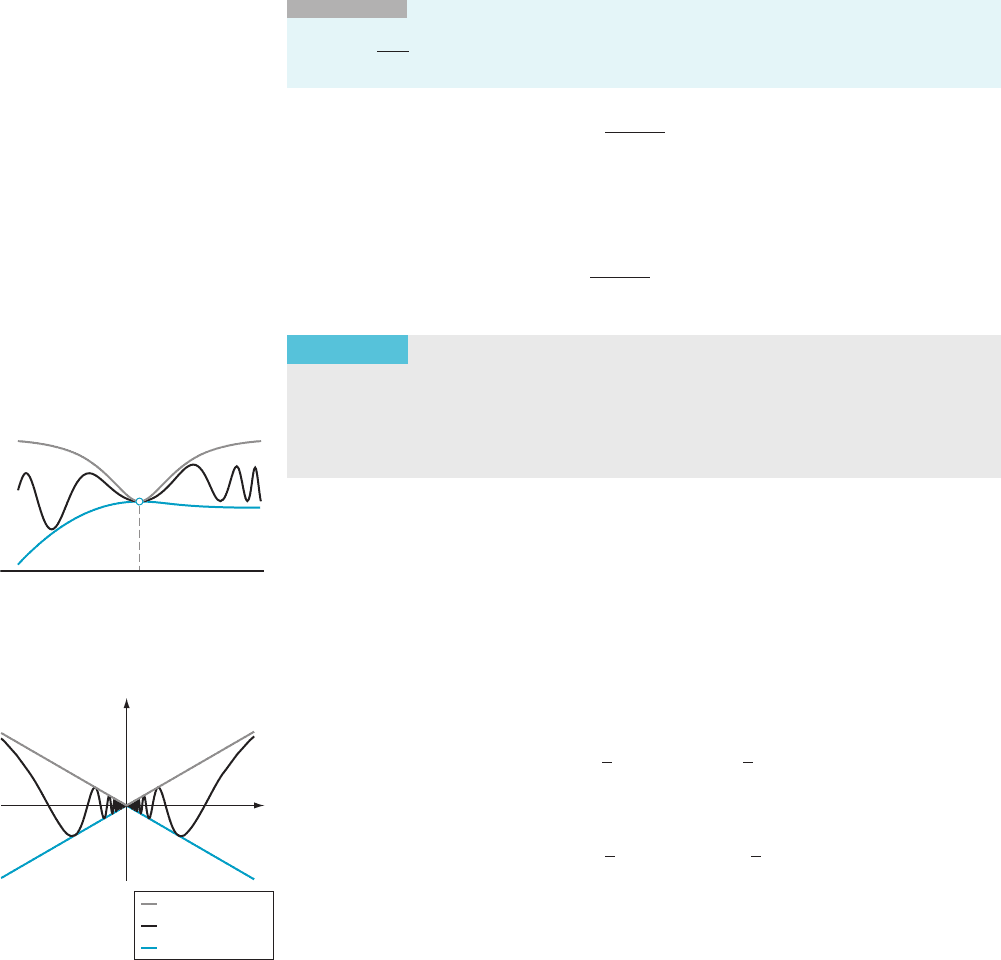
THEOREM 6

(The Pinching Theorem). Suppose that the functions f, g,andh

are deﬁned on an open interval (a, c) to the left of c andonanopeninterval(c, b)

to the right of c.LetS denote the union of these two intervals. Assume further

that gðxÞ # f ðxÞ # hðxÞ for all x in S (see Figure 6). If lim

x-c

gðxÞ5 ‘; and

lim

x-c

hðxÞ5 ‘, then lim

x-c

f ðxÞ5 ‘:

The truth of the Pinching Theorem is geometrically clear (refer to Figure 6).

We may apply the Pinching Theorem to one-sided limits as well. For example, if

gðxÞ # f ðxÞ # hðxÞ for all x in ðc; bÞ, if lim

x-c

gðxÞ5 ‘, and if lim

x-c

hðxÞ5 ‘,

then we may conclude that lim

x-c

f ðxÞ5 ‘.

⁄ EX

AMPLE 6 Let f ðxÞ5 x  sinð1=xÞ when x 6¼ 0. Use the Pinching Theo-

rem to compute lim

x-0

f ðxÞ.

Solution Notice

that, because



sinð1=xÞ



# 1 for every nonzero x, we have

f ðxÞ #



x  sin







5 jxj



sin







# jxj

and

2jxj #2jxj



sin







x  sin







# f ðxÞ:

In short,

2jxj # f ðxÞ # jxj: ð2:2:1Þ

We have “pinched” f (x) between hðxÞ5 jxj and gðxÞ52jxj (see Figure 7). Now it

is easy to see that

lim

x-0

jxj5 0 and lim

x-0

ð2jxjÞ5 0: ð2:2:2Þ

h(x)

(c, ᐉ)

f(x)

g(x)

m Figure 6 lim

x-c

f ðxÞ5 ‘

h(x)  x 

f(x)  xⴢ sin(1x)

g(x)  x 

m Figure 7

2.2 Limit Theorems 99

Equations (2.2.1) and (2.2.2), together with the Pinching Theorem, allow us to see

that lim

x-0

x  sinð1=xÞ5 0: ¥

Some Important

Trigonometric Limits

THEOREM 7

For every c, we have lim

t-c

sinðtÞ5 sinðcÞ and lim

t-c

cosðtÞ5

cos ðcÞ:

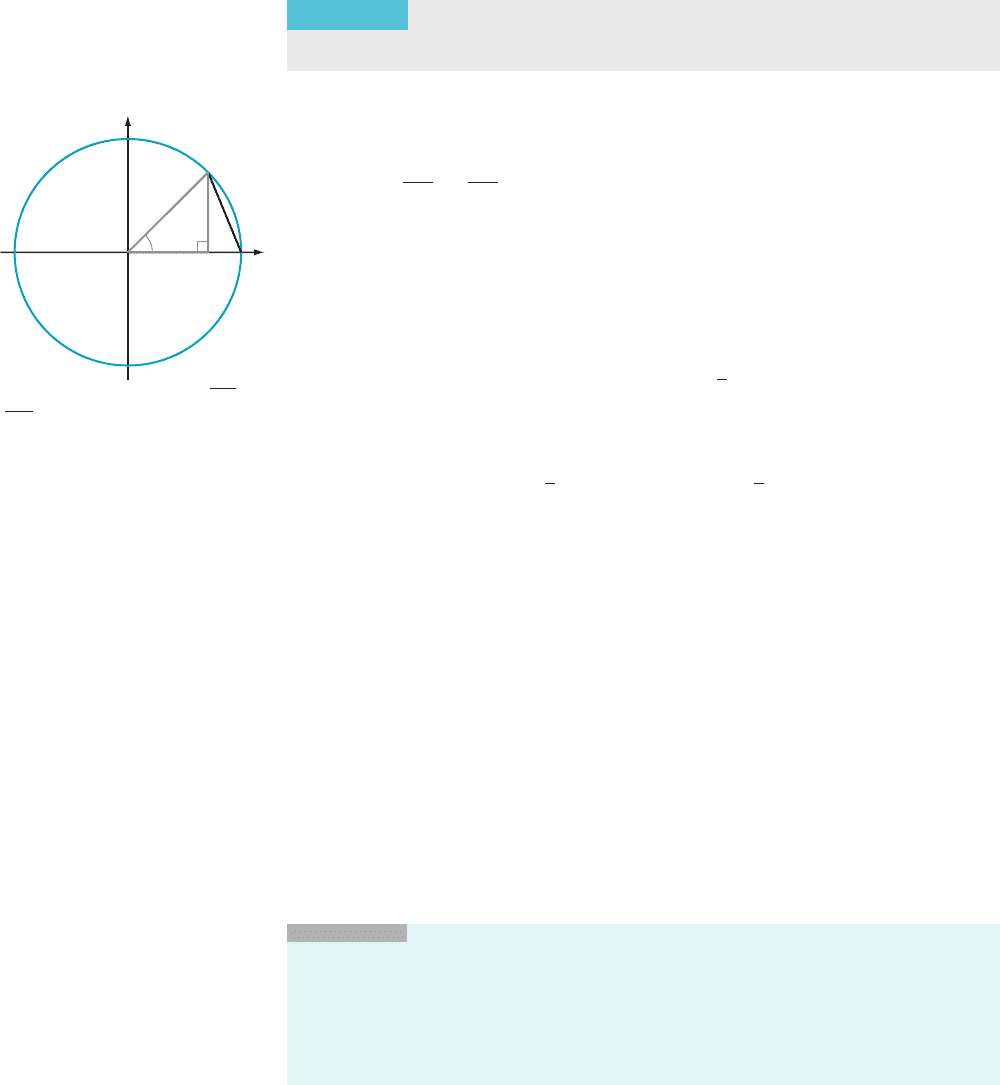
Proof. Let t be

an angle, measured in radians, between 0 and π/2. Figure 8

exhibits the unit circle. Because t represents a small positive angle measured in

radians, the length of the arc that the angle subtends is t. We see that

0 # sinðtÞ5 j

ABj, jACj, t : A similar picture shows that t , sinðtÞ # 0 when t is

negative. Therefore 2jtj, sinðtÞ, jtj for all t in ð2π=2; π=2Þ. By the Pinching

Theorem,

lim

t-0

sinðtÞ5 0: ð2:2:3Þ

Replacing θ with t in Half Angle Formula (1.6.12) and solving for cos (t), we obtain

cosðtÞ5 1 2 2 sin





It follows that

lim

t-0

cosðtÞ5 lim

t-0



1 2 2 sin





5 1 2 2 lim

t-0



sin





5 1 2 2  0

5 1: ð2:2:4Þ

Now let c be arbitrary. For every t, let h 5 t 2 c. Notice that h- 0ast- c.Wehave

lim

t-c

sinðtÞ 5 lim

t-c

sinðc 1 ðt 2 cÞÞ

5 lim

h-0

sinðc 1 hÞ Definition of h

5 lim

h-0

ðsinðcÞcosðhÞ1 cosðcÞ sinðhÞÞ Addition Formula ð1:8Þ

5 lim

h-0

ðsinðcÞcosðhÞÞ1 lim

h-0

ðcosðcÞsin ðhÞÞ Theorem 2a

5 sinðcÞlim

h-0

cosðhÞ1 cosðcÞlim

h-0

sinðhÞ Theorem 2d

5 sinðcÞ1 1 cosðcÞ0 Equations ð2:2:3Þ and ð2:2:4Þ

5 sinðcÞ

A similar calculation using Addition Formula (1.9) shows that lim

t-c

cosðtÞ5

cosðcÞ for every real c. ’

INSIGHT

Because cscðxÞ5 1=sinðxÞ, secðxÞ5 1=cosðxÞ, tanðxÞ5 sinðxÞ=cosðxÞ, and

cotðxÞ5 cosðxÞ =sin ðxÞ, we may use Theorem 2c to conclude that, if f is any trigonometric

function, then

lim

x-c

f ðxÞ5 f ðcÞ

at each point c in the domain of f.

sin(t)

m Figure 8 0 # sinðtÞ5 jABj,

ACj, t

100 Chapter 2 Limits

We now have a large class of functions with limits that can be computed simply

by evaluation: polynom ials, rational functions, n

roots, trigonometric functions,

and all the combinations thereof that can be formed with the arithmetic operations

described in Theorem 2. However, many limits in calculus are not obtained so

easily. The next theorem gives two important examples.

THEOREM 8

If t is measured in radians, then

lim

t-0

sinðtÞ

5 1 and lim

t-0

1 2 cosðtÞ

: ð2:2:5Þ

Proof. Let f (t) 5 sin

(t)/t, t 6¼0. On a calculator we compute that

t 0

.1 0.01 0.001 0.0001

f (t) 0.9983341664 0.9999833334 0.9999998333 0.9999999983

to ten decimal places. On the basis of this numerical evidence, it is reasonable to

guess that lim

t-0

f ðtÞ5 1: Let us inves tigate why.

Refer again to Figure 8. As we observed in the course of proving Theorem 7,

Figure 8 shows that sinðt Þ, t or, equivalently,

f ðtÞ, 1: ð2:2:6Þ

This pinches f (t ) from above by the constant function h(t) 5 1. Now we will pinch

f (t) from below. See Figure 9, which is similar to the preceding ﬁgure except chord

AC of Figure 8 has been replaced with tangent line segment

AD. Because +OAD

is a right angle, we see that ΔABD is similar to ΔOBA. It follows that

jBDj

ADj

sinðtÞ

Therefore j

BCj, jBDj5 jADjsinðtÞ: However, we see from Δ OAC that

ADj5 tanðtÞ. It follows that

BCj, tan ðtÞsinðtÞ:

Therefore

BCj1 sinðtÞ, tanðtÞsinðtÞ1 sinðtÞ5 sinðtÞð1 1 tanðtÞÞ: ð2:2:7Þ

Now observe that t , j

BCj1 sinðtÞ (see Figure 10). This inequality, together with

inequality (2.2.7), shows that

t , sinðtÞð1 1 tan ðtÞÞ:

Divide each side of this inequality by the positive quantity tð1 1 tanðtÞÞ to obtain

1 1 tanðtÞ

sinðtÞ

5 f ðtÞ:

sin(t)

m Figure 9 t 5 ﬀAOD 5

ﬀBAD 5

2 ﬀADO

sin(t) sin(t)

AB

BC

m Figure 10

2.2 Limit Theorems 101

Thus for small positive t, we have pinched f (t) from below by gðtÞ5 1= ð1 1 tanðtÞÞ.

Because lim

t-0

1=ð1 1 tan ðtÞÞ5 1=ð1 1 tanð0ÞÞ5 1, the Pinching Theorem tells us

that we have lim

t-0

f ðtÞ5 1. But f ð2 tÞ5 f ðtÞ. It follows that lim

t-0

f ðtÞ5

lim

t-0

f ðtÞ5 1. We conclude that the two-sided limit of f ðtÞ at t 5 0 exists and

equals 1, which is the ﬁrst limit formula of Theorem 8.

For the second limit formu la, we use the Half Angle Formula

1 2 cosðtÞ5 2 sin

ðt=2Þ to obtain

1 2 cosðtÞ

2 sin

ðt=2Þ



sinðt=2Þ

t = 2



: ð2:28Þ

Let x 5 t=2 and observe that x-0ast-0. Using equation (2.2.8) and the limit

formula for sin ðxÞ=x that we established in the ﬁrst part of this proof, we conclude

that

lim

t-0

1 2 cosðtÞ

5 lim

t-0



sinðt=2Þ

t=2



5 lim

x-0



sinðxÞ



lim

x-0



sinðxÞ





lim

x-0

sinðxÞ



 1

: ’

⁄ EX

AMPLE 7 Show that

lim

t-0

1 2 cosðtÞ

5 0:

Solution By

Theorem 8 and Theorem 2b, we have

lim

t-0

1 2 cosðtÞ

5 lim

t-0

1 2 cosðtÞ

 t 5 lim

t-0

1 2 cosðtÞ

 lim

t-0

t 5

 0 5 0: ¥

QUICK QUIZ

1. True or false: The limit lim

x-c

f ðxÞ may exist even if c is not in the domain of f.

2. True or false: If lim

x-c

f ðxÞ5 ‘ and c is in the domain of f, then ‘ 5 f ðcÞ.

3. True or false: If f has both a left limit and a right limit at c, then lim

x-c

f ðxÞ

exists.

4. Evaluate lim

x-0

sinðxÞ

Answers

1. True 2. False 3. False 4. 1

EXERCISES

Problems for Practice

c In Exercises 128, evaluate the given limit. b

1. lim

x-3

2. lim

x-1

ð6x 2 1Þ

3. lim

x-6

ðx=3 1 2Þ

4. lim

x-12

ð3 2 x=4Þ

5. lim

x-0

ﬃﬃﬃ

2 πxÞ

6. lim

x-3

2 4x 1 3

x 2 3

7. lim

x-22

2 4

x 2 2

8. lim

x-2

2 4

x 2 2

102 Chapter 2 Limits

c In Exercises 9212, the indicated limit lim

x-c

f ðxÞ does not

exist. Prove it by evaluating the one-sided limits lim

x-c

f ðxÞ

and lim

x-c

f ðxÞ. b

9. lim

x-25

f ðxÞ where

f ðxÞ5

3x if x , 5

4ifx . 5



10. lim

x-23

f ðxÞ where

f ðxÞ5

if x ,23

4x if x .23



11. lim

x-1

f ðxÞ where

f ðxÞ5

0ifx , 1

2 4ifx . 1



12. lim

x-0

f ðxÞ where

f ðxÞ5

x 2 1ifx , 0

if x $ 0



c In Exercises 13216,showthatlim

x-4

f ðxÞ exists by calcu-

lating the one-sided limits lim

x-4

f ðxÞ and lim

x-4

f ðxÞ. b

13. f ðxÞ5

1 1ifx , 4

5x 2 3ifx . 4



14. f ðxÞ5

2x 1 3ifx , 4

x 1 7ifx . 4



15. f ðxÞ5

if x , 4

2 64 if x 5 4

if x . 4

16. f ðxÞ5

8ifx , 4

5ifx 5 4

2x if x . 4

c In Exercises 17224, use Theorem 2 to evaluate the

limit. b

17. lim

x-4

ð2x 1 6Þ

18. lim

x-23

ð24x 1 5Þ

19. lim

x-1

ðx

2 6Þ

20. lim

x-2

ðx 1 1Þ=x

21. lim

x-0

ðx

1 2Þ=ðx 1 1Þ

22. lim

x-7

ðx 1 3Þðx 2 7Þ

23. lim

x-4

ðx 2 5Þx

x 1 1

24. lim

x-22

ðx

11Þ

c In each of Exercises 25232, either determine that the limit

does not exist or state its value. Justify your answer using

Theorems 3, 4, and 5. b

25. lim

x-1

ðx22Þ

x 1 1

26. lim

x-4

x 1 4

x 2 4

27. lim

x-3

2 9

x 2 3

28. lim

x-22

2 4

x 2 2

29. lim

x-21

2 1

x 1 1

30. lim

x-16

ﬃﬃﬃ

1=ðx

1=4

2 10Þ

31. lim

x-π

x 2

ﬃﬃﬃ

2 3

32. lim

x-π

2 9

ðx2πÞ

c Use the Pinching Theorem to evaluate the limits in

Exercises 33238. b

33. lim

x-0

cosð1=xÞ

34. lim

x-1

ðx 2 1Þsinð1=ðx 2 1ÞÞ

35. lim

x-5



1 1 ðx25Þ

sinðcsc ðπxÞÞ



36. lim

x-29



4 1 ðx 1 9Þ cos



1=ð9 1 xÞ





37. lim

x-2



ðx 1 1Þ1 ð x22Þ

sinðsec ðπ=xÞÞ



38. lim

x-0



cosð1 1 xÞ1 x

1=3

cosð1=xÞ



c In Exercises 39242, decide whether the limit can be

determined

from the given information. If the answer is yes,

then ﬁnd the limit. b

39. 2 2 jx 2 2j

# f ðxÞ # 2 1 jx 2 2j

; lim

x-2

f ðxÞ

40. 2 2 jx 2 2j

# f ðxÞ # 2 1 jx 2 2j

; lim

x-4

f ðxÞ

41. 23jxj1 5jx 2 5j # f ðxÞ # 6jxj1 ðx25Þ

; lim

x-0

f ðxÞ

42. 20 2 jx 2 2j # f ðxÞ # x

2 4x 1 24; lim

x-2

f ðxÞ

c In Exercises 43246, investigate the one-sided limits of the

function

at the endpoints of its domain of deﬁnition. b

43. f ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ﬃ

ðx 2 1Þð2 2 xÞ

44. f ðxÞ5

x 2 1

2 1

; 21 , x , 1

45. f ðxÞ5

2 4

1 2x

; 22 , x , 2; x 6¼ 0

46. f ðxÞ5

ﬃﬃﬃ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 x

; 0 , x , 1

Further Theory and Practice

c In Exercises 47256, use your intuition to decide whether

the limit exists. Justify your answer by using the rigorous

deﬁnition of limit. b

47. lim

x-24

jxj=x

48. lim

x-0

jxj=x

49. lim

x-27

ðjxj2 3xÞ

50. lim

x-1

2 1

jx 2 1j

2.2 Limit Theorems 103

51. lim

x-23

ðx 2 jxjÞ

52. lim

x-23

f ðxÞ where

f ðxÞ5

6ifx #23

22x if x .23



53. lim

x-3

f ðxÞ where

f ðxÞ5

if x # 0

1 2 x

if x . 0



54. lim

x-4

f ðxÞ where

f ðxÞ5

2 1ifx , 4

3x 1 3ifx $ 4



55. lim

x-5

f ðxÞ where

f ðxÞ5

x 1 1ifx , 5

x 2 1ifx $ 5



56. lim

x-2

f ðxÞ where

f ðxÞ5

1 x 2 6

x 2 2

if x , 2

2 2x

1 x 2 2

x 2 2

if x . 2

c In Exercises 57266, use the basic limits of Theorem 8 to

evaluate

the limit. Note: x



means “x degrees.” b

57. lim

x-0

sinð3xÞ

58. lim

x-0

tanð2xÞ

59. lim

x-0

sinð2xÞ

sinðxÞ

60. lim

x-0

sin

ðxÞ

1 2 cosðxÞ

61. lim

x-0

1 2 cosðxÞ

tanðxÞ

62. lim

x-0

sinðxÞ2 tanðxÞ

63. lim

x-0

sinðx



64. lim

x-0

1 2 cosðx



65. lim

x-0

sinð2xÞtanð3xÞ

66. lim

x-0

sin

ð3x

c In Exercises 67 273, use algebraic manipulation (as in

Example 5) to evaluate the limit. b

67. lim

x-1



2 1

ﬃﬃﬃ

2 1



68. lim

x-4



x 2 4

ﬃﬃﬃ

2 2



69. lim

h-0

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 2h

2 1

70. lim

t-0



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

3 1 t

ﬃﬃﬃ



71. lim

h-0



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

4 1 h



72. lim

x-4

 ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

8 2 x 2 2

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

5 2 x 2 1



73. lim

x-4

ﬃﬃﬃ

2 2

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

x 1 5

2 3

c In Exercises 74280, evaluate the one-sided limits. b

74. lim

x-3

x 2 3

jx 2 3j

75. lim

x-3

x 2 3

jx 2 3j

76. lim

x-3



6 1 x

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

13 2 2x



77. lim

x-4

x 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

16 2 3x

x 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

16 2 x

78. lim

x-0

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

sinðxÞ

ﬃﬃﬃ

79. lim

x-0

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

sinðxÞ

ﬃﬃﬃ

80. lim

x-1

ﬃﬃﬃ

2 1Þ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 3x 1 2

ð12xÞ

3=2

81. Suppose that ‘

and ‘

are two unequal numbers.

5 j‘

2 ‘

j=2: Notice that ε

. 0: Suppose that

lim

x-c

f ðxÞ5 ‘

. Then there is a δ

. 0 such that

jf ðxÞ2 ‘

j , ε

for all values of x satisfying

0 , jx 2 c j, δ

. Show that there is no δ

. 0 such that

jf ðxÞ2 ‘

j , ε

for all values of x satisfying

0 , jx 2 c j, δ

. Conclude that lim

x-c

f ðxÞ5 ‘

impossible.

82. Prove the following variant of Theorem 5: If

lim

x-c

f ðxÞ=gðxÞ exists, and lim

x-c

gðxÞ5 0, then

lim

x-c

f ðxÞ5 0.

c In Exercises 83286, use the Pinching Theorem to establish

the

required limit. b

83. If

0 # f ðxÞ # x

for all x, then lim

x-0

f ðxÞ=x 5 0:

84. If jgðxÞ2 f ðxÞj #

ﬃﬃﬃﬃﬃ

jxj

; and if lim

x-0

f ðxÞ5 ‘, then

lim

x-0

gðxÞ5 ‘.

85. If lim

x-c

jf ðxÞj5 0, then lim

x-c

f ðxÞ5 0:

86. If lim

x-c

f ðxÞ5 0; then lim

x-c

ðxÞ5 0:

104 Chapter 2 Limits