Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

7. lim

x-N

x 1 cosðxÞ

x 2 sinðxÞ

8. lim

x -1N

ﬃﬃﬃ

x 1 1

9. lim

x-1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

x 2 1

10. lim

x-01

cscðxÞ

11. lim

x -1N

2 4x 1 9

2 8x 1 18

12. lim

x-3

cosðxÞ

x 2 3

13. lim

x-0

csc

ðxÞ

14. lim

x-1N

1 5x 2 7

1 4

15. lim

x-0

ﬃﬃﬃﬃﬃ

jxj

16. lim

x -1N

ﬃﬃﬃ

2 5

ﬃﬃﬃ

1 4

17. lim

x-0

cotðxÞ

18. lim

x-2N

4=3

1 sinðxÞ

19. lim

x-2

tanðπ=xÞ

20. lim

x -1N

sinðxÞ

c In each of Exercises 21234, a function f is

given. Find all

horizontal and vertical asymptotes of the graph of y 5 f (x).

Plot several points and sketch the graph. b

21. f ðxÞ5

x 2 7

22. f ðxÞ5

2 1

2 4

23. f ðxÞ5

ﬃﬃﬃﬃﬃ

jxj

24. f ðxÞ5

ﬃﬃﬃﬃﬃ

jxj

x 1 3

25. f ðxÞ5

ðx21Þ

2=3

ðx

18Þ

1=3

26. f ðxÞ5

1 1

27. f ðxÞ5

1 1

28. f ðxÞ5

2 7x 1 12

29. f ðxÞ5

1=3

jxj

30. f ðxÞ5

ðx 1 1Þðx 1 4Þ

31. f ðxÞ5

ðx14Þ

21=3

x ðx 1 1Þ

32. f ðxÞ5

1 1

2 1

33. f ðxÞ5 cotðxÞ; 2

, x ,

34. f ðxÞ5 secðxÞ; 2

, x ,

Further Theory and Practice

35. Formulate and prove a version of Theorem 1 (the Limit

Uniqueness Theorem) from Section 2.2 for lim

x -1N

f ðxÞ

and lim

x-2N

f ðxÞ:

36. Formulate and prove a version of Theorem 2 (the sum,

difference, product, quotient, and scalar multiplication

rules for limits) from Section 2.2 for the limits

lim

x -1N

f ðxÞ and lim

x-2N

f ðxÞ:

37. Formulate and prove a version of the Pinching Theorem

from Section 2.2 for the limits lim

x -1N

f ðxÞ and

lim

x-2N

f ðxÞ:

38. We do not attempt to formulate sum, difference, product,

or quotient rules for inﬁnite valued limits (as in the ﬁrst

deﬁnition of “limit” in this section) because there are ser-

ious ambiguities in doing arithmetic with the symbols 1N

and 2N. Give examples to illustrate these ambiguities.

39. Prove that, if lim

x-c

F ðxÞ5 ‘ 2 R; and if

lim

x-c

GðxÞ51N, then lim

x-c



FðxÞ1 GðxÞ



51N:

Similarly, if lim

x-c

HðxÞ52N, then prove that

lim

x-c



FðxÞ1 HðxÞ



52N:

c In each of Exercises 40245, a function f is

given. Find all

horizontal and vertical asymptotes of the graph of y 5 f (x).

Plot several points, and sketch the graph. b

40. f ðxÞ5 sinðxÞ=x

41. f ðxÞ5 x=sinðxÞ

42. f ðxÞ5 jxj

1=2

=sinðxÞ

43. f ðxÞ5 cos

ðxÞ=x

44. f ðxÞ5 jxj=sinðxÞ

45. f ðxÞ5 1=jsinðxÞj

c In Exercises 46248, graph the function f.

Refer to the

deﬁnition of “vertical asymptote” to decide if x 5 0 is a ver-

tical asymptote of the graph of f. b

46. f ðxÞ5 sinð1=xÞ

47. f ðxÞ5 jsinð1=xÞ=xj

48. f ðxÞ5



1:1 1 sinð1=xÞ



49. Let fðxÞ5 x=10

100

and gðxÞ5 10

100

=x. What are f (10

)

and g(10

)? Now compute lim

x-N

f ðxÞ and lim

x-N

gðxÞ.

Is it signiﬁcant that f (x) is much smaller than g(x) for all

0 , x , 10

? (The number 10

was chosen simply

because it is large. It is on the order of the number of

protons in the universe.)

c Exercises 50252 concern physical laws that entail natural

one-sided

limits and vertical asymptotes. In each exercise,

sketch the graph and indicate the vertical asymptote. b

50. m 5 m

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 ðv=cÞ

(Einstein’s Relativistic Mass Law,

which relates the mass m of an object at velocity v to its

rest mass m

and to the speed of light c.)

51. P 5 RT=ðV 2 bÞ2 a=V

(This is Van der Waals’s equa-

tion relating the pressure P and volume V of 1 mole of

a gas at constant temperature T. The constant R is

2.4 Inﬁnite Limits and Asymptotes 125

the universal gas constant, and the constant a depends

on the particular gas under consideration. The constant b

is the volume occupied by the gas molecules themselves.)

52. H 5 2gR

=ð2gR 2 v

Þ2 R (This is the equation for the

height H a missile rises above Earth’s surface as a func-

tion of its initial velocity v

; g is the acceleration due to

Earth’s gravity, and R is Earth’s radius.)

53. If f is a continuous function on a closed interval [a, b]?,

can the graph of f have a vertical asymptote x 5 c where c

is a value in [a, b]? Explain your reasoning.

54. In an enzyme reaction, the reaction rate V is given in

terms of substrate amount S by

V 5

K 1 S

Identify V

as a limit as S-N. Although V does not have

a maximum value, V

is called the maximum velocity

(where velocity refers to reaction rate). Explain why.

c In Exercises 55258, you are asked to investigate the

notion

of a skew asymptote, which is also called a slant

asymptote and an oblique asymptote. b

55. We

say that the graph of a function f has the line

y 5 mx 1 b as its skew asymptote if either

lim

x -1N



f ðxÞ2 ðmx 1 bÞ



5 0

lim

x-2N



f ðxÞ2 ðmx 1 bÞ



5 0

a. If m 5 0, prove that this notion of skew asymptote

coincides with the notion of horizontal asymptote.

b. If f (x) 5 p(x)/q(x) is a quotient of polynomials

(a rational function), then prove that a necessary

condition for the graph of f to have mx 1 b as a skew

asymptote, with m 6¼0, is that the degree of p is pre-

cisely one greater than the degree of q.

c. If the degree of p exceeds the degree of q by precisely

two, then we could say that the graph of f is asymp-

totic to a parabola. Explain this idea in more detail,

and give a precise deﬁnition.

56. Find all horizontal, vertical, and skew asymptotes of the

graphs of the following functions. Then plot some points

and give a sketch.

a. f ðxÞ5

x 2 5

b. gðxÞ5

3=2

1=2

1 7

c. kðxÞ5

ðx

1 4x 1 3Þ

4=3

ðx 2 9Þ

5=3

d. mðxÞ5 ðx 1 5Þ

sinð1=xÞ

ð1=xÞ

57. Find all parabolic asymptotes for the functions

Fð xÞ5 x

=ðx 1 3Þ; GðxÞ5 x

=ðx

1 5xÞ, and HðxÞ5

ðx

7=3

1 x

1=3

Þ=ðx

1=3

1 1Þ. (Refer to Exercise 55, part c,

for terminology.) Sketch the graphs of H and its parabolic

asymptote.

58. Consider the following three attempts at determining the

skew asymptote of the function

f ðxÞ5

1 3x 1 2

x 2 1

Determine which argument is correct and explain what is

wrong with the others.

a. Because

f ðxÞ 5

1 3x 1 2

x 2 1

ð1 1 3=x 1 2=x

ð1 2 1=xÞ

5 x

ð1 1 3=x 1 2=x

ð1 2 1=xÞ

and because the fraction tends to 1 as x-N, the skew

asymptote must be x 1.

b. Because

f ðxÞ 5

1 3x 1 2

x 2 1

ðx 1 3 1 2=xÞ

ð1 2 1=xÞ

ðx 1 3 1 2=xÞ

ð1 2 1=xÞ

and because the numerator tends to x 1 3 and the

denominator to 1, the skew asymptote must be x 1 3.

c. Because

f ðxÞ5

1 3x 1 2

x 2 1

5 x 1 4 1

x 2 1

;

the skew asymptote must be x 1 4.

Calculator/Computer Exercises

c Sometimes the asymptotic behavior of a graph takes place

very slowly. In Exercises 59 and 60, you are asked to perform

numerical calculation to determine how slowly the limit is

being achieved. b

59. We know that

lim

x - 1N

ﬃﬃﬃ

x 1 1

5 0:

How large must x be to guarantee that the function is

smallert than 0.001?

60. We know that

lim

x-0 2

jxj

1=4

1 6

1=3

52N:

How close must x be to 0 to guarantee that

ðjxj

1=4

1 6Þ=x

1=3

,210

126 Chapter 2 Limits

c In Exercises 61263, the function f has one or more hor-

izontal asymptotes. Plot f and its horizontal asymptote(s).

Specify another window in which f and its right horizontal

asymptote appear to nearly coincide. Repeat for the left

horizontal asymptote if it is different. b

61. f ðxÞ5

1 x cosðxÞ

1 1

62. f ðxÞ5

1 sinðxÞ

jxj

1 1

63. f ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 x sinðxÞ

1 2x 1 2

c In Exercises 64266, the function f has

one or more vertical

asymptotes. Plot f and its vertical asymptote(s). b

64. f ðxÞ5

1 x 1 3

2 x 2 3

65. f ðxÞ5

4 1 cosðxÞ

sinðxÞ1 cosð2xÞ

; 0 # x # 3

66. f ðxÞ5

1 1

2 3x 1 1

2.5 Limits of Sequences

This section addresses limits of inﬁnite sequences of real numbers. Recall that an

inﬁnite sequence f of real numbers is a function with domain Z

and range R (as

discussed in Section 1.4). Following the common convention for sequences, we will

write f

instead of f ðnÞ and refer to the sequence as ff

n51

or just ff

g for short.

Our interest here is whether the numbers f

tend to some limit as n tends to inﬁnity.

Before giving a precise deﬁnition of “limit,” let’s apply our intuition to some

examples.

⁄ EX

AMPLE 1 We suppose that a quantity of radioactive material is

decaying. At the beginning of each week, there is half as much material as there

was at the beginning of the previous week. The initial quantity is 5 g. Use sequence

notation to express the amount of material at the beginning of the n

week. Does

this sequence have a limit?

Solution The

amount a

of material at the start of the ﬁrst week is 5 g. The amount

of material at the start of the second week is 5/2 g. The amount a

of material at

the start of the third week is 5/4 g. Similarly, the amounts at the beginnings of the

fourth and ﬁfth weeks are a

5 5=8 g and a

5 5=16 g. In general, the amount a

material at the start of the n

week is given by a

5 5 ð1=2Þ

n21

: The magnitude of

each term is half of its predecessor. Our intuitive conclusion is that the amount

of radioactive material tends to 0 as the number of weeks tends to inﬁnity.

INSIGHT

A sequence fa

n51

can be graphed in the same way as any other real-

valued function. We simply plot the points ð1; a

Þ, ð2; a

Þ, ð3; a

Þ, and so on. Figure 1

shows the points ð1; 5Þ, ð2; 5=2Þ, ð3; 5=4Þ, ð4; 5=8Þ, ð5; 5=16Þ, ð6; 5=32Þ, and ð7; 5=64Þ of the

sequence fa

n51

from Example 1. Each point is half the distance to the x-axis of the

preceding point. The graph conﬁrms our intuitive conclusion that a

tends to 0 as n tends

to inﬁnity.

7436521

 5ⴢ



n1

m Figure 1

2.5 Limits of Sequences 127

⁄ EXAMPLE 2 Set a

5 ð21Þ

. Does the sequence fa

j51

tend to a limit as j

tends to inﬁnity?.

Solution By

calculating a

5 ð21Þ

for j 5 1; 2; 3; 4;:::; we may write out this

sequence as 21; 1; 21; 1;::::The sequence does not seem to tend to any limit: Half

of the time the value is 1, and the other half, the value is 21. The sequence does

not become and remain close to a single value. Therefore we say that it has no limit

(see Figure 2).

INSIGHT

In Example 1, we used n as the index variable of a sequence, whereas in

Example 2, we used j. There is no signiﬁcance to the letter that is used because the

index variable merely serves as a placeholder for the integers 1, 2, 3, ....Theletters i, j, k,

m, and n are all commonly used as index variables of sequences.

A Precise Discussion

of Convergence and

Divergence

DEFINITION

Suppose fa

n51

is a sequence, and ‘ is a real number. We say the

sequence has limit ‘ (or converges to ‘) if, for each ε . 0, there is an integer N

such that ja

2 ‘j, ε for all n $ N (see Figure 3).

When the sequence f a

n51

has limit ‘, we write

lim

n-N

5 ‘;

-‘ as n-N:

A sequence that has a limit is said to be convergent. If a sequence does not converge, then

we say that it diverges, and we call it a divergent sequence.

INSIGHT

In Section 2.4, we discussed the limit at inﬁnity, lim

x-N

f ðxÞ, for a func-

tion f of a continuous real variable x. The deﬁnition of lim

n-N

is very similar. The

difference is that a

is deﬁned for only positive integer values of n.

⁄ EXAMPLE 3 Discuss convergence for the sequence 1, 1/2, 1/3, 1/4, . . . .

Solution Let a

5 1/n for all n. The term s a

get progressively closer to 0. Let us

now verify that lim

n-N

5 0. We set ‘ 5 0 and suppose that ε is a given positive

7436521

1

2

m Figure 2

ᐉ

ᐉ  e

ᐉ  e

m Figure 3 ja

2 ‘j, ε for n $ N

128 Chapter 2 Limits

number. We reason backward to select N. To guarantee that ja

2 ‘j, ε, we need.

j1=n  0j , ε: This simply means that 1=n , ε: This last inequality is satisﬁed if

n . 1=ε: Therefore we select N to be the ﬁrst integer that is greater than 1=ε.If

n $ N, then n . 1=ε is true. Therefore 1=n , ε and ja

2 ‘j, ε. In conclusion,

lim

n-N

5 0: ¥

The Tail of a Sequence Intuitively, we say that fa

n51

converges to ‘ if a

is as close as we please to ‘ when

n is large enough. A crucial feature of this idea is that convergence depends only on

what fa

n51

does when n is large. The values of the ﬁrst ten thousand (or ﬁrst

million, or ﬁrst billion, etc.) terms are irrelevant. If we ﬁx any N, then we refer to

the terms

N11

; a

N12

; a

N13

;:::

as the tail end (or simply the tail) of the sequence fa

g. Of course, since N is an

arbitrary positive integer, there are inﬁnitely many tail ends of a sequence.

⁄ EX

AMPLE 4 Find the limit of the sequence deﬁned by

0if1# n # 100000

10 if n $ 100001



Solution T

he sequence fa

n51

converges to 10. To see this, pick ε . 0: Let

N 5 100001. If n $ N; then a

5 10 and ja

 10j5 j10  10j5 0 , ε; as desired. ¥

Some Special

Sequences

A number of special sequences occur repeatedly in our work. We now collect

several of these sequences for easy reference. Some of these sequences diverge

because their terms grow without bound. It is convenient to extend the limit

notation to include these types of divergent sequences.

DEFINITION

If, for any M . 0; there is an N such that a

. M for all indices

n $ N; then we write

lim

n-N

5 N

and say that the sequence fa

g tends to inﬁnity. If for any M , 0; there is an N

such that a

, M for all indices n $ N, then we write

lim

n-N

52N

and say that the sequence fa

g tends to minus inﬁnity.

⁄ EX

AMPLE 5 Suppose that fa

g is a sequence of nonzero numbers such

that lim

n-N

5 N. Show that lim

n-N

5 0.

Solution It

is evident that, as the terms of a sequence get larger, their reciprocals

get smaller. It is not hard to verify this deduction using the precise deﬁnitions

that have been given. Given ε . 0; let M be an integer that satisﬁes M . 1=ε:

2.5 Limits of Sequences 129

By hypothesis, there is an integer N such that a

. M for all n $ N. For these values

of n, we have



2 0



, ε;

which establishes the asserted limit.

THEOREM 1

Let α and r be any real numbers. Assume that a and p are

positive. Then:

a. lim

n-N

α 5 α:

b. lim

n-N

5 N:

c. lim

n-N

1=n

5 0:

d. If jrj . 1, then the sequence fr

n51

diverges, and lim

n-N

jrj

5 N.

e. If jrj , 1; then lim

n-N

5 0:

f. lim

n-N

1=n

5 1.

Each conclusion of Theorem 1 is intuitively clear. For example, part a tells us

that a constant sequence converges to that constant. Part b states that, as n grows

without bound, so does any positive power of n. Part d states that when a number

greater than 1 is raised to successi vely higher expo nents, then the resulting powers

grow without bound. Parts c and e follow from parts b and d, using Example 5. The

next example illustrates the use of Theorem 1.

⁄ EX

AMPLE 6 Discuss the convergence of f1=

ﬃﬃﬃ

g; f

ﬃﬃﬃ

100

g; fð299=100Þ

and fð101=100Þ

Solution Theorem

1 can be applied to each of these sequences. The sequence

f1=

ﬃﬃﬃ

g converges to 0 by Theorem 1c with p 5 1=2. We write

ﬃﬃﬃ

100

5 n

1=100

and

conclude that f

ﬃﬃﬃ

100

g diverges to inﬁnity by using Theorem 1b with p 5 1=100: The

sequence fð299=100 Þ

g can be written as fr

g with r 5299=100: Because

jrj5 99=100 , 1, we conclude that the sequence fð299=100Þ

g converges to 0 by

Theorem 1e. Finally, we write fð101=100Þ

g as fr

g with r 5 101=100 . 1: This

sequence tends to inﬁnity by Theorem 1d.

INSIGHT

A numerical investigation of the convergence of a sequence requires some

caution. The evaluations ð101=100Þ

5 1:6446 ::: and ð101=100Þ

150

5 4:4484 ::: hardly

suggest that the sequence fð101=100Þ

g tends to inﬁnity. As the table indicates, it is

necessary to calculate ð101=100Þ

for rather large values of n to obtain convincing

numerical evidence.

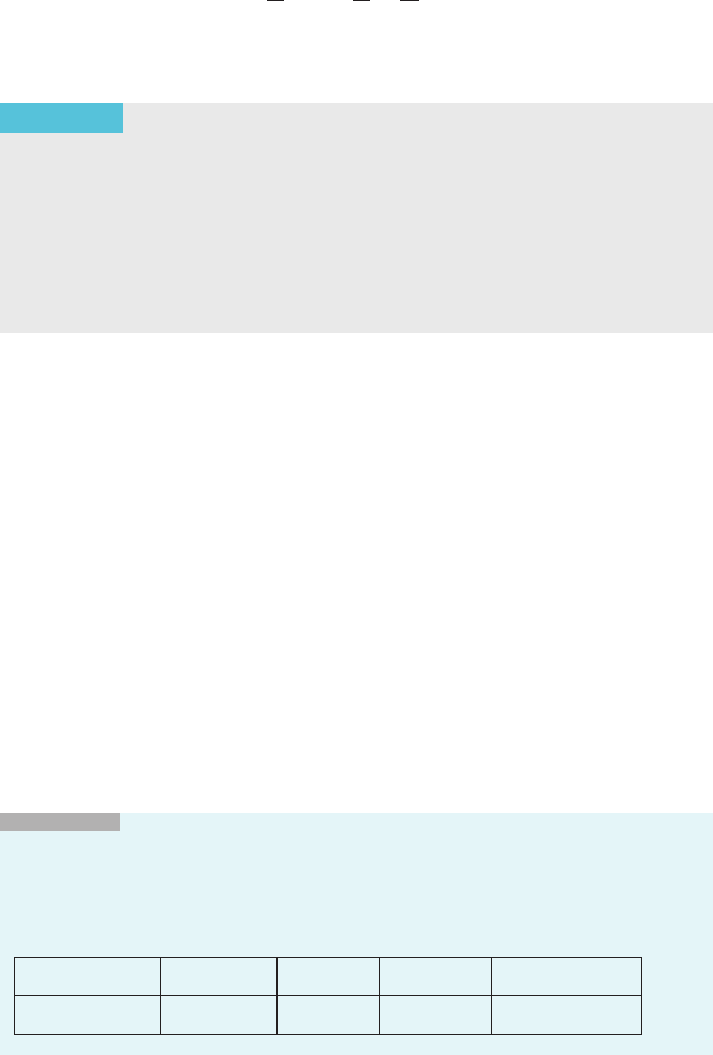
n 200 500 1000 10000

(101/100)

7.3160 1000 20959 1.6358 3 10

130 Chapter 2 Limits

Limit Theorems There are a few rules that enable us to easily evaluate the limits of many common

sequences. The limit rules for the sequences that follow are similar to the limit rules

for the functions in Section 2.2.

THEOREM 2

Suppose that fa

n51

and fb

n51

are convergent sequences.

Then

a. lim

n-N

ða

1 b

Þ5 lim

n-N

1 lim

n-N

b. lim

n-N

ða

2 b

Þ5 lim

n-N

2 lim

n-N

c. lim

n-N

ða

 b

Þ5 ðlim

n-N

Þðlim

n-N

Þ.

d. lim

n-N

lim

n-N

lim

n-N

; provided that lim

n-N

6¼ 0.

e. lim

n-N

α  a

5 α  lim

n-N

for any real number α.

f. lim

n-N

is unique.

From now on, we will usually calculate the limit of a sequence by using The-

orem 2, together with the known limits of several basic sequences, such as those

given in Theorem 1. Although we will not explicitly mention Theorem 2f, we will

use it frequently, because it shows that if we calculate a limit by any particular

method, the answer will be the same as the answer obtained by a different method.

⁄ EX

AMPLE 7 Use Theorem 2 to analyze the limit

lim

n-N

1 4n 2 6

1 2n

Solution The

numerator and the denominator of this limit become ever larger

with n. Ther efore fn

1 4n 2 6g and f3n

1 2ng are not convergent sequences, and

Theorem 2d cannot be applied directly. Before calling on Theorem 2, we divide the

numerator and denominator by the largest power of n that appears (namely, n

lim

n-N

1 4n 2 6

1 2n

5 lim

n-N

1 1 4n

2 6n

3 1 2n

lim

n-N

ð1 1 4n

2 6n

lim

n-N

ð3 1 2n

Theorem 2d

lim

n-N

1 1 4  lim

n-N

2 6  lim

n-N

lim

n-N

3 1 2 lim

n-N

Theorem 2a; 2b and 2e

1 2 4  0 1 6:0

3 1 2  0

Theorem 1a

: Simplify ¥

INSIGHT

If the graph of a function f has a horizontal asymptote y 5 ‘ as x-N, then

the sequence fa

g deﬁned by a

5 f ðnÞ satisﬁes

lim

n-N

5 lim

n-N

f ðnÞ5 lim

x-N

f ðxÞ5 ‘:

2.5 Limits of Sequences 131

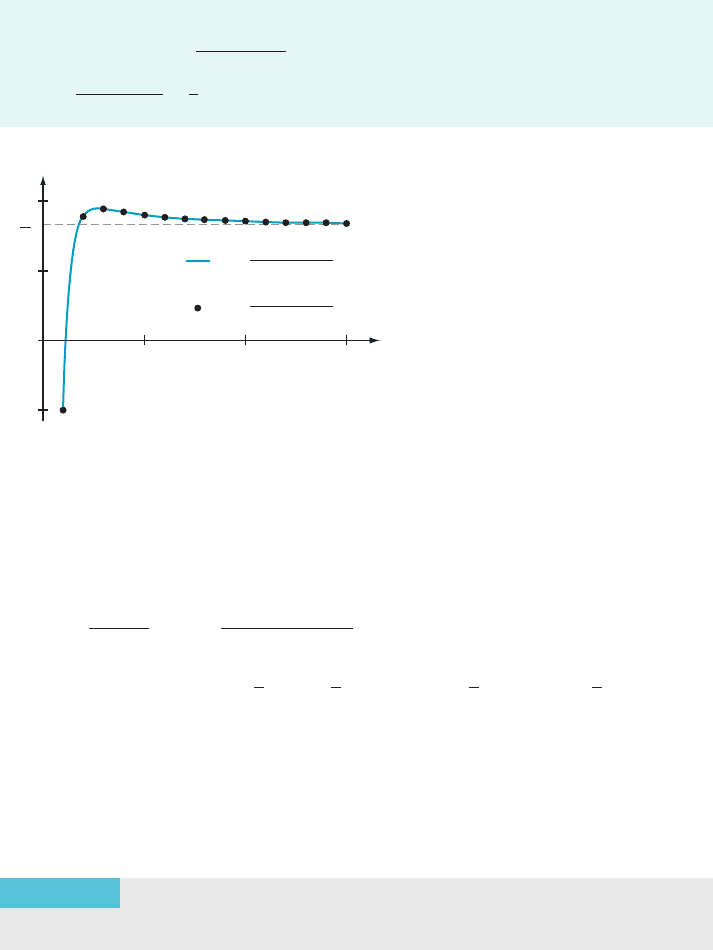
In other words, fa

g has limit ‘. We know from the Insight following Example 6 of

Section 2.4 that f ðxÞ5

1 4x 2 6

1 2x

has y 5 1/3 as a horizontal asymptote. Therefore

lim

n-N

1 4n 2 6

1 2n

(see Figure 4).

⁄ EXAMPLE 8 Calculate lim

n-N

ð2

1 3

Þ=4

Solution We

begin by dividing the numerator and denominator by the largest

term, 4

. Using Theorem 2a, we obtain

lim

n-N

1 3

5 lim

n-N

ð2=4Þ

1 ð3=4Þ

ð4=4Þ

5 lim

n-N









5 lim

n-N





1 lim

n-N





Each of these limits is 0 by Theorem 1e. The requested limit is therefore 0 as

well.

Our next theorem is the analogue for sequences of Theorem 6 from Section 2.2.

THEOREM 3

(Pinching Theorem for Sequences). If lim

n-N

5 lim

n-N

5 ‘

and a

# c

# b

for all n, then lim

n-N

5 ‘:

⁄ EX

AMPLE 9 Evaluate lim

n-N

sinðnÞ=n

Solution Let a

521=n

, b

5 1=n

,andc

5 sinðnÞ=n

. Theorem 1c with p 5 2 tells

us that lim

n-N

5 0. Theorem 2e with α 521 then tells us that lim

n-N

2lim

n-N

5 0. Because 21 # sinðnÞ # 1; we see that a

# c

# b

(see Figure 5).

It follows from the Pinching Theorem that c

5 sinðnÞ=n

has the same limit, 0, when n

tends to inﬁnity.

10 155

0.2

0.2

0.4

y  1/3

y 

 4x  6

 2x



 4n  6

 2n

m Figure 4

132 Chapter

2 Limits

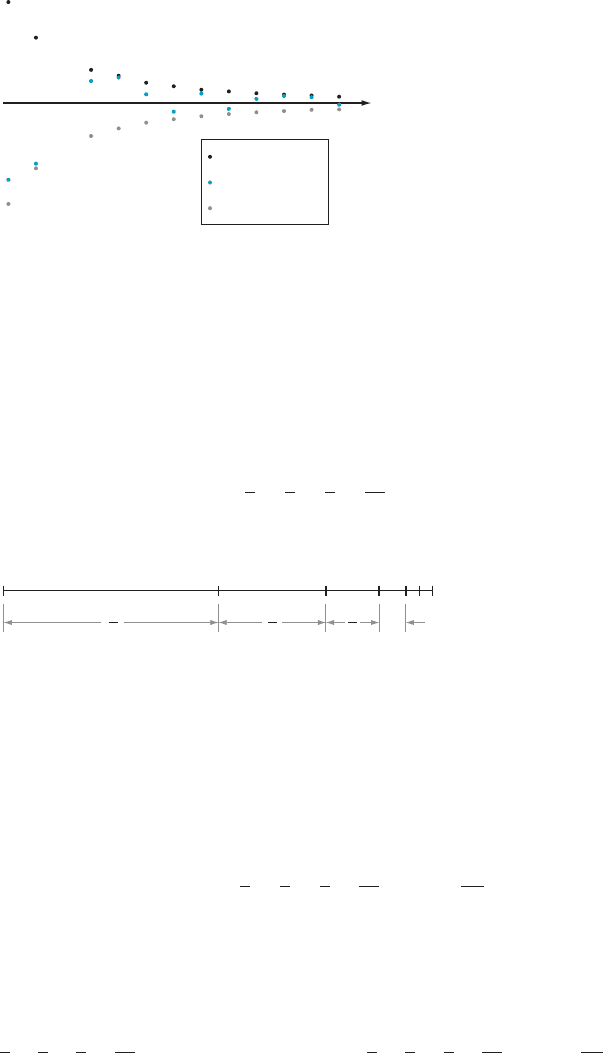
Geometric Series Suppose that an arrow is shot at a target 10 meters away. (That distance is 1 dkm.)

Before hitting its target, the arrow must ﬁrst travel 1/2 the distance, followed by 1/2

the remaining distance (or 1/4 dkm), and then 1/2 the remaining distance (or 1/8

dkm), and so on (see Figure 6). By this reasoning, we conclude that the distance the

arrow travels is 1/2 1 1/4 1 1/8 1 1/16 1 (without end) dkm. On the other hand,

when it hits the target, the distance the arrow has traveled is 1 dkm. In other words,

it appears that

1 5 1:

Before we can make sense of such an equation, we must give the left side a precise

meaning. We certainly do not assert that inﬁnitely many numbers are added up in

the usual fashion on the left. After all, how could such an inﬁnite sum be accom -

plished? What we can do is add the N numbers

1 1

for any positive inte ger N, no matter how large. In other words, we can form the

inﬁnite sequence fs

N51

where s

5 1=2 1 1=4 1 1=8 1 1=16 1 1 1=2

.Ifwe

can show that lim

N-N

exists, then we can deﬁne 1=2 1 1=4 1 1=8 1 1=16 1 to

be this limit:



5 lim

N-N

5 lim

N-N







ð2:5:1Þ

Our discussion suggests that this limit exists and is equal to 1. The next theorem will

allow us to verify our conclusion (in Example 10).

 1/n

 sin (n)/n

 1/n

m Figure 5

1/2

3/4 7/8 1



1         

. . .

m Figure 6

2.5 Limits of Sequences 133

THEOREM 4

Suppose that r 6¼ 1:

a. For each positive integer N

1 1 r 1 r

1 1 r

N21

2 1

r 2 1

: ð2:5:2Þ

b. If jrj, 1 ; then

lim

N-N

ð1 1 r 1 r

1 1 r

N21

Þ5

1 2 r

: ð2:5:3Þ

Proof. We

calculate

ðr 2 1Þð1 1 r 1 r

1 1 r

N21

Þ 5 r ð1 1 r 1 r

1 1 r

N21

2 1 ð1 1 r 1 r

1 1 r

N21

5 r 1 r

1 r

1 1 r

N21

1 r

2 ð1 1 r 1 r

1 1 r

N21

Þ:

We see that each of the terms r, r

, :::, r

N21

appears twice on the right side: once

with a 1 sign and once with a 2 sign. After cancellation, only the terms r

and 21

remain on the right side. Thus we are left with

ðr 2 1Þð1 1 r 1 r

1 1 r

N21

Þ5 r

2 1:

Dividing each side of this identity by r  1, which is nonzero, we obtain (2.5.2).

For the second assertion, we have

lim

N-N

ð1 1 r 1 r

1 1 r

N1

Þ 5 lim

N-N

2 1

r  1

Part a

r  1

 lim

N-N

r 2 1

Theorem 2 a; e; f

r 2 1

 0 2

r  1

Theorem 1e

1 2 r

Simplify: ’

The left sides of formulas (2.5.2) and (2.5.3) are called geometr

ic series. Notice

that geometric series arise by adding the terms of a geometric progression 1, r,

, r

....

⁄ EX

AMPLE 10 Verify that

1 5 1:

Solution Let c

5 1=2 1 1=4 1 1=8 1 1 1=2

: According to deﬁnition (2.5.1),

we must show that lim

N-N

5 1: Observe that for r 5 1/2,

1 1

5 r 1 r

1 r

1 1 r

5 ð1 1 r

1 r

1 1 r

N21

Þ1 ðr

2 1Þ5 a

1 b

;

134 Chapter 2 Limits