Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

2.1 The Concept of Limit

This section includes a number of examples that informally explore the idea of

limit. The understanding of limits gained by reading this section is intuitive, but it is

adequate for most purposes in calculus. Section 2.2 presents a precise formulation

of the limit concept.

Informal Deﬁnition of Limit

Let f be a real-valued function that is deﬁned in an open interval to the left of a real number c and in an open

interval to the right of c. We say, “f (x) has the limit ‘ as x tends to c,” and we write

lim

x-c

f ðxÞ5 ‘;

if the values f (h) are close to ‘ when x is close to, but not equal to, c. As an alternative, we sometimes write

f ðxÞ-‘ as x-c

and say “f (x) tends to ‘ as x tends to c” (see Figure 1).

⁄ EX

AMPLE 1 Let f, g,andh be the three functions deﬁned by

f ðtÞ5 t

for all t; gðtÞ5 t

for all t 6¼ 0; an d hðtÞ5

(

if t 6¼ 0

1ift 5 0

Discuss the limits of f (t), g(t), and h(t)ast approaches 0.

Solution When jtj, 1 ; we

have t

5 jtjjtj, 1 jtj5 jtj. Thus, when jtj is less than 1

(as is ultimately the case when t approaches 0), the number f ðtÞ5 t

is even closer

to 0 than j tj is (see Figure 2). We concl ude that, as t approaches 0, so does f (t). We

write this as lim

t-0

f ðtÞ5 0.

Next, we consider g.

The fact that 0 is not in the domain of g does not affect

whether g( t) has a limit at t 5 0. For t 6¼0, we have gðtÞ5 t

, and our calculation of

the limit of f ðtÞ at t 5 0 allows us to conclude that lim

t-0

gðtÞ5 lim

t-0

5 0.

Finally, we turn to the function h. The deﬁnition of “limit” tells us that the

equation h(0) 5 1 has nothing to do with the existence or value of lim

t-0

hðtÞ.When

0.8

0.4

1.00.51.0 0.5

y  t

y  t

m Figure 2

f (x)

ᐉ

x → c ← x

→

m Figure 1 f (x) has the limit ‘ as x tends to c

INSIGHT

The value f (c)

plays no role in the deﬁnition

of the limit of f (x)asx tends

to c.Wedonot even assume

that f is deﬁned at c. Indeed,

a deﬁnition of “limit” that

required f to be deﬁned at c

would not be relevant to many

important applications. Even

when f (c) is deﬁned, the value

f (c) does not have to be

related to lim

x-c

f ðxÞ in any

way. In a sense, lim

x-c

f ðxÞ is

what we anticipate that f (x)

will equal at x 5 c, not

necessarily what f (x) actually

equals when x 5 c.

2.1 The Concept of Limit 85

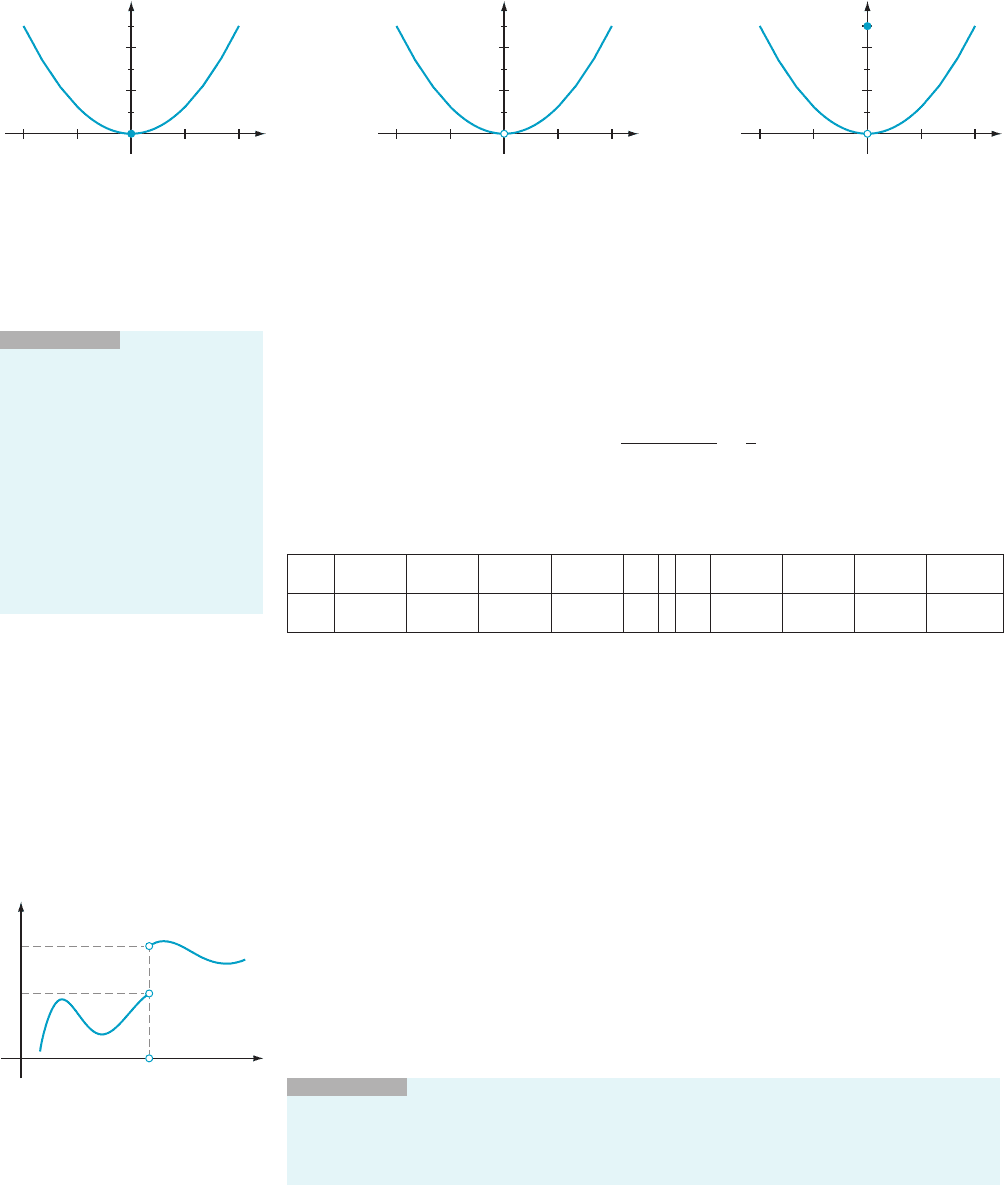
t is near 0 but unequal to 0, we have hðtÞ5 t

. Therefore lim

t-0

hðtÞ5 lim

t-0

5 0.

Figure 3 illustrates the three limits that we have calculated.

⁄ EXAMPLE 2 Let f ðxÞ5 ðx

2 6x 1 6Þ=x. Evaluate lim

x-5

f ðxÞ.

Solution We

look at the components of f.Asx tends to 5, the expression x

tends

to 25, and the expression 6x tends to 30. We conclude that

lim

x-5

f ðxÞ5

25 2 30 1 6

A numerical inves tigation, as shown in the table, supports this conclusion.

Approach from the left side of 5 Approach from the right side of 5

x 4.99 4.999 4.9999 4.99999 - 5 ’ 5.00001 5.0001 5.001 5.01

f (x) 0.19240 0.19924 0.19992 0.19999 . . . . . . 0.20000 0.20008 0.20076 0.20760

The actual value of f (x) for x 5 5 has been intentionally omitted from the table.

It is not used in the investigation of the limiting value of f (x)asx approaches 5.

One-Sided Limits Implicit in the limit deﬁnition is the fact that a function should have just one limit at a

point c. Suppose that f (x) is close to a number ‘

when x is close to c and to the left

of c, and that f (x) is close to a different number ‘

when x is close to c and to the

right of c. We say that f has a left limit ‘

at c and a right limit ‘

at c, but we do not

say that f has a limit at c (see Figure 4). These one-sided limits are written as

lim

x-c

f ðxÞ5 ‘

(or f ðxÞ-‘

as x-c

) for the left limit and lim

x-c

f ðxÞ5 ‘

(or

f ðxÞ-‘

as x-c

) for the right limit. From these informal deﬁnitions, it is clear that

lim

x-c

f ðxÞ5 ‘ is equivalent to



lim

x-c

f ðxÞ5 ‘

; lim

x-c

f ðxÞ5 ‘

; and ‘

5 ‘



In other words, if both left and right limits exist and are the same, then the limit

does exist.

INSIGHT

The notation for one-sided limits arises from the c 5 0 case. As x

approaches 0 from the left, x assumes negative values; hence, x - 0

.Asx approaches 0

from the right, x assumes positive values; therefore, x-0

. Keep this in mind to help

remember the notation.

y  f(t)

0.8

0.4

1.00.51.0 0.5

m Figure 3a lim

t-0

f ðtÞ5 0

y  g(t)

0.8

0.4

1.00.51.0 0.5

m Figure 3b lim

t-0

gðtÞ5 0

y  h(t)

0.8

0.4

1.00.51.0 0.5

m Figure 3c lim

t-0

hðtÞ5 0

ᐉ

x→c





←x

m Figure 4 lim

x-c

f ðxÞ5 ‘

lim

x-c

f ðxÞ5 ‘

INSIGHT

In Example 2,

we used the plausible idea that

the limit of a sum or difference

is the sum or difference of the

limits, the limit of a product is

the product of the limits, and

the limit of a quotient is the

quotient of the limits (as long

as we do not divide by zero).

These limit properties are

treated in more detail in

Section 2.2.

86 Chapter 2 Limits

⁄ EXAMPLE 3 Let H and G be deﬁned by

HðxÞ5

1ifx , 3

2ifx $ 3

and GðsÞ5

1 1ifs , 4

5s 2 3ifs . 4



Does H(x) have a limit as x tends to 3? Does G(s) have a limit as s tends to 4?

Solution Refer

to Figure 5 for the graph of H.Asx approaches (but does not

equal) 3 from the left, H(x) tends to 1. On the other hand, as x approaches (but

does not equal) 3 from the right, H(x) tends to 2. Thus lim

x-3

HðxÞ5 1; and

lim

x-3

HðxÞ5 2. However, H(x) does not have a limit as x tends to 3 because there

is no single value that H(x) approaches as x tends to 3.

When s is

near 4 but to the left of 4, s

is near 16, and s

1 1 is near 17. Thus

lim

s-4

GðsÞ5 17. On the other hand, when s is near 4 but to the right of 4, 5s is

near 20, and 5s  3 is near 17. Hence lim

s-4

GðsÞ5 17. Because G(s) tends to 17

both from the left and the right, we can say that lim

s-4

GðsÞ5 17. This limit can also

be seen from the graph of G (see Figure 6).

Limits Using Algebraic

Manipulations

In many situations, some algebraic manipulations are required in order to evaluate

a limit.

⁄ EX

AMPLE 4 Does

f ðxÞ5

2 4

x 1 2

have a limit as x approaches 22?

Solution This

type of limit often occurs in calculus. The function f is not deﬁned at

the point where the limi t is being calculated. We therefore cannot atte mpt a

shortcut by simply substituting x 522. Instead, we attack this problem by noticing

that

f ðxÞ5

ðx 1 2Þðx 2 2Þ

ðx 1 2Þ

As long as x 6¼ 22, then x 1 2 6¼ 0. We can divide this common nonzero factor

from the numerator and denominator. As a result, f ðxÞ5 x 2 2 when x 6¼ 22:

Remember that, in calculating the limit of f at 2 2, we consider the values of f (x)

for x close to, but not equal to, 22. Therefore, as x- 22; f (x) tends to the same

limit as x 2 2 does. In summary,

lim

h- 22

2 4

x 1 2

5 lim

x- 22

ðx 2 2Þ524:

Refer to Figure 7.

Speciﬁed Degrees of

Accuracy

We turn now to a practical, computation-oriented approach to the limit concept. By

lim

x-c

f ðxÞ5 ‘, we mean that f (x) tends to ‘ when x tends to c. Now we ask: How

close does x need to be to c to force f (x) to stay within 0.1 of ‘ ? How close does x

need to be to c to force f (x) to stay within 0.01 of ‘? and so on.

6422

m Figure 5 HðxÞ5

1ifx , 3

2ifx $ 3



8462

lim G(s)  17

s→4

m Figure 6

GðsÞ5

1 1ifs , 4

5s 2 3ifs . 4



4642

8

6

f(x) 

 4

 2

m Figure 7

2.1 The Concept of Limit 87

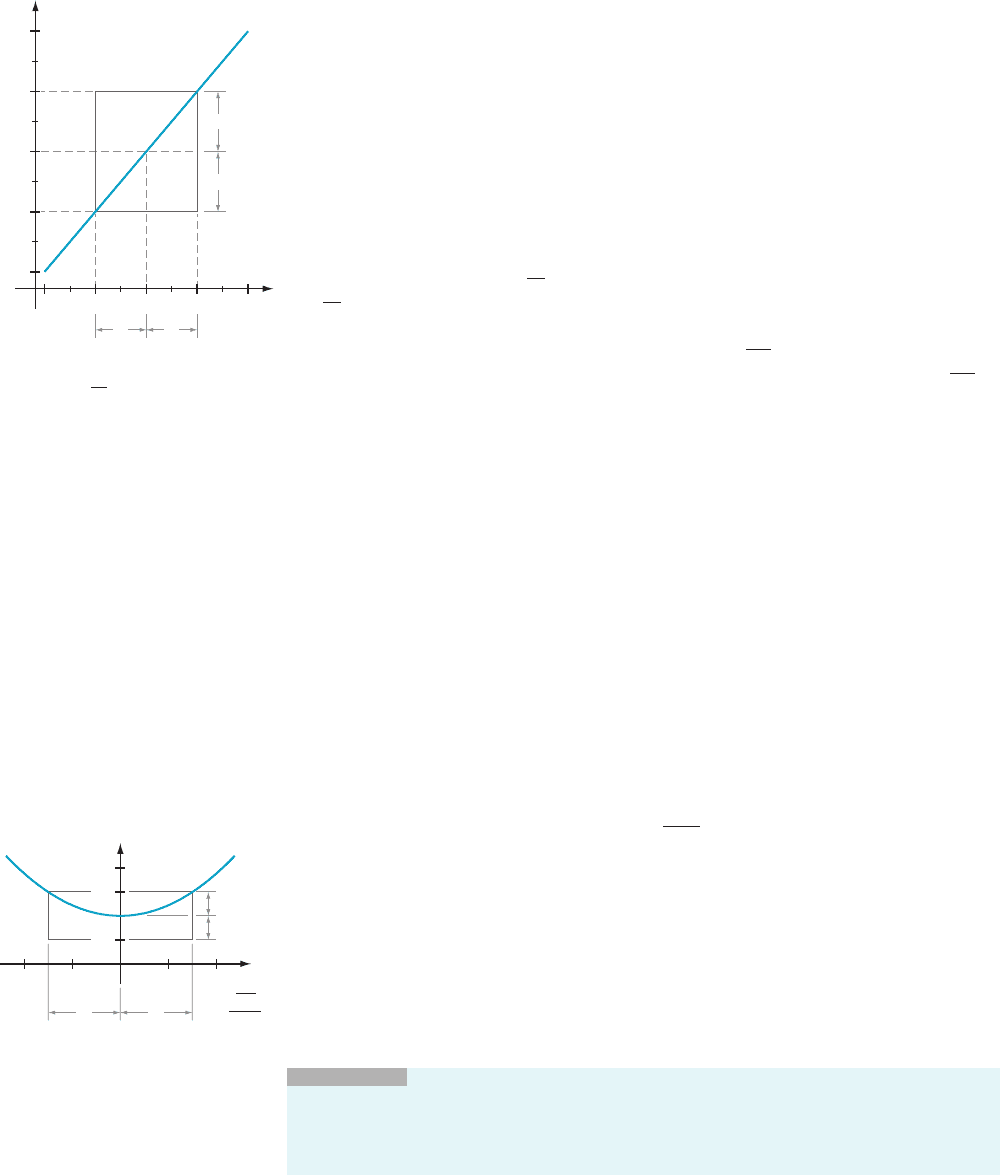
This method of thinking about limits is important for applications and also

leads to a deeper understanding. In the examples that follow, the bound on the

desired distance of f (x)to‘ is called ε. The required distance of x to c is called δ.

⁄ EX

AMPLE 5 If x is close to 4, then f (x) 5 3x 1 2 is close to 14. We

therefore say that lim

x-4

f ðxÞ5 14. How close must x be to 4 to force f (x) 5 3x 1 2

to be within 0.1 of 14? Within 0.01 of 14?

Solution We

will denote the limit, 14, by ‘. To force f (x) 5 3x 1 2 to within ε 5 0.1

of ‘, we solve the inequality jf ðxÞ2 ‘j, ε,orjð3x 1 2Þ2 14j, 0:1, or j3x 2 12j, 0:1:

The solution is obtained by multiplying both sides of the last inequality by 1/3,

which gives us jx 2 4 j ,

0:1

5 0:0333 :::. Therefore provided x stays within

δ 5

0:1

5 0:0333 ::: of c 5 4, f ( x ) will stay within ε 5 0.1 of ‘ 5 14 (see Figure 8).

Similarly, to make f (x) stay within ε 5 0.01 of ‘ 5 14, we solve the inequality

jð3x 1 2Þ2 14j, 0:01: The solution is jx 2 4j,

0:01

5 0:00333 :::. Ther efore

f (x) 5 3x 1 2 stays within ε 5 0.01 of ‘ 5 14, provided that x stays within δ 5

0:01

0.00333 . . . of c 5 4. There is clearly a pattern here. If we want to make

f ðxÞ5 3x 1 2 stay within a certain distance ε of ‘ 5 14, then we restrict x to lie

within δ 5 ε=3ofc 5 4. We can achieve any desired degree of accuracy by taking ε

as small as we like. Our calculation offers compelling evidence of a quantitative

nature that justiﬁes the intuitive feeling that lim

x-4

ð3x 1 2Þ5 14. ¥

⁄ EXAMPLE 6 Let f ðxÞ5 x

1 4. How close to 0 does x have to be to force

f (x) to be within ε 5 0.1 of ‘ 5 4?

Solution Although

it is intuitively clear that lim

x-0

f ðxÞ5 4, let us examine the

matter from the point of view of approximation, as in Example 5. To force

f ðxÞ5 x

1 4 to be within ε 5 0.1 of ‘ 5 4, we solve the inequality

jf ðxÞ2 4j, 0:1:

The

solution is jðx

1 4Þ2 4j, 0:1, or j x

j, 0:1 5 10=100, or jxj,

ﬃﬃﬃﬃﬃ

=10. Because

we are interested in the distance of x from 0, we write

jx 2 0j,

ﬃﬃﬃﬃﬃ

Thus f ðxÞ5 x

1 4 is within ε 5 0.1 of ‘ 5 4 when x is within δ 5

ﬃﬃﬃ

ﬃﬃﬃﬃﬃ

=10 of

c 5 0 (see Figure 9). We arrive at our conclusion by working backward from the

desired estimate on the function x

. Let us now check our work: If jx 2 0j,

ﬃﬃﬃﬃﬃ

=10;

then jx

j, 10 = 100, or jðx

1 4Þ2 4j, 0:1. This means that jf ðx Þ2 4j, 0:1, which is

the desired result. Once we become accustomed to this process, we can work

backward with conﬁdence and not bother to check the work by repeating the

calculation in the forward direction.

INSIGHT

The degree of closeness for x to c in Example 6 (namely, δ 5

ﬃﬃﬃ

)is

different from that in Example 5 (namely, δ 5 ε=2). Different functions approach their

limits at different rates. This will be one of the main points in the limit problems that

we study.

14.2

14.1

14.0

13.9

13.8

3.966... 4.00 4.033... 4.066...

␦ ␦

f(x)  3x  2

ᐉ

⑀  0.1

m Figure 8

ε 5 0.1, δ 5

0:1

5 0.0333 . . .



0.2 0.40.4 0.2

3.9

4.1

4.2

e  0.1

dd 

m Figure 9

88 Chapter

2 Limits

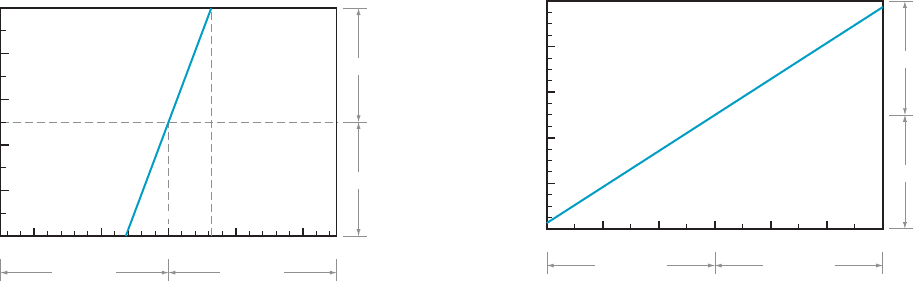
Graphical Methods Examples 5 and 6 provide algebraic solutions to the question, “For a given small

number ε, how can we take x close enough to c to force f (x)tobewithinε of ‘?” We

may also answer this question by graphical methods. Indeed, the condition that f (x)

stays within ε of ‘ when x stays within δ of c is easily visible when we plot f in the

viewing rectangle: ½c 2 δ; c 1 δ 3 ½‘ 2 ε;‘1 ε: The graph exits the window only

through the lateral sides—not through the top or bottom of the viewing window.

⁄ EX

AMPLE 7 Let f ðxÞ5 ðx

2 6x 1 6Þ=x. In Example 2, we observed that

lim

x-5

f ðxÞ5 1=5. Find a positive number δ such that f (x) stays within 0.01 of 1/5

when x stays within δ of 5.

Solution In

this example, we set c 5 5, ‘ 5 1/5, and ε 5 0.01. We begin by making an

arbitrary choice of δ: δ 5 0:05. Figure 10 shows the graph of f in the viewing window

½5 2 0:05; 5 1 0:053 ½1=5 2 0:01; 1=5 1 0:01. Because the graph of f exits this window

through its top and bottom, we must use a smaller value for δ . To determine such a

value, we observe that, on the horizontal axis in Figure 10, the distance between

tick marks is 0.004. From the plot, we can see that f (x) stays within ε 5 0.01 of ‘ 5 1/5,

provided that x stays within 3 3 0:004 of c 5 5. We therefore set δ 5 0.012.

The resulting graph of f in the viewing rectangle ½5 2 0:012; 5 1 0: 0123

½1=5 2 0:01; 1= 5 1 0:01 sh

ows that our choice δ 5 0:012 sufﬁces (see Figure 11). ¥

Some Applications of

Limits

Numerical calculations of the type we have been examining come up frequently in

applications. Following are some examples.

⁄ EX

AMPLE 8 An unmanned spacecraft is to be sent to a distant planet. The

ground control personnel compute that an error of size d degrees in the spacecraft’s

initial angle of trajectory will result in the spacecraft missing its target by

EðdÞ5 30 ð10

2 1Þ miles. The spacecraft must land within 0.1 mile of its target for

the mission to be considered successful. What error in the measurement d of the

trajectory angle is allowable?

Solution To

answer this question, we require 30 ð10

2 1Þ, 0:1. This inequality

is equivalent to 10

2 1 , 1=300; or 10

, 1 1 1=300. The solution set is d ,

log

ð1 1 1= 300Þ0:00144524073. Thus d 5 0:00144 will sufﬁce. Trajectory angle

e  0.01

4.95

0.210

0.190

0.206

0.202

0.198

0.194

4.96 4.98 5.05

y  ᐉ

d  0.05 d  0.05

x  c

5.00 5.02 5.04

m Figure 10 Viewing rectangle

½5 2 δ; 5 1 δ3 ½1=5 2 ε; 1=5 1 ε

4.988 4.992 4.996

0.210

0.190

0.206

0.202

0.198

0.194

5.000 5.004 5.008 5.012

d  0.012 d  0.012

e  0.01

m Figure 11 Viewing rectangle

½5 2 δ; 5 1 δ3 ½1=5 2 ε; 1=5 1 ε for a smaller δ.

2.1 The Concept of Limit 89

measurements on this ﬂight can be measured to within an accuracy of 0.00144

degrees without affe cting the success of the mission (see Figure 12).

⁄ EXAMPLE 9 In a controlled reaction of hydrogen with bromine, the rate R

at which hydrogen bromide is produced (in moles per liter per second) is given by

RðcÞ5 0:08

ﬃﬃﬃ

where c is the concentration of bromine (in moles per liter). How

close to 0.16 must the bromine concentration be maintained to ensure that the rate

of production of hydrogen bromide is within 0.001 of 0.032? Answer in the form of

an interval ð0:16 2 δ; 0:16 1 δÞ.

Solution We

require that j0:08

ﬃﬃﬃ

2 0:032j, 0:001. From the Insight following

Example 3, Section 1.1, we see that this inequality is equivalent to 20:001 ,

0:08

ﬃﬃﬃ

2 0:032 , 0:001, or, after adding 0.032 to each side, 0:031 , 0:08

ﬃﬃﬃ

, 0:033.

Dividing by the positive number 0.08 results in 0:3875 ,

ﬃﬃﬃ

, 0:4125. Finally, by

squaring each side, we obtain 0:15015625 , c , 0:17015625. Let δ

5 0:16 2

0:15015625 5 0:00984375, and δ

5 0:17015625 2 0:16 5 0:01015625. We have

found that RðcÞ is within 0.001 of 0.032 for c in the interval I 5 ð0: 16 2 δ

;

0:16 1 δ

Þ. The interval ð0:16 2 δ; 0:16 1 δÞ we seek must be contained in I and

centered at 0.16. We therefore take δ to be the smaller of δ

and δ

: δ 5

0:00984375. In summary, the rate of production of hydrogen bromide is within

0.001 of 0.032 when the concentration of bromine is within 0.00984375 of 0.16.

A plot of R(c) in the viewing window ½0:16 2 0:00984375; 0 :16 1 0:009843753

½0:032 2 0:001; 0:032 1 0: 001 conﬁrms our analysis (see Figure 13).

0.10

0.08

0.06

0.04

0.02

0.0004

E(d)  30ⴢ (10

 1)

x  0.00144

Allowable Inaccuracy

0.0008 0.0012

m Figure 12

0.033

0.032

0.031

0.16

R(c)  0.08 c

0.00984375 0.00984375

0.001



m Figure 13

90 Chapter

2 Limits

QUICK QUIZ

1. True or false: lim

x-0

f ðxÞ can exist even if f does not have the point 0 in its

domain.

2. Calculate lim

t-5

ðt

1 25Þ=ðt 1 5Þ.

3. Calculate lim

t-5

ðt

2 25Þ=ðt 2 5Þ.

4. How close must a positive number x be to 2 to ensure that x

is within 1/100 of 4?

Answers

1. True 2. 5 3. 10 4 .

ﬃﬃﬃﬃﬃﬃﬃ

ﬃ

401

=10 2 2

EXERCISES

Problems for Practice

c In Exercises 128, decide whether the indicated limit

exists. If the limit does exist, compute it. b

1. lim

x-2

ðx 1 3Þ

2. lim

s-9

ðs

2 6s 1 10Þ

3. lim

h-4

ð3h

1 2h 1 1Þ

4. lim

s-0

ð2 1 sÞ=s

5. lim

h-1

h 2 3

h 1 1

6. lim

x-23

x 2 3

2 9

7. lim

x-2

gðxÞ for

gðxÞ5

4ifx , 0

24ifx $ 0



8. lim

x-21

f ðxÞ for

f ðxÞ5

6ifx #21

10 if x .21



c In Exercises 9214, some algebraic manipulation is neces-

sary

to determine whether the indicated limit exists. If the

limit does exist, compute it and supply reasons for each step

of your answer. If the limit does not exist, explain why. b

9. lim

x-5

ðx

2 25Þ

ðx 2 5Þ

10. lim

t-7

ðt 1 7Þ

ðt

2 49Þ

11. lim

t-27

ðt 1 7Þ

ðt

2 49Þ

12. lim

h-0

ðh

1 h

ðh

2 3h

13. lim

x-24

ðx

1 6x 2 8Þ

ðx

2 2x 2 24Þ

14. lim

x-23

ðx

2 9Þ

ðx 1 3Þ

c In Exercises 15218, determine if lim

x-c

f ðxÞ exists. Con-

sider separately the values f takes when x is to the left of c and

the values f takes when x is to the right of c. If the limit exists,

compute it. b

15. f ðxÞ5

2 3x if x , 2

x 2 1

if x $ 2

c 5 2

16. f ðxÞ5

1 6x 2 7

2 1

if x , 1

ðx12Þ

if x $ 1

c 5 1

17. f ðxÞ5

2 4

if x # 5

2 3x 2 10

2 9x 1 20

if x . 5

c 5 5

18. f ðxÞ5

2 9

1 9

if x # 3

ðx23Þ

2 9

if x . 3

c 5 3

c In Exercises 19226, calculate how close x needs

to be to c

to force f (x) to be within 0.01 of ‘. b

19. f ðxÞ5 x 1 1; c 5 2;‘5 3

20. f ðxÞ5 2x 2 3; c 522;‘527

21. f ðxÞ5 5x 1 2; c 5 3;‘5 17

22. f ðxÞ5 x

2 1; c 5 0;‘521

23. f ðxÞ5 5 2 x

=4; c 5 0;‘5 5

24. f ðxÞ5 1 1

ﬃﬃﬃﬃﬃﬃﬃ

jxj;

c 5 0;‘5 4

25. f ðxÞ5

x if x , 1

10x 2 9ifx # 1

c 5 0:999;‘5 0:999



26. f ðxÞ5

4x 2 3ifx # 1

x if x . 1

c 5 1;‘5 1



c In Exercises 27

and 28, demonstrate that the limit does not

exist by considering one-sided limits. b

27. lim

x-2

f ðxÞ where

f ðxÞ5

2 4

x 1 2

if x # 2

2 4

x 2 2

if x . 2

2.1 The Concept of Limit 91

28. lim

x-25

f ðxÞ where

f ðxÞ5

4x if x #25

3x 2 4ifx .25



Further Theory and Practice

c In Exercises 29232, you are given four functions f, g, h,

and k, and a point c. b

a. State

the domain of each function.

b. Identify two of these functions that are the same.

Explain why. In what way do the other functions differ

from these two functions?

c. For each function, decide if it has a limit at c. Identify

the limit if it exists.

29. gðxÞ5

2 1

x 2 1

; hðxÞ5

2 1

x 2 1

if x 6¼ 1

2ifx 5 1

f ðxÞ5 x 1 1; kðxÞ5

2 1

x 2 1

if x 6¼ 1

1ifx51

c 5 1

30. f ðxÞ5

1 x 2 6

x 2 2

; hðxÞ5

1 x 2 6

x 2 2

if x 6¼ 2

0ifx 5 2

gðxÞ5 x 1 3; kðxÞ5

1 x 2 6

x 2 2

if x 6¼ 2

5ifx 5 2

c 5 2

31. f ðxÞ5

jxj

signumðxÞ

if x 6¼ 0

0ifx 5 0

; hðxÞ5

jxj

signumðxÞ

;

f ðxÞ5

jxj

signumðxÞ

if x 6¼ 0

1ifx 5 0

; kðxÞ5 x; c 5 0

32. f ðxÞ5

(

2 x

if x 6¼ 0

21ifx 5 0

; hðxÞ5

2 x

;

f ðxÞ5

(

2 x

if x 6¼ 0

0ifx 5 0

; kðxÞ5 x 2 1; c 5 0

33. The Heaviside function H(x) is deﬁned by

H 5 ðxÞ

1ifx . 0

0ifx , 0:



Compute lim

x-0

HðxÞ and lim

x-0

HðxÞ. Does

lim

x-0

HðxÞ exist?

34. Suppose a sample of gas is held at constant pressure. Let

denote the volume when the temperature is 0 degrees

centigrade. The Law of Charles and Gay-Lussac relates

the volume V and temperature T (measured in degrees

centigrade) of the given gas sample by the equation

V 5 V

1 V

 T=273: Use this law to show that T belongs

to an interval of the form T . τ. The number τ is known

as absolute zero. Discuss the one-sided limit of V as T

tends to absolute zero.

35. One foot is 0.3048 meter. How precisely should a length

be measured in meters to guarantee accuracy of 0.001

foot?

36. One ounce is 28.350 grams. How precisely should weight

be measured in ounces to guarantee accuracy of

0.001gram?

37. Let bxc be the greatest integer that is less than or equal to x.

For instance, b3=2c5 1; b0c5 0; b2 1=2c521: Discuss

each limit.

a. lim

x-0

bxc

b. lim

x-1=2

bxc

c. lim

x-1

1=bxc

d. lim

x-21=2

1=bxc

38. Let n be an integer. For the greatest integer function bxc

deﬁned in Exercise 37, discuss each limit.

a. lim

x-n

bxc

b. lim

x-n

bxc

c. lim

x-n

bxc

39. Graph the greatest integer function bxc, deﬁned in

Exercise 37. What is the graphical indication that

lim

x-n

bxc does not exist for an integer n?

40. The graph of a function f that is deﬁned on ð1; 4Þ,ð4; 5

appears in Figure 14. Determine all values of c at which

the limit lim

x-c

f ðxÞ exists. Determine all values of c at

which the left limit lim

x-c

f ðxÞ exists. Determine all

values of c at which the right limit lim

x-c

f ðxÞ exists.

61 2 3 4

y  f (x)

m Figure 14

92 Chapter

2 Limits

c In each of Exercises 41 and 42, a particle is moving in

the xy-plane in such a way that it is at the speciﬁed point at

time t. b

a. Compute

the average velocity of the particle from

t 5 1tot 5 2.

b. Compute the average velocity from t 5 1tot 5 1.5.

c. Compute the average velocity from t 5 1tot 5 1.1.

d. Compute the average velocity from t 5 1tot 5 1 1 h

where h is a small nonzero number.

e. What is the limit of these average velocities as h-0?

41. ðt

; 0Þ

42. ð0; 4t

2 3Þ

c In each of Exercises 43246, a particle moves on an axis.

Its

position p(t) at time t is given. For the given value t

and a

positive h, the average velocity over the time interval

½t

; t

1 h is vðhÞ5

pðt

1 hÞ2 pðt

. b

a. Calculate

vðhÞ explicitly, and use the expression you

have found to calculate v

5 lim

h-0

vðhÞ.

b. How small does h need to be for

vðhÞ to be between v

and v

1 0:1?

c. How small does h need to be for

vðhÞ to be between v

and v

1 0:01?

d. Let ε . 0 be a small positive number. How small does

h need to be to guarantee that

vðhÞ is between v

and

1 ε?

43. pðtÞ5 t

1 2; t

5 2

44. pðtÞ5 3t

; t

5 1

45. pðtÞ5 t

1 2t; t

5 3

46. pðtÞ5 1 1 5t 1 t

; t

5 0

c In Exercises 47250, a function f and

a point c are

given. b

a. What

is the slope of the line passing through ðc; f ðcÞÞ

and ðc 1 h; f ðc 1 hÞÞ?

b. What is the limit of these slopes as h-0?

47. f ðxÞ5 x

; c 5 3

48. f ðxÞ5 x

; c 5 2

49. f ðxÞ5 x

1 2x; c 5 1

50. f ðxÞ5 x 2 x

; c 521

51. Discuss lim

x-0

5=3

jxj

52. Discuss lim

x-1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

jx 2 1j

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 1j

Calculator/Computer Exercises

c In each of Exercises 53258, a function f, a point c, and a

positive ε are given. Graphically determine a δ for which f (x)

is within ε of f (c) for every x that is within δ of c. b

53. f ðxÞ5 4=x

; c 5 2; ε 5 0:01

54. f ðxÞ5

ﬃﬃﬃ

; c 5 1; ε 5 0:1

55. f ðxÞ5 x

; c 5 10; ε 5 0:01

56. f ðxÞ5 1=x; c 5 0:2; ε 5 0:01

57. f ðxÞ5 1=

ﬃﬃﬃ

; c 5 9; ε 5 0:01

58. f ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 16

; c 5 3; ε 5 0:01

59. A machinist must do all of his work to within a tolerance

of 10

mm. The calibrations on his machine are such

that if the machinist’s settings are accurate to within m

mm, then the dimensions of the product have a tolerance

within 1:2jmj1 100m

mm. What accuracy of the settings

is required (i.e., how small must the machinist make m)

to produce work of the desired tolerance?

c In Exercises 60264, a function f and

a point c not in the

domain of f are given. Analyze lim

x-c

f ðxÞ as follows. b

a. Evaluate f ðc 2 1=10

Þ and f ðc 1 1=10

Þ for n 5 2; 3; 4.

b. Formulate a guess for the value ‘ 5 lim

x-c

f ðxÞ.

c. Find a value δ such that f (x) is within 0.01 of ‘ for

every x that is within δ of c.

d. Graph y 5 f ð xÞ for x in ½c 2 1=10

; cÞ,ðc; c 1 1=10

 to

verify visually that the limit of f at c exists.

60. f ðxÞ5 sinðxÞ=x; c 5 0

61. f ðxÞ5

cosðxÞ

x 2 π=2

; c 5 π=2

62. f ðxÞ5

sinðxÞ

x 2 π

; c 5 π

63. f ðxÞ5

x 2 sinðxÞ

; c 5 0

64. f ðxÞ5

cosðxÞ2 1

; c 5 0

c In each of Exercises 65268, a particle moves on an

axis.

Its position p(t) at time t is given. For a positive h, the

average velocity over the time interval ½2; 2 1 h is

vðhÞ5

pð2 1 hÞ2 pð2Þ

: b

a. Numerically

determine v

5 lim

h-01

vðhÞ:

b. How small does h need to be for

vðhÞ to be between v

and v

1 0:1?

c. How small does h need to be for

vðhÞ to be between v

and v

1 0:01?

65. pðtÞ5 t

2 8t

66. pðtÞ5 ð2tÞ

3=2

2 2t

67. pðtÞ5 2t 2

cos



πt



68. pðtÞ5 9t

=ðt 1 1Þ

69. A spring moves so that the amount of extension x is given

by xðtÞ5 sinðtÞ. (A negative value of x corresponds to

compression.) In this exercise, you will approximate

the instantaneous velocity vðtÞ of the spring at time t

by its average velocity

vðtÞ over the time interval

½t 2 0:0001; t 1 0:0001.

a. Write

vðtÞ explicitly, and graph vðtÞ for 0 # t # 2π.

b. When, approximately, is

vðtÞ the greatest? The most

negative?

2.1 The Concept of Limit 93

c. When, approximately, is vðtÞ zero?

d. Graph x and

v in the viewing window ½0; 2π3

½21:1; 1:1. For what subinterval I of ½0; 2π is

v , 0?

What is the behavior of x as t increases through this

subinterval I? What does

vðtÞ, 0 mean?

e. Based on the graph of

v, what function does v appear

to approximate?

2.2 Limit Theorems

In Section 2.1, we discussed limits intuitively and numerically. Now we learn a

precise deﬁnition of the statement

lim

x-c

f ðxÞ5 ‘:

It will be written with mathematical symbols, but it will mean “f ðxÞ can be forced

arbitrarily close to ‘ by making x sufﬁcien tly close to c.”

We measure the distance of f ðxÞ to ‘ by the absolute difference jf ðxÞ2 ‘j.

When we say that f ðxÞ can be forced arbitrarily close to ‘, we mean that we can

make jf ðxÞ2 ‘j smaller than ε, no matter how small the positive number ε is. Thus

“f ðxÞ can be forced arbitrarily close to ‘” translates as “for any given positive ε,we

can make jf ðxÞ2 ‘j, ε.”

“By making x sufﬁciently close to c” translates to “we are considering only

those x that lie within a speciﬁed distance δ of c.” In other words, we refer to those

x for which 0 , jx 2 cj, δ.

Now we are ready for the complete deﬁnition.

DEFI NITION

Let f be a real-valued function that is deﬁned in an open interval

just to the left of a real number c and in an open interval just to the right of c.

We say, “The limit of f ðxÞ is equal to ‘ as x approaches c,” and we write

lim

x-c

f ðxÞ5 ‘ if, for any ε . δ , there is a δ . 0 such that

jf ðxÞ2 ‘j, ε

for all values of x such that

0 , jx 2 cj, δ:

The limit can also be written as f ðxÞ-‘ as x-c (see Figure 1).

This deﬁnition is often referred to as the ε-δ deﬁnition of limit. Notice that the

inequality 0 , jx 2 cj, δ means we are considering values of x that are near to c but

not equal to c.Anε-δ veriﬁcation of a limit star ts with the assumption that an

arbitrary positive ε is given. Then a δ corresponding to that ε must be found. This is

exactly what we did in the quantitative examples from Section 2.1 in which speciﬁc

values of ε were given. As you read the next example, notice that we ﬁnd δ in terms

of ε for a general value of ε.

⁄ EX

AMPLE 1 Let f ðxÞ5 3x 1 2. Using the rigorous deﬁnition of limit,

verify that lim

x-4

f ðxÞ5 14.

ᐉ

 e

ᐉ

 e

 f (x)  ᐉ  e

for

0 

 x  c  d

c  dc  d

m Figure 1 f (x) has the limit ‘

as x tends to c

94 Chapter 2 Limits