Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

92. f (t) 5 t

1 t 1 1, g( t) 5 t

2 2t, I 5 [27/4, 3/2]. A point P is

a double point of a parametric curve if there are two

values of t in I such that P 5 ( f (t), g(t)). Find the double

point of the given curve and the two values that para-

meterize that point.

c In Exercises 93 and 94, graph the inverse function of the

given function f. Do not attempt to ﬁnd a formula for f

. b

93. f (x) 5 x

23x

1 x

1 6x28, 0 # x # 2

94. f (x) 5 x

23x

1 3x,0# x # 1

1.6 Trigonometry

When ﬁrst learning trigonometry, we study triangles and measure angles in

degrees. In calculus, however, it is convenient to study trigonometry in a more

general setting and to measure angles differently.

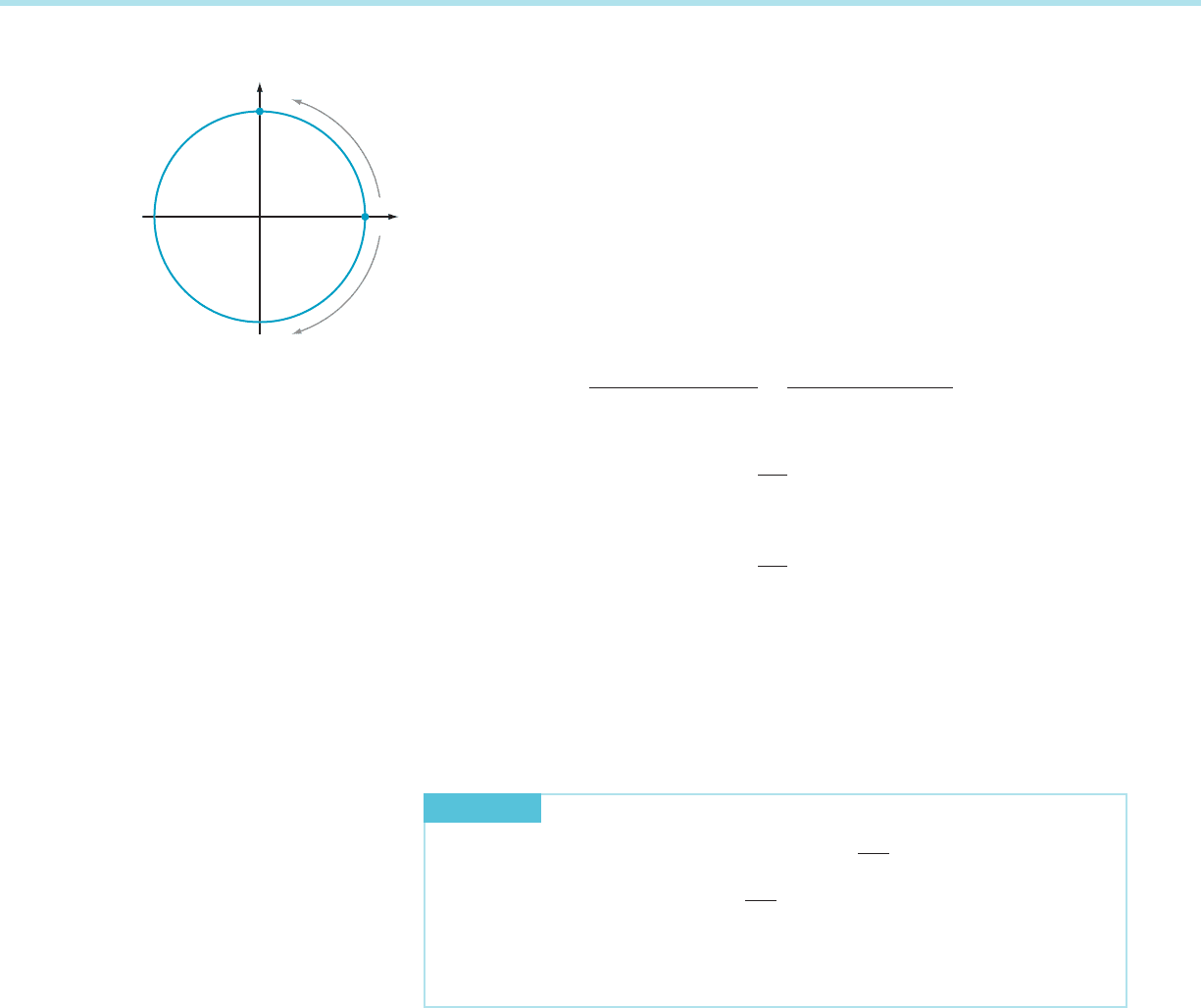
In calculus, we measure angles by rotation along the unit circle in the plane,

beginning at the positive x-axis. Counterclockwise rotation corresponds to positive

angles, and clockwise rotation corresponds to negative angles (see Figure 1). The

radian measure of an angle is deﬁned as the length of the arc of the unit circle that it

subtends with the positive x-axis (with an appropriate 1 or 2 sign).

In degree measure, one full rotation about the unit circle is 360



; in radian

measure, one full rotation about the circle is the circumference of the unit circle,

namely 2π. Let us use the symbol θ to denote an angle. The principle of pro-

portionality tells us that

degree measure of θ

360



radian measure of θ

2π

In other words,

radian measure of θ 5

180

ðdegree measure of θÞ

and

degree measure of θ 5

180

ðradian measure of θÞ:

Figure 2 shows several angles that include both the radian and degree measures.

This book always refers to radian measure for angles unless degrees are explicitly

speciﬁed. Doing so makes the calculus formulas simpler. Thus for example, if we

refer to “the angle 2π/3,” then it should be understood that this is in radian mea-

sure. Likewise, if we refer to “the angle 3,” it is also understood to be radian

measure. We sketch this last angle (see Figure 3) by noting that a full rotation is

2π 5 6.28 . . . , and 3 is a little less than half of that.

Sine and Cosine

Functions

DEFINITION

Let A 5 (1, 0) denote the point of intersection of the unit circle

with the positive x-axis. Let θ be any real number. A unique point P 5 (x, y)

on the unit circle is associated with θ by rotating

OA by θ radians. (Remember

that the rotation is counterclockwise for θ . 0 and clockwise for θ , 0.)

(See Figure 4.) The resulting radius

OA is called the terminal radius of θ, and P

is called the terminal point corresponding to θ. The number y is called the sine of

θ and is written sin (θ). The number x is called the cosine of θ and is written

cos (θ).

(0, 1)

(1, 0)

Positive

angles

Negative

les

m Figure 1 The unit circle

1.6 Trigonometry 65

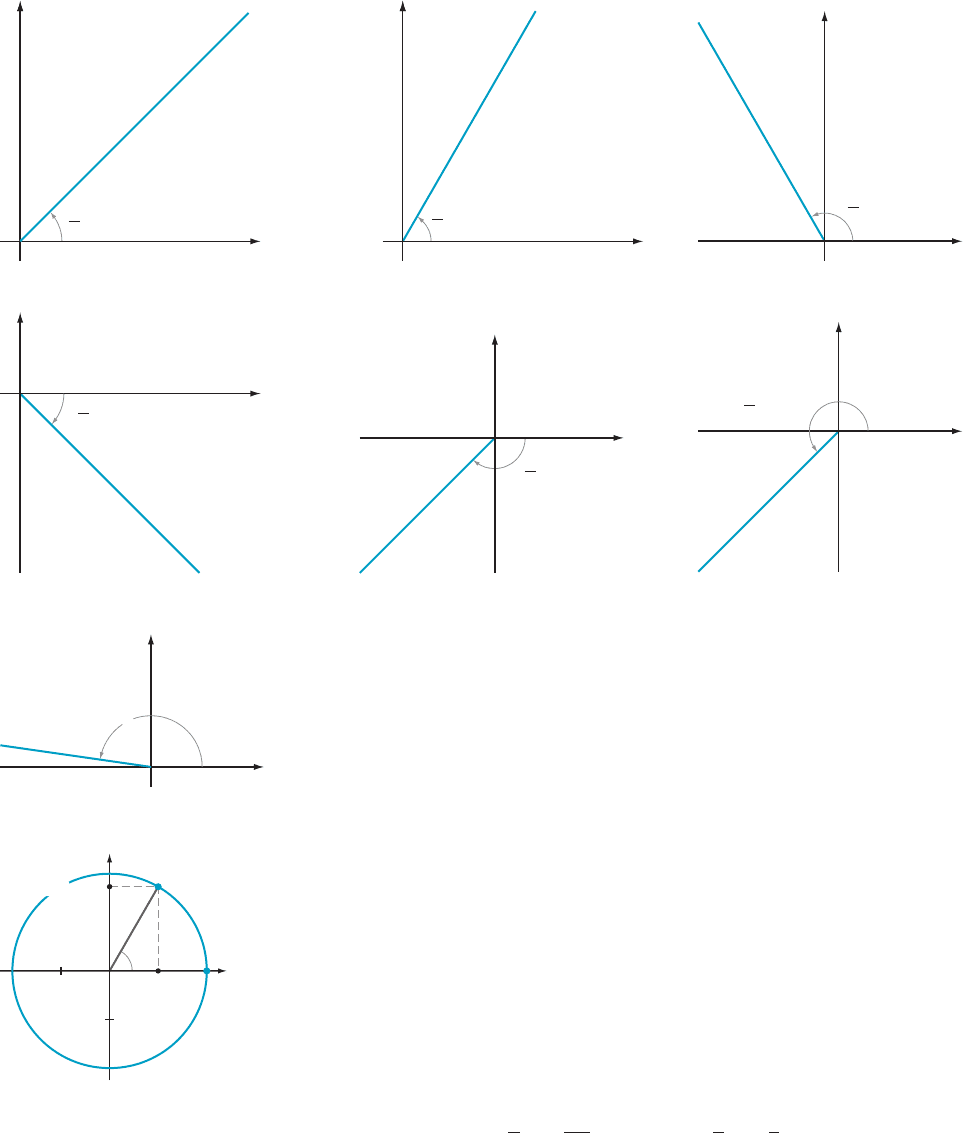
Because the point (cos (θ), sin (θ)) is on the unit circle, the following two fun-

damental properties are immediate:

ðsinðθÞÞ

1 ðcosðθÞÞ

5 1 for any θ in R; ð 1 :6:1Þ

and

21 # cosðθÞ # 1 and 21 # sinðθÞ # 1 for any θ in R:

It is common to write sin

(θ) to mean (sin (θ))

and cos

(θ) to mean (cos (θ))

This is consistent with the notation for functions described in Section 1.5. Indeed,

sine and cosine are both functions; each has domain equal to R and image equal to

[21, 1].

⁄ EX

AMPLE 1 Compute the sine and cosine of π/3

Solution We

sketch the terminal radius and associated triangle (see Figure 5). This

is a π/6 2 π/3 2 π/2 (30



2 60



2 90



) triangle with sides of ratio 1:

ﬃﬃﬃ

: 2. Thus the

side-length x of Figure 5 satisﬁes 1/x 5 2, or x 5 1/2. Likewise, the side-length y of

Figure 5 satisﬁes y/x 5

ﬃﬃﬃ

,ory 5

ﬃﬃﬃﬃﬃ

ﬃﬃﬃ

=2. It follows that

sin





ﬃﬃﬃ

and cos





: ¥

p  45



m Figure 2d

p  135



m Figure 2e

p  225

m Figure 2f

p  60

m Figure 2b

p  120

m Figure 2c

m Figure 3

A  (1, 0)

0.5

x  cos(u)

P  (x, y)

y  sin(u)

m Figure 4

p  45

m Figure 2a

66 Chapter

1 Basics

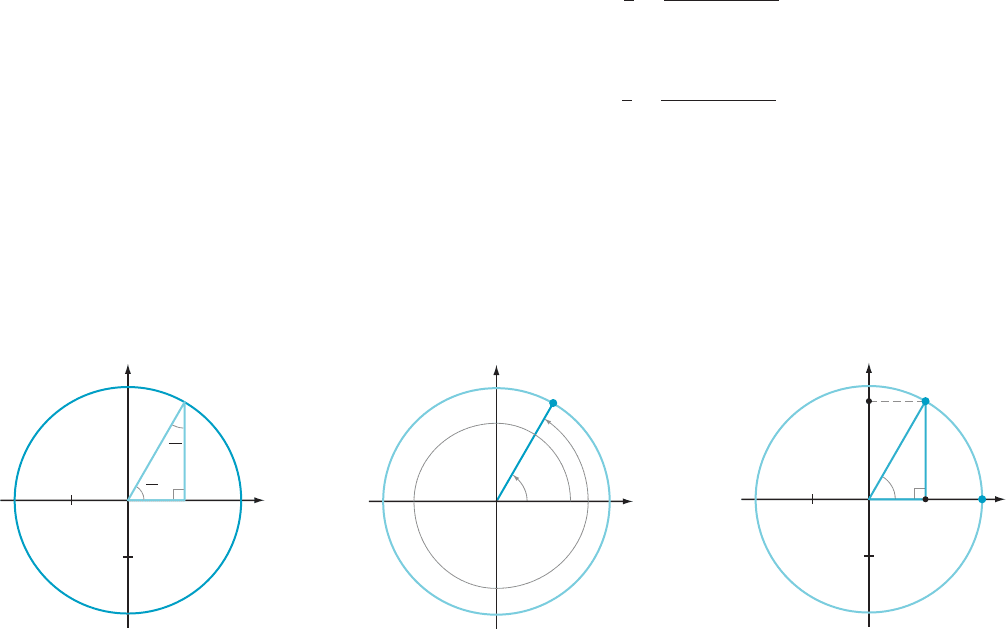
If θ is any number, then θ and θ 1 2π have the same terminal radius and the

same terminal point (adding 2π simply adds one more trip around the circle—see

Figure 6). As a result,

sinðθÞ5 sinðθ 1 2πÞ

and

cosðθÞ5 cosðθ 1 2πÞ:

We say that the sine and cosine functions have period 2π. In other words, the

functions repeat themsel ves every 2π units.

In practice, when we calculate the trigonometric functions of an angle θ,we

reduce it by multiples of 2π so that we can consider an equivalent angle θ

, called

the associated principal angle, satisfying 0 # θ

, 2π. For instance, 15π/2 has asso-

ciated principal angle 3π/2 (because 3π/2 5 15π/2 2 3 2π)and210π/3 has asso-

ciated principal angle 2π/3 because 2π/3 5210 π/3 1 2 2 π.

How does the concept of angle and sine and cosine presented here relate to the

classical notion using triangles? Any angle θ such that 0 # θ , π/2 has a right tri-

angle in the ﬁrst quadrant associated to it, with a vertex on the unit circle such that

the base is the segment connecting (0, 0) to (x, 0), and the height is the segment

connecting (x,0) to (x, y) (see Figure 7). Therefore

sinðθÞ5 y 5

opposite side

hypotenuse

and

cosðθÞ5 x 5

adjacent side

hypotenuse

Thus for angles θ between 0 and π/2, the new deﬁnition of sine and cosine using the

unit circle is equivalent to the classical deﬁnition using adjacent and opposite sides

and the hypotenuse. For other angles θ, the classical approach is to reduce to this

special case by subtracting multiples of π/2. The approach using the unit circle is

considerably clearer because it makes the signs of sine and cosine obvious.

0.5

P  (x, y)

m Figure 5

P  (x, y)

u  2p

m Figure 6

cos(u)

sin(u)

(0, y)

(x, 0)

0.5

(x, y)

(1, 0)

m Figure 7

1.6 Trigonometry 67

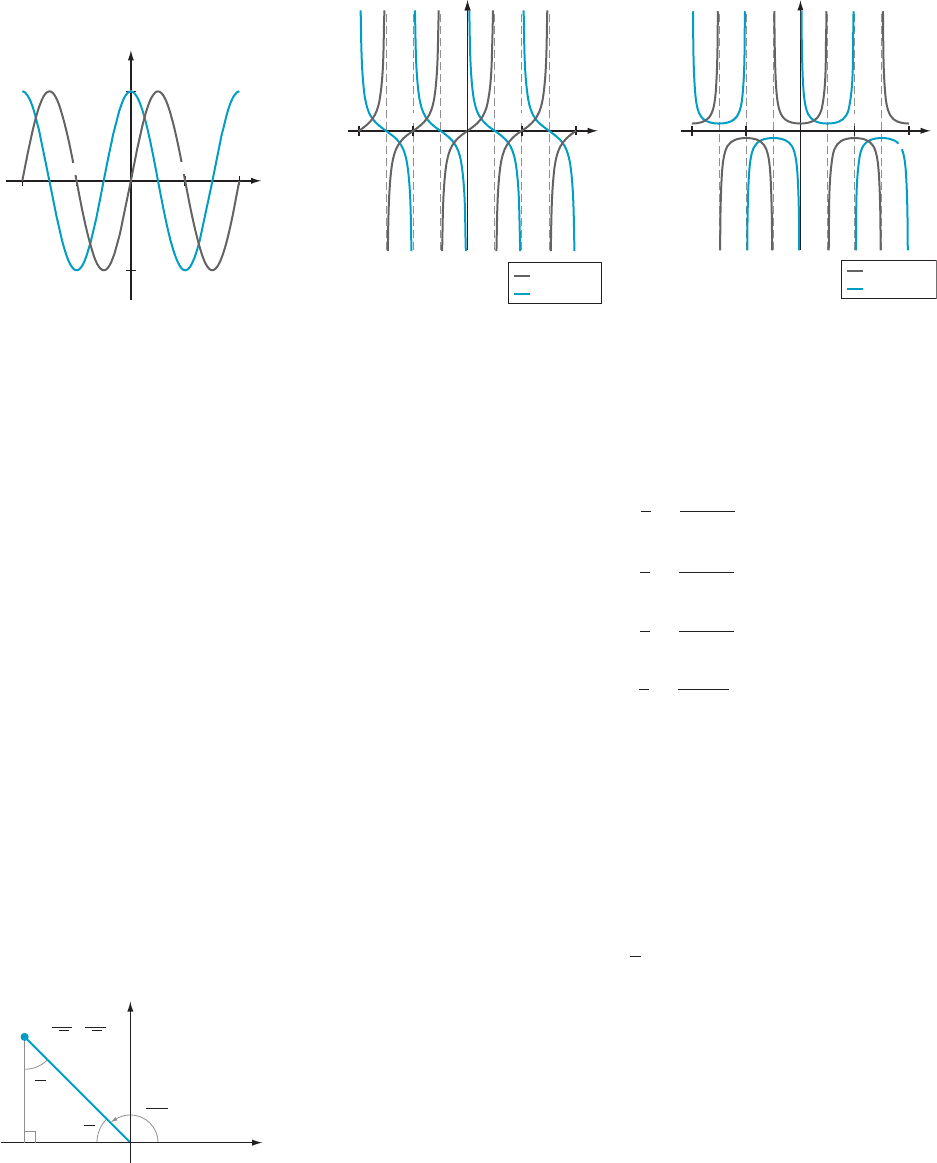
Other Trigonometric

Functions

In addition to sine and cosine, there are four other trigonometric functions—

tangent, cotangent, secant, and cosecant—deﬁned as follows:

tanðθÞ 5

sinðθÞ

cosðθÞ

cotðθÞ 5

cosðθÞ

sinðθÞ

secðθÞ 5

cosðθÞ

cscðθÞ 5

sinðθÞ

Whereas sine and cosine have the entire real line for their domain, tan (θ) and

sec (θ) are unde ﬁned at odd multiples of π/2 (because cosine is zero there). Also,

the functions cot (θ) and csc (θ) are undeﬁned at even multiples of π/2 (because sine

is zero there).

Figure 8 shows the graphs of the six trigonometric functions. Compare the

graph of the cosine and sine functions. We obtain the graph of y 5 cos (θ)by

shifting the graph of y 5 sin (θ)byπ/2 to the left. According to Theorem 1 from

Section 1.5, this means that

sin x 1



5 cosðxÞ:

This identity is a special case of the Addi tion Formula for the sine, which is given in

equation (1.6.4) in the next section.

⁄ EX

AMPLE 2 Compute all trigo nometric functions for the angle θ 5 11π/4.

Solution Because

the principal associated angle is 3π/4, we deal with that angle.

Figure 9 shows that the triangle associated to this angle is an isosceles right triangle

with hypotenuse 1. Therefore x 521=

ﬃﬃﬃ

and y 5 1 =

ﬃﬃﬃ

. It follows that

2p

1

sin(u)

cos(u)

pp

m Figure 8a

2␲

␪

2␲

␲␲

y  tan(␪)

y  cot(␪)

m Figure 8b

2␲

y  sec(␪)

y  csc(␪)

␪

2␲

␲

␲␲

m Figure 8c









m Figure 9

68 Chapter

1 Basics

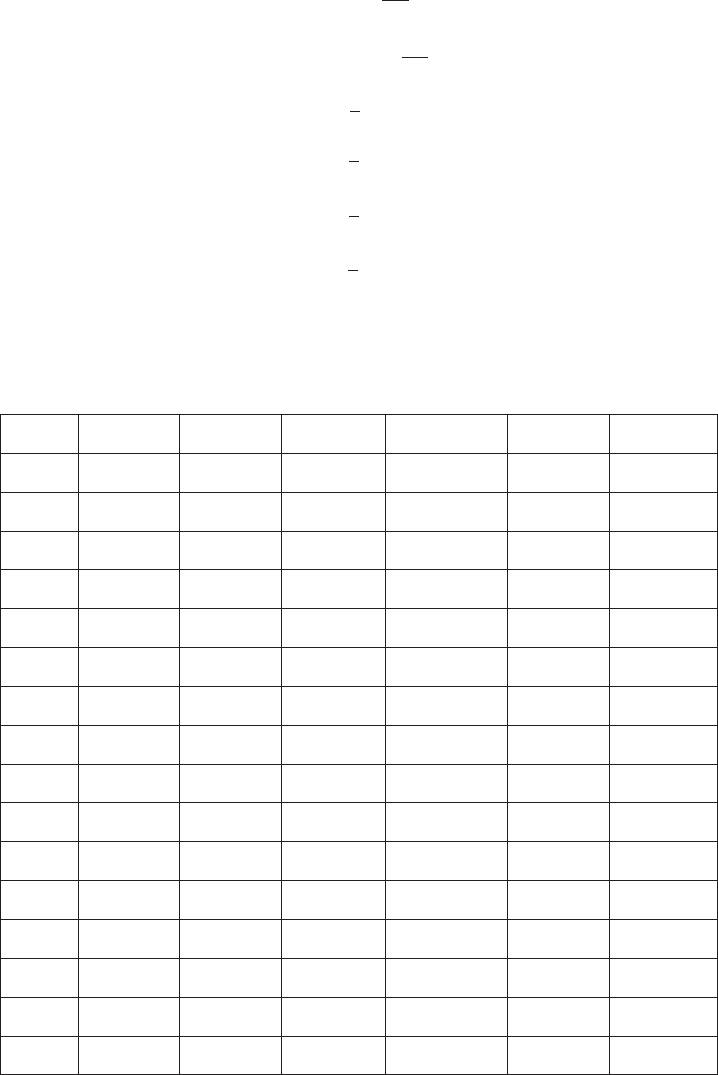
sinðθÞ 5 y 5

ﬃﬃﬃ

cosðθÞ 5 x 52

ﬃﬃﬃ

tanðθÞ 5

521

cotðθÞ 5

521

secðθÞ 5

ﬃﬃﬃ

cscðθÞ 5

ﬃﬃﬃ

: ¥

Similar calculations allow us to complete Table 1 for the values of the

trigonome

tric functions at the principal angles that are multiples of π/6 or π/4.

Angle Sine Cosine Tangent Cotangent Secant Cosecant

0 1 0 undef 1 undef

π=6 1/2

ﬃﬃﬃ

=21=

ﬃﬃﬃ

p ﬃﬃﬃ

ﬃﬃﬃ

π=4

ﬃﬃﬃ

=21 1

ﬃﬃﬃ

p ﬃﬃﬃ

π=3

ﬃﬃﬃ

=2 1/2

ﬃﬃﬃ

22=

ﬃﬃﬃ

π=2 1 0 undef 0 undef 1

2π=3

ﬃﬃﬃ

=2 21/2 2

ﬃﬃﬃ

2 1=

ﬃﬃﬃ

222=

ﬃﬃﬃ

3π/4

ﬃﬃﬃ

=2 2

ﬃﬃ

ﬃ

=2 21 21 2

ﬃﬃﬃ

p ﬃﬃﬃ

5π=6 1/2 2

ﬃﬃﬃ

=2 2 1=

ﬃﬃﬃ

2 2=

ﬃﬃﬃ

π 0 21 0 undef 21 undef

7π/6 21/2 2

ﬃﬃﬃ

=21=

ﬃﬃﬃ

p ﬃﬃﬃ

2 2=

ﬃﬃﬃ

5π/4 2

ﬃﬃﬃ

=2 2

ﬃﬃﬃ

=21 1 2

ﬃﬃﬃ

4π/3 2

ﬃﬃ

ﬃ

=2 21/2

ﬃﬃﬃ

22 2 2=

ﬃﬃﬃ

3π/2 21 0 undef 0 undef 21

5π=3 2

ﬃﬃﬃ

=2 1/2 2

ﬃﬃﬃ

2 1=

ﬃﬃﬃ

2 2 2=

ﬃﬃﬃ

7π/4 2

ﬃﬃﬃ

=2 21 2 1

ﬃﬃﬃ

11π/6 21/2

ﬃﬃﬃ

=2 2 1=

ﬃﬃﬃ

ﬃﬃ

ﬃ

Table 1

1.6 Trigonometry 69

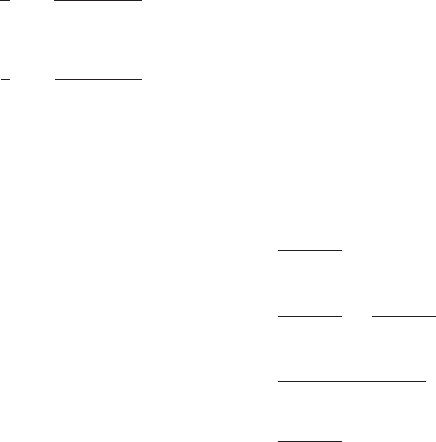
Trigonometric Identities The trigonometric functions satisfy many useful identities. In addition to equation

(1.6.1) already stated, we will need the following important formulas:

1 1 tan

ðθÞ5 sec

ðθÞð1:6:2Þ

1 1 cot

ðθÞ5 csc

ðθÞð1:6:3Þ

sinðθ 1 φÞ5 sinðθÞcosðφÞ1 cosðθÞsin ðφÞðAddition FormulaÞð1:6:4Þ

cosðθ 1 φÞ5 cosðθÞcosðφÞ2 sinðθÞ sinðφÞðAddition FormulaÞð1:6:5 Þ

sinðθ 2 φÞ5 sinð θÞ cosðφÞ2 cosðθÞsinðφÞðAddition FormulaÞð1:6:6 Þ

cosðθ 2 φÞ5 co

sðθÞcosð φÞ1 sinðθÞsinðφÞðAddition FormulaÞð1:6:7Þ

sinð2θÞ5 2sinðθÞcos ðθÞðDouble Angle FormulaÞð1:6:8Þ

cosð2θÞ5 cos

ðθÞ2 sin

ðθÞðDouble Angle FormulaÞð1:6:9Þ

sinð2 θÞ52 sinðθÞðSine is an odd functionÞð1:6:10Þ

cosð2θÞ5 cosðθÞðCosine is an even functionÞð1:6:11Þ

sin





1 2 cosðθÞ

ðHalf Angle FormulaÞð1:6:12Þ

cos





1 1 cosðθÞ

ðHalf Angle FormulaÞð1:6:13Þ

⁄ EX

AMPLE 3 Prove identity (1.6.2): 1 1 tan

ðθÞ5 sec

ðθÞ:

Solution Using

identity (1.6.1), we have

tan

ðθÞ1 1 5

sin

ðθÞ

cos

ðθÞ

1 1

sin

ðθÞ

cos

ðθÞ

cos

ðθÞ

cos

ðθÞ

sin

ðθÞ1 cos

ðθÞ

cos

ðθÞ

cos

ðθÞ

5 sec

ðθÞ: ¥

Identities (1.6.1)(1.6.13)

were known to the astronomer Hipparchus (ca. 180

125 BCE). There are many other trigonometric identities of a more specialized

nature.

70 Chapter 1 Basics

Modeling with

Trigonometric

Functions

Although the subject of trigonometry was invented by the ancient Greek astron-

omers for physical measurement, the trigonometric functions have proved to be

useful in many contexts. For example, because the sine function is cyclic with

period 2 π (i.e., the sine function repeats itself after 2π), it is often used to model

cyclic phenomena.

⁄ EX

AMPLE 4 The table shows the normal monthly mean temperatures of

St. Louis, Missouri, in degrees Fahrenheit.

Jan. Feb. March April May Jun e July Aug. Sept. Oct. Nov. Dec.

34 43 56 66 75 79 77 70 58 45 34

Model the mean temperature (T )

as a function of time (t) by using the equation

TðtÞ5 b 1 A sinðω  t 1 φÞð1:6:14Þ

for suitable constants b, A, ω, and φ. Use one month as the unit of time. Locate the

origin of the time axis so that t 5 0 corresponds to January 1, and t 5 12 corresponds

to December 31. Assume that, for each month, the actual temperature in the

middle of the month is equal to the mean temperature for that month. That is,

construct your model so that T(1/2) 5 29, T(3/2) 5 34, T(5/2) 5 43, and so on.

Solution First

observe that

sin



2π



1 φ



5 sinðωt

1 2π 1 φÞ5 sin ðωt

1 φÞ:

On setting t 5 t

2π

in formula (1.6.14), we see that, for every value of t



2π



5 b 1 A sin



ω 



2π



1 φ



5 b 1 A sinðω  t

1 φÞ5 Tðt

Þ:

In other words, the function T repeats itself after 2π/ω. This duration is called the

period of T. Bec ause the period of weather is 12 when measured in months, we set

2π/ω 5 12, or ω 5 π/6. Thus T(t) 5 b 1 A sin (πt/6 1 φ). To identify the values of A

and b, we note that b2A # T(t) # b 1 A (because 21 # sin(πt/6 1 φ) # 1). Because

the least mean temperature is 29, and the greatest mean temperature is 79, we set

b2A 5 29, and b 1 A 5 79. Solving these two equations simultaneously, we obtain

b 5 54, and A 5 25. Thus

TðtÞ5 54 1 25 sin



t 1 φ



To ﬁnd the value of φ, notice that the maximum value of sin(πt/6 1 φ) occurs when

the sine takes on its maximum value 1. That is, the expression sin(πt/6 1 φ)is

maximized when πt/6 1 φ 5 π/2. Therefore the function T(t) is maximized when

πt/6 1 φ 5 π/2. Looking at the table, we make the reasonable assumption that

this maximum is 79 and occurs in the middle of July, when t 5 13/2. Thus we set

π (13/2)/ 6 1 φ 5 π/2. This gives φ 527π/12. Our model is

TðtÞ5 54 1 25 sin



t 2

7π



1.6 Trigonometry 71

Figure 10 shows how well this model ﬁts the measured data. ¥

QUICK QUIZ

1. What is the domain of the sine function?

2. What is the image of the cosine function?

3. Which trigonometric functions are even? Odd?

4. Simplify sin (2θ) / sin (θ).

Answers

1. R 2.

[21, 1] 3. even: cos and sec; odd: sin, tan, cot, csc, 4. 2 cos(θ)

10 23456789101112

T(t)  54  25 sin



t 



m Figure 10

EXERCISES

Problems for Practice

c In Exercises 14, calculate each of the six trigonometric

functions at angle θ without using a calculator. b

1. θ 5 π/6

2. θ 5 π/4

3. θ 5 2π/3

4. θ 5 4π/3

c In Exercises 514, calculate the given expression without

using

a calculator. b

5. sin

(π/3) sin (π/6)

6. cos (0)2cos (π)

7. cos (π/6) 1 cos (π/3)

8. sin (π/4) cos (π/4)

9. tan (π/3) / tan (π/6)

10. cos (2π/3) csc (2π/3)

11. sin (π sin (π/6))

12. sec (2π/3)

csc (2π/2)

13. sin (19π/2)

cos (33π)

14. 4 tan (π/4) 2 sin (17π/2)

c In Exercises 1520, θ is

a number between 0 and π/2.

Calculate the unevaluated trigonometric function from the

given information. b

15. cos

(θ); sin (θ) 5 1/3

16. tan (θ); cos (θ) 5 3/5

17. sin (2θ); cos (θ) 5 4/5

18. sin (θ/2); cos (θ) 5 3/7

19. cos (θ/2); sin (θ) 5 5/13

20. cos (θ 1 π); cos (θ) 5 0.1

c In Exercises 2124, state which of the six trigonometric

functions

are positive when evaluated at θ in the indicated

interval. b

21. θ A (0, π/2)

22. θ A (π/2, π)

23. θ A (π,3π/2)

24. θ A (3π/2,

2π)

c In Exercises 2528, graph the function. b

25. f (t) 5 sin

(2t), 22π # t # 2π

26. f (t) 5 cos (t/2), 22π # t # 2π

72 Chapter 1 Basics

27. f (t) 5 sin (t2π/6), 0 # t # 2π

28. f (t) 5 cos (2t 1 π/3), 0 # t # 2π

c In Exercises 2931, use the cosine and sine functions to

give

a parameterization of the unit circle such that the domain

of parameterization is [0, 2π) and the additional requirements

are satisﬁed. b

29. The

initial point is (1, 0), and the circle is traced coun-

terclockwise as the parameter value increases.

30. The initial point is (0, 1), and the circle is traced coun-

terclockwise as the parameter value increases.

31. The initial point is (0, 1), and the circle is traced clockwise

as the parameter value increases.

Further Theory and Practice

32. For each θ in f0, π /6, π/4, π/3, π/2g, ﬁnd an integer value of

n such that sinðθÞ5

ﬃﬃﬃ

=2 (The pattern found in this

exercise is sometimes used as a memory aid.)

33. The length s(r, θ) of an arc of a circle that subtends a

central angle of radian measure θ is proportional to the

radius r of the circle and to θ. What is s ( r , θ)?

34. For a circle of radius r, the area A(r, θ) of a sector with

central angle measuring θ radians is jointly proportional

to θ and to r

. What is A(r, θ)?

35. The equations sin (2θ) 5 sin (θ) cos (θ) and sin (2θ) 5

2 sin (θ) cos (θ) are fundamentally different. Explain why.

36. Find constants A and B such that

sinð3θÞ5 A sin ðθÞ2 B sin

ðθÞ

for every θ.

c In Exercises 3744, use one or more of the basic trigo-

nometric

identities to derive the given identity. b

37. tanðθ 1 φÞ5

tanðθÞ1 tanðφÞ

1 2 tanðθÞtanðφ Þ

38. sinðθÞsinðφÞ5

cosðθ 2 φÞ2 cosðθ 1 φÞ

39. cosðθÞcosðφÞ5

cosðθ 2 φÞ1 cosðθ 1 φÞ

40. sinðθÞcosðφÞ5

sinðθ 1 φÞ1 sinðθ 2 φÞ

41. sinðθÞ5 cos



2 θ



42. sin (θ 1 π) 52sin (θ)

43. cos (θ 1 π) 52cos (θ)

44. tan (θ 1 π) 5 tan (θ)

45. Use the identity π/3 1 π/4 5 7π/12 to calculate the six

trigonometric functions at 7π/12.

46. Use the Half Angle Formulas to evaluate the six trigo-

nometric functions at π/8.

c In each of Exercises 4750, derive the given identity by

using

the identities in Exercises 3840. b

47. sinðθÞ1 sin ðφÞ5 2

sinð

θ 1 φ

Þcosð

θ 2 φ

48. sinðθÞ2 sin ðφÞ5 2cosð

θ 1 φ

Þsin ð

θ 2 φ

49. cosðθÞ1 cosðφÞ5 2cos ð

θ 1 φ

Þcos ð

θ 2 φ

50. cosðθÞ2 cosðφÞ522sinð

θ 1 φ

Þsinð

θ 2 φ

51. Suppose that A and B are constants. Use the Addition

Formula for the sine to ﬁnd an amplitude C and a phase

shift φ (both in terms of A and B) such that

Acos ðθÞ1 BsinðθÞ5 C sinðθ 1 φÞ

for every θ.

52. Let y 5 mx 1 b be the equation of a nonhorizontal, non-

vertical line. Such a line intersects the x-axis making an

angle φ with the positive x-axis that has radian measure

between 0 and π. What is the relationship between m and

φ? Can this relationship, suitably interpreted, be extended

to vertical or horizontal lines? Why is φ independent of b?

53. The angle of elevation of a point above the earth is the

acute angle between the horizontal and the line of sight.

Suppose two points on the earth’s surface have distance ‘

between them. Line ‘ is small enough for us to assume

that the earth is ﬂat between the two points. Suppose that

θ and φ are the angles of elevation of a mountain peak

relative to these two points (see Figure 11). Show that the

height h of the mountain is given by

h 5

‘

jcotð θÞ2 cotðφÞj

c Suppose that a and b are

positive constants. In Exercises

5457, identify the curve that is parameterized by the equa-

tions.

In each case, use a trigonometric identity to eliminate

the parameter. (It may help to consider the special case

a 5 b 5 1 ﬁrst.) b

54. x 5 a cos

(θ), y 5 b sin (θ), θ A [0, 2π]

55. x 5 a cos

(θ), y 5 b sin

(θ), θ A [0, π]

56. x 5 a sec (θ), y 5 b tan (θ), θ A [0, π/2)

57. x 5 a tan (θ), y 5 b cot(θ), θ A (0, π/2)

ᐉ

m Figure 11

1.6 Trigonometry 73

58. Suppose that h and k are constants and that a and b are

positive constants. Parameterize the ellipse with center

(h, k) and semi-axes a and b parallel to the x-axis and

y-axis.

c A function f is

said to have period p if there is a smallest

positive number p such that f (x 1 p) 5 f (x) for all x in the

domain of f. In Exercises 5963, ﬁnd the period of the

function

deﬁned by the given expression. b

59. sinðx 1

ﬃﬃ

ﬃ

60. cos (2πx)

61. tan (x)

62. sin (x) 1 tan (x)

63. tan (2x) 1 sin (3x)

64. The lowest monthly normal temperature of Philadelphia

is 31



F and occurs in January. The highest monthly nor-

mal temperature of Philadelphia is 77



F and occurs in

July. Find a model of temperature T as a function of time

t that has the form T(t) 5 b 1 A sin (ωt 1 φ).

65. The lowest monthly normal temperature of Nome is 4



and occurs at the end of December (t 5 12). The highest

monthly normal temperature of Nome is 51



F and occurs

at the beginning of July (t 5 6). Find a model of tem-

perature T as a function of time t that has the form T(t) 5

b 1 A sin (ωt 1 φ).

66. The number of visitors to a tourist destination is seasonal.

However, the long-term trend at this particular destina-

tion is down. A model for the number of tourists y as a

function of time t measured in years is

yðtÞ5 5  10

2 1 cosð2πtÞ

1 1 t

1=4

Here t 5 0 corresponds to a time at which there were

150, 000 tourists. Is y a periodic function of t? (Refer to

the instructions for Exercise 59 for the deﬁnition of

“period.”) Sketch the graph of y as a function of t for

0 # t # 4. From the sketch, y has local maxima at

t 5 1, 2, 3, and so on. Deﬁne in your own words what the

statement “a local maximum of y occurs at t

” means.

67. A polygon is regular if all sides have equal length. For

example, an equilateral triangle is a regular 3-gon (tri-

angle) and a square is a regular 4-gon (quadrilateral). A

polygon is said to be inscribed in a circle if all of its

vertices lie on the circle.

a. Show that the perimeter p(n, r) of a regular n-gon

inscribed in a circle of radius r is

pðn; rÞ5 2rn sin





b. Show that the area A( n,r) of a regular n-gon inscribed

in a circle of radius r is

Aðn; rÞ5

n sin



2π



Calculator/Computer Exercises

68. Graph y 5 12cos (2x) and y 5 sin (x) in [0.2, 1]3[0, 1.5].

Successively zoom in to the point of intersection to ﬁnd a

value x

A (0.2, 1) that satisﬁes 1 2 cos (2 x

) 5 sin (x

Give x

to three decimal places. What is sin (x

) to three

decimal places? Use a trigonometric identity to ﬁnd the

exact value of sin (x

69. Calculate the values of the sequence a

5 n sin (1/n) for

1 # n # 15. Now calculate a

for larger values of n by

setting n 5 10

for 1 # k # 6. There is a number ‘, which is

called the limit of a

, such that ‘ 2 a

decreases to 0 as n

increases to inﬁnity. What is ‘ Now plot f (x) 5 sin (x)/x

for 0 # x # 1. Explain how the limiting behavior of a

can

be determined from this graph.

70. Calculate the values of the sequence a

5 n

(1 2 cos (1/n))

for 1 # n # 15. Now calculate a

for larger values of n by

setting n 5 10

for 1 # k # 4. There is a number ‘, which

is called the limit of a

,suchthat‘ 2 a

decreases to

0asn increases to inﬁnity. What is ‘? Now plot f (x) 5

(12cos (x)) / x

for 0 , x # 1. Explain how the limiting

behavior of a

can be determined from this graph.

71. Graph f (x) 5 90x 1 cos (x)intheviewingwindows

[210, 10] 3 [21000, 1000] and [20.0001, 0.0001] 3 [0.5, 1.5].

Explain why the graph of f appears to be a straight line in

each of these windows. Which straight lines do these

graphs appear to coincide with? Sketch the graph of the

function f in a way that better displays its behavior.

72. In later chapters, we will investigate the approximation of

complicated functions by simpler ones. For instance, the

function x/x is a good approximation to the function

x/sin (x) cos (x

) for jxj sufﬁciently small. Use a graph-

ing utility to ﬁnd an interval on which x approximates

sin (x) cos (x

) with an absolute error of at most 0.01.

73. The monthly normal temperatures in degrees Fahrenheit

for Raleigh, North Carolina, are 40, 42, 49, 59, 67, 74, 78,

77, 71, 60, 50, and 42 (starting with January). Plot these

temperatures. Find and plot a continuous model.

c Cosine waves are

functions of the form x/A cos (νx 1 φ)

where A is the amplitude of the wave, ν the frequency, and φ

the phase shift. The physical superposition of two waves is

obtained mathematically by adding the two wave functions.

Exercises 7476 concern the superposition of cosine waves.

The

identities from Exercises 49 and 50 are particularly useful

in this context. b

74. For φ 5 0, π/3,

2π/3, and 3π/2, graph the superposition

x/cos (2x) 1 cos (2x 1 φ), 0 # x # 2π. Each of these four

curves is the graph of a wave of the form x/A cos

(2x 1 θ) for some amplitude A and phase shift θ, each

depending on φ. Use your graph to determine A and θ

when φ 5 2π/3. Use the identity from Exercise 39 to

obtain a formula for A and θ. Calculate the magnitude of

the superposed wave at x 5 2 for the four given values

74 Chapter 1 Basics