Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

input values, and the image is the set of output values. The range is a set that

contains every value in the image but may also contain some values that the function

does not actually assume. We can think of the range as the set of possible output

values of the function. For example, if a teacher who has 60 students in a class

enters exam grades in a column of a spreadsheet, then the grade recorded in the i

row is a function f of i. If the grades are integers between 0 and 100, then it is

convenient to take f0, 1, 2, 3, . . . , 100g to be the range of f and write f : f1, 2,

3, . . . , 60g- f0, 1, 2, 3, . . . , 100g. The image of f consists of the grades that were

actually attained by students. Because there are no more than 60 such grades, the

chosen range is certainly larger than the image. Yet we easily indi cated the range,

whereas we would have found it tiresome to write out all the values of the image.

Examples of Functions

of a Real Variable

The domains and ranges of the functions encountered in calculus are usually sets of

real numbers; in fact, these sets will often consist of one or more intervals in R.A

function with a domain that is a set of real numbers is a function of a real variable .

A function with a range that is a set of real numbers is a real-valued function. Often,

we use arrow notation, x / f (x) (the symbol/is read as “is mapped to”). If we

refer to a function f by giving a formula for f (x) without specifying the domain,

then the domain of f is understood to be the largest set of real values x for which

f (x) makes sense as a real number. If the range of a real-valued function f is not

explicitly speciﬁed, then we understand the range to be the entire real line R. The

theorems of calculus often enable us to determine the image of f.

⁄ EX

AMPLE 1 Let FðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

9 2 x

. What is the domain of F?

Solution For F(x)

to make sense as a real number, the inequality

9 2 x

$ 0

must be satisﬁed. Therefore x

# 9, or 23 # x # 3. In summary, the domain of F is

the interval [23, 3].

Example 1 illustrates one of the most common considerations in determining

the domain of a function: The argument of an even root such as

ﬃp

ﬃ

must be

nonnegative. The example that follows illustrates another situation that must often

be considered: The de nominator of a fraction may not be zero.

⁄ EX

AMPLE 2 Let G(x) 5 x

1 2x 1 4 and H(x) 5 (x

2 8)/(x 2 2). Show that

G(x) 5 H(x) for every x 6¼2. Are G and H the same function?

Solution The

identity

2 8 5 ðx

1 2x 1 4Þðx 2 2Þð1:4:1Þ

is true for every x, as we can verify by expanding the right side and combining

terms. However, because division by 0 is not deﬁned, we can divid e each side of

(1.4.1) by x 2 2 only when x 6¼2. Thus we have

HðxÞ5

2 8

x 2 2

ðx

1 2x 1 4Þðx 2 2Þ

ðx 2 2Þ

5 x

1 2x 1 4 5 GðxÞ for x 6¼ 2:

The domain D

of G is the largest set of real numbers for which the expression

1 2x 1 4 makes sense. Therefor e D

5 R. The domain D

of H is the largest set

1.4 Functions and Their Graphs 35

of real numbers for which the expression (x

28)/(x22) makes sense. We must

exclude x 5 2 because division by 0 is undeﬁned. Therefore D

5 fx 2 R : x 6¼ 2g.

We conclude that G and H are not the same function: they have different

domains.

INSIGHT

Suppose S

is a set that consists of some but not all points of a set S. Given

a function G deﬁned on S, we can create a function on the subset S

by assigning the

output value G(x) to the input value xAS

. This function is called the restriction of G to

. The notation Gj

is sometimes used to denote the restriction of G to S

. In Example 2,

the domain S of G equals R, the subset S

of S is fx 2 R : x 6¼ 2g, and H is the restriction

of G to S

Piecewise-Deﬁned

Functions

A function is often described by different rules over different subintervals of its

domain. Such a function is said to be a piecewise-deﬁned or multicase function.

The absolute value function x / jxj is a familiar multicase function that will

often be used in this text. It can be written as

x if x $ 0

2x if x , 0



Another example of a piecewise-deﬁned function that occurs frequently is the

signum,orsign, function:

signumðxÞ5

1ifx . 0

0ifx 5 0

21ifx , 0

The next example illustrates that multicase functions are often encountered in

everyday life.

⁄ EX

AMPLE 3 Schedule X from the 2008 U.S. income tax Form 1040 is

reproduced here. This form helps determine the income tax T(x) of a single ﬁler

with taxable income x .

Over But not over The tax is Of the amount over

$8025 10% $0

$8025 $32550 $802.50 1 15% $8025

$32550 $78850 $4481.25 1 25% $32550

$78850 $164550 $16056.25 1 28% $78850

$164550 $357700 $40052.25 1 33% $164550

$357700 $103791.75 1 35% $357700

Write T using

mathematical notation.

Solution The

function T is deﬁned for all positive values of x, but there are six

different cases. We use the following notation:

36 Chapter 1 Basics

TðxÞ5

0:10x if 0 , x # 8025

802:50 1 0:15ðx 2 8025Þ if 8025 , x # 32550

4481:25 1 0:25ðx 2 32550Þ if 3255 0 , x # 78850

16056:25 1 0:28ðx 2 78850Þ if 78850 , x # 164550

40052:25 1 0:33ðx 2 164550Þ if 164550 , x # 357700

103791:75 1 0 :35ðx 2 357700Þ if 357700 , x

For

a given value of x, there are two steps used to determine T(x). First, we must

determine the interval in which the value x lies. Second, we must apply the formula

that corresponds to that interval. For example, a single ﬁler with taxable income of

$30, 000 would observe that x 5 30000 lies in (8025, 32550] and would compute his

tax to be

Tð30000Þ5 802:50 1 0 :15ð30000 2 8025Þ5 $4098:80: ¥

Graphs of Functions In calculus, it is often useful to represent functions visually. Pictures, or graphs, can

help us think about functions. For now, we will only graph functions with domai ns

and ranges that are subsets of the real numbers. These real-valued functions of a

real variable are graphed in the xy-plane. The elements of a function’s domain are

thought of as points of the x-axis. A function’s values are measured on the y-axis.

DEFINITION

The graph of f is the set of all points (x, y) in the xy-plane for

which x is in the domain of f and y 5 f (x). Thus if f is a real-valued function that

is deﬁned on a set S of real numbers, then the graph of f is the curve f(x , y):

x A S, y 5 f (x)g.

The graphs of some basic functions are shown in Figure 1. If a number x

is not

in the domain of a function f, then there is no point of the form (x

, y) that lies on

the graph of f. In other words, the vertical line x 5 x

does not intersect the graph of

f when x

is outside the domain of f.Ifx

is in the domain of f, then there is one and

only one point of the form (x

, y) that lies on the g raph of f—namely, the uniqu e

point (x

, y

) with y

5 f (x

INSIGHT

These considerations lead to the Vertical Line Test: If every vertical

line drawn through a curve intersects that curve only once, then the curve is the graph

of a function. If there is a vertical line that intersects the curve in more than one

point, then the curve is not the graph of a function.

⁄ EXAMPLE 4 Is the graph of the equation x

1 y

5 13 the graph of a

function?

Solution The

graph of x

1 y

5 13 is the circle shown in Figure 2. Observe that

there are many vertical lines that intersect the graph in more than one point. It

takes only one such line to demonstrate that the curve is not the graph of a

1.4 Functions and Their Graphs 37

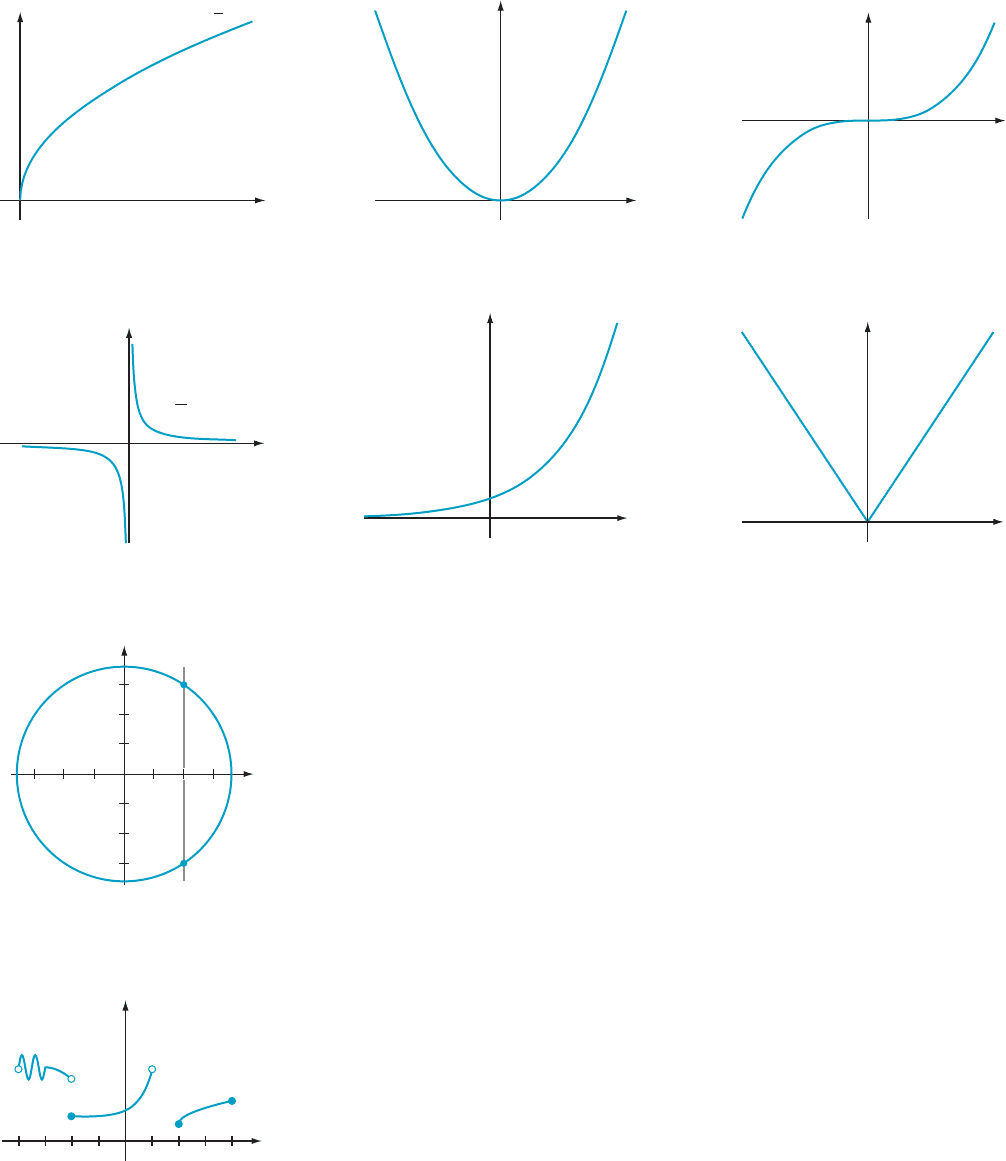
function. Figure 2 illustrates this idea with the vertical line x 5 2, for which there

are two y values, y 5 3 and y 523, such that (x, y) is on the given circle.

⁄ EXAMPLE 5 Is the curve in Figure 3 the graph of a function?

Solution For

each x that lies in either the open interval (28, 2) or the closed

interval [4, 8], there is only one corres ponding y value. Thus the curve passes the

Vertical Line Test and is the graph of a function x / f (x) (even though we do not

know a formula for f (x)). The domain of f is (28, 2),[4, 8].

Chapter 4 explains some techniques for graphing functions. For now, it is a

good idea to learn to recognize and sketch the graphs of basic functions (such as

those plotted in Figure 1) and to use a graphing calculator or computer for more

complicated functions. When we sketch a graph by hand, we can easily highlight

important features (such as isolated points missing from the domain) and note-

worthy details (such as intercepts). For instance, the function H from Example 2

is graphed in Figure 4. An open dot indicates that the number 2 is not in the

domain of H.

⁄ EX

AMPLE 6 Graph the signum function, which is deﬁned in the preceding

subsection.

Solution The

part of the graph of signum to the left of x 5 0 lies on the horizontal

line y 521. The part to the right of x 5 0 lies on the horizontal line y 5 1. A closed



y ⫽

m Figure 1a

y  x

m Figure 1b

y  x

m Figure 1c

y 

m Figure 1d

y  2

m Figure 1e

y  x

m Figure 1f

(2,3)

(2,3)

x  2

1

3

 y

 13

m Figure 2

42868 4 26

m Figure 3

38 Chapter

1 Basics

dot indicates that (0, 0) is on the graph of signum. Because the points (0, 21) and

(0, 1) are not on the graph of signum, we use open dots (see Figure 5).

⁄ EXAMPLE 7 One popular graphing calculator uses the rectangle [210,

10] 3 [210, 10] as its default viewing window. Explain why no parts of the graphs of

f ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 x 2 132

and gðxÞ5 ð2x

1 100Þ=ðx

1 2x 1 2Þ appear in this viewing

window.

Solution The

function f may be written as

f ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 x 2 132

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ðx 1 11 Þðx 2 12Þ

For x to be in the domain of f, the product (x 1 11)(x 2 12) must be nonnegative.

Therefore the factors x 1 11 and x 2 12 must have the same sign. This happens only

for x #211 (both facto rs nonpositive) and for x $ 12 (both factors nonnegative).

No part of the graph of f will appear in any viewing window of the form [210, 10] 3

min

, y

max

] because [210, 10] is not in the domain of f.

The problem with the graph of g is different. By completing the square in the

denominator, we see that g(x) 5 (2x

1 100)/((x 1 1)

1 1). The denominator is

greater than or equal to 1, hence it is never 0. The domain of g is, therefore, the set

of all real numbers. In particular, [210, 10] is in the domain of g, and we can be sure

that some viewing rectangle of the form [210, 10] 3 [ y

min

, y

max

] will contai n part of

the graph of g. Indeed, Figure 6 shows the graph of g in the viewing window

[210, 10] 3 [0, 250]. We see that g(x) . 10 for every value of x in [210, 10]. In other

words, the rectangle [210, 10] 3 [210, 10] lies entirely below the graph of g.

Sequences A function f with a domain that is the set Z

of positive integers is called an inﬁnite

sequence. In general, a function f is a sequence if its domain is a ﬁnite or inﬁni te set

of consecutive integers. We can write a sequence f by listing its values:

f ð1Þ; f ð2Þ; f ð3Þ;::: :

Thus a sequence f can be thought of as a list, with f (1) being the ﬁrst element of the

list, f (2) the second element, and so on. It is common to abandon the function

notation altogether and write the sequence as

; f

;:::;

or sometimes as ff

n51

,orevenasff

g. We refer to f

as the n

term of the

sequence f. Occasionally, it is useful to begin a sequence with an index different

from 1. An example is f3n 2 5g

n54

, which denotes the sequence 7, 10, 13, 16, . . . .

3215 4 3 2 1

H(x) 

 8

x  2

m Figure 4

1

424 2

m Figure 5 y 5 signum(x)

250

200

150

510510

y 

 100

 2x  2

y  10

m Figure 6

1.4 Functions and Their Graphs 39

⁄ EXAMPLE 8 For n 5 1, 2, 3, . . . let f

be the product of the positive inte-

gers less than or equal to n. List the ﬁrst six terms of ff

n51

Solution We

calculate f

5 1, f

5 2 1 5 2, f

5 3 2 1 5 6, f

5 4 3 2 1 5 24,

5 5 4 3 2 1 5 120, and f

5 6 5 4 3 2 1 5 720. ¥

INSIGHT

The numbers of Example 8 are known as factorials. They are important in

many ﬁelds of mathematics and they arise in calculus as well. It is common to write n!

(read n factorial) for f

. Thus n! 5 n (n 2 1) 3 2 1 for n 5 1, 2, 3, . . . . We also deﬁne

0! to be 1. That is, 0! 5 1.

⁄ EXAMPLE 9 Use the decimal expansion of π to deﬁne a sequence of

rational numbers fq

g that become progressively closer to π.

Solution We

can deﬁne such a sequence fq

g by q

5 3.1, q

5 3.14, q

5 3.141,

5 3.1415, q

5 3.14159, and so on. Thus

5 the first ðn 1 1Þ digits of the decimal expansion of π:

This is not a constructive deﬁnition because no method of computing the decimal

expansion of π has been given. Constructive sequences are given in the Exercises 57

and 58.

A sequence fs

g is inductively (or recursively) deﬁned if s

n 1 1

is deﬁned in

terms of some or all of its predecessors s

, ...,s

. In this case, we must specify (or

initialize) some of the ﬁrst few values of the sequence fs

⁄ EX

AMPLE 10 The Fibonacc i sequence f

is deﬁned by f

n12

5 f

n11

1 f

for

n $ 1. The values f

and f

are both initialized to be 1. What is f

Solution We

calculate:

5 f

1 f

5 1 1 1 5 2

5 f

1 f

5 2 1 1 5 3

5 f

1 f

5 3 1 2 5 5

5 f

1 f

5 5 1 3 5 8

5 f

1 f

5 8 1 5 5 13 ¥

Functions from Data In practice, many functional relationships are not initially discovered in the form of

mathematical expressions. For example, suppose that several observations or mea-

surements of two variables x and y are made and that y depends on x by means of an

undetermined function f. One way to ﬁnd an expression for f (x) is to plot a sequence

f(x

, y

)g of the observed values. The result is known as a scatter plot,orascatter

diagram. Comparison of the scatter plot with known graphs can suggest a suitable

formula for f. This formula is then said to be a mathematical model of the

observations.

⁄ EX

AMPLE 11 In 1929, the American astronomer Edwin Hubble pre-

sented evidence that indicates the expansion of the universe. Hubble measured the

distances and recession velocities of several galaxies relative to a ﬁxed galaxy.

40 Chapter 1 Basics

(Recession velocity is the speed at which two galaxies move away from each other.)

Some of Hubble’s data is tabulated here.

Virgo Pegasus Perseus Ursa

Major

Leo Gemini Bootes Hydra Coma

Berenices

d 22 68 108 255 315 405 685 1100 137

υ 0.75 2.4 3.2 9.3 12.0 14.4 24.5 38.0 ?

In the table, d repres

ents distance in millions of light years (here a light year is the

distance that light will travel in one year), an d υ represents velocity in thousands

of miles pe r second. Find a model for υ as a function of d. What is the recession

velocity of Coma Berenices?

Solution Figure

7 shows a plot of the tabulated data. Because d is the independent

variable and υ the dependent variable, we refer to the horizontal axis as the d-axis,

the vertical axis as the υ-axis, and the plane they determ ine as the dυ-plane.

Because the plotted points lie near a line that passes through the origin of the

dυ-plane, the mod el we seek has the equation υ 5 H d where H denotes the slope

of the line. The calculated values needed for the slope of the regression line

through the origin are recorded in the following table:

d υ d υ d

22 0.75 16.5 484

68 2.4 163.2 4624

108 3.2 345.6 11664

255 9.3 2371.5 65025

315 12.0 3780.0 99225

405 14.4 5832.0 164025

685 24.5 16782.5 469225

1100 38 41800 1210000

Sum 71091. 3 2024272

According to formula (1.3.8), we have

H 5

1 d

1 1 d

1 d

1 1 d

ð22Þð0:75Þ1 ð68Þð2:4Þ1 1 ð1100Þð38:0Þ

1 68

1 1 1100

71091: 3

2024272

5 0:03512:

1.4 Functions and Their Graphs 41

Thus υ 5 H d 5 0.03512 d. The graph of this equation is given in Figure 8, with

Hubble’s observations superimposed.

Because d 5 137 for Coma Berenices, we calculate that the corresponding

recession velocity is υ 5 0.035 12 137, or υ 5 4.811. Because the units for υ are

thousands of miles per second, our estimate amounts to 4811 mi/s. In fact, Hubble

measured the recession velocity of Coma Berenices to be 4700 mi/s.

INSIGHT

The constant H is known as Hubble’s constant. A dimension analysis

shows that 1/H represents a time because the equation υ 5 H d implies

distance

distance=time

5 time:

Hydra

Bootes

Gemini

Leo

Ursa Major 1

Perseus

Virgo

Pegasus

1200

1000800600400200

Distance

Recession Velocity

m Figure 7

v  Hd

1200

1000800600400200

Distance

Recession Velocity

(137, 4811)

Coma Berenices

m Figure 8

42 Chapter

1 Basics

In the Big Bang theory of the universe, 1/H represents the age of the universe. Reﬁne-

ments in astronomical measurements have led to corrections to Hubble’s data and to

revised estimates of H. Data obtained from the Wilkinson Microwave Anisotropy Probe

(WMAP) released in February 2008 suggest that the universe is approximately 13.73

billion years old.

By “transforming” data, the method of least squares can often be applied in

instances when a scatter plot is not linear. For example, suppose that z 5 A k

where A is a known constant, and k is a ﬁxed base that is to be determined. We

apply log

to each side of the equation z 5 A k

. Using the logarith m laws

log

(u υ) 5 log

(u) 1 log

(υ) and log

) 5 p log

(u), we obtain

log

ðzÞ5 log

ðA  k

5 log

ðAÞ1 log

ðk

5 log

ðAÞ1 x  log

ðkÞ:

If we set y 5 log

(z), m 5 log

(k), and b 5 log

(A), then the transformed equa-

tion becomes the linear equation

y 5 m  x 1 b

in the variables x and y.

⁄ EX

AMPLE 12 A radioactive isotope of gold is used to diagnose arthritis.

Let f (x) denote the fraction of blood serum gold remaining in the pa tient at the

time x days after the initial dose. Measured values of f (x) for x 5 1, 2, . . . , 8 are

listed in the table.

Days x 01

2 3 4 5 6 7 8

Serum gold (z) 1.0 0.91 0.77 0.66 0.56 0.49 0.43 0.38 0.34

Find a positive constant k such

that z 5 k

is a model for f (x). Use the model to

predict the fraction of the initial dose that remains in the blood serum after ten

days.

Solution Figure

9a shows the scatter plot of this data. Following the discussion that

precedes this example, we apply log

to each side of z 5 k

to obtain the linear

equation

y 5 log

ðzÞ5 log

ðk

Þ5 x  log

ðkÞ5 m  x

where m 5 log

(k). Because the line y 5 m x passes through the origin, we pass

the regression line through the data point (0, 0). With x

5 0, y

5 0, and N 5 8,

equation (1.3.8) becomes

m 5

1 x

1 1 x

1 x

1 1 x

642

0.4

0.6

0.5

0.7

0.9

0.8

1.0

Time

(

days

)

Blood Serum Gold

m Figure 9a

1.4 Functions and Their Graphs 43

The values that we need for the calculation of m can be found in the following

table.

xzy5 log

( y) x yx

1 0.91 20.0409 20.0409 1

2 0.77 20.1135 20.2270 4

3 0.66 20.1804 20.5414 9

4 0.56 20.2518 21.0073 16

5 0.49 20.3098 21.5490 25

6 0.43 20.3665 22.1992 36

7 0.38 20.4202 22.9415 49

8 0.34 20.4685 23.7482 64

Sum 212.2545 204

Our estimate of m is 212.2545/204,

or m 520.06.

Figure 9b shows the transformed data points, along with the least squares line

y 520.06x. Our estimate for m provides an estimate for the base k, namely

k 5 10

20.06

0.87. In Figure 9c, the grap h of y 5 0.87

is superimposed on the

original scatter plot. The predicted value of the serum gold concentration ten days

after the initial dose is f (10) 5 0.87

0.25. ¥

y  mx

m  0.06

108

642

0.6

0.5

0.4

0.3

0.2

0.1

Time (days)

Blood Serum Gold (log

)

m Figure 9b

642

0.4

0.3

0.6

0.5

0.7

0.9

0.8

1.0

Time

(

)

Blood Serum Gold

z  0.87

Extrapolated

point

m Figure 9c

44 Chapter

1 Basics