Bird J. Electrical Circuit Theory and Technology
Подождите немного. Документ загружается.


37 A numerical method of
harmonic analysis
At the end of this chapter you should be able to:
ž use a tabular method to determine the Fourier series for a
complex waveform
ž predict the probable harmonic content of a waveform on
inspection
37.1 Introduction
Many practical waveforms can be represented by simple mathematical
expressions, and, by using Fourier series, the magnitude of their harmonic
components determined. For waveforms not in this category, analysis may
be achieved by numerical methods. Harmonic analysis is the process of
resolving a periodic, non-sinusoidal quantity into a series of sinusoidal
components of ascending order of frequency.
37.2 Harmonic analysis
on data given in tabular
or graphical form
A Fourier series is merely a trigonometric series of the form:
fx D a
0
C a
1
cosx C a
2
cos2x CÐÐÐCb
1
sinx C b
2
sin2x CÐÐÐ
i.e. fx D a
0
C
1
nD1
a
n
cosnx C b
n
sinnx
The Fourier coefficients a
0
, a
n
and b
n
all require functions to be inte-
grated, i.e.,
a
0
D
1
2
fxdx D
1
2
2
0
fx dx
D mean value of fx in the range to or0to2
a
n
D
1
fx cosnx dx D
1
2
0
fx cos nx dx
D twice the mean value of fx cosnx in the range 0 to 2
b
n
D
1
fx sin nx dx D
1
2
0
fx sin nx dx
D twice the mean value of fx sinnx in the range 0 to 2
A numerical method of harmonic analysis 679
However, irregular waveforms are not usually defined by mathematical
expressions and thus the Fourier coefficients cannot be determined by
using calculus. In these cases, approximate methods, such as the trape-
zoidal rule, can be used to evaluate the Fourier coefficients.
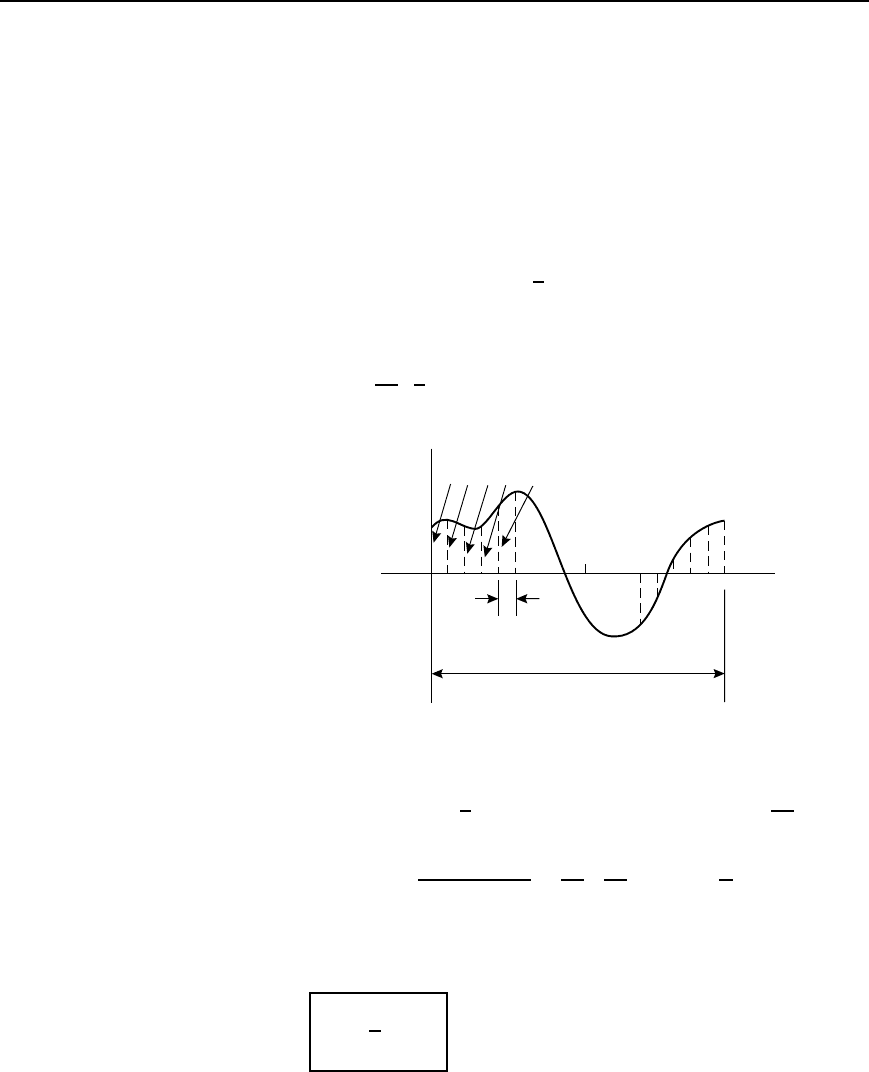
Most practical waveforms to be analysed are periodic. Let the period
of a waveform be 2 and be divided into p equal parts as shown in
Figure 37.1. The width of each interval is thus 2/p. Let the ordinates
be labelled y
0
, y
1
, y
2
, ..., y
p
(note that y
0
D y
p
). The trapezoidal rule
states:
Area ³ (width of interval)
1
2
(first C last ordinate)
C sum of remaining ordinates
³
2
p
1
2
y
0
C y
p
C y
1
C y
2
C y
3
CÐÐÐ
f(x)
y
0
y
1
y
2
y
3
y
4
y
p
x2p
p
0
2p/p
Period = 2p
Figure 37.1
Since y
0
D y
p
, then
1
2
y
0
C y
p
D y
0
D y
p
. Hence area ³
2
p
p
kD1
y
k
Mean value D
area
length of base
³
1
2
2
p
p
kD1
y
k
³
1
p
p
kD1
y
k
However, a
0
D mean value of fx in the range 0 to 2. Thus
a
0
≈
1
p
p
k=1
y
k
37.1
Similarly, a
n
D twice the mean value of fx cosnx in the range
0to2, thus,

680 Electrical Circuit Theory and Technology
a
n
≈
2
p
p
k=1
y
k
cosnx
k
37.2
and b
n
D twice the mean value of fx sinnx in the range 0 to 2, thus
b
n
≈
2
p
p
k=1
y
k
sinnx
k
37.3
Problem 1. The values of the voltage volts at different moments
in a cycle are given by:
degrees 30 60 90 120 150 180 210 240 270 300 330 360
(volts) 62 35 38 64 63 52 28 24 80 96 90 70
Draw the graph of voltage against angle and analyse the voltage
into its first three constituent harmonics, each coefficient correct to
2 decimal places.
The graph of voltage against angle is shown in Figure 37.2. The
range0to2 is divided into 12 equal intervals giving an interval width
of 2/12, i.e. /6or30
°
. The values of the ordinates y
1
, y
2
, y
3
, ... are
62, 35, 38, ... from the given table of values. If a larger number of
intervals are used, results having a greater accuracy are achieved. The
data is tabulated in the proforma shown in Table 37.1.
y
1
y
2
y
3
y
4
y
5
y
6
y
7
y
8
y
9
y
11
y
12
y
10
270 360 degrees
90 180
80
60
40
20
0
−20
−40
−60
−80
Voltage v (volts)
q
Figure 37.2
From equation (37.1), a
0
³
1
p
p
kD1
y
k
D
1
12
212
D 17.67 (since p D 12
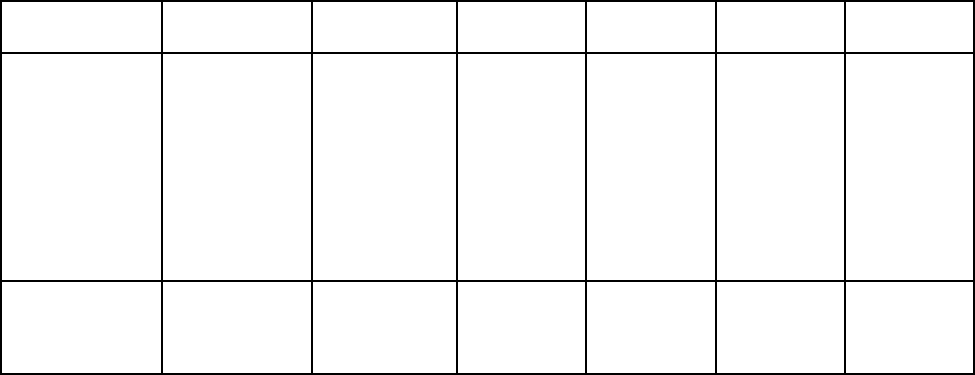
TABLE 37.1
Ordin-
°
v cos v cos sin v sin cos2 v cos2 sin2 v sin 2 cos 3 v cos3 sin3 v sin 3
ates
y
1
30 62 0.866 53.69 0.5 31 0.5 31 0.866 53.69 00 162
y
2
60 35 0.5 17.5 0.866 30.31 0.5 17.5 0.866 30.31 1 35 00
y
3
90 38 00 1 38 138 00 00138
y
4
120 64 0.5 32 0.866 55.42 0.5 32 0.866 55.42 1 64 00
y
5
150 63 0.866 54.56 0.5 31.5 0.5 31.5 0.866 54.56 00 1 63
y
6
180 52 152 001 52 00152 00
y
7
210 28 0.866 24.25 0.5 14 0.5 14 0.866 24.25 00128
y
8
240 24 0.5 12 0.866 20.78 0.5 12 0.866 20.78 124 00
y
9
270 80 001 80 1 80 00 00 180
y
10
300 96 0.5 48 0.866 83.14 0.5 48 0.866 83.14 1 96 00
y
11
330 90 0.866 77.94 0.5 45 0.5 45 0.866 77.94 001 90
y
12
360 70 170 00170 00 170 00
12
kD1
y
k
D 212
12
kD1
y
k
cos
k
12
kD1
y
k
sin
k
12
kD1
y
k
cos2
k
12
kD1
y
k
sin2
k
12
kD1
y
k
cos3
k
12
kD1
y
k
sin3
k
D417.94 D278.53 D39 D29.43 D49 D55

682 Electrical Circuit Theory and Technology
From equation (37.2), a
n
³
2
p
p
kD1
cosnx
k
Hence a
1
³
2
12
417.94 D 69.66I
a
2
³
2
12
39 D6.50I
and a
3
³
2
12
49 D8.17
From equation (37.3), b
n
³
2
p
p
kD1
y
k
sinnx
k
Hence b
1
³
2
12
278.53 D46.42;
b
2
³
2
12
29.43 D 4.91;
and b
3
³
2
12
55 D 9.17
Substituting these values into the Fourier series:
fx D a
0
C
1
nD1
a
n
cosnx C b
n
sinnx
gives: n
= 17.67 Y 69.66cosq − 6.50cos2q − 8.17cos3q Y ···
−
46.42sinq Y 4.91sin2q Y 9.17sin3q Y ··· 37.4
Note that in equation (37.4), (46.42sin C69.66cos ) comprises the
fundamental, (4.91sin2 6.50cos2) comprises the second harmonic
and (9.17 sin3 8.17cos3) comprises the third harmonic.
It is shown in Higher Engineering Mathematics that
a sinωt C b cosωt R sinωt C ˛
where a D R cos ˛, b D R sin ˛, R D
a
2
C b
2
and ˛ D arctan
b
a
For the fundamental, R D
46.42
2
C 69.66
2
D 83.71
If a D R cos˛, then cos ˛ D
a
R
D
46.42
83.71
which is negative,
and if b D R sin˛, then sin ˛ D
b
R
D
69.66
83.71
which is positive.
The only quadrant where cos˛ is negative and sin ˛ is positive is the
second quadrant.
Hence ˛ D arctan
b
a
D arctan
69.66
46.42
D 123.68
°
or 2. 16 rad
Thus (46.42 sin C 69.66 cos D 83.71sin C 2.16)
A numerical method of harmonic analysis 683
By a similar method it may be shown that the second harmonic
4.91 sin 2 6.50cos2 8.15sin2 0.92 and the third harmonic
9.17 sin 3 8.17cos3 12.28sin3 0.73
Hence equation (37.4) may be re-written as:
n
= 17.67 Y 83.71sin.q Y 2.16/ Y 8.15sin.2q − 0.92/
Y 12.28sin.3q
− 0.73/ volts
which is the form used in Chapter 36 with complex waveforms.
37.3 Complex waveform
considerations
It is sometimes possible to predict the harmonic content of a waveform
on inspection of particular waveform characteristics.
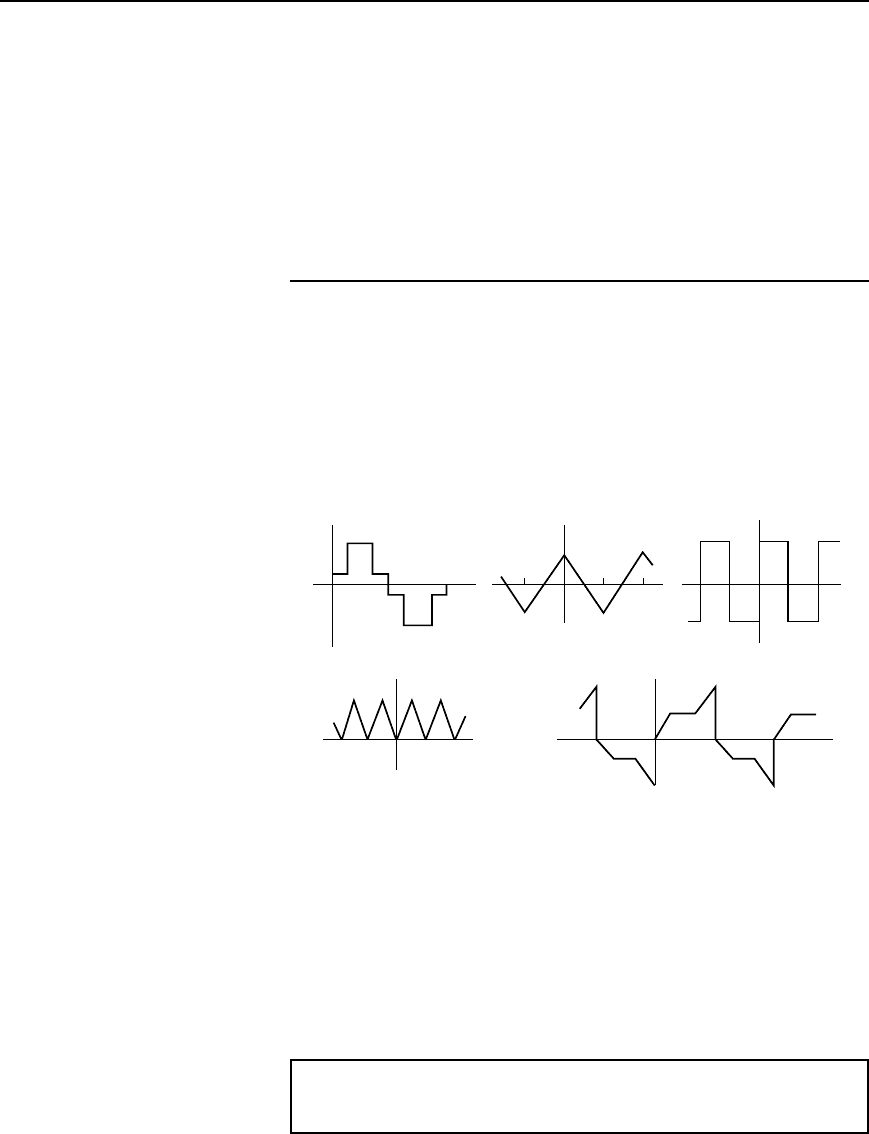
(i) If a periodic waveform is such that the area above the horizontal
axis is equal to the area below then the mean value is zero. Hence
a
0
D 0 (see Figure 37.3(a)).
(ii) An even function is symmetrical about the vertical axis and
contains no sine terms (see Figure 37.3(b)).
f(x)
0 p 2p x
(a)
p 2p x0−p
Contains no sine terms
(b)
−2p −pp02p x
Contains no cosine terms
(c)
f(x)
−2p −pp02p x
f(x)
−pp02p x
Contains only odd harmonics(d) Contains only even harmonics
f(x) f(x)
a
0
= 0
(e)
Figure 37.3
(iii) An odd function is symmetrical about the origin and contains no
cosine terms (see Figure 37.3(c)).
(iv) fx D fx C represents a waveform which repeats after half a
cycle and only even harmonics are present (see Figure 37.3(d)).
(v) fx Dfx C represents a waveform for which the positive
and negative cycles are identical in shape and only odd harmonics
are present (see Figure 37.3(e)).
Problem 2. Without calculating Fourier coefficients state which
harmonics will be present in the waveforms shown in Figure 37.4.
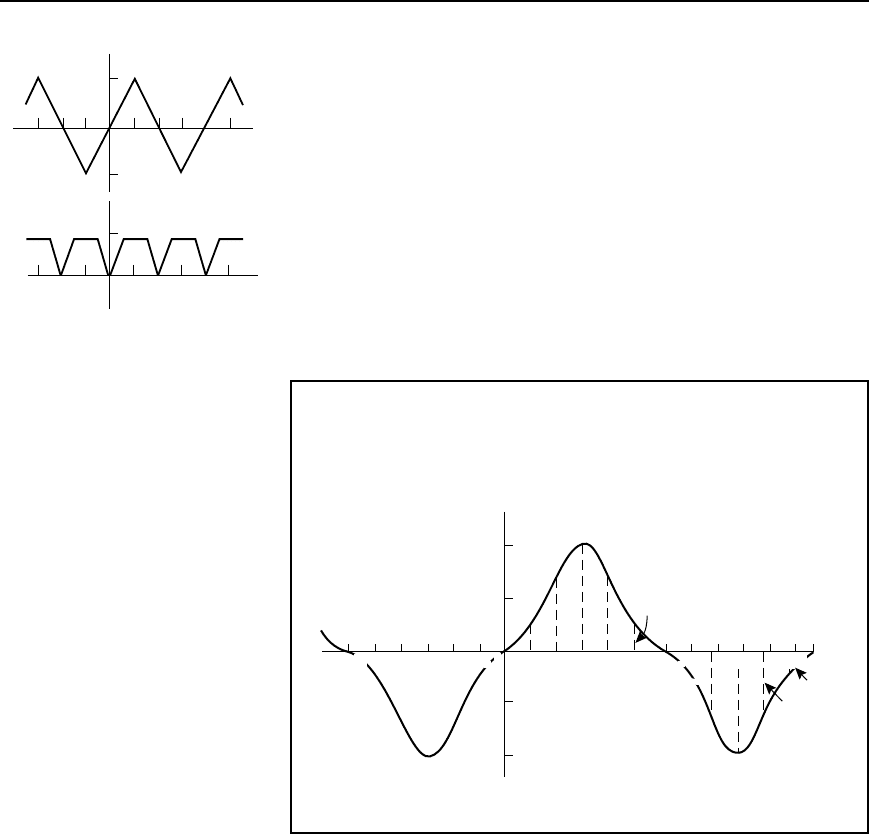
684 Electrical Circuit Theory and Technology
f(x)
2
−2
0 p−p 2p x
0 p−p 2p x
5
f(x)
(a)
(b)
Figure 37.4
(a) The waveform shown in Figure 37.4(a) is symmetrical about the
origin and is thus anodd function. An odd function contains no cosine
terms. Also, the waveform has the characteristic fx Dfx C ,
i.e. the positive and negative half cycles are identical in shape. Only
odd harmonics can be present in such a waveform. Thus the wave-
form shown in Figure 37.4(a) contains only odd sine terms. Since
the area above the x-axis is equal to the area below, a
0
D 0.
(b) The waveform shown in Figure 37.4(b) is symmetrical about the
fx axis and is thus an even function. An even function contains no
sine terms. Also, the waveform has the characteristic fx D fx C
, i.e., the waveform repeats itself after half a cycle. Only even
harmonics can be present in such a waveform. Thus the waveform
shown in Figure 37.4(b) contains only even cosine terms (together
with a constant term, a
0
).
Problem 3. An alternating current i amperes is shown in
Figure 37.5. Analyse the waveform into its constituent harmonics
as far as and including the fifth harmonic, correct to 2 decimal
places, by taking 30
°
intervals.
y
1
y
2
y
3
180 240 300
q
°
1501209060
5
0
−90−150
−180 −120 −60
10
−5
−10
210 270 330
y
8
y
9
y
10
y
11
360
Current i amperes
y
7
30
y
4
y
5
−30
Figure 37.5
With reference to Figure 37.5, the following characteristics are noted:
(i) The mean value is zero since the area above the axis is equal
to the area below it. Thus the constant term, or d.c. component,
a
0
D 0.
(ii) Since the waveform is symmetrical about the origin the function i
is odd, which means that there are no cosine terms present in the
Fourier series.
(iii) The waveform is of the form f Df C which means that
only odd harmonics are present.
Investigating waveform characteristics has thus saved unnecessary
calculations and in this case the Fourier series has only odd sine terms
A numerical method of harmonic analysis 685
present, i.e.
i D b
1
sin Cb
3
sin3 C b
5
sin5 CÐÐÐ
A proforma, similar to Table 37.1, but without the ‘cosine terms’ columns
and without the ‘even sine terms’ columns in shown in Table 37.2 up to,
and including, the fifth harmonic, from which the Fourier coefficients b
1
,
b
3
and b
5
can be determined. Twelve coordinates are chosen and labelled
y
1
, y
2
, y
3
, ...y
12
as shown in Figure 37.5.
TABLE 37.2
Ordinate
°
i sin isin sin 3isin3 sin5isin 5
y
1
30 2 0.5 1 120.5 1
y
2
60 7 0.866 6.06 000.866 6.06
y
3
90 10 110 1 10 110
y
4
120 7 0.866 6.06 000.866 6.06
y
5
150 2 0.5 1 120.5 1
y
6
180 0 00 0000
y
7
210 2 0.5 1 120.5 1
y
8
240 7 0.866 6.06 000.866 6.06
y
9
270 10 110 1 10 110
y
10
300 7 0.866 6.06 000.866 6.06
y
11
330 2 0.5 1 120.5 1
y
12
360 0 00 0000
12
kD1
i
k
sin
k
12
kD1
i
k
sin3
k
12
kD1
i
k
sin5
k
D48.24 D12 D0.24
From equation (37.3), Section 37.2, b
n
³
2
p
p
kD1
i
k
sinn
k
, where p D 12.
Hence b
1
³
2
12
48.24 D 8.04;
b
3
³
2
12
12 D2.00;
and b
5
³
2
12
0.24 D0.04
Thus the Fourier series for current i is given by:
i
= 8.04sinq − 2.00 sin3q − 0.04sin5q
37.4 Further problems
on a numerical method of
harmonic analysis
Determine the Fourier series to represent the periodic functions given by
the tables of values in Problems 1 to 3, up to and including the third
harmonics and each coefficient correct to 2 decimal places. Use 12 ordi-
nates in each case.
686 Electrical Circuit Theory and Technology
1
Angle
°
30 60 90 120 150 180 210 240 270 300 330 360
Displacement y 40 43 38 30 23 17 11 9 10 13 21 32
[y D 23.92 C7.81cos C 14.61sin C 0.17cos2
C 2.31sin2 0.33cos3 C 0.50sin3]
2
Angle
°
0 30 60 90 120 150 180 210 240 270 300 330
Voltage 5.0 1.5 6.0 12.5 16.0 16.5 15.0 12.5 6.5 4.0 7.0 7.5
[ D 5.00 10.78cos C 6.83 sin 1.96cos2
C 0.80 sin2 C 0.58cos3 1.08sin3]
3
Angle
°
30 60 90 120 150 180 210 240 270 300 330 360
Current i 0 1.4 1.8 1.9 1.8 1.3 0 2.2 3.8 3.9 3.5 2.5
[i D 0.64 C 1.58cos 2.73sin 0.23cos2
0.42sin2 C 0.27cos3 C 0.05sin3]
f(t)
4
0
−4
−p−2pp2p 4p t
(a)
2p
−p 0
p
y
10
−10
(b)
x
Figure 37.6
4 Without performing calculations, state which harmonics will be
present in the waveforms shown in Figure 37.6.
[(a) only odd cosine terms present
(b) only even sine terms present]
Figure 37.7

A numerical method of harmonic analysis 687
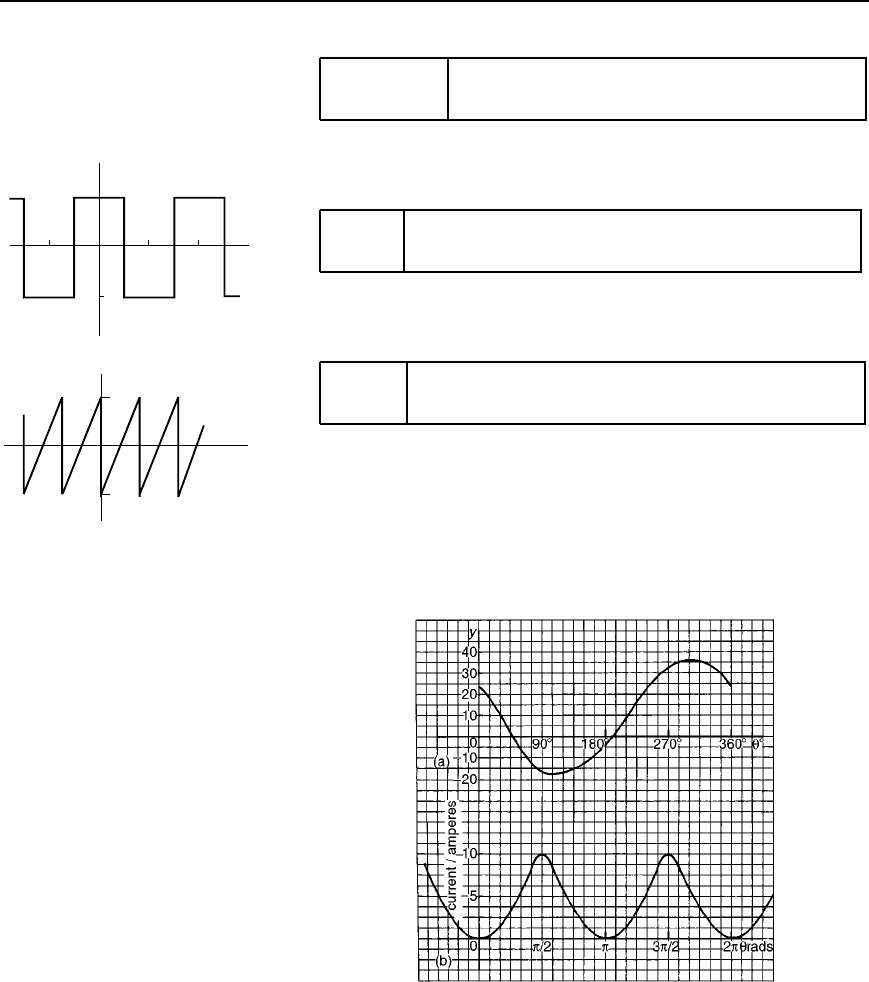
5 Analyse the periodic waveform of displacement y against angle in
Figure 37.7(a) into its constituent harmonics as far as and including
the third harmonic, by taking 30
°
intervals.
[yD 9.4 C 13.2cos 24.4sin C1.75cos 2
0.58 sin2 C 1.33cos3 C 0.67sin3]
6 For the waveform of current shown in Figure 37.7(b) state why only
a d.c. component and even cosine terms will appear in the Fourier
series and determine the series, using /6 rad intervals, up to and
including the sixth harmonic.
[I D 3.83 4.50 cos2 C 1.17cos4 1.00cos6]
