Bird J. Electrical Circuit Theory and Technology
Подождите немного. Документ загружается.

648 Electrical Circuit Theory and Technology
mean value and the maximum value are equal. Thus, if a complex wave-
form should contain a d.c. component I
0
, then the rms current I is given by
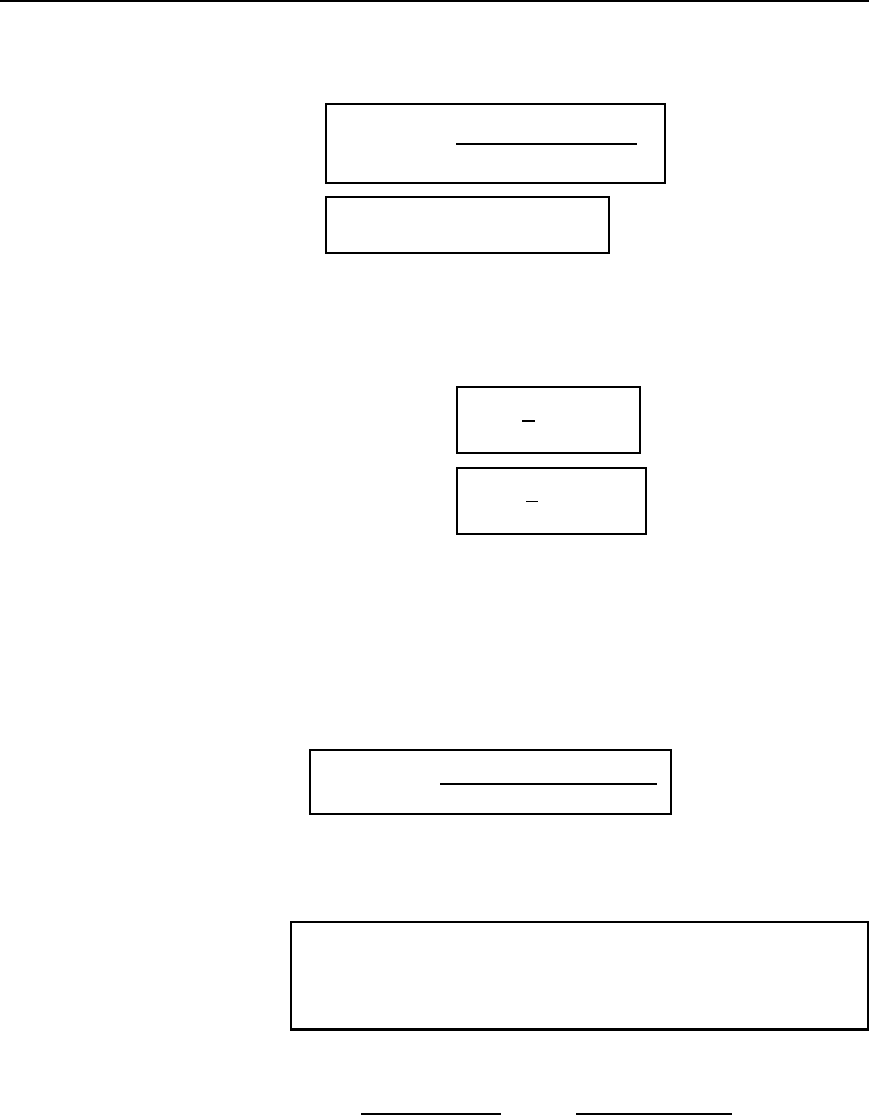
I =
I
2
0
Y
I
2
1m
Y I
2
2m
Y ···Y I
2
nm
2
36.9
or
I =
.I
2
0
Y I
2
1
Y I
2
2
Y ···Y I
2
n
/
36.9
Mean value
The mean or average value of a complex quantity whose negative half-
cycle is similar to its positive half-cycle is given, for current, by
I
av
=
1
p
p
0
id.!t/
36.10
and for voltage by
v
av
=
1
p
p
0
v d.!t/
36.11
each waveform being taken over half a cycle.
Unlike rms values, mean values are affected by the relative phase
angles of the harmonic components.
Form factor
The form factor of a complex waveform whose negative half-cycle is
similar in shape to its positive half-cycle is defined as:
form factor D
rms value of the waveform
mean value
36.12
where the mean value is taken over half a cycle.
Changes in the phase displacement of the harmonics may appreciably
alter the form factor of a complex waveform.
Problem 3. Determine the rms value of the current waveform
represented by
i D 100sinωt C 20sin3ωt C /6 C 10 sin5ωt C 2/3mA
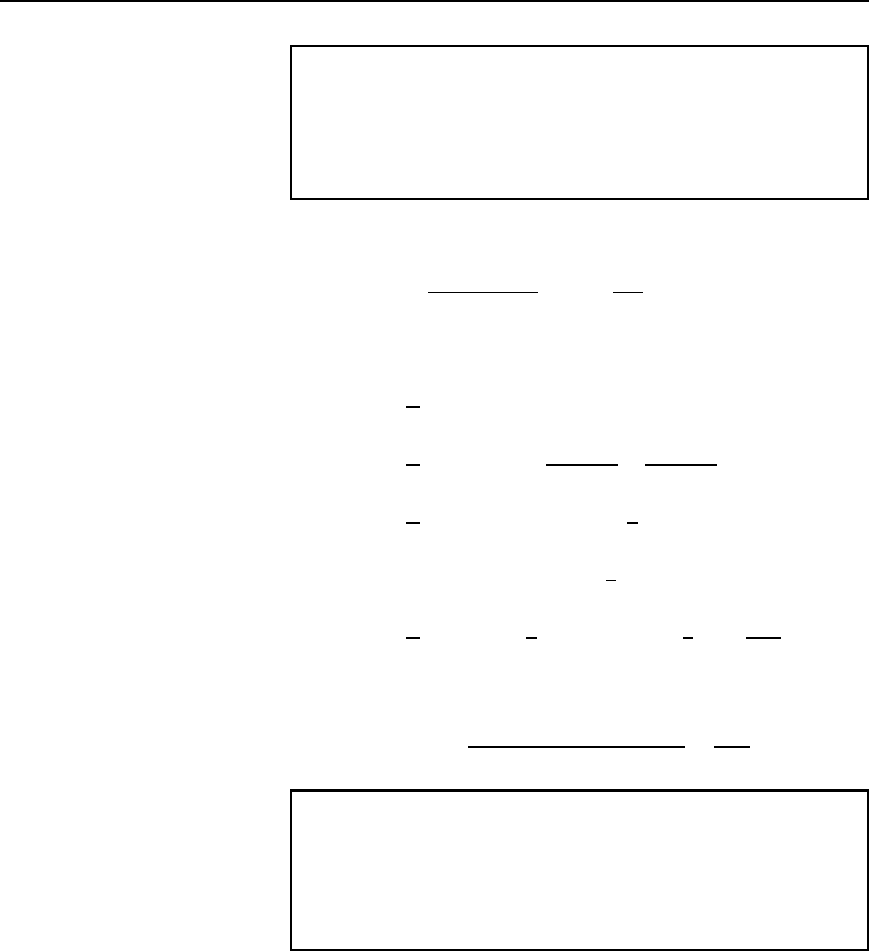
From equation (36.5), the rms value of current is given by
I D
100
2
C 20
2
C 10
2
2
D
10000 C 400 C 100
2
D 72.46 mA
Complex Waveforms 649
Problem 4. A complex voltage is represented by
v D 10sinωt C 3 sin 3ωt C 2 sin 5ωtvolts
Determine for the voltage, (a) the rms value, (b) the mean value
and (c) the form factor.
(a) From equation (36.7), the rms value of voltage is given by
V D
10
2
C 3
2
C 2
2
2
D
113
2
D 7.52 V
(b) From equation (36.11), the mean value of voltage is given by
V
av
D
1
0
10 sin ωt C 3sin 3ωt C 2sin 5ωt dωt
D
1
10cosωt
3cos3ωt
3
2cos5ωt
5
0
D
1
10cos cos 3
2
5
cos5
10cos0 cos 0
2
5
cos0
D
1
10 C 1 C
2
5
10 1
2
5
D
22.8
D 7.26 V
(c) From equation (36.12), form factor is given by
form factor D
rms value of the waveform
mean value
D
7.52
7.26
D 1.036
Problem 5. A complex voltage waveform which has an rms value
of 240 V contains 30% third harmonic and 10% fifth harmonic,
both of the harmonics being initially in phase with each other. (a)
Determine the rms value of the fundamental and each harmonic.
(b) Write down an expression to represent the complex voltage
waveform if the frequency of the fundamental is 31.83 Hz.
(a) From equation (36.8), rms voltage V D
V
2
1
C V
2
3
C V
2
5
.
Since V
3
D 0.30 V
1
,V
5
D 0.10 V
1
and V D 240 V, then
240 D
[V
2
1
C 0.30 V
1
2
C 0.10 V
1
2
]
i.e., 240 D
1.10 V
2
1
D 1.049 V
1
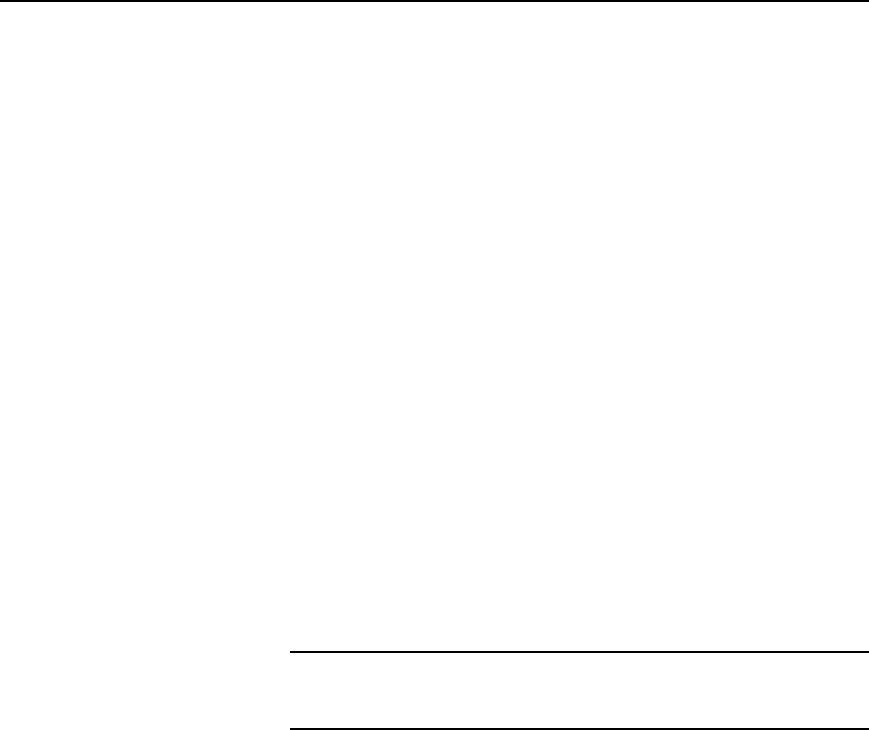
650 Electrical Circuit Theory and Technology
from which the rms value of the fundamental,
V
1
D 240/1.049 D 228.8V.
Rms value of the third harmonic,
V
3
D 0.30 V
1
D 0.30228.8 D 68.64 V
and the rms value of the fifth harmonic,
V
5
D 0.10 V
1
D 0.10228.8 D 22.88 V
(b) Maximum value of the fundamental,
V
1m
D
p
2V
1
D
p
2228.8 D 323.6V
Maximum value of the third harmonic,
V
3m
D
p
2V
3
D
p
268.64 D 97.07 V
Maximum value of the fifth harmonic,
V
5m
D
p
2V
5
D
p
222.88 D 32.36 V
Since the fundamental frequency is 31.83 Hz, the funda-
mental voltage may be written as 323.6 sin 231.83t, i.e.,
323.6sin200t volts
The third harmonic component is 97.07 sin600t volts and the fifth
harmonic component is 32.36 sin 1000t volts. Hence an expression
representing the complex voltage waveform is given by
v = .323.6sin200t Y 97.07sin600t Y 32.36sin1000t/volts
Further problems on rms values, mean values and form factor of complex
waves may be found in Section 36.9, problems 7 to 11, page 672.
36.5 Power associated
with complex waves
Let a complex voltage wave be represented by
v D V
1m
sinωt C V
2m
sin2ωt C V
3m
sin3ωt CÐÐÐ,
and when this is applied to a circuit let the resulting current be repre-
sented by
i D I
1m
sinωt
1
C I
2m
sin2ωt
2
C I
3m
sin3ωt
3
CÐÐÐ
(Since the phase angles are lagging, the circuit in this case is inductive.)
At any instant in time the power p supplied to the circuit is given by
p D
vi, i.e.,
p D V
1m
sinωt C V
2m
sin2ωt CÐÐÐI
1m
sinωt
1
C I
2m
sin2ωt
2
CÐÐÐ
D V
1m
I
1m
sinωt sinωt
1
C V
1m
I
2m
sinωt sin2ωt
2
DÐÐÐ
36.13
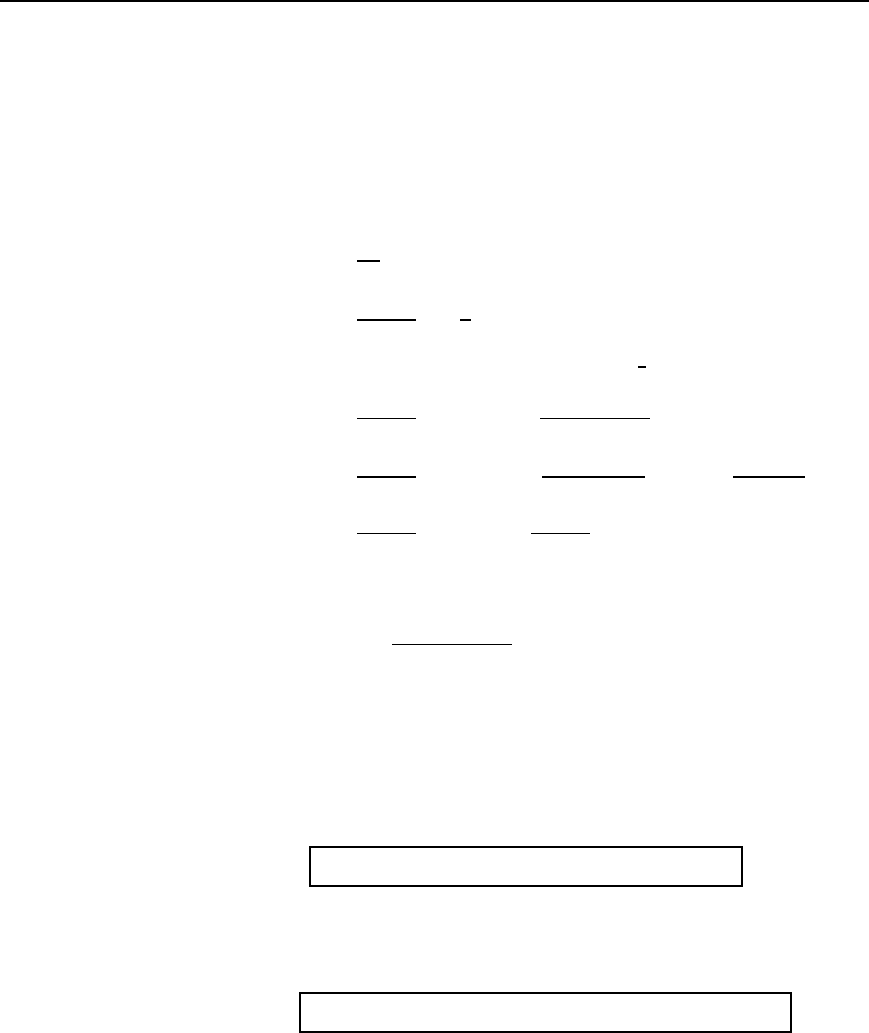
Complex Waveforms 651
The average or active power supplied over one cycle is given by the sum
of the average values of each individual product term taken over one
cycle. It is seen from equation (36.4) that the average value of product
terms involving harmonics of different frequencies is always zero. This
means therefore that only products of voltage and current harmonics of
the same frequency need be considered in equation (36.13).
Taking the first term, for example, the average power P
1
over one cycle
of the fundamental is given by
P
1
D
1
2
2
0
V
1m
I
1m
sinωt sinωt
1
dωt
D
V
1m
I
1m
2
2
0
1
2
fcos
1
cos2ωt
1
gdωt
since sin A sin B D
1
2
fcosA B cosA C Bg,
D
V
1m
I
1m
4
ωt cos
1
sin2ωt
1
2
2
0
D
V
1m
I
1m
4
2 cos
1
sin4
1
2
0
sin
1
2
D
V
1m
I
1m
4
[2 cos
1
] D
V
1m
I
1m
2
cos
1
V
1m
D
p
2V
1
and I
1m
D
p
2I
1
, where V
1
and I
1
are rms values, hence
P
1
D
p
2V
1
p
2I
1
2
cos
1
i.e., P
1
D V
1
I
1
cos
1
watts
Similarly, the average power supplied over one cycle of the fundamental
for the second harmonic is V
2
I
2
cos
2
, and so on. Hence the total power
supplied by complex voltages and currents is the sum of the powers
supplied by each harmonic component acting on its own. The average
power P supplied for one cycle of the fundamental is given by
P = V
1
I
1
cosf
1
Y V
2
I
2
cosf
2
Y ···Y V
n
I
n
cosf
n
36.14
If the voltage waveform contains a d.c. component V
0
which causes a
direct current component I
0
, then the average power supplied by the d.c.
component is V
0
I
0
and the total average power P supplied is given by
P = V
0
I
0
Y V
1
I
1
cosf
1
Y V
2
I
2
cosf
2
Y ···Y V
n
I
n
cosf
n
36.15
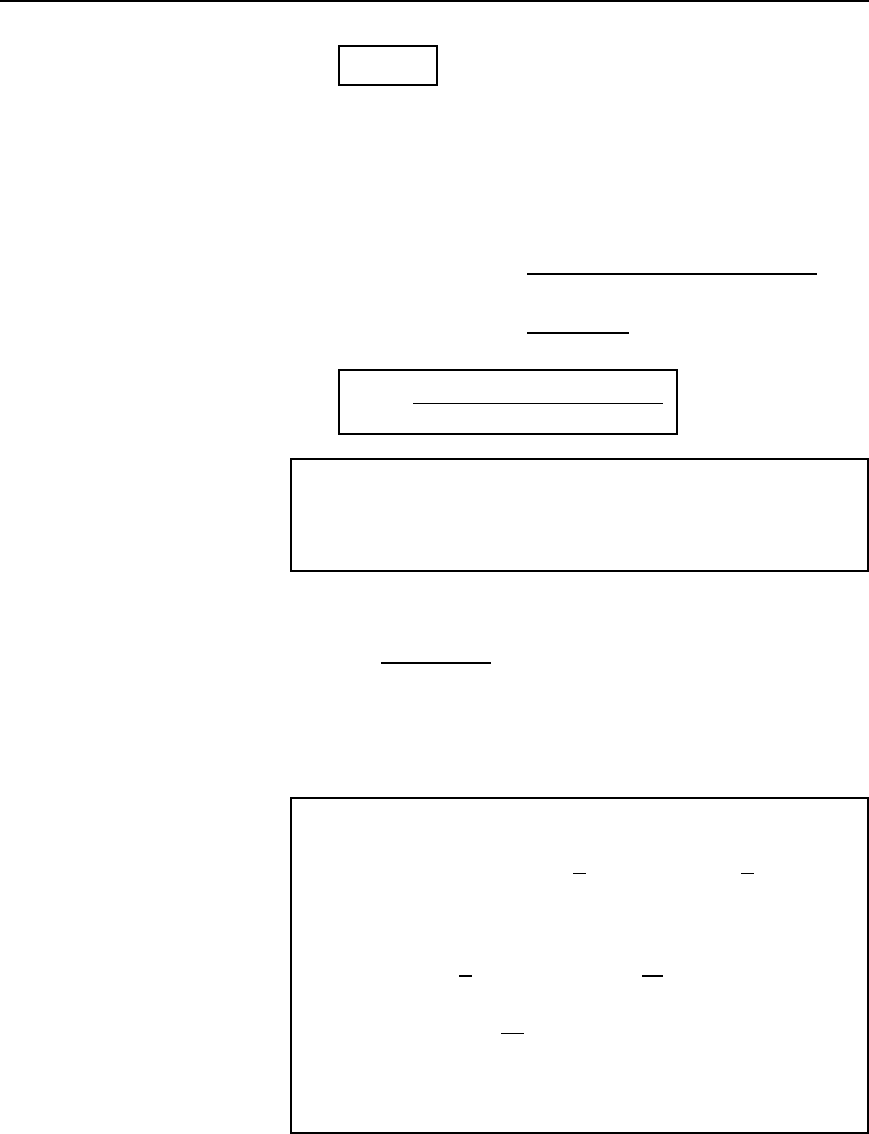
Alternatively, if R is the equivalent series resistance of a circuit then the
total power is given by
P D I
2
0
R C I
2
1
R C I
2
2
R C I
2
3
R CÐÐÐ
652 Electrical Circuit Theory and Technology
i.e.,
P = I
2
R
36.16
where I is the rms value of current i.
Power factor
When harmonics are present in a waveform the overall circuit power
factor is defined as
overall power factor D
total power supplied
total rms voltage ð total rms current
D
total power
volt amperes
i.e.,
p.f . =
V
1
I
1
cosf
1
Y V
2
I
2
cosf
2
Y ···
VI
36.17
Problem 6. Determine the average power in a 20 # resistance if
the current i flowing through it is of the form
i D 12sinωt C 5 sin 3ωt C 2 sin 5ωtamperes
From equation (36.5), rms current,
I D
12
2
C 5
2
C 2
2
2
D 9.30 A
From equation (36.16), average power,
P D I
2
R D 9.30
2
20 D 1730 W or 1.73 kW
Problem 7. A complex voltage v given by
v D 60sinωt C 15 sin
3ωt C
4
C 10sin
5ωt
2
volts
is applied to a circuit and the resulting current i is given by
i D 2sin
ωt
6
C 0.30sin
3ωt
12
C 0.1 sin
5ωt
8
9
amperes
Determine (a) the total active power supplied to the circuit, and (b)
the overall power factor.

Complex Waveforms 653
(a) From equation (36.14), total power supplied,
P D V
1
I
1
cos
1
C V
3
I
3
cos
3
C V
5
I
5
cos
5
D
60
p
2
2
p
2
cos
0
6
C
15
p
2
0.3
p
2
cos
4
12
C
10
p
2
0.1
p
2
cos
2
8
9
D 51.96 C 1.125 C 0.171 D 53.26 W
(b) From equation (36.5), rms current,
I D
2
2
C 0.3
2
C 0.1
2
2
D 1.43 A
and from equation (36.7), rms voltage,
V D
60
2
C 15
2
C 10
2
2
D 44.30 V
From equation (36.17),
overall power factor D
53.26
44.301.43
D 0.841
(With a sinusoidal waveform,
power factor D
power
volt-amperes
D
VI cos
VI
D cos
Thus power factor depends upon the value of phase angle , and is lagging
for an inductive circuit and leading for a capacitive circuit. However,
with a complex waveform, power factor is not given by cos .Inthe
expression for power in equation (36.14), there are n phase-angle terms,
1
,
2
,...,
n
, all of which may be different. It is for this reason that
it is not possible to state whether the overall power factor is lagging or
leading when harmonics are present.)
Further problems on power associated with complex waves may be found
in Section 36.9, problems 12 to 15, page 673.
36.6 Harmonics in
single-phase circuits
When a complex alternating voltage wave, i.e., one containing harmonics,
is applied to a single-phase circuit containing resistance, inductance and/or
capacitance (i.e., linear circuit elements), then the resulting current will
also be complex and contain harmonics.

654 Electrical Circuit Theory and Technology
Let a complex voltage v be represented by
v = V
1m
sin!t Y V
2m
sin2!t Y V
3m
sin3!t Y ···
(a) Pure resistance
The impedance of a pure resistance R is independent of frequency and
the current and voltage are in phase for each harmonic. Thus the general
expression for current i is given by
i =
v
R
=
V
1m
R
sin!t Y
V
2m
R
sin2!t Y
V
3m
R
sin3!t Y
···
36.18
The percentage harmonic content in the current wave is the same as that in
the voltage wave. For example, the percentage second harmonic content
from equation (36.18) is
V
2m
/R
V
1m
/R
ð 100%, i.e.,
V
2m
V
1m
ð 100%
the same as for the voltage wave. The current and voltage waveforms
will therefore be identical in shape.
(b) Pure inductance
The impedance of a pure inductance L, i.e., inductive reactance X
L
D
2fL, varies with the harmonic frequency when voltage v is applied to
it. Also, for every harmonic term, the current will lag the voltage by 90
°
or /2 rad. The current i is given by
i =
v
X
L
=
V
1m
!L
sin
!t −
p
2
Y
V
2m
2!L
sin
2!t −
p
2
Y
V
3m
3!L
sin
3!t −
p
2
Y ···
36.19
since for the nth harmonic the reactance is nωL.
Equation (36.19) shows that for, say, the nth harmonic, the percentage
harmonic content in the current waveform is only 1/n of the corre-
sponding harmonic content in the voltage waveform.
If a complex current contains a d.c. component then the direct voltage
drop across a pure inductance is zero.
(c) Pure capacitance
The impedance of a pure capacitance C, i.e., capacitive reactance X
C
D
1/2fC, varies with the harmonic frequency when voltage
v is applied
to it. Also, for each harmonic term the current will lead the voltage by
90
°
or /2 rad. The current i is given by
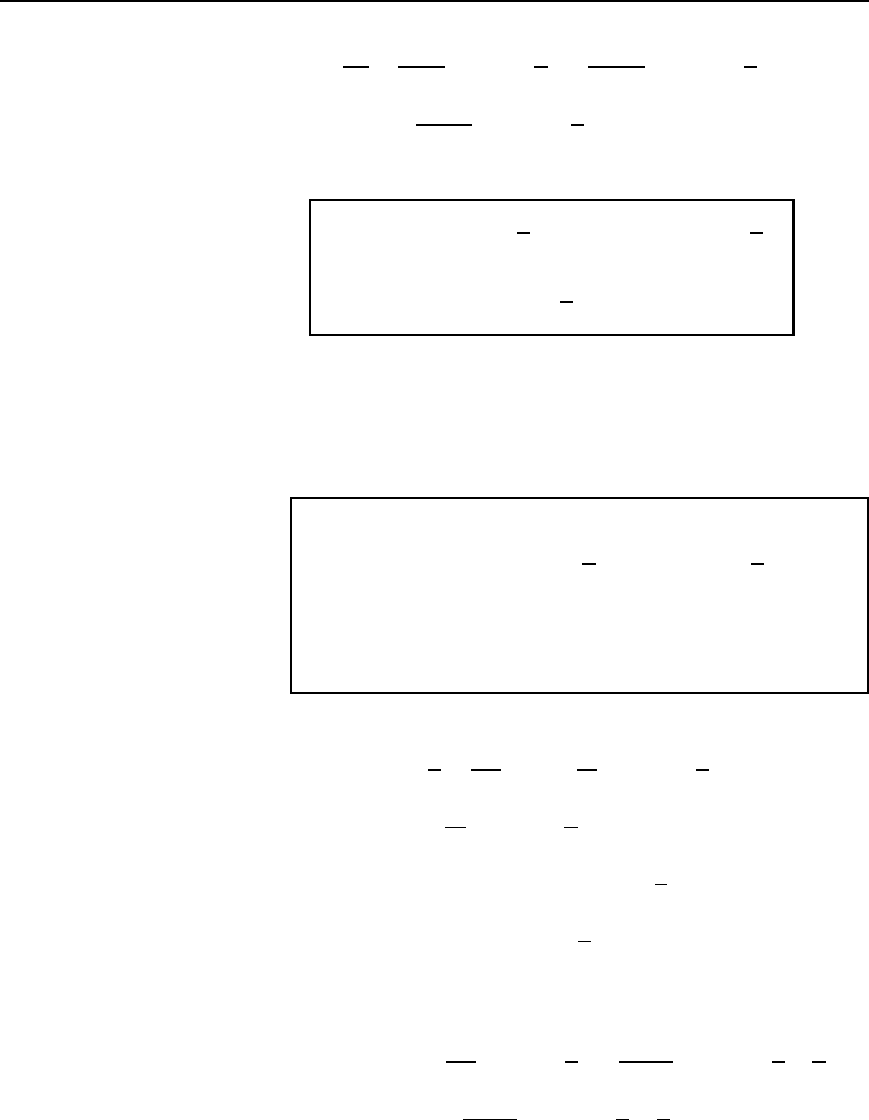
Complex Waveforms 655
i D
v
X
C
D
V
1m
1/ωC
sin
ωt C
2
C
V
2m
1/2ωC
sin
2ωt C
2
C
V
3m
1/3ωC
sin
3ωt C
2
CÐÐÐ,
since for the nth harmonic the reactance is 1/nωC. Hence current,
i= V
1m
.!C/ sin
!t Y
p
2
Y V
2m
.2!C/ sin
2!t Y
p
2
Y V
3m
.3!C/ sin
3!t Y
p
2
Y ···
36.20
Equation (36.20) shows that the percentage harmonic content of the
current waveform is n times larger for the nth harmonic than that of
the corresponding harmonic voltage.
If a complex current contains a d.c. component then none of this direct
current will flow through a pure capacitor, although the alternating compo-
nents of the supply still operate.
Problem 8. A complex voltage waveform represented by
v D 100sinωt C 30 sin
3ωt C
3
C 10sin
5ωt
6
volts
is applied across (a) a pure 40 # resistance, (b) a pure 7.96 mH
inductance, and (c) a pure 25
µF capacitor. Determine for each case
an expression for the current flowing if the fundamental frequency
is 1 kHz.
(a) From equation (36.18),
current i D
v
R
D
100
40
sinωt C
30
40
sin
3ωt C
3
C
10
40
sin
5ωt
6
i.e. i= 2.5sin!t Y 0.75sin
3!t Y
p
3
Y 0.25sin
5!t −
p
6
amperes
(b) At the fundamental frequency, ωL D 210007.96 ð 10
3
D
50 #. From equation (36.19),
current i D
100
50
sin
ωt
2
C
30
3 ð 50
sin
3ωt C
3
2
C
10
5 ð 50
sin
5ωt
6
2
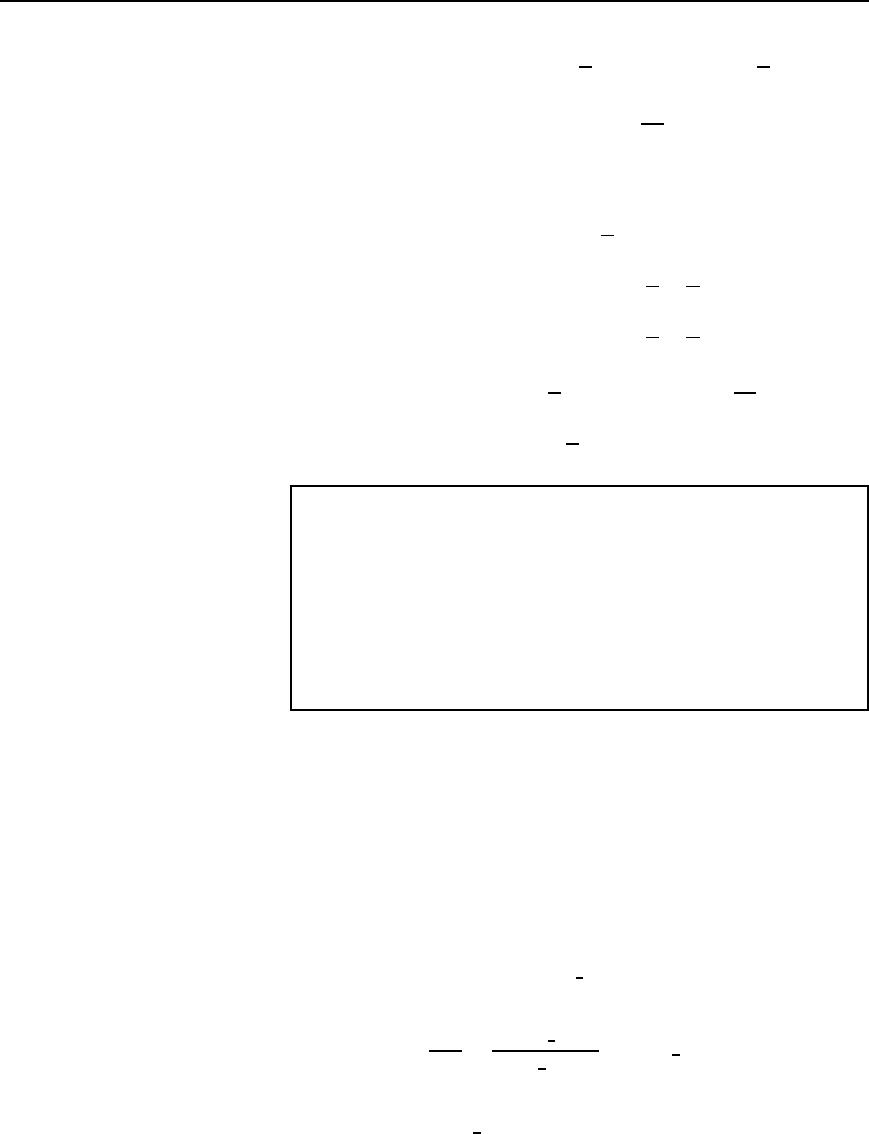
656 Electrical Circuit Theory and Technology
i.e. current i = 2sin
!t −
p
2
Y0.20sin
3!t −
p
6
Y 0.04sin
5!t −
2p
3
amperes
(c) At the fundamental frequency, ωC D 2100025 ð 10
6
D
0.157. From equation (36.20),
current i D 1000.157 sin
ωt C
2
C 303 ð0.157 sin
3ωt C
3
C
2
C 105 ð0.157 sin
5ωt
6
C
2
i.e., i = 15.70sin
!t Y
p
2
Y14.13sin
3!t Y
5p
6
Y7.85sin
5!t Y
p
3
amperes
Problem 9. A supply voltage v given by
v D 240sin314t C 40 sin 942t C 30 sin 1570tvolts
is applied to a circuit comprising a resistance of 12 # connected in
series with a coil of inductance 9.55 mH. Determine (a) an expres-
sion to represent the instantaneous value of the current, (b) the rms
voltage, (c) the rms current, (d) the power dissipated, and (e) the
overall power factor.
(a) The supply voltage comprises a fundamental, 240sin314t, a third
harmonic, 40sin942t (third harmonic since 942 is 3 ð 314) and a
fifth harmonic, 30sin1570t.
Fundamental
Since the fundamental frequency, ω
1
D 314 rad/s, inductive reac-
tance,
X
L1
D ω
1
L D 3149.55 ð 10
3
D 3.0 #.
Hence impedance at the fundamental frequency,
Z
1
D 12 C j3.0# D 12.37
6
14.04
°
#
Maximum current at fundamental frequency
I
1m
D
V
1m
Z
1
D
240
6
0
°
12.37
6
14.04
°
D 19.40
6
14.04
°
A
14.04
°
D 14.04 ð /180 rad D 0.245 rad, thus
I
1m
D 19.40
6
0.245 A

Complex Waveforms 657
Hence the fundamental current i
1
D 19.40sin314t 0.245A.
(Note that with an expression of the form R sinωt š ˛, ωt is an
angle measured in radians, thus the phase displacement, ˛, should
also be expressed in radians.)
Third harmonic
Since the third harmonic frequency, ω
3
D 942 rad/s, inductive
reactance,
X
L3
D 3X
L1
D 9.0 #.
Hence impedance at the third harmonic frequency,
Z
3
D 12 C j9.0# D 15
6
36.87
°
#
Maximum current at the third harmonic frequency,
I
3m
D
V
3m
Z
3
D
40
6
0
°
15
6
36.87
°
D 2.67
6
36.87
°
A
D 2.67
6
0.644 A
Hence the third harmonic current, i
3
D 2.67sin942t 0.644A.
Fifth harmonic
Inductive reactance, X
L5
D 5X
L1
D 15 #
Impedance Z
5
D 12 C j15# D 19.21
6
51.34
°
#
Current, I
5m
D
V
5m
Z
5
D
30
6
0
°
19.21
6
51.34
°
D 1.56
6
51.34
°
A D 1.56
6
0.896 A
Hence the fifth harmonic current, i
5
D 1.56sin1570t 0.896A
Thus an expression to represent the instantaneous current, i, is given
by i D i
1
C i
3
C i
5
i.e.,
i
= 19.40sin.314t − 0.245/ Y 2.67sin.942t − 0.644/ Y
1.56sin.1570t
− 0.896/amperes
(b) From equation (36.7), rms voltage,
V D
240
2
C 40
2
C 30
2
2
D 173.35 V
(c) From equation (36.5), rms current,
I D
19.40
2
C 2.67
2
C 1.56
2
2
D 13.89 A
