Bird J. Electrical Circuit Theory and Technology
Подождите немного. Документ загружается.


628 Electrical Circuit Theory and Technology
14 A single-phase, 240 V/2880 V ideal transformer is supplied from a
240 V source through a cable of resistance 3.5 . If the load across
the secondary winding is 1.8k, determine (a) the primary current
flowing, and (b) the power dissipated in the load resistance.
[(a) 15 A (b) 2.81 kW]
15 An a.c. source of 20
6
0
°
V and internal resistance 10.24 k is
matched to a load for maximum power transfer by a 16:1 ideal
transformer. Determine (a) the value of the load resistance, and
(b) the power dissipated in the load. [(a) 40 (b) 9.77 mW]
Assignment 11
This assignment covers the material in chapters 34 and 35.
The marks for each question are shown in brackets at the end of
each question.
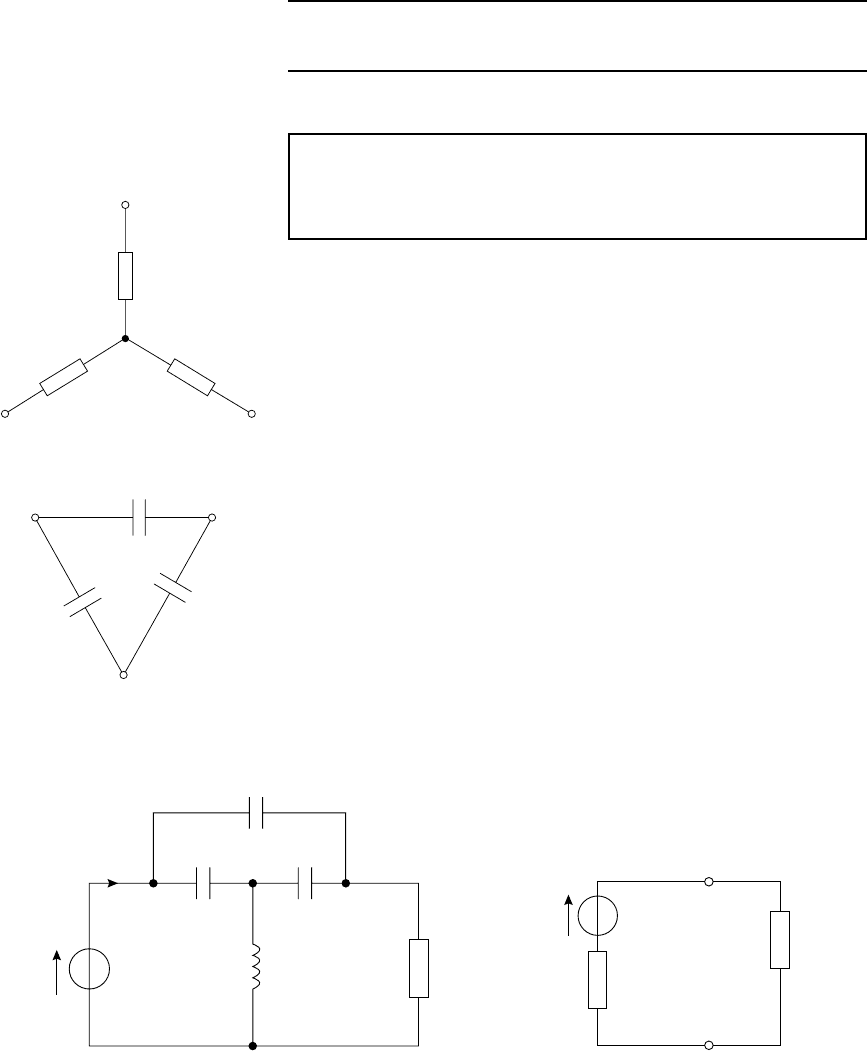
1 Determine the delta-connected equivalent network for the star-
connected impedances shown in Figure A11.1 (9)
(3+j4)Ω
(2−j5)Ω
(1+j)Ω
Figure A11.1
2 Transform the delta-connection in Figure A11.2 to it’s equivalent
star connection. Hence determine for the network shown in
Figure A11.3
(a) the total circuit impedance
(b) the current I
(c) the current in the 20 resistor
(d) the power dissipated in the 20 resistor. (17)
−j40 Ω
−j20 Ω
−j20 Ω
Figure A11.2
3 If the load impedance Z in Figure A11.4 consists of variable resistance
and variable reactance, find (a) the value of Z that results in maximum
power transfer, and (b) the value of the maximum power. (6)
4 Determine the value of the load resistance R in Figure A11.5 that
gives maximum power dissipation and calculate the value of
power. (9)
−j40 Ω
−j20 Ω−j20 Ω
j15 Ω 20 Ω
I
50∠0° V
Figure A11.3
Z
100∠0° V
(4+j3) Ω
Figure A11.4

630 Electrical Circuit Theory and Technology
50 V
10 Ω
40 Ω
R
Figure A11.5
5 An a.c. source of 10
6
0
°
V and internal resistance 5 k is matched to
a load for maximum power transfer by a 5:1 ideal transformer. Deter-
mine (a) the value of the load resistance, and (b) the power dissipated
in the load. (9)

36 Complex Waveforms
At the end of this chapter you should be able to:
ž define a complex wave
ž recognize periodic functions
ž recognize the general equation of a complex waveform
ž use harmonic synthesis to build up a complex wave
ž recognize characteristics of waveforms containing odd, even
or odd and even harmonics, with or without phase change
ž calculate rms and mean values, and form factor of a complex
wave
ž calculate power associated with complex waves
ž perform calculations on single phase circuits containing
harmonics
ž define and perform calculations on harmonic resonance
ž list and explain some sources of harmonics
36.1 Introduction
In preceding chapters a.c. supplies have been assumed to be sinusoidal,
this being a form of alternating quantity commonly encountered in elec-
trical engineering. However, many supply waveforms are not sinusoidal.
For example, sawtooth generators produce ramp waveforms, and rectan-
gular waveforms may be produced by multivibrators. A waveform that
is not sinusoidal is called a complex wave. Such a waveform may be
shown to be composed of the sum of a series of sinusoidal waves having
various interrelated periodic times.
A function ft is said to be periodic if ft C T D ft for all values
of t, where T is the interval between two successive repetitions and is
called the period of the function ft. A sine wave having a period of
2/ω is a familiar example of a periodic function.
A typical complex periodic-voltage waveform, shown in Figure 36.1,
has period T seconds and frequency f hertz. A complex wave such as
this can be resolved into the sum of a number of sinusoidal waveforms,
and each of the sine waves can have a different frequency, amplitude
and phase.
The initial, major sine wave component has a frequency f equal to
the frequency of the complex wave and this frequency is called the
fundamental frequency. The other sine wave components are known
as harmonics, these having frequencies which are integer multiples of
frequency f. Hence the second harmonic has a frequency of 2f, the third
harmonic has a frequency of 3f, and so on. Thus if the fundamental (i.e.,
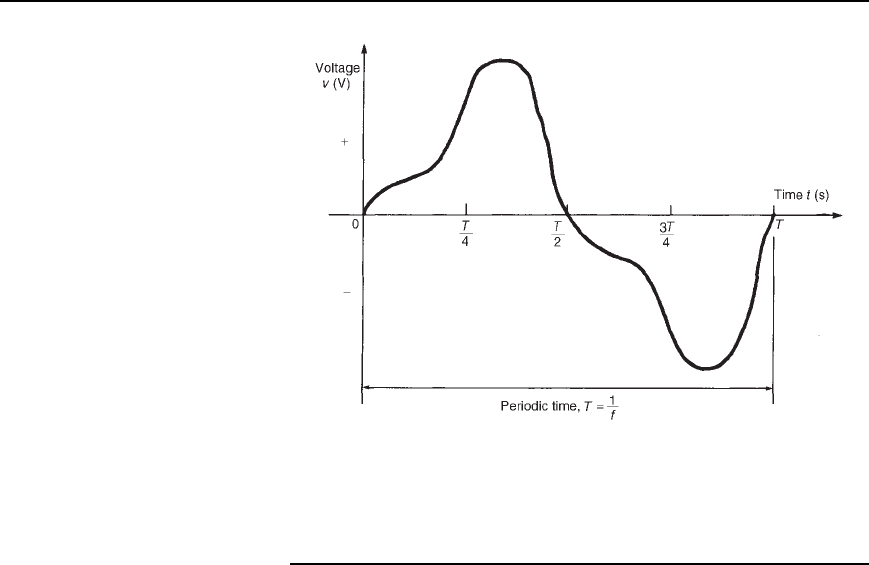
632 Electrical Circuit Theory and Technology
Figure 36.1 Typical complex periodic voltage waveform
supply) frequency of a complex wave is 50 Hz, then the third harmonic
frequency is 150 Hz, the fourth harmonic frequency is 200 Hz, and so on.
36.2 The general
equation for a complex
waveform
The instantaneous value of a complex voltage wave acting in a linear
circuit may be represented by the general equation
v D V
m
sin.!t Y9
1
/ Y V
2m
sin.2!t Y9
2
/
Y
···Y V
nm
sin.n!t Y9
n
/volts 36.1
Here V
1m
sinωt C
1
represents the fundamental component of which
V
1m
is the maximum or peak value, frequency, f D ω/2 and
1
is the
phase angle with respect to time, t D 0.
Similarly, V
2m
sin2ωt C
2
represents the second harmonic compo-
nent, and V
nm
sinnωt C
n
represents the nth harmonic component, of
which V
nm
is the peak value, frequency D nω/2D nf and
n
is the
phase angle.
In the same way, the instantaneous value of a complex current i may
be represented by the general equation
i
= I
1m
sin.!t Y q
1
/ Y I
2m
sin.2!t Y q
2
/
Y
···Y I
nm
sin.n!t Y q
n
/amperes 36.2
Where equations (36.1) and (36.2) refer to the voltage across and the
current flowing through a given linear circuit, the phase angle between
the fundamental voltage and current is
1
D
1
1
, the phase angle
between the second harmonic voltage and current is
2
D
2
2
,and
so on.

Complex Waveforms 633
It often occurs that not all harmonic components are present in a
complex waveform. Sometimes only the fundamental and odd harmonics
are present, and in others only the fundamental and even harmonics are
present.
36.3 Harmonic synthesis
Harmonic analysis is the process of resolving a complex periodic
waveform into a series of sinusoidal components of ascending order of
frequency. Many of the waveforms met in practice can be represented by
mathematical expressions similar to those of equations (36.1) and (36.2),
and the magnitude of their harmonic components together with their
phase may be calculated using Fourier series (see Higher Engineering
Mathematics). Numerical methods are used to analyse waveforms for
which simple mathematical expressions cannot be obtained. A numerical
method of harmonic analysis is explained in Chapter 37. In a laboratory,
waveform analysis may be performed using a waveform analyser
which produces a direct readout of the component waves present in a
complex wave.
By adding the instantaneous values of the fundamental and progressive
harmonics of a complex wave for given instants in time, the shape of a
complex waveform can be gradually built up. This graphical procedure is
known as harmonic synthesis (synthesis meaning ‘the putting together
of parts or elements so as to make up a complex whole’).
A number of examples of harmonic synthesis will now be considered.
Example 1
Consider the complex voltage expression given by
v
a
= 100sin!t Y 30sin3!t volts
The waveform is made up of a fundamental wave of maximum value
100 V and frequency, f D ω/2 hertz and a third harmonic component
of maximum value 30 V and frequency D 3ω/2D 3f, the fundamental
and third harmonics being initially in phase with each other. Since the
maximum value of the third harmonic is 30 V and that of the fundamental
is 100 V, the resultant waveform
a
is said to contain 30/100, i.e., ‘30%
third harmonic’. In Figure 36.2, the fundamental waveform is shown by
the broken line plotted over one cycle, the periodic time being 2/ω
seconds. On the same axis is plotted 30 sin 3ωt, shown by the dotted
line, having a maximum value of 30 V and for which three cycles are
completed in time T seconds. At zero time, 30sin 3ωt is in phase with
100sinωt.
The fundamental and third harmonic are combined by adding ordinates
at intervals to produce the waveform for
v
a
as shown. For example, at
time T/12 seconds, the fundamental has a value of 50 V and the third
harmonic a value of 30 V. Adding gives a value of 80 V for waveform
v
a
,
at time T/12 seconds. Similarly, at time T/4 seconds, the fundamental
has a value of 100 V and the third harmonic a value of 30 V. After
addition, the resultant waveform
v
a
is 70 V at time T/4. The procedure
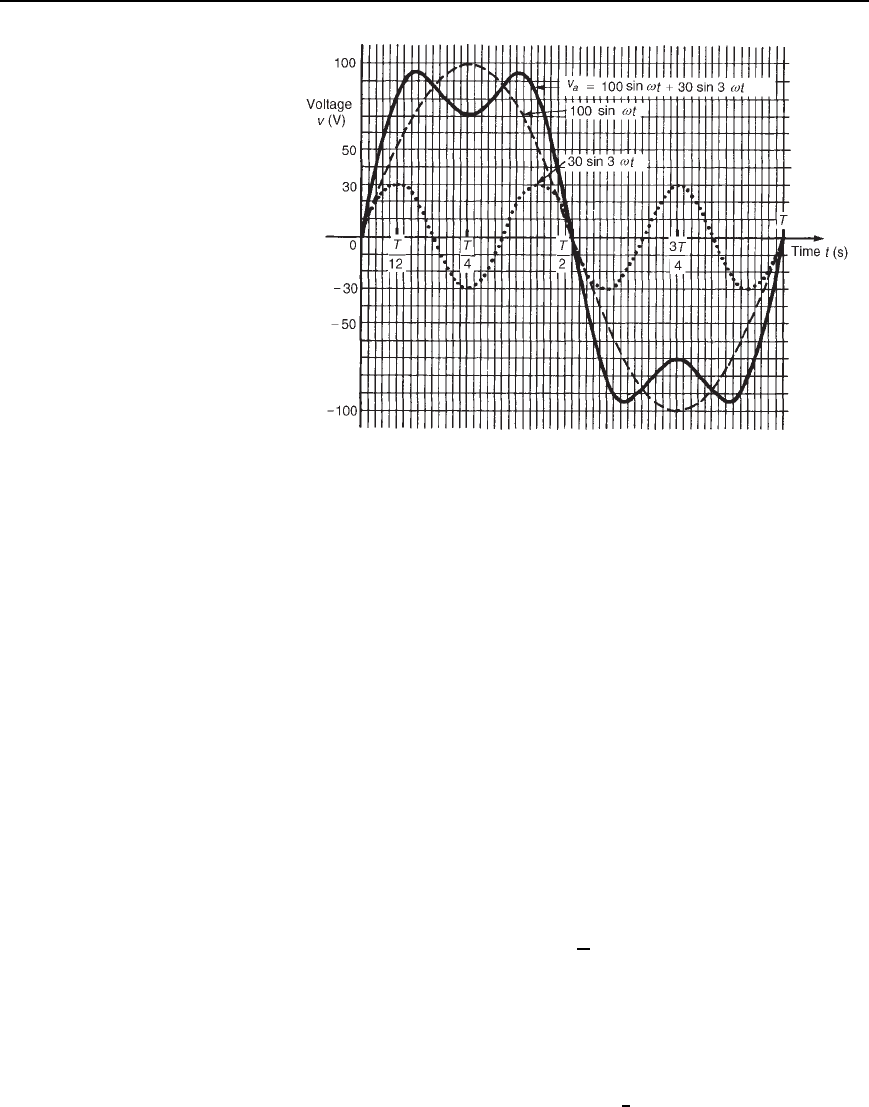
634 Electrical Circuit Theory and Technology
Figure 36.2
is continued between t D 0andt D T to produce the complex waveform
for
v
a
. The negative half-cycle of waveform v
a
is seen to be identical in
shape to the positive half-cycle.
Example 2
Consider the addition of a fifth harmonic component to the complex wave-
form of Figure 36.2, giving a resultant waveform expression
v
b
= 100sin!t Y 30sin3!t Y 20sin5!t volts
Figure 36.3 shows the effect of adding (100sinωt C 30 sin 3ωt) obtained
from Figure 36.2 to 20sin5ωt. The shapes of the negative and positive
half-cycles are still identical. If further odd harmonics of the appropriate
amplitude and phase were added to
v
b
, a good approximation to a square
wave would result.
Example 3
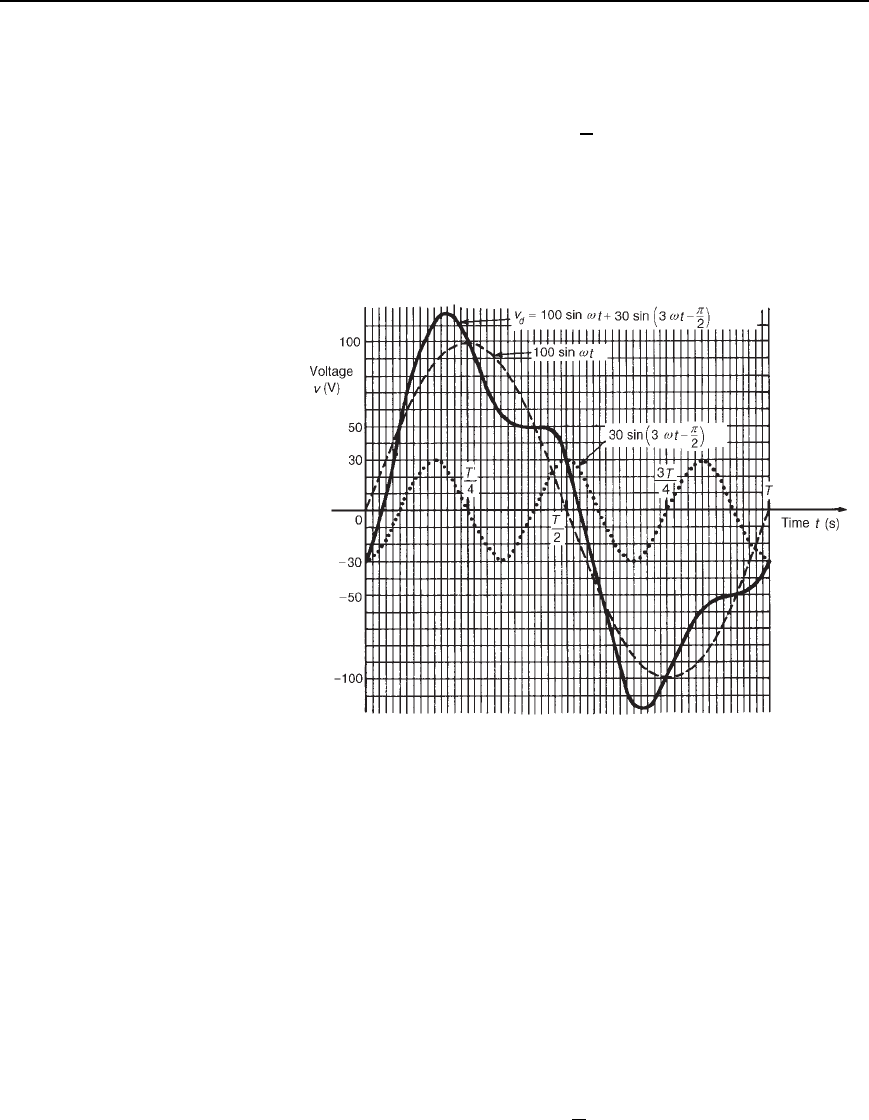
Consider the complex voltage expression given by
v
c
= 100sin!t Y 30sin
3!t Y
p
2
volts
This expression is similar to voltage
v
a
in that the peak value of the
fundamental and third harmonic are the same. However the third harmonic
has a phase displacement of /2 radian leading (i.e., leading 30sin3ωt
by /2 radian). Note that, since the periodic time of the fundamental is
T seconds, the periodic time of the third harmonic is T/3 seconds, and
a phase displacement of /2 radian or
1
4
cycle of the third harmonic
represents a time interval of T/3 ł 4, i.e., T/12 seconds.
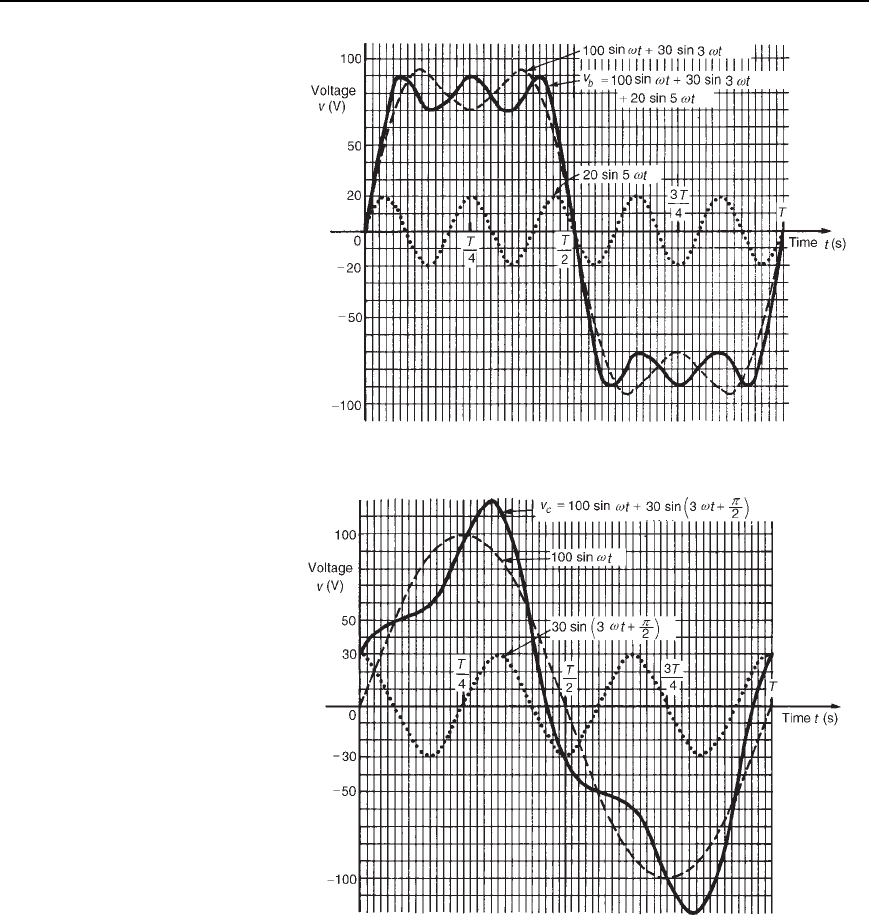
Complex Waveforms 635
Figure 36.3
Figure 36.4
Figure 36.4 shows graphs of 100 sin ωt and 30sin3ωt C /2 over
the time for one cycle of the fundamental. When ordinates of the two
graphs are added at intervals, the resultant waveform
v
c
is as shown. The
shape of the waveform
v
c
is quite different from that of waveform v
a
shown in Figure 36.2, even though the percentage third harmonic is the
same. If the negative half-cycle in Figure 36.4 is reversed it can be seen
that the shape of the positive and negative half-cycles are identical.
636 Electrical Circuit Theory and Technology
Example 4
Consider the complex voltage expression given by
v
d
= 100sin!t Y 30sin
3!t −
p
2
volts
The fundamental, 100 sin ωt, and the third harmonic component,
30sin3ωt /2, are plotted in Figure 36.5, the latter lagging
30sin3ωt by /2 radian or T/12 seconds. Adding ordinates at intervals
gives the resultant waveform
v
d
as shown. The negative half-cycle of v
d
is identical in shape to the positive half-cycle.
Figure 36.5
Example 5
Consider the complex voltage expression given by
v
e
= 100sin!t Y 30sin.3!t Y p/volts
The fundamental, 100 sin ωt, and the third harmonic component,
30sin3ωt C , are plotted as shown in Figure 36.6, the latter leading
30sin3ωt by radian or T/6 seconds. Adding ordinates at intervals
gives the resultant waveform
v
e
as shown. The negative half-cycle of v
e
is identical in shape to the positive half-cycle.
Example 6
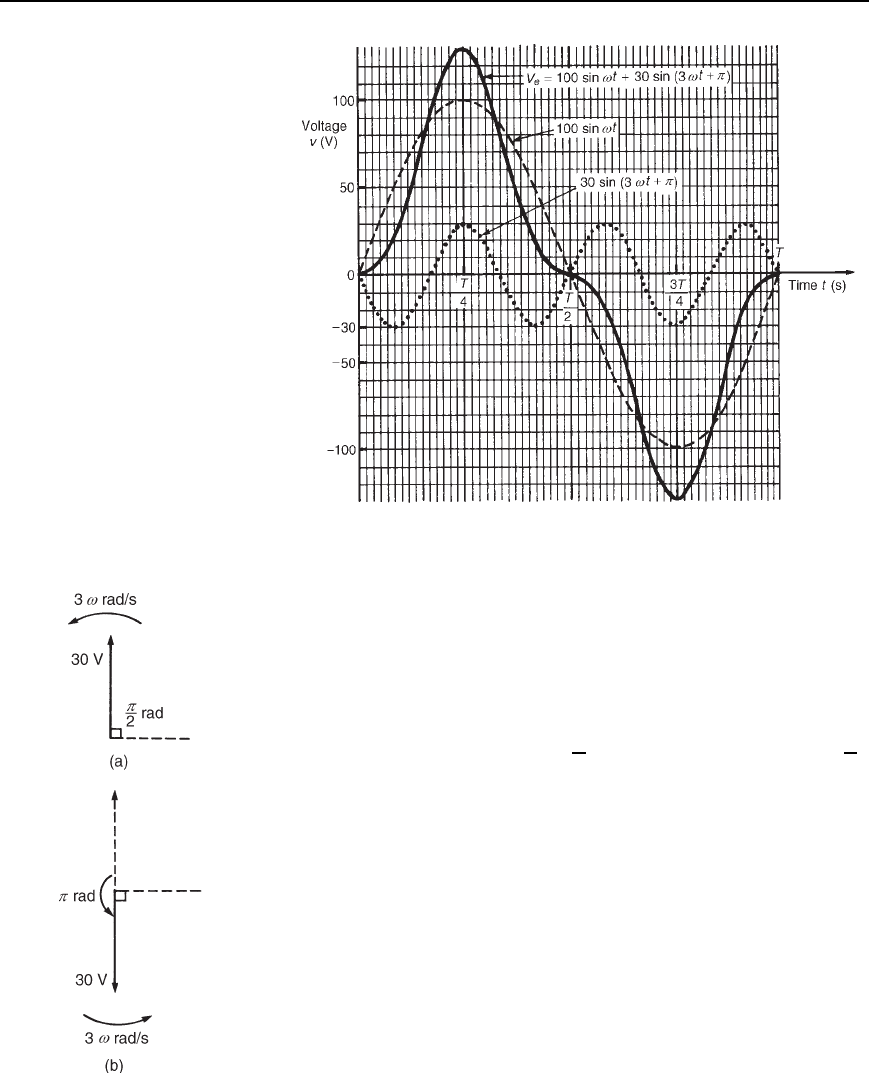
Consider the complex voltage expression given by
v
f
D 100sinωt 30sin
3ωt C
2
volts
Complex Waveforms 637
Figure 36.6
Figure 36.7
The phasor representing 30sin3ωt C /2) is shown in Figure 36.7(a)
at time t D 0. The phasor representing 30sin3ωt C /2) is shown
in Figure 36.7(b) where it is seen to be in the opposite direction to that
shown in Figure 36.7(a).
30sin3ωt C /2) is the same as 30sin3ωt /2). Thus
v
f
D 100sinωt 30sin
3ωt C
2
D 100sinωt C 30sin
3ωt
2
The waveform representing this expression has already been plotted in
Figure 36.5.
General conclusions on examples 1 to 6
Whenever odd harmonics are added to a fundamental waveform, whether
initially in phase with each other or not, the positive and negative half-
cycles of the resultant complex wave are identical in shape (i.e., in
Figures 36.2 to 36.6, the values of voltage in the third quadrant—between
T/2 seconds and 3T/4 seconds—are identical to the voltage values in the
first quadrant—between 0 and T/4 seconds, except that they are negative,
and the values of voltage in the second and fourth quadrants are identical,
except for the sign change). This is a feature of waveforms containing a
fundamental and odd harmonics and is true whether harmonics are added
or subtracted from the fundamental.
