Bird J. Electrical Circuit Theory and Technology

Подождите немного. Документ загружается.

Th´evenin’s and Norton’s theorems 579

Note that, to ﬁnd the current in the capacitor, only the capacitor

need have been initially removed from the circuit. However,

removing each of the components from the branch through

which the current is required will often result in a simpler

solution.

(ii) From Figure 33.13,

current I

200

5000 C 20000

D 8mA

The open-circuit e.m.f. E is equal to the p.d. across the 20 k

resistor, i.e.

E D 8 ð 10

3

20 ð 10

 D 160 V.

(iii) Removing the 200

V source gives the network shown in

Figure 33.14.

Figure 33.14

The impedance, z, ‘looking in’ at the open-circuited terminals

is given by

z D

5 ð 20

5 C 20

k D 4kZ

Figure 33.15

(iv) The Th

evenin equivalent circuit is shown in Figure 33.15,

where current i

is given by

C z

160

150  j120 ð 10

C 4 ð 10

160

195.23 ð 10

37.93

D 0.82

37.93

Thus the current ﬂowing in the capacitor is 0.82 mA.

(b) P.d. across the 150 k resistor,

D i

R D 0.82 ð 10

3

150 ð 10

 D 123 V

Figure 33.16

Problem 2. Determine, for the network shown in Figure 33.16,

the value of current I. Each of the voltage sources has a frequency

of 2 kHz.

(i) The impedance through which current I is ﬂowing is initially

removed from the network, as shown in Figure 33.17.

(ii) From Figure 33.17,

current, I

20  10

2 C 3

D 2A

Figure 33.17

580 Electrical Circuit Theory and Technology

Figure 33.18

Hence the open circuit e.m.f. E D 20  I

2 D 20  22 D 16 V.

(Alternatively, E D 10 C I

3 D 10 C 23 D 16 V.)

(iii) When the sources of e.m.f. are removed from the circuit, the

impedance, z, ‘looking in’ at the break is given by

z D

2 ð 3

2 C 3

D 1.2 Z

(iv) The Th

evenin equivalent circuit is shown in Figure 33.18, where

inductive reactance,

D 2fL D 22000235 ð 10

6

 D 2.95 

Hence current

I D

1.2 C 1.5 Cj2.95

4.0

47.53

D 4.0

−47.53

A or .2.70 − j2.95/ A

Problem 3. Use Th

evenin’s theorem to determine the power dissi-

pated in the 48  resistor of the network shown in Figure 33.19.

Figure 33.19

The power dissipated by a current I ﬂowing through a resistor R is given

by I

R, hence initially the current ﬂowing in the 48  resistor is required.

(i) The 48 C j144 impedance is initially removed from the network

as shown in Figure 33.20.

(ii) From Figure 33.20,

current, i D

300  j400

D 0.1

53.13

Figure 33.20

Hence the open-circuit voltage

E D i300 D 0.1

53.13

300 D 30

53.13

(iii) When the 50

V source shown in Figure 33.20 is removed, the

impedance, z, is given by

z D

j400300

300  j400

400

90

300

500

53.13

D 240

36.87

 or .192 − j144/Z

(iv) The Th

evenin equivalent circuit is shown in Figure 33.21 connected

to the 48 C j144 load.

Current I D

53.13

192  j144 C 48 C j144

53.13

240

D 0.125

53.13

Figure 33.21

Th´evenin’s and Norton’s theorems 581

Hence the power dissipated in the 48 Z resistor

D I

R D 0.125

48 D 0.75 W

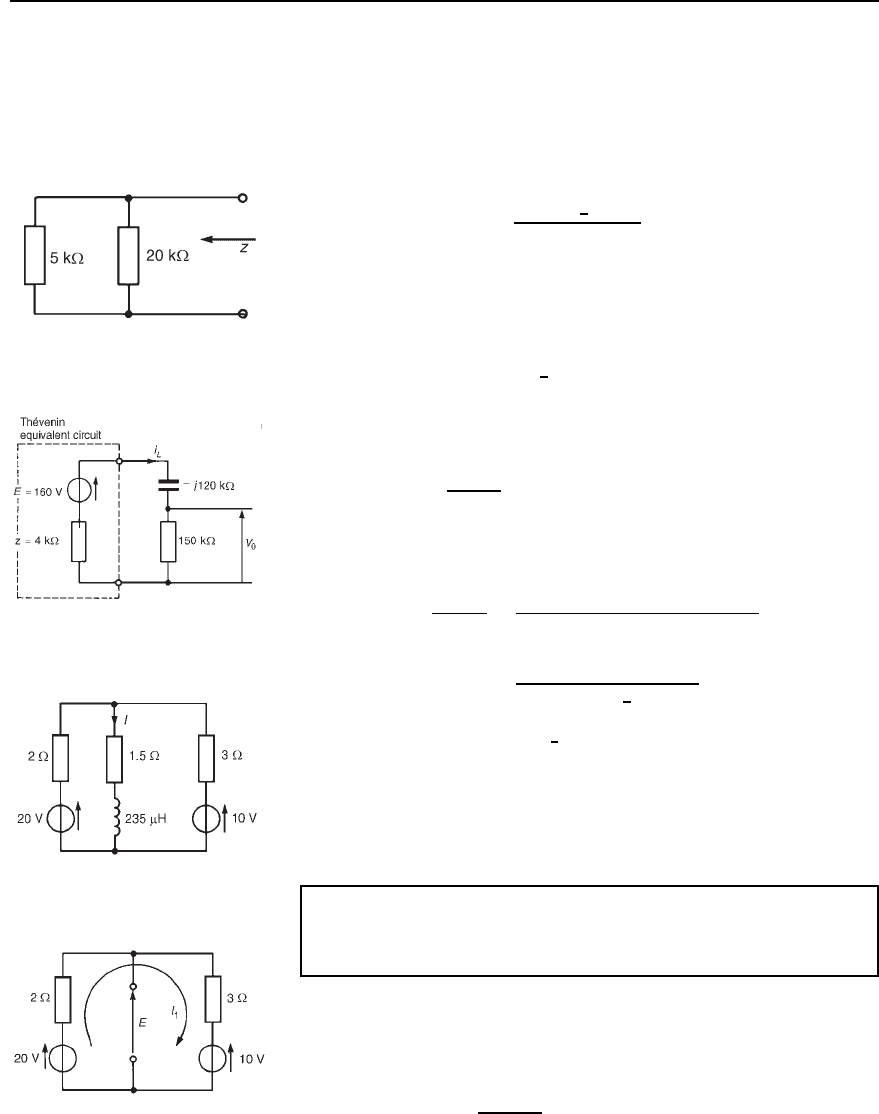
Problem 4. For the network shown in Figure 33.22, use

evenin’s theorem to determine the current ﬂowing in the 80 

resistor.

Figure 33.22

One method of analysing a multi-branch network as shown in

Figure 33.22 is to use Th

evenin’s theorem on one part of the network

at a time. For example, the part of the circuit to the left of AA may be

reduced to a Th

evenin equivalent circuit.

From Figure 33.23,



20 C 5



100 D 80 V, by voltage division

and z

20 ð 5

20 C5

D 4 

Thus the network of Figure 33.22 reduces to that of Figure 33.24. The

part of the network shown in Figure 33.24 to the left of BB may be

reduced to a Th

evenin equivalent circuit, where



50 C 46 C 4



80 D 40 V

Figure 33.23 Figure 33.24

570 Electrical Circuit Theory and Technology

and current I



6 C j8

3 C j4 C 6 C j8



0.062 C j0.964

D 0.041 C j0.643A

(v) If Figure 32.22 is superimposed on Figure 32.20, the resultant

currents are as shown in Figure 32.24.

Figure 32.24

(vi) Resultant current ﬂowing from (5 C j0)V source is given by

C I

D 0.614  j0.025 C 0.041 C j0.643

D .0.573 Y j0.618/A or 0.843

47.16

Resultant current ﬂowing from (2 C j4)V source is given by

C I

D 0.622 C j0.363 C 0.062 C j0.964

D .0.560 Y j1.327/A or 1.440

67.12

Resultant current ﬂowing through the 6 C j8 impedance is

given by

 I

D 0.00731  j0.388  0.0207 C j0.321

D .0.0134

− j0.709/A or 0.709

−88.92

(b) Voltage across 6 C j8 impedance is given by

I

 I

6 C j8 D 0.709

88.92

10

53.13



D 7.09

35.79

i.e., the magnitude of the voltage across the 6 C j8 impedance

is 7.09 V

P D E

I

C I

 cos

C E

I

C I

 cos

where 

is the phase angle between E

and (I

C I

)and

is the

phase angle between E

and (I

C I

), i.e.,

582 Electrical Circuit Theory and Technology

Figure 33.25

and z

50 ð 50

50 C50

D 25 

Thus the original network reduces to that shown in Figure 33.25.

The part of the network shown in Figure 33.25 to the left of CC may be

reduced to a Th

evenin equivalent circuit, where



60 C 25 C 15



40 D 24 V

and z

6040

60 C 40

D 24 

Thus the original network reduces to that of Figure 33.26, from which

the current in the 80 Z resistor is given by

I D



80 C 16 C 24



D 0.20 A

Figure 33.26

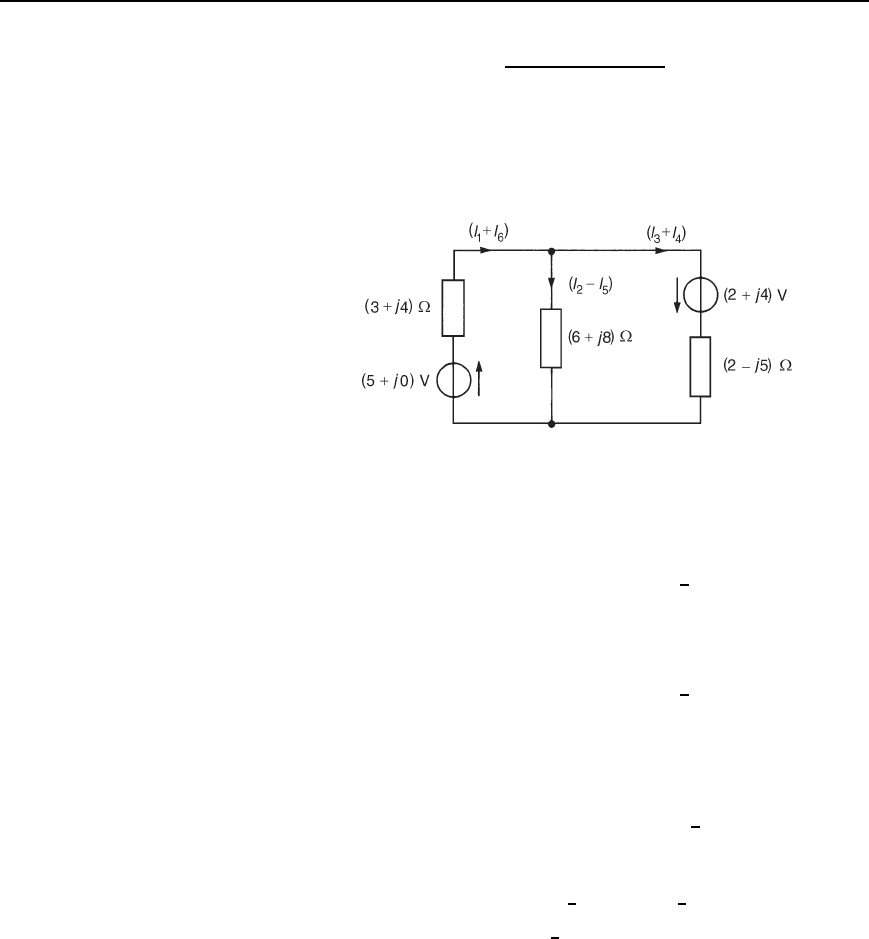
Problem 5. Determine the Th

evenin equivalent circuit with

respect to terminals AB of the circuit shown in Figure 33.27.

Hence determine (a) the magnitude of the current ﬂowing in a

3.75 C j11 impedance connected across terminals AB, and

(b) the magnitude of the p.d. across the 3.75 C j11 impedance.

Figure 33.27

Current I

shown in Figure 33.27 is given by

4 C j3 j3

D 6

The Th

evenin equivalent voltage, i.e., the open-circuit voltage across

terminals AB, is given by

E D I

4 C j3 D 6

5

36.87

 D 30

36.87

When the 24

V source is removed, the impedance z ‘looking in’ at

AB is given by

z D

4 C j3j3

4 C j3 j3

9  j12

D .2.25

− j3.0/Z

Thus the Th

evenin equivalent circuit is as shown in Figure 33.28.

(a) When a 3.75 C j11 impedance is connected across terminals AB,

the current I ﬂowing in the impedance is given by

I D

36.87

3.75 C j11 C 2.25  j3.0

36.87

53.13

D 3

16.26

Th´evenin’s and Norton’s theorems 583

Figure 33.28 Figure 33.29

Hence the current ﬂowing in the .3.75 Y j11/Z impedance

is3A.

(b) P.d. across the 3.75 Cj11 impedance is given by

V D 3

16.26

3.75 C j11 D 3

16.26

11.62

71.18



D 34.86

54.92

Hence the magnitude of the p.d. across the impedance is 34.9 V.

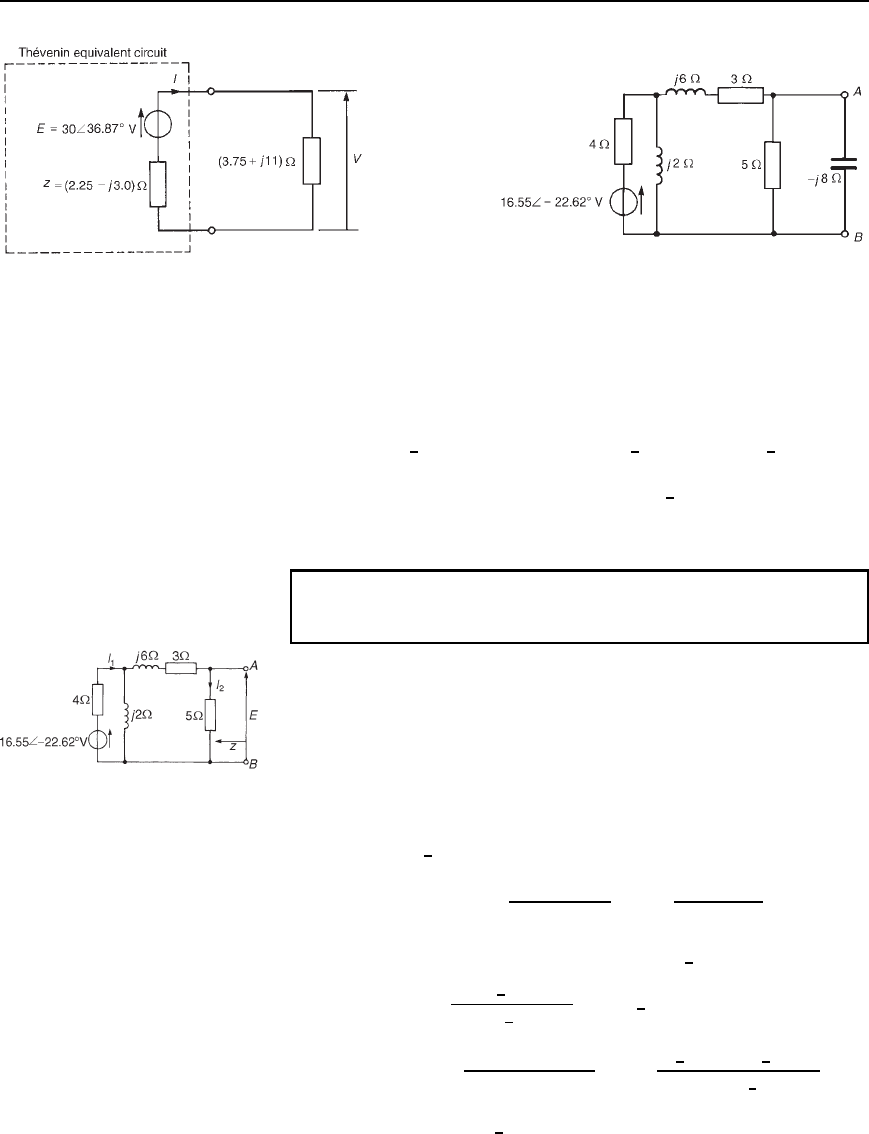
Problem 6. Use Th

evenin’s theorem to determine the current

ﬂowing in the capacitor of the network shown in Figure 33.29.

(i) The capacitor is removed from branch AB, as shown in

Figure 33.30.

(ii) The open-circuit voltage, E, shown in Figure 33.30, is given by

I

5. I

may be determined by current division if I

is known.

(Alternatively, E may be determined by the method used in

problem 4.)

Figure 33.30

Current I

D V/Z, where Z is the total circuit impedance and

V D 16.55

22.62

Impedance, Z D 4 C

j28 Cj6

j2 C 8 C j6

D 4 C

12 C j16

8 C j8

D 4.596

22.38



Hence I

16.55

22.62

4.596

22.38

D 3.60

45

and I



j2 C 3 C j6 C 5



2

3.60

45



11.314

D 0.636

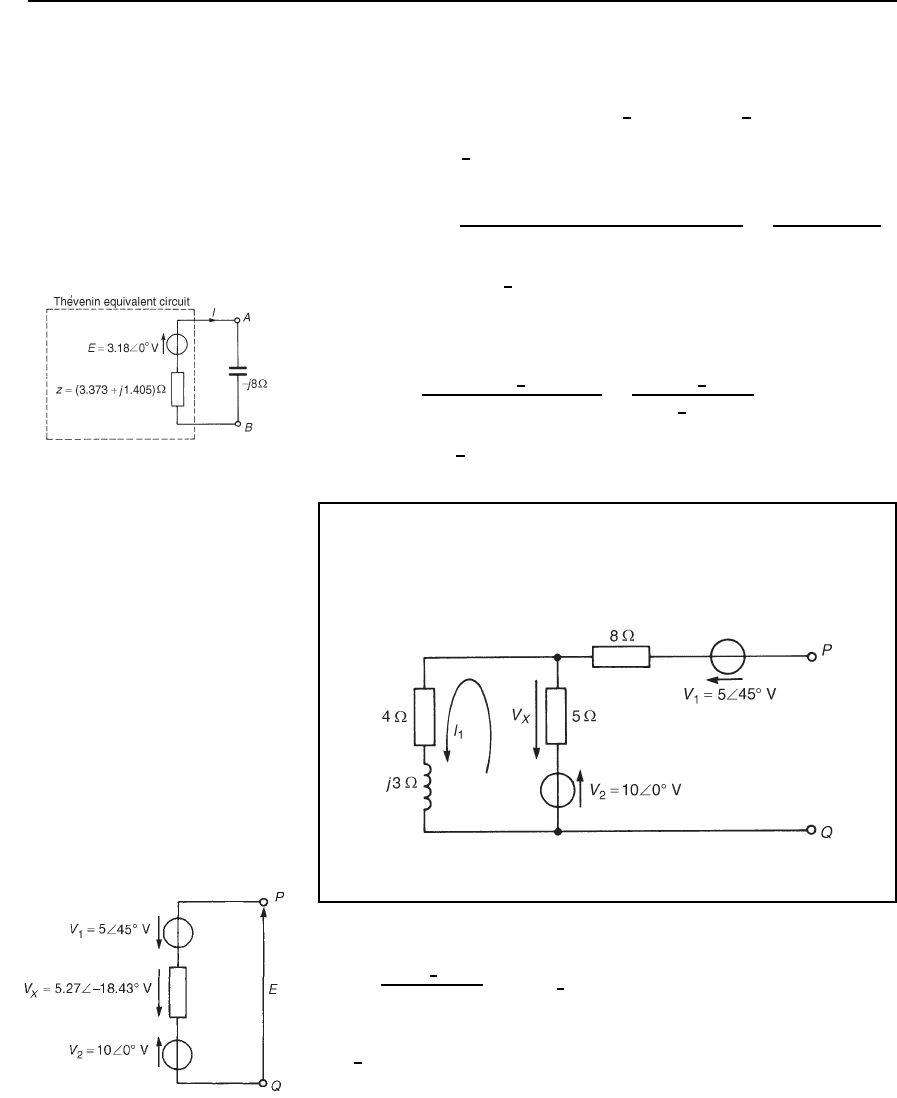
584 Electrical Circuit Theory and Technology

(An alternative method of ﬁnding I

is to use Kirchhoff’s laws or

mesh-current or nodal analysis on Figure 33.30.)

Hence E D I

5 D 0.636

5 D 3.18

(iii) If the 16.55

22.62

V source is removed from Figure 33.30, the

impedance, z, ‘looking in’ at AB is given by

z D

5[4 ðj2/4 C j2 C 3 C j6]

5 C [4 ð j2/4 C j2 C 3 C j6]

53.8 C j7.6

8.8 C j7.6

i.e. z D 3.654

22.61

 or .3.373 Y j1.405/Z

(iv) The Th

evenin equivalent circuit is shown in Figure 33.31, where

the current ﬂowing in the capacitor, I, is given by

I D

3.18

3.373 C j1.405  j8

3.18

7.408

62.91

D 0.43

62.91

A in the direction from A to B

Figure 33.31

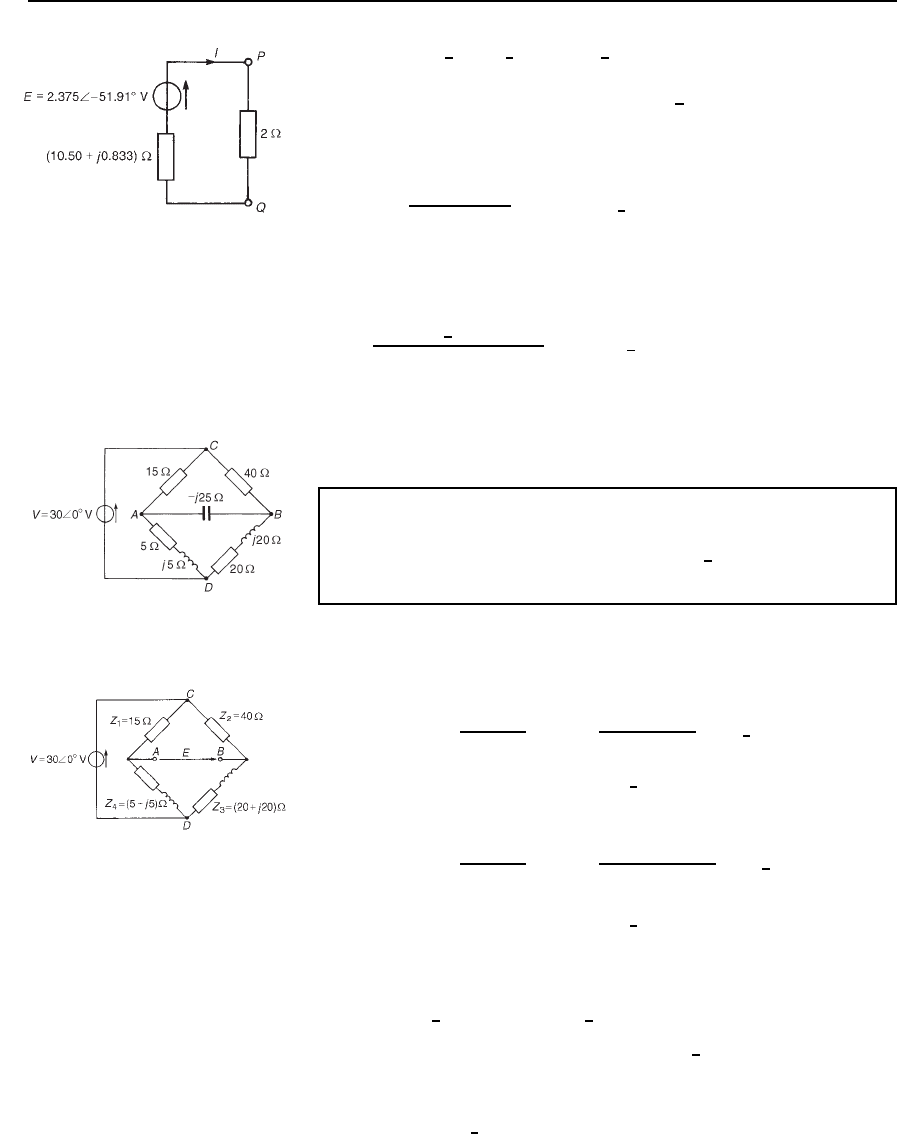
Problem 7. For the network shown in Figure 33.32, derive the

evenin equivalent circuit with respect to terminals PQ, and

hence determine the power dissipated by a 2  resistor connected

across PQ.

Figure 33.32

Current I

shown in Figure 33.32 is given by

5 C 4 Cj3

D 1.054

18.43

Hence the voltage drop across the 5  resistor is given by V

D I

5 D

5.27

18.43

V, and is in the direction shown in Figure 33.32, i.e., the

direction opposite to that in which I

is ﬂowing.

The open-circuit voltage E across PQ is the phasor sum of V

, V

and

, as shown in Figure 33.33.

Figure 33.33

Th´evenin’s and Norton’s theorems 585

Figure 33.34

Thus E D 10

 5

 5.27

18.43

D 1.465  j1.869Vor2.375

−51.91

The impedance, z, ‘looking in’ at terminals PQ with the voltage sources

removed is given by

z D 8 C

54 C j3

5 C 4 Cj3

D 8 C2.635

18.44

D .10.50 Y j0.833/Z

The Th

evenin equivalent circuit is shown in Figure 33.34 with the 2 

resistance connected across terminals PQ.

The current ﬂowing in the 2  resistance is given by

I D

2.375

51.91

10.50 C j0.833 C 2

D 0.1896

55.72

The power P dissipated in the 2  resistor is given by

P D I

R D 0.1896

2 D 0.0719 W  72 mW, correct to two

signiﬁcant ﬁgures.

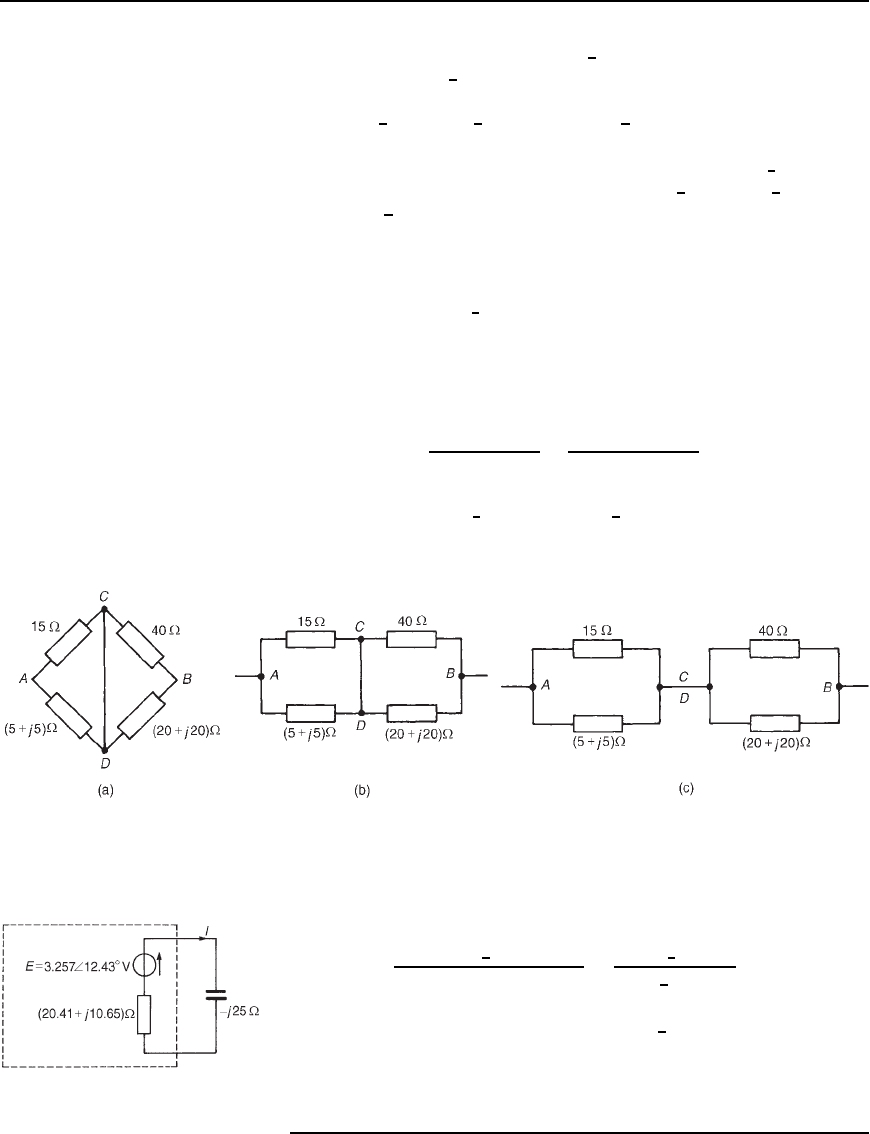
Problem 8. For the a.c. bridge network shown in Figure 33.35,

determine the current ﬂowing in the capacitor, and its direction,

by using Th

evenin’s theorem. Assume the 30

V source to have

negligible internal impedance.

Figure 33.35

(i) The j25  capacitor is initially removed from the network, as

shown in Figure 33.36.

(ii) P.d. between A and C,



C Z



V D



15 C 5 C j5



30



D 21.83

14.04

Figure 33.36

P.d. between B and C,



C Z



V D



40 C 20 C j20



30



D 18.97

18.43

Assuming that point A is at a higher potential than point B, then

the p.d. between A and B is

21.83

 14.04

 18.97

18.43

D 3.181 C j0.701Vor3.257

12.43

i.e., the open-circuit voltage across AB is given by

E D 3.257

12.43

586 Electrical Circuit Theory and Technology

Point C is at a potential of 30

V. Between C and A is a volt

drop of 21.83

14.04

V. Hence the voltage at point A is

 21.83

14.04

D 10.29

30.98

Between points C and B is a voltage drop of 18.97

18.43

Hence the voltage at point B is 30

 18.97

18.43

13.42

26.55

Since the magnitude of the voltage at B is higher than at A, current

must ﬂow in the direction B to A.

(iii) Replacing the 30

V source with a short-circuit (i.e., zero internal

impedance) gives the network shown in Figure 33.37(a). The

network is shown redrawn in Figure 33.37(b) and simpliﬁed in

Figure 33.37(c). Hence the impedance, z, ‘looking in’ at terminals

AB is given by

z D

155 C j5

15 C 5 Cj5

4020 C j20

40 C 20 C j20

D 5.145

30.96

C 17.889

26.57

i.e., z D 20.41 C j10.65

Figure 33.37

(iv) The Th

evenin equivalent circuit is shown in Figure 33.38, where

current I is given by

I D

3.257

12.43

20.41 C j10.65  j25

3.257

12.43

24.95

35.11

D 0.131

47.54

Thus a current of 131 mA ﬂows in the capacitor in a direction

fromBtoA.

Figure 33.38

Th´evenin’s and Norton’s theorems 587

Further problems on Th´evenin’s theorem may be found in Section 33.5,

problems 1 to 10, page 598.

33.3 Norton’s theorem

A source of electrical energy can be represented by a source of e.m.f. in

series with an impedance. In Section 33.2, the Th

evenin constant-voltage

source consisted of a constant e.m.f. E, which may be alternating or direct,

in series with an internal impedance, z. However, this is not the only form

of representation. A source of electrical energy can also be represented by

a constant-current source, which may be alternating or direct, in parallel

with an impedance. It is shown in Section 33.4 that the two forms are in

fact equivalent.

Norton’s theorem states:

‘The current that ﬂows in any branch ofa network is the same as that which

would ﬂow in the branch if it were connected across a source of electrical

energy, the short-circuit current of which is equal to the current that would

ﬂow in a short-circuit across the branch, and the internal impedance of

which is equal to the impedance which appears across the open-circuited

branch terminals.’

The above statement simply means that any linear active network

with output terminals AB, as shown in Figure 33.39(a), can be replaced

by a current source in parallel with an impedance z as shown in

Figure 33.39(b). The equivalent current source I

(note the symbol in

Figure 33.39(b) as per BS 3939:1985) is the current through a short-circuit

applied to the terminals of the network. The impedance z is the equivalent

impedance of the network at the terminals AB when all internal sources of

e.m.f. are made zero. Figure 33.39(b) is known as the Norton equivalent

circuit, and was initially introduced in Section 13.7, page 181 for d.c.

networks.

Figure 33.39 The Norton

equivalent circuit

The following four-step procedure may be adopted when determining

the current ﬂowing in an impedance Z

of a branch AB of an active

network, using Norton’s theorem:

(i) short-circuit branch AB;

(ii) determine the short-circuit current I

;

(iii) remove each source of e.m.f. and replace it by its internal impedance

(or, if a current source exists, replace with an open circuit), then

determine the impedance, z, ‘looking in’ at a break made between

A and B;

(iv) determine the value of the current i

ﬂowing in impedance Z

from

the Norton equivalent network shown in Figure 33.40, i.e.,



C z



Figure 33.40

A simple d.c. network (Figure 33.41) serves to demonstrate how the above

procedure is applied to determine the current ﬂowing in the 5  resistance

by using Norton’s theorem:

Figure 33.41