Bird J. Electrical Circuit Theory and Technology

Подождите немного. Документ загружается.

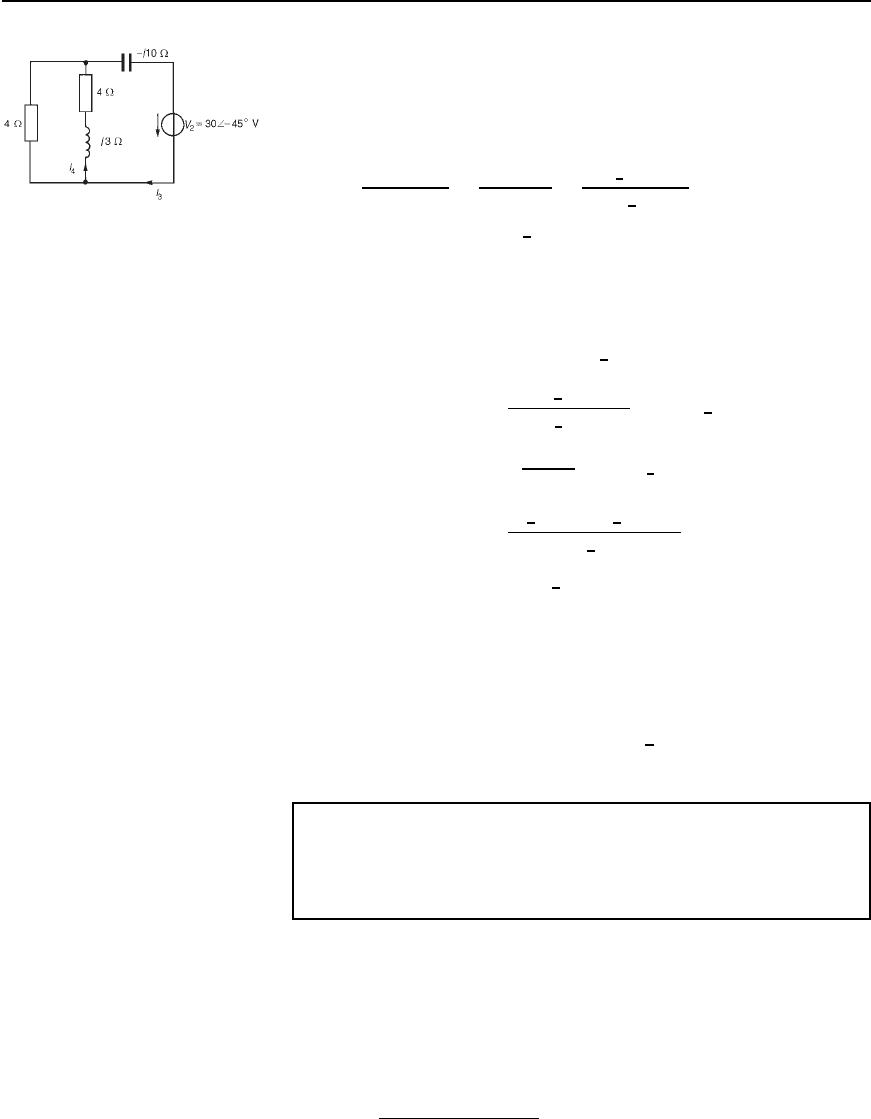
568 Electrical Circuit Theory and Technology

Figure 32.18

(iii) The original network is redrawn with V

removed, as shown in

Figure 32.18.

(iv) Currents I

and I

are shown in Figure 32.18. From Figure 32.18,

4  in parallel with 4 Cj3 gives an equivalent impedance of

44 C j3

4 C 4 C j3

16 C j12

8 C j3

36.87

8.544

20.56

D 2.341

16.31

 or 2.247 Cj0.657

Total impedance of Figure 32.18 is

2.247 C j0.657  j10 D 2.247  j9.343 or

9.609

76.48



Hence current I

45

9.609

76.48

D 3.122

31.48

and current I



8 C j3



3.122

31.48



4

3.122

31.48



8.544

20.56

D 1.462

10.92

Aor1.436 Cj0.277A

(v) If the network of Figure 32.18 is superimposed on the network

of Figure 32.17, it can be seen that the current in the 4 Cj3

impedance is given by I

 I

(vi) I

 I

D 3.588 C j0.692  1.436 C j0.277

D .2.152 Y j0.415/A or 2.192

10.92

ﬂowing from AtoBin Figure 32.16.

Problem 4. For the a.c. network shown in Figure 32.19 determine,

using the superposition theorem, (a) the current in each branch,

(b) the magnitude of the voltage across the 6 Cj8 impedance,

and (c) the total active power delivered to the network.

(a) (i) The original network is redrawn with E

removed, as shown in

Figure 32.20.

(ii) Currents I

, I

and I

are labelled as shown in Figure 32.20.

From Figure 32.20, 6 C j8 in parallel with 2  j5 gives

an equivalent impedance of

6 C j82  j5

6 C j8 C 2  j5

D 5.123  j3.671

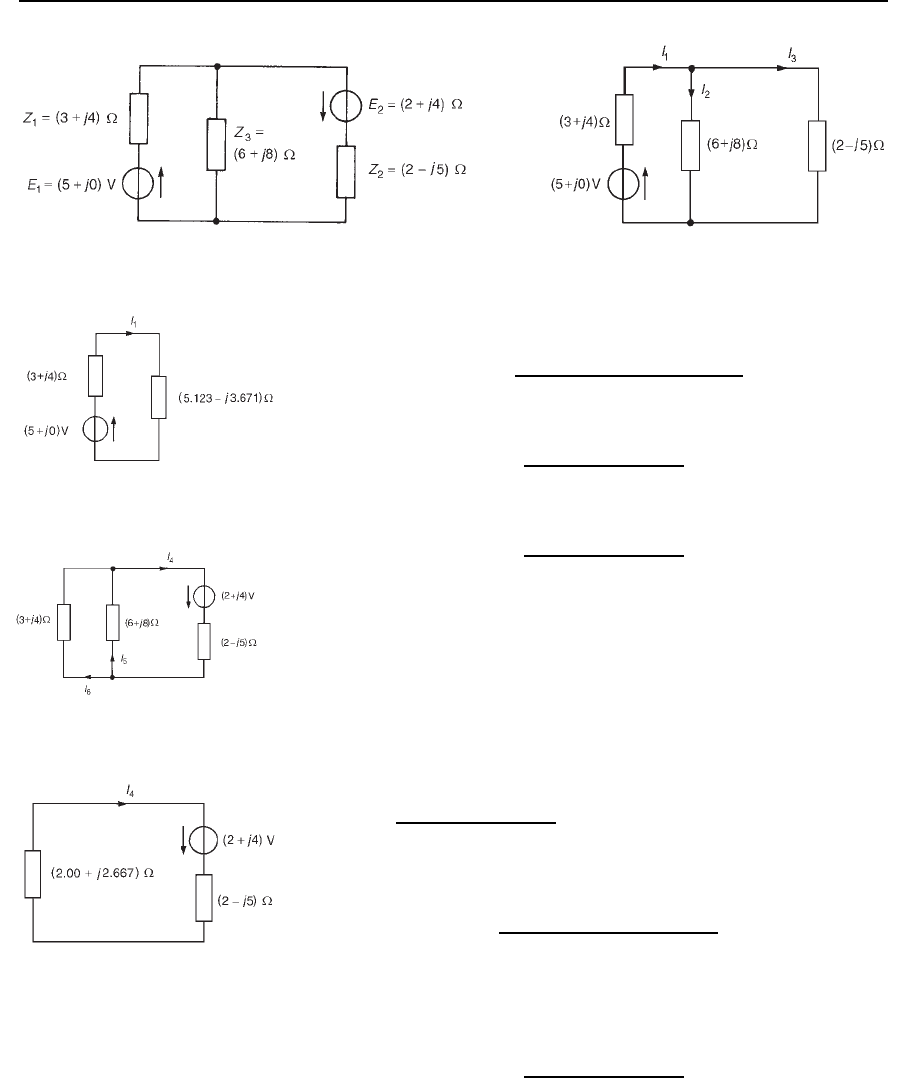
The superposition theorem 569

Figure 32.19 Figure 32.20

From the equivalent network of Figure 32.21,

current I

5 C j0

3 C j4 C 5.123  j3.671

D 0.614  j0.025A

current I



2  j5

6 C j8 C 2  j5



0.614  j0.025

D 0.00731  j0.388A

and current I



6 C j8

6 C j8 C 2  j5



0.614  j0.025

D 0.622 C j0.363A

Figure 32.21

(iii) The original network is redrawn with E

removed, as shown in

Figure 32.22.

Figure 32.22

(iv) Currents I

, I

and I

are shown labelled in Figure 32.22 with I

ﬂowing away from the positive terminal of the 2 C j4V source.

From Figure 32.22, 3 C j4 in parallel with 6 C j8 gives

an equivalent impedance of

3 C j46 C j8

3 C j4 C 6 C j8

D 2.00 C j2.667

From the equivalent network of Figure 32.23,

current I

2 C j4

2.00 C j2.667 C 2  j5

D 0.062 C j0.964A

Figure 32.23

From Figure 32.22,

current I



3 C j4

3 C j4 C 6 C j8



0.062 C j0.964

D 0.0207 C j0.321A

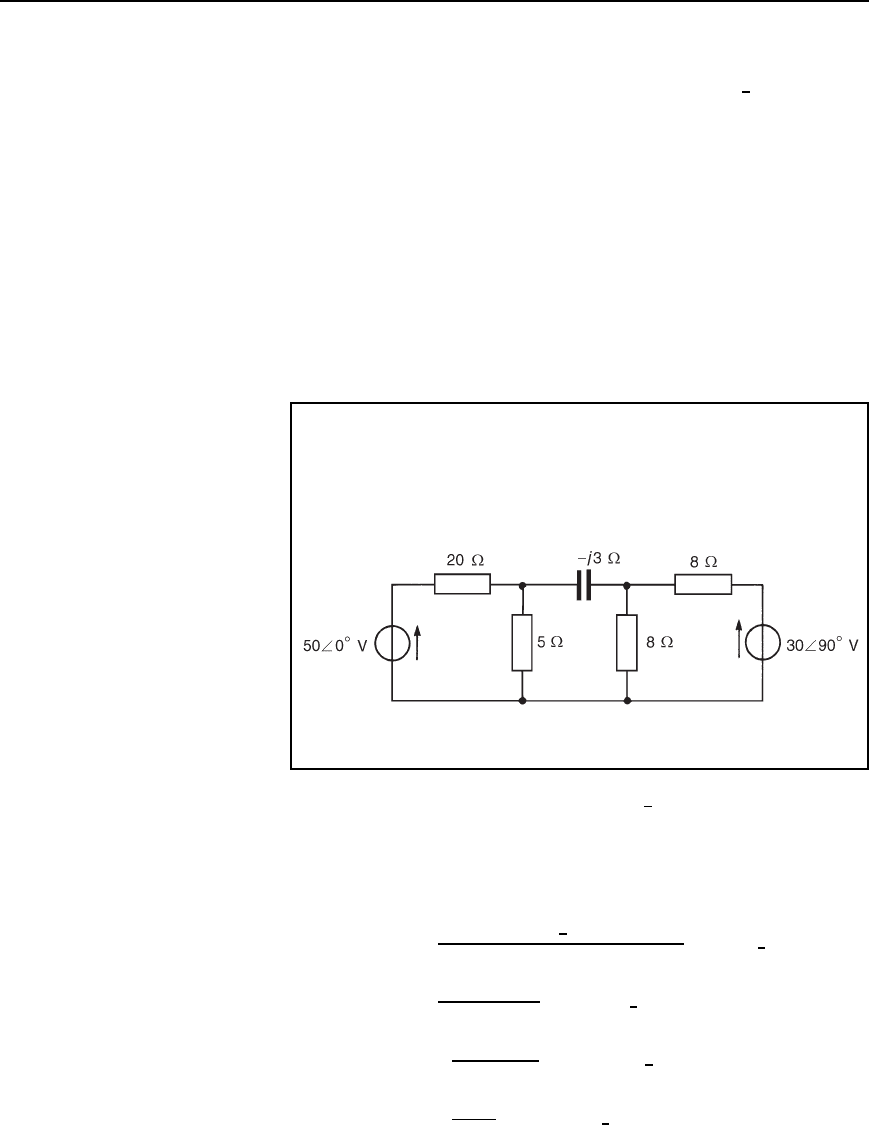
The superposition theorem 571

P D 50.843 cos47.16

 0



C 



2

C 4

1.440 cos



67.12

 arctan



D 2.866 C 6.427 D 9.293 W

D 9.3W, correct to one dec. place.

(This value may be checked since total active power dissipated is

given by:

P D I

C I



3 C I

 I



6 C I

C I



2

D 0.843

3 C 0.709

6 C 1.440

2

D 2.132 C 3.016 C 4.147 D 9.295 W

D 9.3W,correct to one dec. place.

Problem 5. Use the superposition theorem to determine, for the

network shown in Figure 32.25, (a) the magnitude of the current

ﬂowing in the capacitor, (b) the p.d. across the 5  resistance,

total active power taken from the supply.

Figure 32.25

(i) The network is redrawn with the 30

V source removed, as

shown in Figure 32.26.

(ii) Currents I

to I

are shown labelled in Figure 32.26. From

Figure 32.26, two 8  resistors in parallel give an equivalent

resistance of 4 .

Hence I

20 C 54  j3/5 C 4 j3

D 2.220

2.12

4  j3

5 C 4 j3

D 1.170

16.32



5 C 4  j3



D 1.170

20.55



8 C 8



D 0.585

20.55

A D I

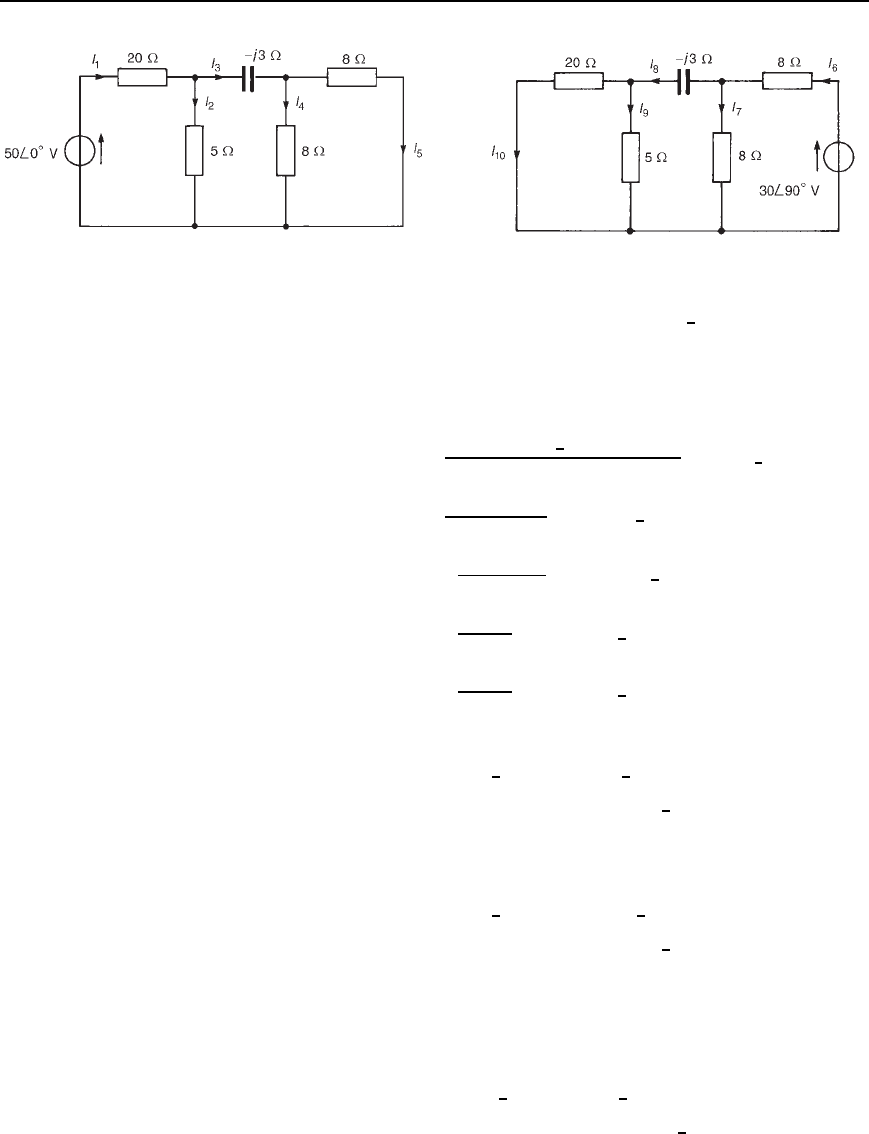
572 Electrical Circuit Theory and Technology

Figure 32.26 Figure 32.27

(iii) The original network is redrawn with the 50

V source removed,

as shown in Figure 32.27.

(iv) Currents I

to I

are shown labelled in Figure 32.27. From

Figure 32.27, 20  in parallel with 5  gives an equivalent

resistance of 20 ð5/20 C 5 D 4 .

Hence I

8 C 84  j3/8 C 4 j3

D 2.715

96.52

4  j3

8 C 4 j3

D 1.097

73.69



8 C 4  j3



D 1.756

110.56



20 C 5



D 1.405

110.56

and I



20 C 5



D 0.351

110.56

(a) The current ﬂowing in the capacitor is given by

I

 I

 D 1.170

20.55

 1.756

110.56

D 1.712  j1.233Aor2.11

35.76

i.e., the magnitude of the current in the capacitor is 2.11 A

(b) The p.d. across the 5  resistance is given by (I

C I

) (5).

I

C I

 D 1.170

16.32

C 1.405

110.56

D 0.629 C j0.987Aor1.17

57.49

Hence the magnitude of the pd. across the 5 Z resistance is

1.175 D 5.85 V

I

 I



20.

I

 I

 D 2.220

2.12

 0.351

110.56

D 2.342  j0.247Aor2.355

6.02

The superposition theorem 573

Hence the active power dissipated in the 20 Z resistance is

2.355

20 D 111 W

(d) Active power developed by the 50

V source

D VI

 I

 cos

D 502.355 cos6.02

 0



D 117.1W

Active power developed by 30

90 V source,

D 30I

 I

 cos

I

 I

 D 2.715

96.52

 0.585

20.55

D 0.856 C j2.492Aor2.635

108.96

Hence P

D 302.635 cos108.96

 90

 D 74.8W.

Total power developed, P D P

C P

D 117.1 C 74.8 D 191.9W

(This value may be checked by summing the I

R powers dissipated

in the four resistors.)

Further problems on the superposition theorem may be found in

Section 32.3 following, problems 1 to 8.

32.3 Further problems

on the superposition

theorem

1 Repeat problems 1, 5, 8 and 9 on page 542, of Chapter 30, and prob-

lems 3, 5 and 13 on page 559, of Chapter 31, using the superposition

theorem.

2 Two batteries each of e.m.f. 15 V are connected in parallel to supply

a load of resistance 2.0 . The internal resistances of the batteries

are 0.5  and 0.3 . Determine, using the superposition theorem, the

current in the load and the current supplied by each battery.

[6.86 A; 2.57 A; 4.29 A]

3 Use the superposition theorem to determine the magnitude of the

current ﬂowing in the capacitive branch of the network shown in

Figure 32.28. [2.584 A]

4 A.c. sources of 20

V and internal resistance 10  and 30

and internal resistance 12  are connected in parallel across an 8 

load. Use the superposition theorem to determine (a) the current in

the 8  load, and (b) the current in each voltage source.

[(a) 1.30 A (b) 20

V source discharges at

1.58

120.98

A, 30

V source

discharges at 1.90

16.49

5 Use the superposition theorem to determine current I

ﬂowing in the

5  resistance of the network shown in Figure 32.29.

[0.529

5.71

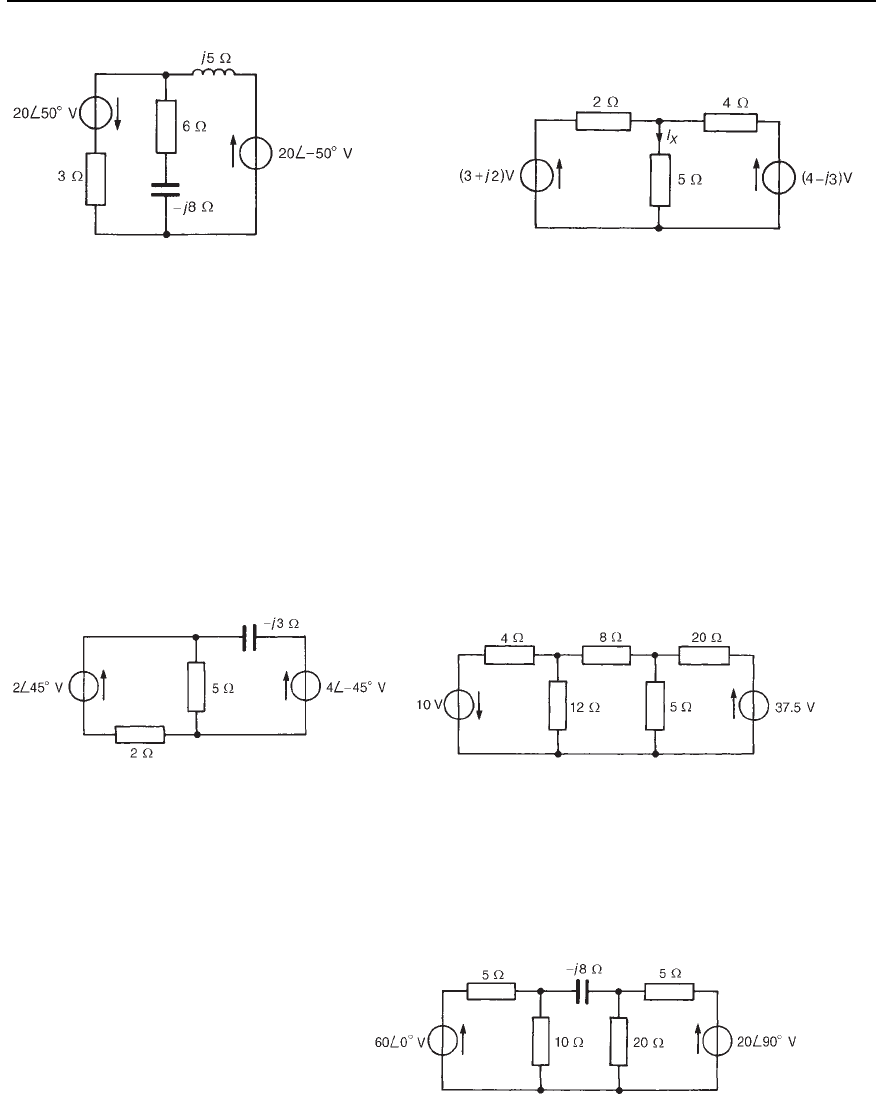
574 Electrical Circuit Theory and Technology

Figure 32.28 Figure 32.29

6 For the network shown in Figure 32.30, determine, using the superpo-

sition theorem, (a) the current ﬂowing in the capacitor, (b) the current

ﬂowing in the 2  resistance, (c) the p.d. across the 5  resistance,

and (d) the total active circuit power.

[(a) 1.28 A (b) 0.74 A (c) 3.01 V (d) 2.91 W]

7 (a) Use the superposition theorem to determine the current in the

12  resistance of the network shown in Figure 32.31. Deter-

mine also the p.d. across the 8  resistance and the power

dissipated in the 20  resistance.

(b) If the 37.5 V source in Figure 32.31 is reversed in direction,

determine the current in the 12  resistance.

[(a) 0.375 A, 8.0 V, 57.8 W (b) 0.625 A]

Figure 32.30 Figure 32.31

8 For the network shown in Figure 32.32, use the superposition theorem

to determine (a) the current in the capacitor, (b) the pd. across the

10  resistance, (c) the active power dissipated in the 20  resistance,

and (d) the total active circuit power.

[(a) 3.97 A (b) 28.7 V (c) 36.4 W (d) 371.6 W]

Figure 32.32

33 Th

evenin’s and

Norton’s theorems

At the end of this chapter you should be able to:

ž understand and use Th

evenin’s theorem to analyse a.c. and

d.c. networks

ž understand and use Norton’s theorem to analyse a.c. and d.c.

networks

ž appreciate and use the equivalence of Th

evenin and Norton

networks

33.1 Introduction

Many of the networks analysed in Chapters 30, 31 and 32 using

Kirchhoff’s laws, mesh-current and nodal analysis and the superposition

theorem can be analysed more quickly and easily by using Th

evenin’s

or Norton’s theorems. Each of these theorems involves replacing what

may be a complicated network of sources and linear impedances with a

simple equivalent circuit. A set procedure may be followed when using

each theorem, the procedures themselves requiring a knowledge of basic

circuit theory. (It may be worth checking some general d.c. circuit theory

in Section 13.4. page 174, before proceeding)

33.2 Th

evenin’s theorem

evenin’s theorem states:

‘The current which ﬂows in any branch of a network is the same as that

which would ﬂow in the branch if it were connected across a source of

electrical energy, the e.m.f. of which is equal to the potential difference

which would appear across the branch if it were open-circuited, and the

internal impedance of which is equal to the impedance which appears

across the open-circuited branch terminals when all sources are replaced

by their internal impedances.’

The theorem applies to any linear active network (‘linear’ meaning that the

measured values of circuit components are independent of the direction

and magnitude of the current ﬂowing in them, and ‘active’ meaning that

it contains a source, or sources, of e.m.f.)

The above statement of Th

evenin’s theorem simply means that

a complicated network with output terminals AB, as shown in

Figure 33.1(a), can be replaced by a single voltage source E in series

with an impedance z, as shown in Figure 33.1(b). E is the open-circuit

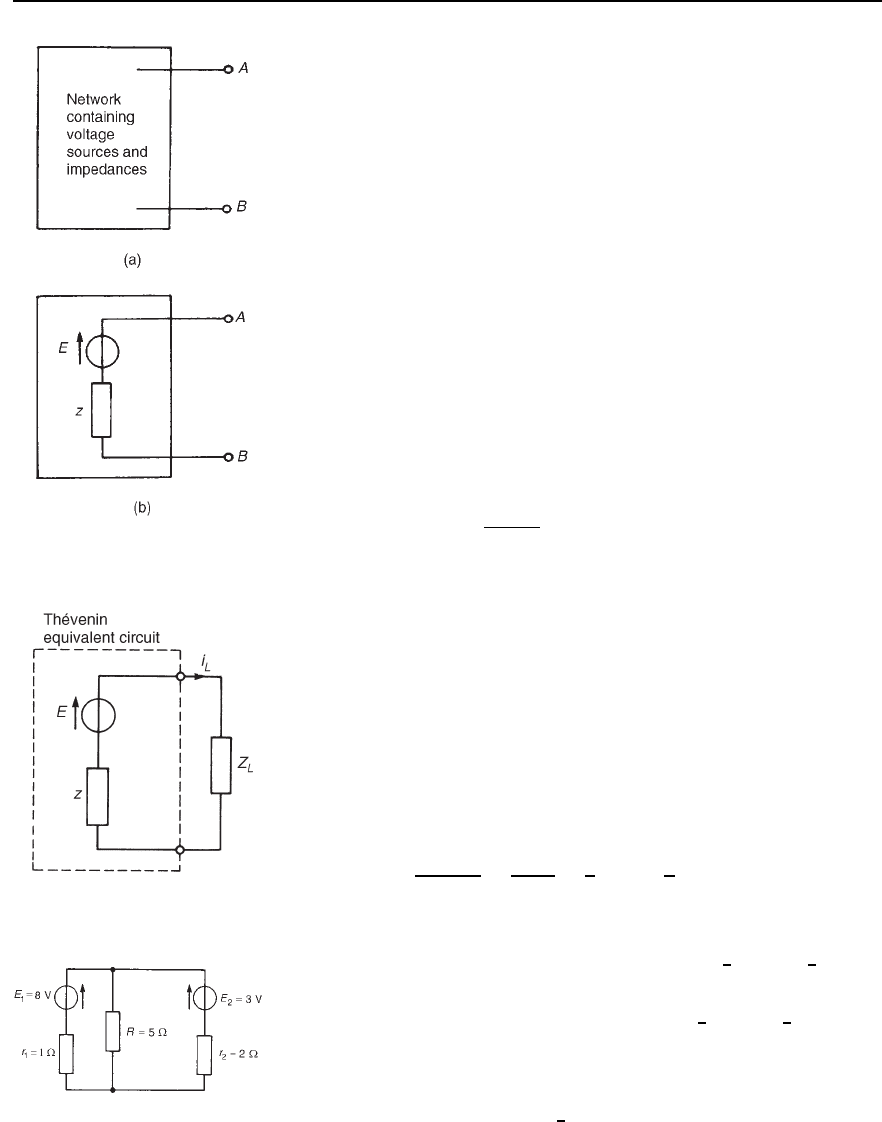
576 Electrical Circuit Theory and Technology

Figure 33.1 The Th´evenin

equivalent circuit

voltage measured at terminals AB and z is the equivalent impedance of

the network at the terminals AB when all internal sources of e.m.f. are

made zero. The polarity of voltage E is chosen so that the current ﬂowing

through an impedance connected between A and B will have the same

direction as would result if the impedance had been connected between A

and B of the original network. Figure 33.1(b) is known as the Th

evenin

equivalent circuit, and was initially introduced in Section 13.4, page 174

for d.c. networks.

The following four-step procedure can be adopted when determining,

by means of Th

evenin’s theorem, the current ﬂowing in a branch

containing impedance Z

of an active network:

(i) remove the impedance Z

from that branch;

(ii) determine the open-circuit voltage E across the break;

(iii) remove each source of e.m.f. and replace it by its internal impedance

(if it has zero internal impedance then replace it by a short-

circuit), and then determine the internal impedance, z, ‘looking in’

at the break;

(iv) determine the current from the Th

evenin equivalent circuit shown

in Figure 33.2, i.e.

current i

Y z

A simple d.c. network (Figure 33.3) serves to demonstrate how the above

procedure is applied to determine the current ﬂowing in the 5  resis-

tance by using Th

evenin’s theorem. This is the same network as used in

Chapter 30 when it was solved using Kirchhoff’s laws (see page 535),

and by means of the superposition theorem in Chapter 32 (see page 562).

A comparison of methods may be made.

Using the above procedure:

(i) the 5  resistor is removed, as shown in Figure 33.4(a).

(ii) The open-circuit voltage E across the break is now required. The

network of Figure 33.4(a) is redrawn for convenience as shown in

Figure 33.4(b), where current,

 E

C r

8  3

1 C 2

or 1

Figure 33.2

Hence the open-circuit voltage E is given by

E D E

 I

i.e., E D 8 





1 D 6

(Alternatively, E D E

 I

r

D 3 C





2 D 6

V.

(iii) Removing each source of e.m.f. gives the network of Figure 33.5.

The impedance, z, ‘looking in’ at the break AB is given by

z D 1 ð2/1 C 2 D



Figure 33.3

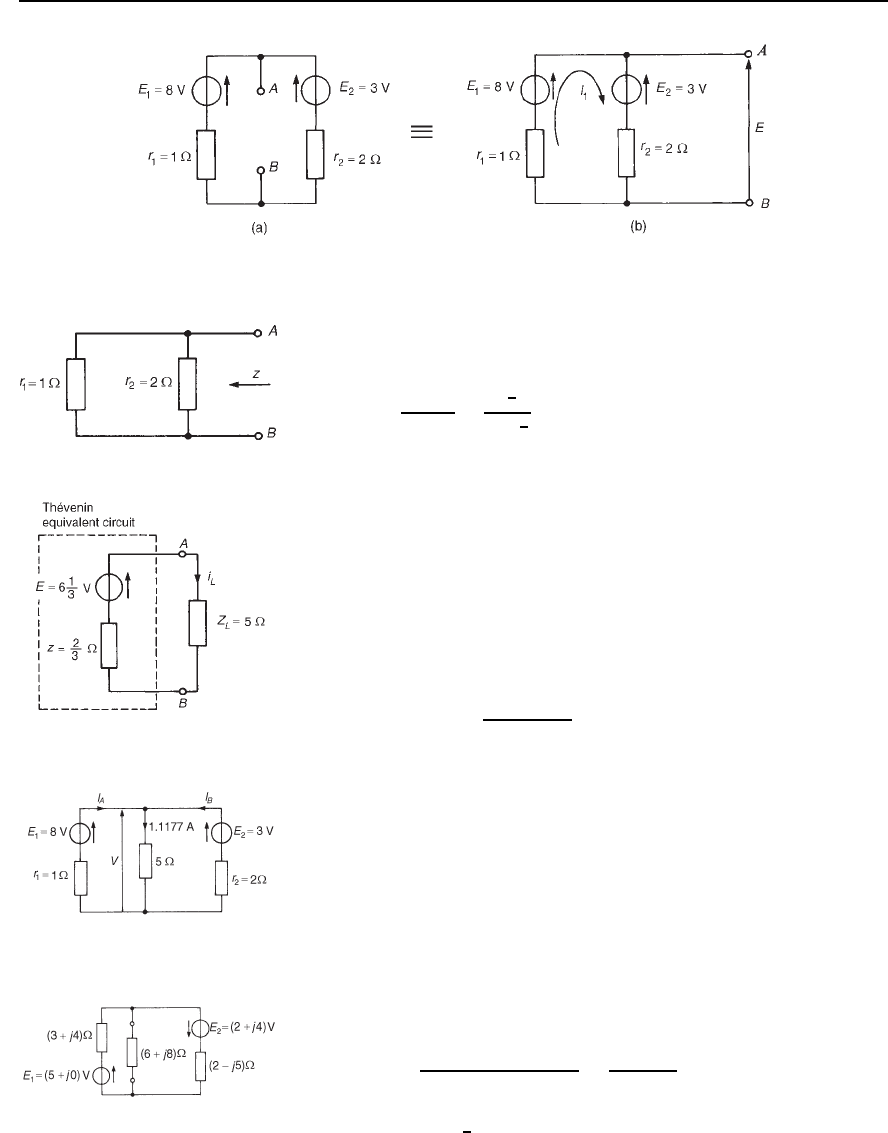
Th´evenin’s and Norton’s theorems 577

Figure 33.4

(iv) The Th

evenin equivalent circuit is shown in Figure 33.6, where

current i

is given by

C z

5 C

D 1.1177

D 1.12 A, correct to two decimal places

Figure 33.5

To determine the currents ﬂowing in the other two branches of

the circuit of Figure 33.3, basic circuit theory is used. Thus, from

Figure 33.7, voltage V D 1.11775 D 5.5885 V.

Then V D E

 I

, i.e., 5.5885 D 8  I

1, from which

current I

D 8  5.5885 D 2.41 A.

Similarly, V D E

 I

, i.e., 5.5885 D 3  I

2, from which

current I

3  5.5885

−1.29 A

Figure 33.6

(i.e., ﬂowing in the direction opposite to that shown in Figure 33.7).

The Th

evenin theorem procedure used above may be applied to a.c. as

well as d.c. networks, as shown below.

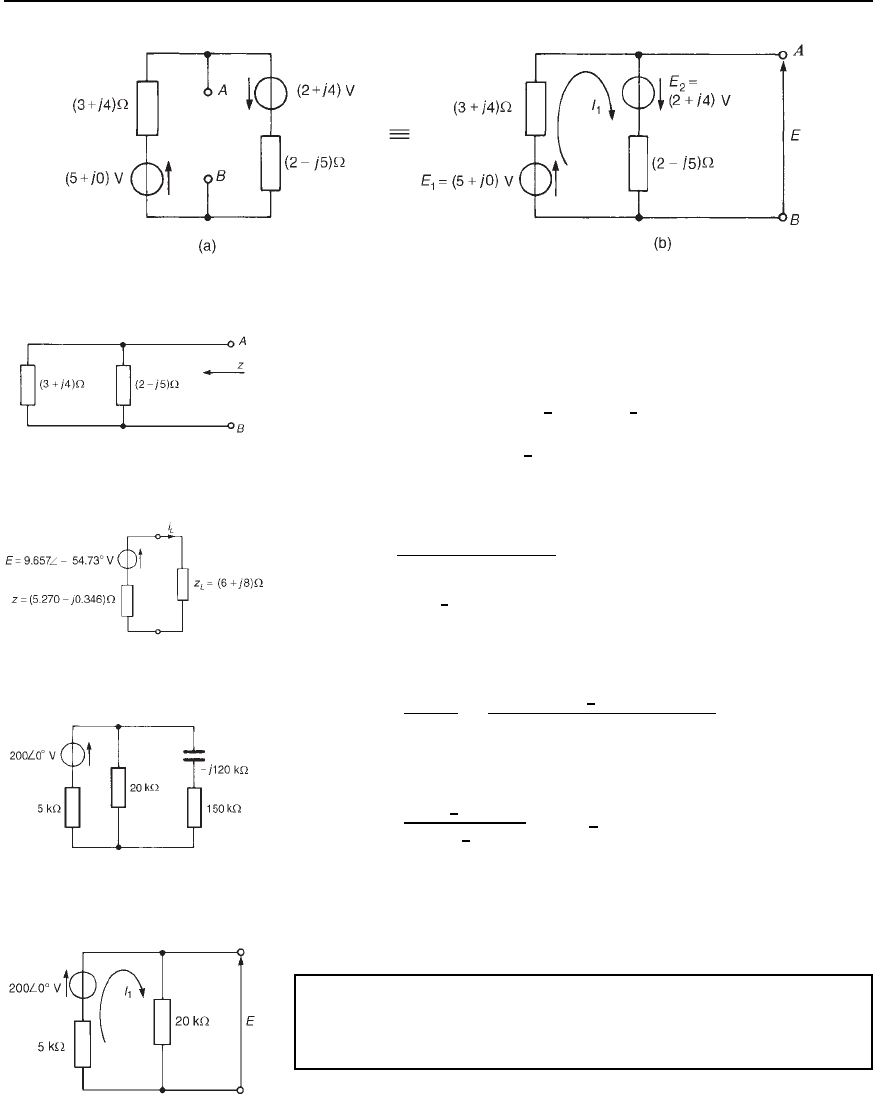
An a.c. network is shown in Figure 33.8 where it is required to ﬁnd the

current ﬂowing in the 6 C j8 impedance by using Th

evenin’s theorem.

Figure 33.7

Using the above procedure

(i) The 6 C j8 impedance is removed, as shown in Figure 33.9(a).

(ii) The open-circuit voltage across the break is now required. The

network is redrawn for convenience as shown in Figure 33.9(b),

where current

5 C j0 C 2 C j4

3 C j4 C 2  j5

7 C j4

5  j

D 1.581

41.05

Figure 33.8

578 Electrical Circuit Theory and Technology

Figure 33.9

Hence open-circuit voltage across AB,

E D E

 I

3 C j4, i.e.,

E D 5 C j0  1.581

41.05

5

53.13



from which E D 9.567

54.73

Figure 33.10

(iii) From Figure 33.10, the impedance z ‘looking in’ at terminals AB

is given by

z D

3 C j42  j5

3 C j4 C 2  j5

D 5.281

3.76

 or 5.270 j0.346

(iv) The Th

evenin equivalent circuit is shown in Figure 33.11, from

which current

C z

9.657

54.73

6 C j8 C 5.270  j0.346

Figure 33.11

Thus, current in 6 C j8 impedance,

9.657

54.73

13.623

34.18

D 0.71

−88.91

The network of Figure 33.8 is analysed using Kirchhoff’s laws in

problem 3, page 539, and by the superposition theorem in problem 4,

page 568. The above analysis using Th

evenin’s theorem is seen to be

much quicker.

Figure 33.12

Problem 1. For the circuit shown in Figure 33.12, use Th

evenin’s

theorem to determine (a) the current ﬂowing in the capacitor, and

(b) the p.d. across the 150 k resistor.

(a) (i) Initially the 150  j120k impedance is removed from the

circuit as shown in Figure 33.13.

Figure 33.13