Bird J. Electrical Circuit Theory and Technology
Подождите немного. Документ загружается.

588 Electrical Circuit Theory and Technology
Figure 33.42
(i) The 5 branch is short-circuited, as shown in Figure 33.42.
(ii) From Figure 33.42, I
SC
D I
1
C I
2
D
8
1
C
3
2
D 9.5A
(iii) If each source of e.m.f. is removed the impedance ‘looking in’ at
a break made between A and B is given by z D 1 ð 2/1 C2 D
2
3
.
(iv) From the Norton equivalent network shown in Figure 33.43, the
current in the 5 resistance is given by I
L
D
2
3
5 C
2
3
9.5 D
1.12 A, as obtained previously using Kirchhoff’s laws, the super-
position theorem and by Th
´
evenin’s theorem.
As with Th
´
evenin’s theorem, Norton’s theorem may be used with a.c.
as well as d.c. networks, as shown below.
An a.c. network is shown in Figure 33.44 where it is required to find the
current flowing in the 6 C j8 impedance by using Norton’s theorem.
Using the above procedure:
Figure 33.43 Figure 33.44
(i) Initially the 6 C j8 impedance is short-circuited, as shown in
Figure 33.45.
(ii) From Figure 33.45,
I
SC
D I
1
C I
2
D
5 C j0
3 C j4
C
2 C j4
2 j5
D 1
6
53.13
°
4.472
6
63.43
°
5.385
6
68.20
°
D 1.152 j1.421Aor1.829
66
−50.97
°
A
Figure 33.45
(iii) If each source of e.m.f. is removed, the impedance, z, ‘looking in’
at a break made between A and B is given by
z D
3 C j42 j5
3 C j4 C 2 j5
D 5.28
66
−3.76
°
Z or .5.269 − j0.346/Z
(iv) From the Norton equivalent network shown in Figure 33.46, the
current is given by
Figure 33.46

Th´evenin’s and Norton’s theorems 589
Figure 33.47 Figure 33.48 Figure 33.49
i
L
D
z
Z
L
C z
I
SC
D
5.28
6
3.76
°
6 C j8 C 5.269 j0.346
1.829
6
50.97
°
i.e., current in .6 Y j8/Z impedance, i
L
= 0.71
66
−88.91
°
A
Problem 9. Use Norton’s theorem to determine the value of
current I in the circuit shown in Figure 33.47.
(i) The branch containing the 2.8 resistor is short-circuited, as shown
in Figure 33.48.
(ii) The 3 resistor in parallel with a short-circuit is the same
as 3 in parallel with 0 giving an equivalent impedance of
3 ð 0/3 C 0 D 0. Hence the network reduces to that shown in
Figure 33.49, where I
SC
D 5/2 D 2.5A.
(iii) If the 5 V source is removed from the network the input impedance,
z, ‘looking-in’ at a break made in AB of Figure 33.48 gives
z D 2 ð 3/2 C 3 D 1.2 Z (see Figure 33.50).
Figure 33.50
Figure 33.51
(iv) The Norton equivalent network is shown in Figure 33.51, where
current I is given by
I D
1.2
1.2 C2.8 j3
2.5 D
3
4 j3
D 0.60
66
36.87
°
A
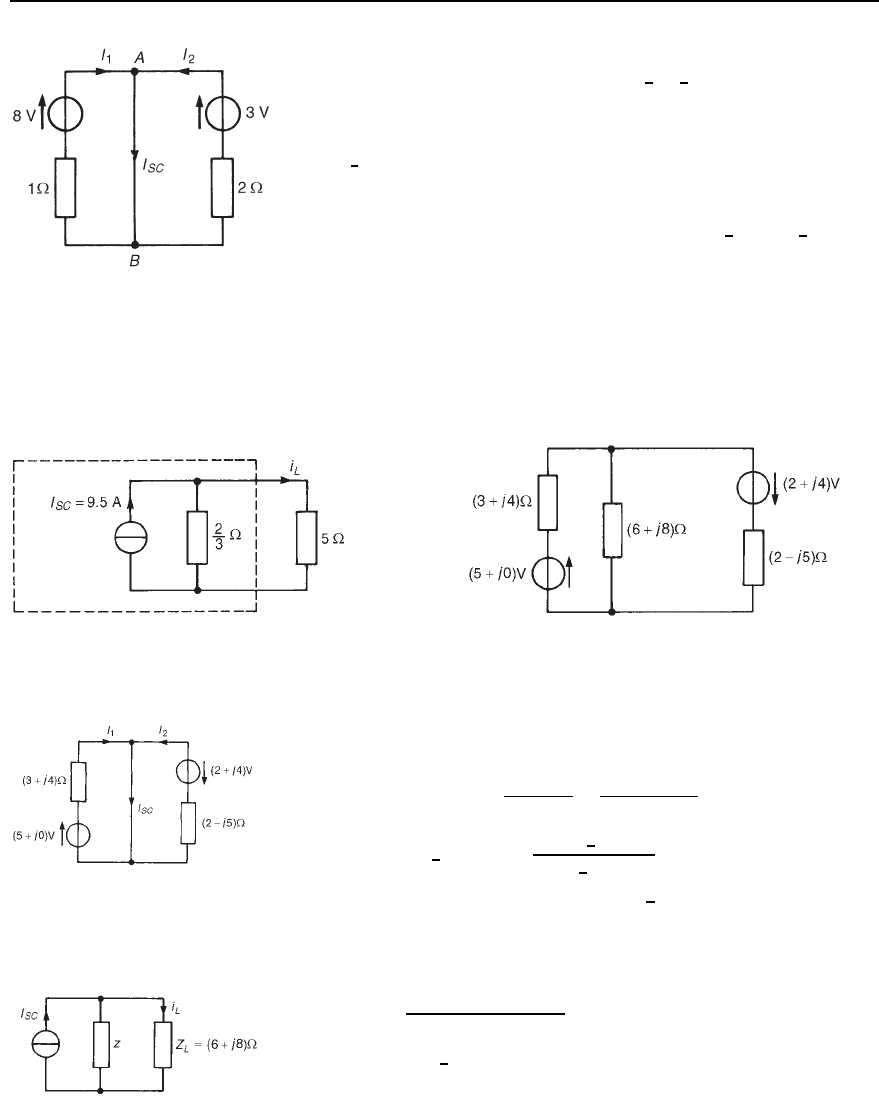
Problem 10. For the circuit shown in Figure 33.52 determine the
current flowing in the inductive branch by using Norton’s theorem.
Figure 33.52
(i) The inductive branch is initially short-circuited, as shown in
Figure 33.53.
(ii) From Figure 33.53,
I
SC
D I
1
C I
2
D
20
2
C
10
3
D 13.
˙
3A
Figure 33.53
590 Electrical Circuit Theory and Technology
Figure 33.54
(iii) If the voltage sources are removed, the impedance, z, ‘looking in’
at a break made in AB is given by z D 2 ð 3/2 C 3 D 1.2 Z.
(iv) The Norton equivalent network is shown in Figure 33.54, where
current I is given by
I D
1.2
1.2 C1.5 C j2.95
13.
P
3 D
16
2.7 C j2.95
D 4.0
66
−47.53
°
A or .2.7 − j2.95/A
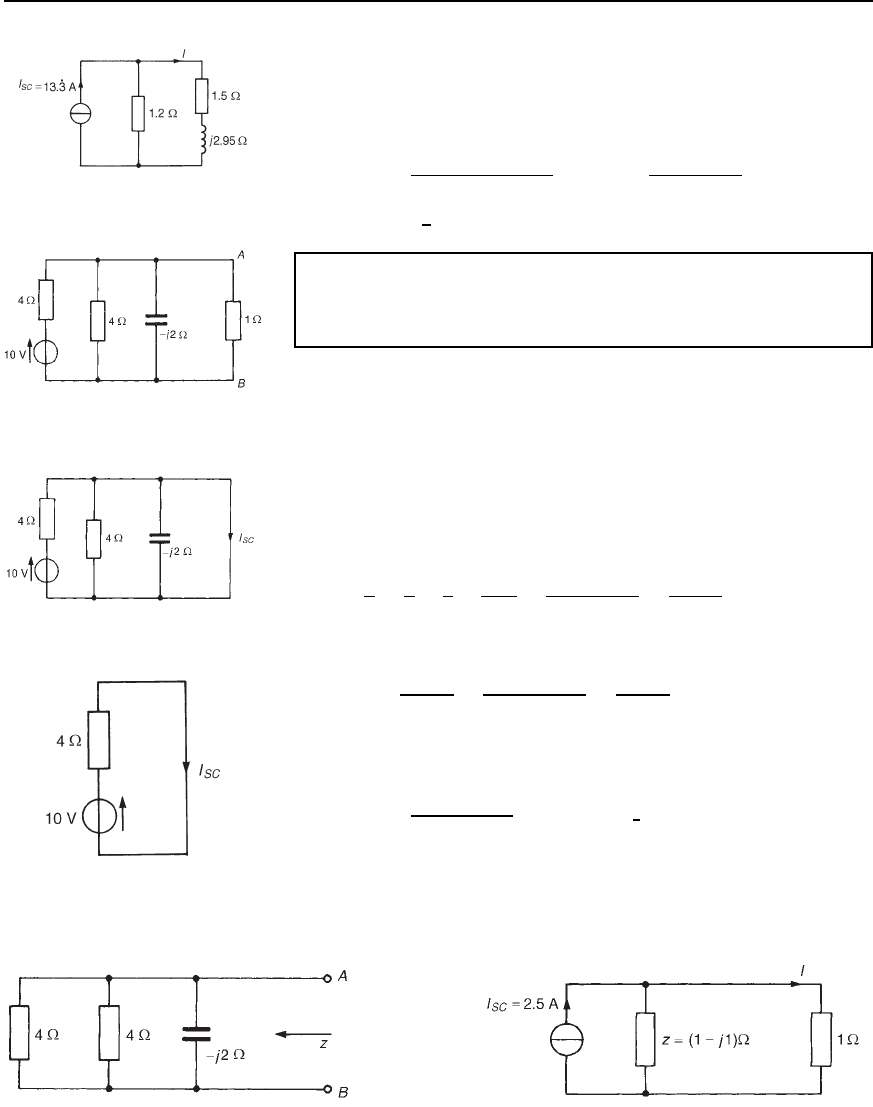
Problem 11. Use Norton’s theorem to determine the magnitude
of the p.d. across the 1 resistance of the network shown in
Figure 33.55.
Figure 33.55
(i) The branch containing the 1 resistance is initially short-circuited,
as shown in Figure 33.56.
Figure 33.56
(ii) 4 in parallel with j2 in parallel with 0 (i.e., the
short-circuit) is equivalent to 0, giving the equivalent circuit of
Figure 33.57. Hence I
SC
D 10/4 D 2.5A.
Figure 33.57
(iii) The 10 V source is removed from the network of Figure 33.55, as
shown in Figure 33.58, and the impedance z, ‘looking in’ at a break
made in AB is given by
1
z
D
1
4
C
1
4
C
1
j2
D
j j C 2
j4
D
2 j2
j4
from which
z D
j4
2 j2
D
j42 C j2
2
2
C 2
2
D
8 j8
8
D .1
− j1/Z
(iv) The Norton equivalent network is shown in Figure 33.59, from
which current I is given by
I D
1 j1
1 j1 C 1
2.5 D 1.58
6
18.43
°
A
Hence the magnitude of the p.d. across the 1 Z resistor is
given by
IR D 1.581 D 1.58 V.
Figure 33.58 Figure 33.59
Th´evenin’s and Norton’s theorems 591
Figure 33.60 Figure 33.61
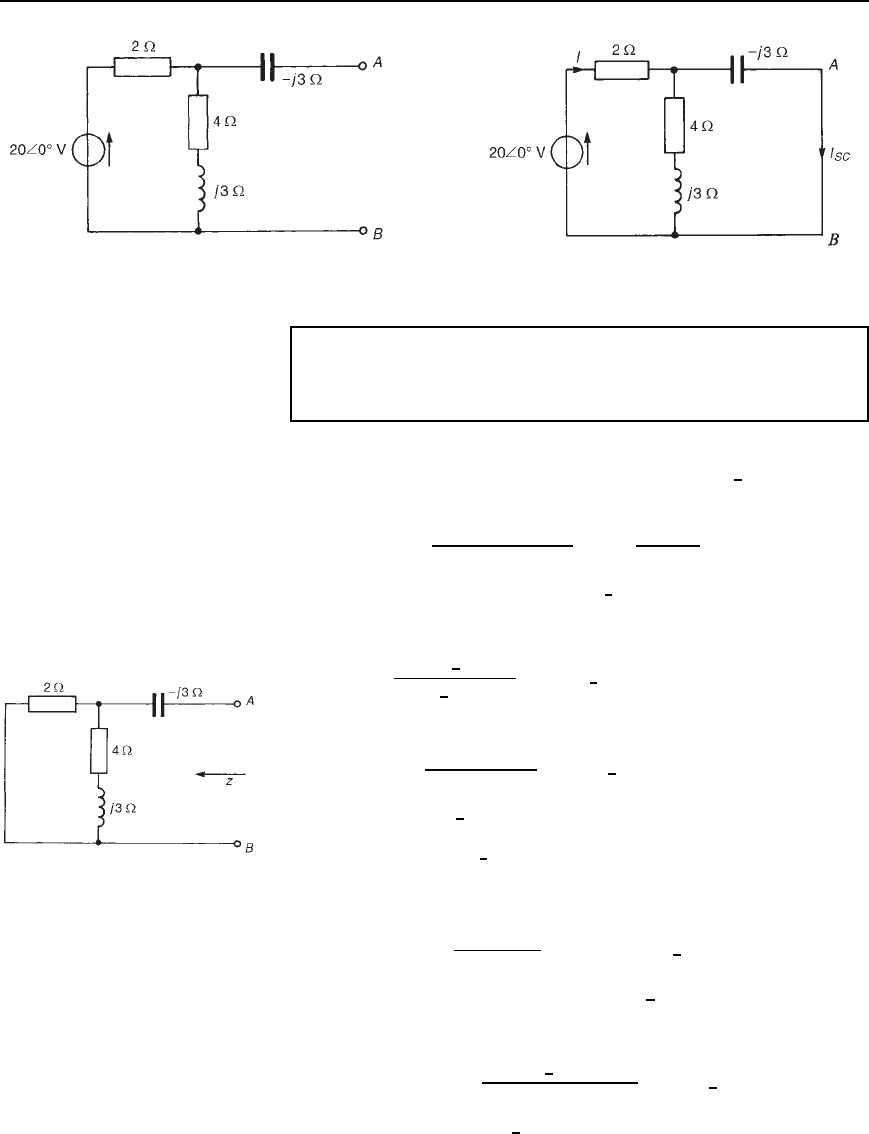
Problem 12. For the network shown in Figure 33.60, obtain the
Norton equivalent network at terminals AB. Hence determine the
power dissipated in a 5 resistor connected between A and B.
(i) Terminals AB are initially short-circuited, as shown in Figure 33.61.
(ii) The circuit impedance Z presented to the 20
6
0
°
V source is
given by
Z D 2 C
4 C j3j3
4 C j3 C j3
D 2 C
9 j12
4
D 4.25 j3 or 5.202
6
35.22
°
Thus current I in Figure 33.61 is given by
I D
20
6
0
°
5.202
6
35.22
°
D 3.845
6
35.22
°
A
Hence
I
SC
D
4 C j3
4 C j3 j3
3.845
6
35.22
°
D 4.806
66
72.09
°
A
(iii) Removing the 20
6
0
°
V source of Figure 33.60 gives the network
of Figure 33.62.
Figure 33.62
Impedance, z, ‘looking in’ at terminals AB is given by
z Dj3 C
24 C j3
2 C 4 C j3
Dj3 C 1.491
6
10.3
°
D .1.467 − j2.733/Z or 3.102
66
−61.77
°
Z
(iv) The Norton equivalent network is shown in Figure 33.63.
Current I
L
D
3.102
6
61.77
°
1.467 j2.733 C 5
4.806
6
72.09
°
D 2.123
6
33.23
°
A
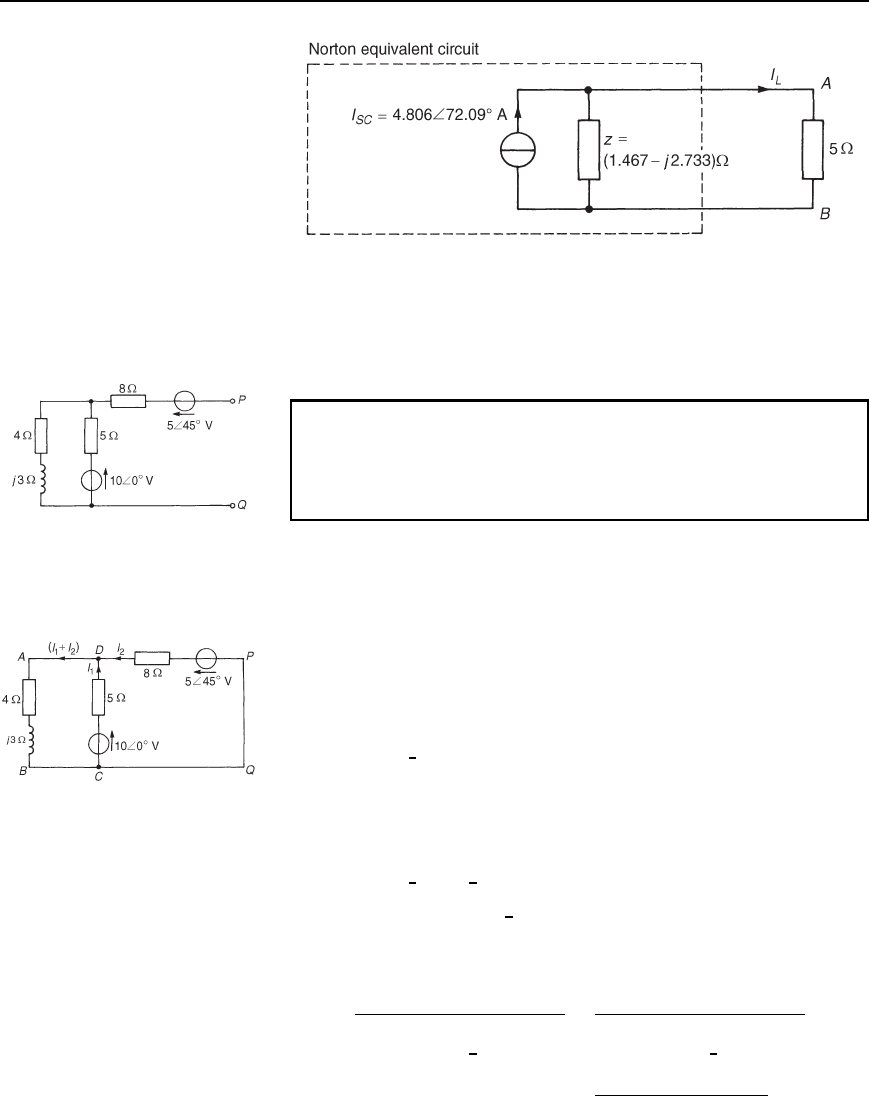
592 Electrical Circuit Theory and Technology
Figure 33.63
Hence the power dissipated in the 5 Z resistor is
I
2
L
R D 2.123
2
5 D 22.5W
Problem 13. Derive the Norton equivalent network with respect
to terminals PQ for the network shown in Figure 33.64 and hence
determine the magnitude of the current flowing in a 2 resistor
connected across PQ.
Figure 33.64
This is the same problem as problem 7 on page 584 which was solved
by Th
´
evenin’s theorem.
A comparison of methods may thus be made.
(i) Terminals PQ are initially short-circuited, as shown in Figure 33.65.
(ii) Currents I
1
and I
2
are shown labelled. Kirchhoff’s laws are used.
For loop ABCD, and moving anticlockwise,
10
6
0
°
D 5I
1
C 4 Cj3I
1
C I
2
,
i.e., 9 C j3I
1
C 4 Cj3I
2
10 D 0 1
Figure 33.65
For loop DPQC, and moving clockwise,
10
6
0
°
5
6
45
°
D 5I
1
8I
2
,
i.e., 5I
1
8I
2
C 5
6
45
°
10 D 0 2
Solving Equations (1) and (2) by using determinants gives
I
1
4 C j3 10
8 5
6
45
°
10
D
I
2
9 C j3 10
5 5
6
45
°
10
D
I
9 C j34 C j3
5 8
Th´evenin’s and Norton’s theorems 593
from which
I
2
D
9 C j3 10
5 5
6
45
°
10
9 C j34 C j3
5 8
D
[9 C j35
6
45
°
10 C 50]
[72 j24 20 j15]
D
[22.52
6
146.50
°
]
[99.925
6
157.03
°
]
D0.225
6
303.53
°
or 0.225
6
56.47
°
Hence the short-circuit current I
SC
D 0.225
6
56.47
°
A flowing
from P to Q.
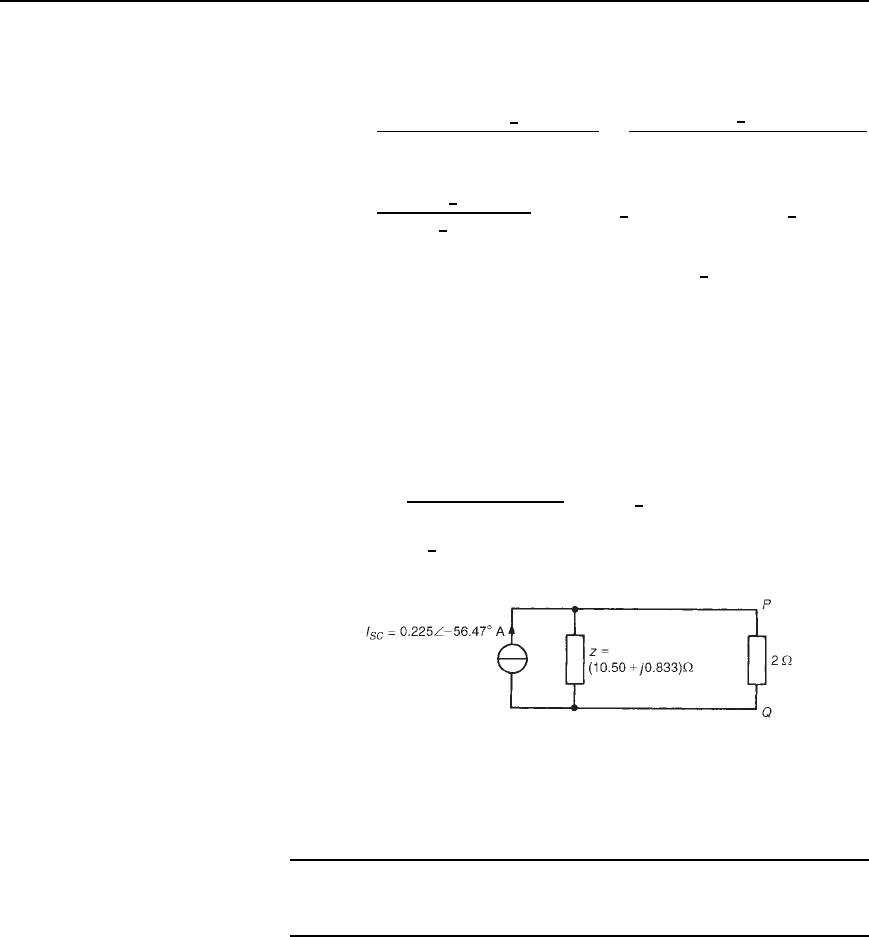
(iii) The impedance, z, ‘looking in’ at a break made between P and Q
is given by
z D 10.50 C j0.833 (see problem 7, page 584).
(iv) The Norton equivalent circuit is shown in Figure 33.66, where
current I is given by
I D
10.50 C j0.833
10.50 Cj0.833 C 2
0.225
6
56.47
°
D 0.19
6
55.74
°
A
Figure 33.66
Hence the magnitude of the current flowing in the 2 Z resistor
is 0.19 A.
Further problems on Norton’s theorem may be found in Section 33.5,
problems 11 to 15, page 600
33.4 Th
´
evenin and
Norton equivalent
networks
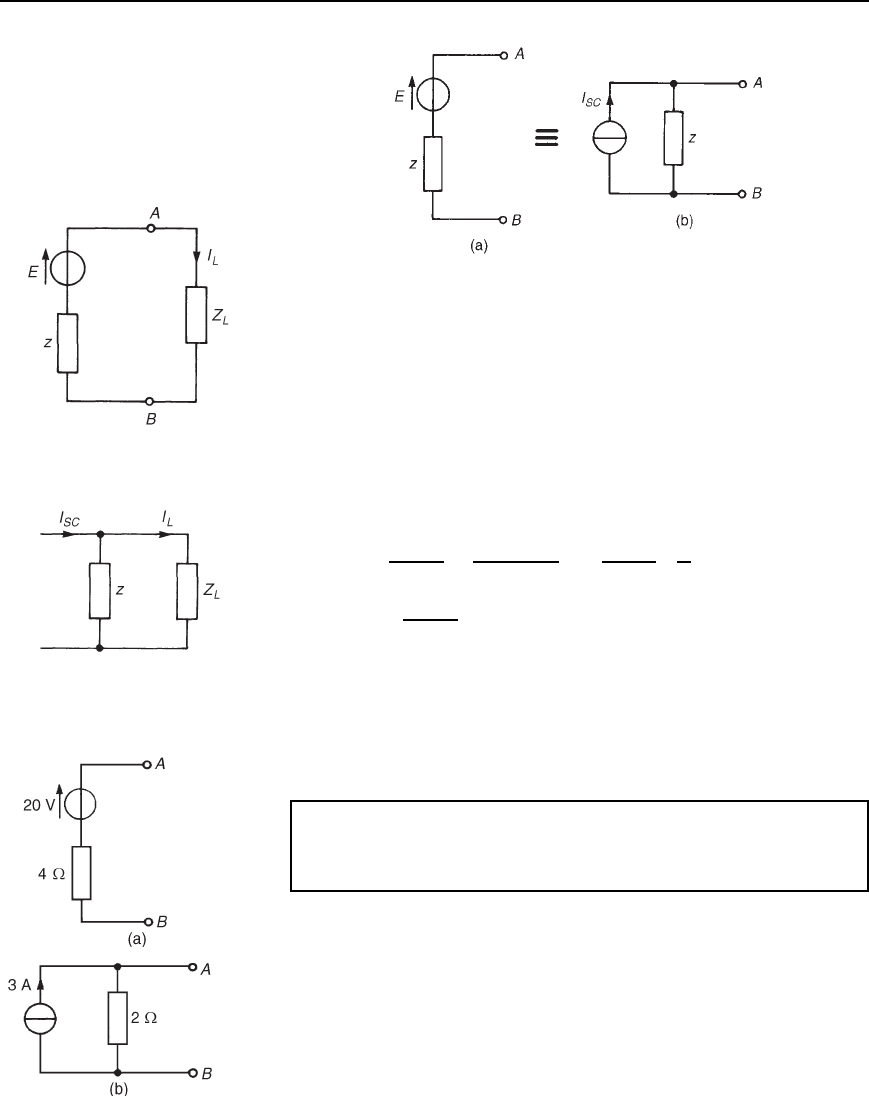
It is seen in Sections 33.2 and 33.3 that when Th
´
evenin’s and Norton’s
theorems are applied to the same circuit, identical results are obtained.
Thus the Th
´
evenin and Norton networks shown in Figure 33.67 are equiv-
alent to each other. The impedance ‘looking in’ at terminals AB is the
same in each of the networks; i.e., z.
If terminals AB in Figure 33.67(a) are short-circuited, the short-circuit
current is given by E/z.
594 Electrical Circuit Theory and Technology
Figure 33.67 Equivalent Th´evenin and Norton circuits
If terminals AB in Figure 33.67(b) are short-circuited, the short-circuit
current is I
SC
.
Thus I
SC
D E=z.
Figure 33.68
Figure 33.68 shows a source of e.m.f. E in series with an impedance z
feeding a load impedance Z
L
. From Figure 33.68,
I
L
D
E
z C Z
L
D
E/z
z C Z
L
/z
D
z
z C Z
L
E
z
i.e., I
L
D
z
z Y Z
L
I
SC
, from above.
From Figure 33.69 it can be seen that, when viewed from the load, the
source appears as a source of current I
SC
which is divided between z and
Z
L
connected in parallel.
Figure 33.69
Thus it is shown that the two representations shown in Figure 33.67 are
equivalent.
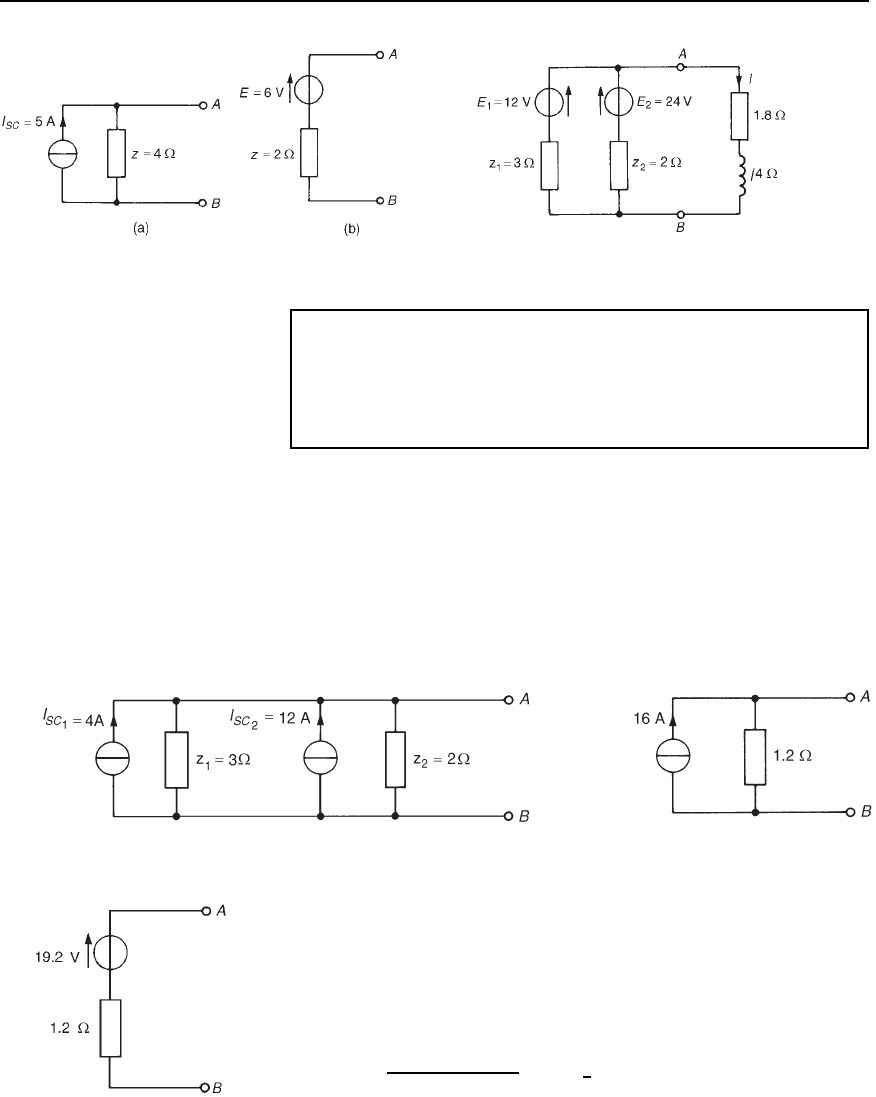
Problem 14. (a) Convert the circuit shown in Figure 33.70(a) to
an equivalent Norton network. (b) Convert the network shown in
Figure 33.70(b) to an equivalent Th
´
evenin circuit.
(a) If the terminals AB of Figure 33.70(a) are short circuited, the short-
circuit current, I
SC
D 20/4 D 5 A. The impedance ‘looking in’ at
terminals AB is 4 . Hence the equivalent Norton network is as
shown in Figure 33.71(a).
(b) The open-circuit voltage E across terminals AB in Figure 33.70(b)
is given by E D I
SC
z D 32 D 6 V. The impedance ‘looking
in’ at terminals AB is 2 .
Hence the equivalent Th
´
evenin circuit is as shown in
Figure 33.71(b).
Figure 33.70
Th´evenin’s and Norton’s theorems 595
Figure 33.71 Figure 33.72
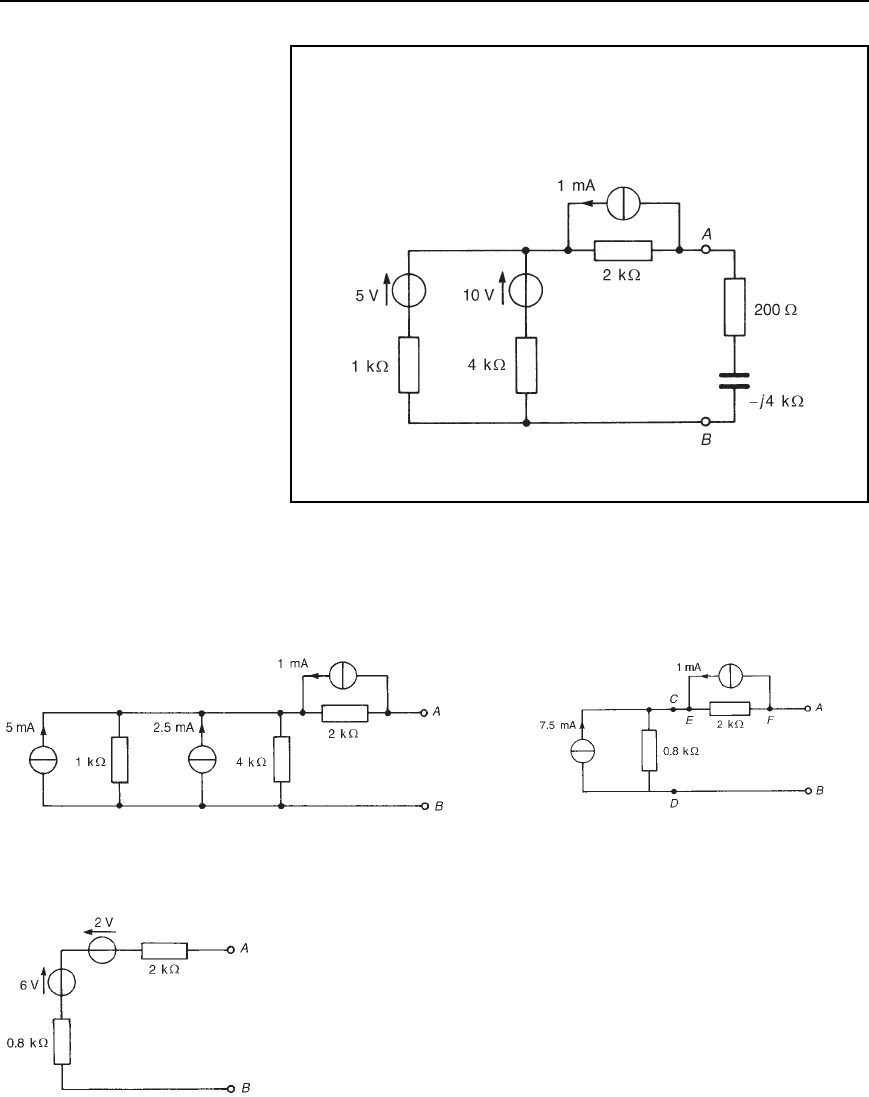
Problem 15. (a) Convert the circuit to the left of terminals AB
in Figure 33.72 to an equivalent Th
´
evenin circuit by initially
converting to a Norton equivalent circuit. (b) Determine the
magnitude of the current flowing in the 1.8 C j4 impedance
connected between terminals A and B of Figure 33.72.
(a) For the branch containing the 12 V source, conversion to a Norton
equivalent network gives I
SC
1
D 12/3 D 4A and z
1
D 3 . For
the branch containing the 24 V source, conversion to a Norton
equivalent circuit gives I
SC
2
D 24/2 D 12Aandz
2
D 2 .
Thus Figure 33.73 shows a network equivalent to Figure 33.72.
From Figure 33.73, the total short-circuit current is 4 C 12 D 16 A,
and the total impedance is given by 3 ð 2/3 C2 D 1.2 . Thus
Figure 33.73 simplifies to Figure 33.74.
Figure 33.73 Figure 33.74
The open-circuit voltage across AB of Figure 33.74, E D
161.2 D 19.2 V, and the impedance ‘looking in’ at AB, z D
1.2 . Hence the Th
´
evenin equivalent circuit is as shown in
Figure 33.75.
(b) When the 1.8 C j4 impedance is connected to terminals AB of
Figure 33.75, the current I flowing is given by
I D
19.2
1.2 C 1.8 Cj4
D 3.84
6
53.13
°
A
Hence the current flowing in the .1.8Yj4/Z impedance is 3.84 A.
Figure 33.75
596 Electrical Circuit Theory and Technology
Problem 16. Determine, by successive conversions between
Th
´
evenin’s and Norton’s equivalent networks, a Th
´
evenin
equivalent circuit for terminals AB of Figure 33.76. Hence
determine the magnitude of the current flowing in the capacitive
branch connected to terminals AB.
Figure 33.76
For the branch containing the 5 V source, converting to a Norton
equivalent network gives I
SC
D 5/1000 D 5mAandz D 1k. For the
branch containing the 10 V source, converting to a Norton equivalent
network gives I
SC
D 10/4000 D 2.5mAandz D 4k. Thus the circuit
of Figure 33.76 converts to that of Figure 33.77.
Figure 33.77 Figure 33.78
The above two Norton equivalent networks shown in Figure 33.77 may
be combined, since the total short-circuit current is 5 C2.5 D 7.5mA
and the total impedance z is given by 1 ð 4/1 C 4 D 0.8k. This
results in the network of Figure 33.78.
Both of the Norton equivalent networks shown in Figure 33.78 may
be converted to Th
´
evenin equivalent circuits. Open-circuit voltage across
CD is
7.5 ð 10
3
0.8 ð 10
3
D 6V
and the impedance ‘looking in’ at CD is 0.8 k. Open-circuit voltage
across EF is 1 ð10
3
2 ð 10
2
D 2 V and the impedance ‘looking in’
at EF is 2 k. Thus Figure 33.78 converts to Figure 33.79.
Figure 33.79
Th´evenin’s and Norton’s theorems 597
Figure 33.80
Combining the two Th
´
evenin circuits gives e.m.f. E D 6 2 D 4V,
and impedance z D 0.8 C 2 D 2.8kZ. Thus the Th
´
evenin equivalent
circuit for terminals AB of Figure 33.76 is as shown in Figure 33.80.
If an impedance 200 j4000 is connected across terminals AB,
then the current I flowing is given by
I D
4
2800 C 200 j4000
D
4
5000
6
53.13
°
D 0.80
6
53.13
°
mA
i.e., the current in the capacitive branch is 0.80 mA.
Problem 17. (a) Determine an equivalent Th
´
evenin circuit for
terminals AB of the network shown in Figure 33.81. (b) Calculate
the power dissipated in a 600 j800 impedance connected
between A and B of Figure 33.81.
Figure 33.81
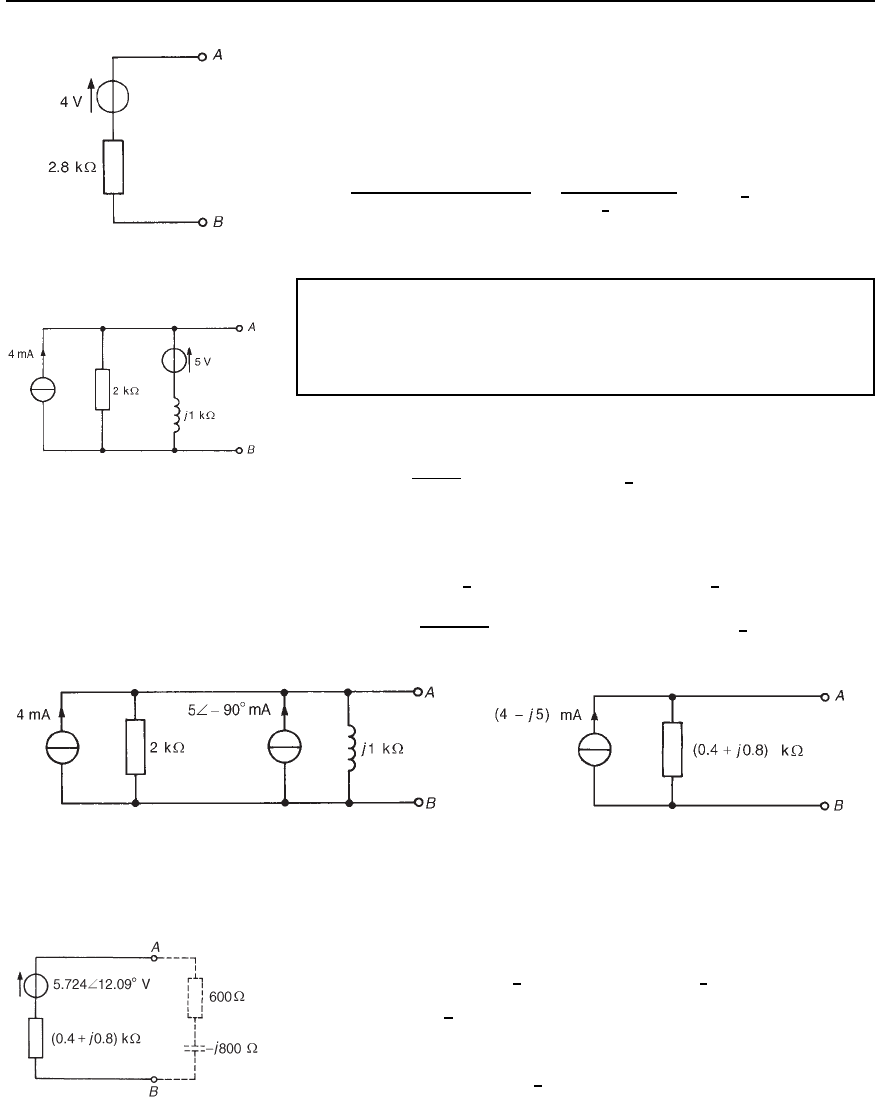
(a) Converting the Th
´
evenin circuit to a Norton network gives
I
SC
D
5
j1000
Dj5mA or 5
6
90
°
mA and z D j1k
Thus Figure 33.81 converts to that shown in Figure 33.82. The two
Norton equivalent networks may be combined, giving
I
SC
D 4 C 5
6
90
°
D 4 j5mA or 6.403
6
51.34
°
mA
and z D
2j1
2 C j1
D 0.4 C j0.8k or 0.894
6
63.43
°
k
Figure 33.82 Figure 33.83
This results in the equivalent network shown in Figure 33.83.
Converting to an equivalent Th
´
evenin circuit gives open circuit
e.m.f. across AB,
E D 6.403 ð 10
3
6
51.34
°
0.894 ð 10
3
6
63.43
°
D 5.724
66
12.09
°
V
and
impedance z D 0.894
6
63.43
°
k or .400 Y j800/Z
Thus the Th
´
evenin equivalent circuit is as shown in Figure 33.84.
Figure 33.84
