Bird J. Electrical Circuit Theory and Technology
Подождите немного. Документ загружается.

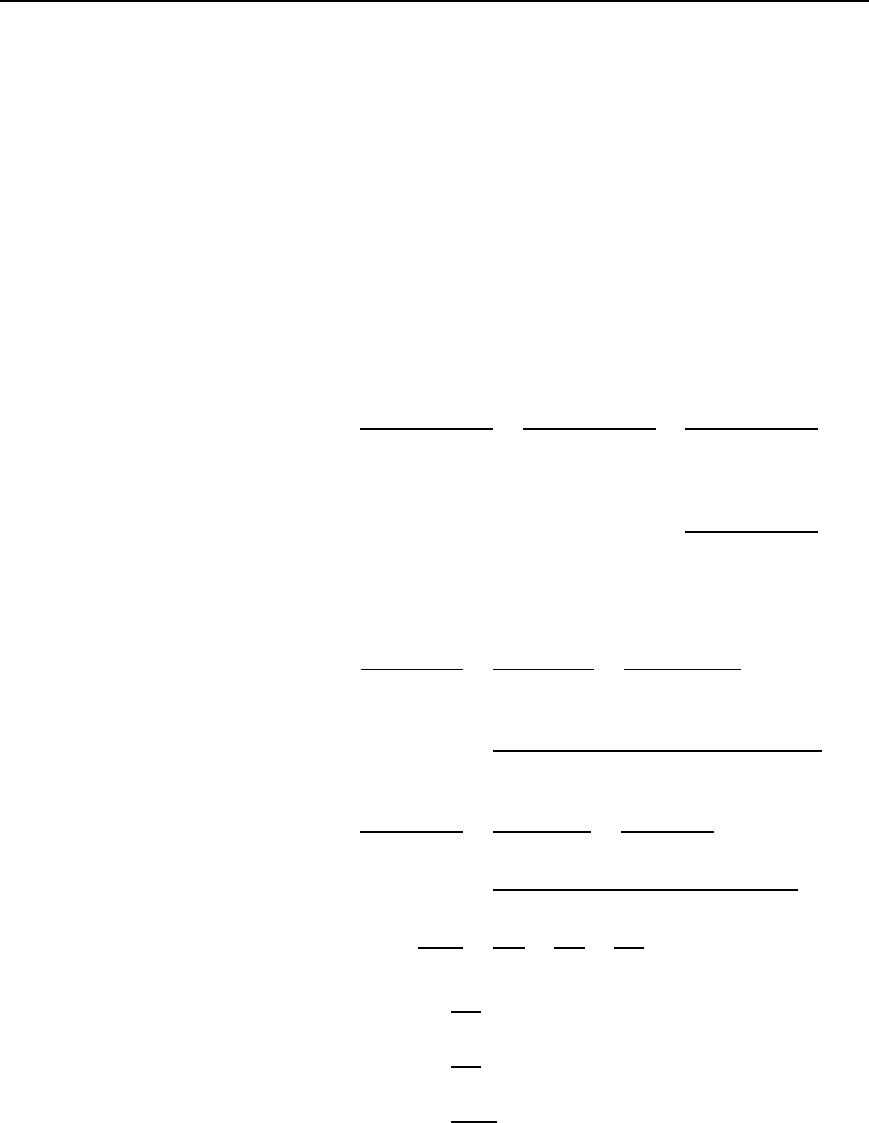
538 Electrical Circuit Theory and Technology
From loop EDGF, and moving clockwise,
6I
2
C 2I
3
1I
1
I
2
D 0
i.e., I
1
C 7I
2
C 2I
3
D 0 2
From loop DCHG, and moving anticlockwise,
2I
3
C 3I
1
I
2
C I
3
4I
2
I
3
D 0
i.e., 3I
1
7I
2
C 9I
3
D 0 3
(iii) Thus 5I
1
C 10I
2
4I
3
8 D 0
I
1
C 7I
2
C 2I
3
C 0 D 0
3I
1
7I
2
C 9I
3
C 0 D 0
Hence, using determinants,
I
1
10 4 8
720
79 0
D
I
2
5 4 8
12 0
390
D
I
3
5108
17 0
3 70
D
1
5104
17 2
3 79
Thus
I
1
8
72
79
D
I
2
8
12
39
D
I
3
8
17
3 7
D
1
5
72
79
10
12
39
4
17
3 7
I
1
863 C 14
D
I
2
89 6
D
I
3
87 21
D
1
563 C 14 109 6 47 21
I
1
616
D
I
2
120
D
I
3
112
D
1
591
Hence I
1
D
616
591
D 1.042 A,
I
2
D
120
591
D 0.203 A and
I
3
D
112
591
D0.190 A

Introduction to network analysis 539
Thus the current flowing in the 2 Z resistance is 0.190 A in the opposite
direction to that shown in Figure 30.6.
Current in the 3 resistance D I
1
I
2
C I
3
D 1.042 0.203 C 0.190 D 0.649 A.
Hence power dissipated in the 3 Z resistance, I
2
3 D 0.649
2
3 D
1.26W
Problem 3. For the a.c. network shown in Figure 30.7, determine
the current flowing in each branch using Kirchhoff’s laws.
Figure 30.7
(i) Currents I
1
and I
2
with their directions are shown in Figure 30.8.
Figure 30.8
(ii) Two loops are chosen with their directions both clockwise.
From loop ABEF, 5 C j0 D I
1
3 C j4 C I
1
I
2
6 C j8
i.e., 5 D 9 C j12I
1
6 Cj8I
2
1
From loop BCDE, 2 C j4 D I
2
2 j5 I
1
I
2
6 C j8
i.e., 2 C j4 D6 C j8I
1
C 8 Cj3I
2
2
(iii) Multiplying equation (1) by 8 C j3 gives:
58 C j3 D 8 C j39 C j12I
1
8 Cj36 C j8I
2
3
Multiplying equation (2) by 6 C j8 gives:
6 C j82 C j4 D6 C j86 Cj8I
1
C 6 Cj88 C j3I
2
4
Adding equations (3) and (4) gives:
58 C j3 C 6 C j82 C j4 D [8 C j39 Cj12
6 C j86 C j8]I
1
i.e., 20 C j55 D 64 C j27I
1

540 Electrical Circuit Theory and Technology
from which, I
1
D
20 C j55
64 C j27
D
58.52
6
70.02
°
69.46
6
22.87
°
D 0.842
66
47.15
°
A
D 0.573 C j0.617 A
D .0.57 Y j0.62/ A, correct to two decimal places.
From equation (1), 5 D 9 C j120.573 C j0.617 6 C j8I
2
5 D 2.247 C j12.429 6 C j8I
2
from which, I
2
D
2.247 Cj12.429 5
6 C j8
D
14.39
6
120.25
°
10
6
53.13
°
D 1.439
66
67.12
°
A D 0.559 C j1.326 A
D .0.56 Y j1.33/A, correct to two decimal places.
The current in the 6 C j8 impedance,
I
1
I
2
D 0.573 C j0.617 0.559 C j1.326
D .0.014
− j0.709/A or 0.709
66
−88.87
°
A
An alternative method of solving equations (1) and (2) is shown below,
using determinants.
9 C j12I
1
6 C j8I
2
5 D 0 1
6 C j8I
1
C 8 Cj3I
2
2 Cj4 D 0 2
Thus
I
1
6 C j8 5
8 C j3 2 Cj4
D
I
2
9 C j12 5
6 C j8 2 C j4
D
1
9 C j12 6 C j8
6 C j88 C j3
I
1
20 C j40 C 40 C j15
D
I
2
30 j60 30 C j40
D
1
36 C j123 28 C j96
I
1
20 C j55
D
I
2
j100
D
1
64 C j27
Hence I
1
D
20 C j55
64 C j27
D
58.52
6
70.02
°
69.46
6
22.87
°
D 0.842
66
47.15
°
A
Introduction to network analysis 541
and I
2
D
100
6
90
°
69.46
6
22.87
°
D 1.440
66
67.13
°
A
The current flowing in the 6 Cj8impedance is given by:
I
1
I
2
D 0.842
6
47.15
°
1.440
6
67.13
°
A
D .0.013
− j0.709/ A or 0.709
66
−88.95
°
A
Problem 4. For the network shown in Figure 30.9, use Kirch-
hoff’s laws to determine the magnitude of the current in the
4 C j3impedance.
(i) Currents I
1
, I
2
and I
3
with their directions are shown in
Figure 30.10. The current in the 4 C j3impedance is specified
by one symbol only (i.e., I
3
), which means that the three equations
formed need to be solved for only one unknown current.
Figure 30.9 Figure 30.10
(ii) Three loops are chosen. From loop ABGH, and moving clockwise,
4I
1
j5I
2
D 10 C 12 1
From loop BCFG, and moving anticlockwise,
j5I
2
8I
1
I
2
I
3
D 15 C 12 2
From loop CDEF, and moving clockwise,
8I
1
I
2
I
3
C 4 C j3I
3
D 15 3
Hence
4I
1
j5I
2
C 0I
3
22 D 0
8I
1
C 8 j5I
2
C 8I
3
27 D 0
8I
1
C 8I
2
C 12 Cj3I
3
15 D 0

542 Electrical Circuit Theory and Technology
Solving for I
3
using determinants gives:
I
3
4 j5 22
8 8 j5 27
8815
D
1
4 j50
8 8 j5 8
8812 C j3
Thus
I
3
4
8 j5 27
8 15
C j5
8 27
8 15
22
8 8 j5
88
D
1
4
8 j5 8
8 12 Cj3
C j5
88
8 12 C j3
Hence
I
3
384 C j700
D
1
308 j304
from which,
I
3
D
384 C j700
308 j304
D
798.41
6
118.75
432.76
6
44.63
°
D 1.85
6
74.12
°
A
Hence the magnitude of the current flowing in the .4 Y j3/Z
impedance is 1.85 A
Further problems on network analysis using Kirchhoff’s laws may be found
in Section 30.4 following, problems 1 to 10.
30.4 Further problems
on Kirchhoff’s laws
1 For the network shown in Figure 30.11, determine the current
flowing in each branch.
[50 V source discharges at 2.08 A,
20 V source charges at 0.62 A,
current through 20 resistor is 1.46 A]
2. Determine the value of currents I
A
, I
B
and I
C
for the network shown
in Figure 30.12. [I
A
D 5.38 A, I
B
D 4.81 A, I
C
D 0.58 A]
3. For the bridge shown in Figure 30.13, determine the current flowing
in (a) the 5 resistance, (b) the 22 resistance, and (c) the 2
resistance. [(a) 4 A (b
)1A(c)7A]
4. For the circuit shown in Figure 30.14, determine (a) the current
flowing in the 10 V source, (b) the p.d. across the 6 resistance,
and (c) the active power dissipated in the 4 resistance.
[(a) 1.59 A (b) 3.71 V (c) 3.79 W]
Figure 30.11
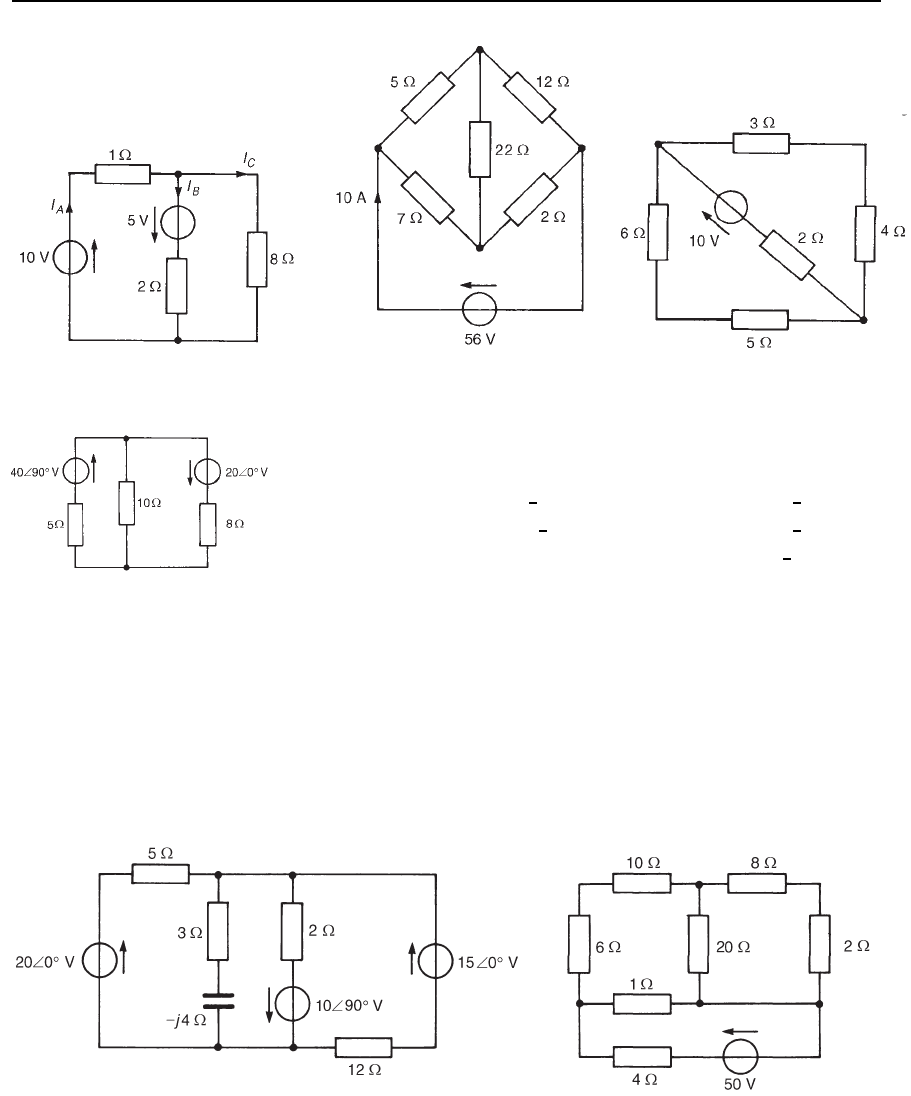
Introduction to network analysis 543
Figure 30.12 Figure 30.13 Figure 30.14
5. Use Kirchhoff’s laws to determine the current flowing in each branch
of the network shown in Figure 30.15.
[40
6
90
°
V source discharges at 4.40
6
74.48
°
A
20
6
0
°
V source discharges at 2.94
6
53.13
°
A
current in 10 resistance is 1.97
6
107.35
°
A
(downward)]
Figure 30.15
6. For the network shown in Figure 30.16, use Kirchhoff’s laws to
determine the current flowing in the capacitive branch. [1.58 A]
7. Use Kirchhoff’s laws to determine, for the network shown in
Figure 30.17, the current flowing in (a) the 20 resistance, and
(b) the 4 resistance. Determine also (c) the p.d. across the 8
resistance, and (d) the active power dissipated in the 10 resistance.
[(a) 0.14 A (b) 10.1 A (c) 2.27 V (d) 1.81 W]
Figure 30.16 Figure 30.17

544 Electrical Circuit Theory and Technology
Figure 30.18 Figure 30.19
8. Determine the value of currents I
A
, I
B
and I
C
shown in the network
of Figure 30.18, using Kirchhoff’s laws.
[I
A
D 2.80
6
59.59
°
A, I
B
D 2.71
6
58.78
°
A,
I
C
D 0.097
6
97.13
°
A]
9. Use Kirchhoff’s laws to determine the currents flowing in (a) the
3 resistance, (b) the 6 resistance and (c) th
e 4 V source of the
network shown in Figure 30.19. Determine also the active power
dissipated in the 5 resistance.
[(a) 0.27 A (b) 0.70 A (c) 0.29 A discharging (d) 1.60 W]
10. Determine the magnitude of the p.d. across the 8 Cj6impe-
dance shown in Figure 30.20 by using Kirchhoff’s laws. [11.37 V]
Figure 30.20
31 Mesh-current and
nodal analysis
At the end of this chapter you should be able to:
ž solve d.c. and a.c. networks using mesh-current analysis
ž solve d.c. and a.c. networks using nodal analysis
31.1 Mesh-current
analysis
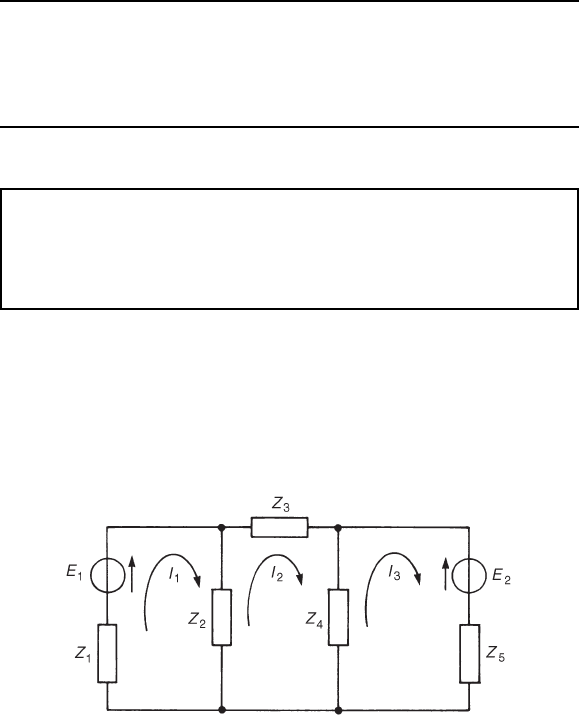
Mesh-current analysis is merely an extension of the use of Kirchhoff’s
laws, explained in Chapter 30. Figure 31.1 shows a network whose circu-
lating currents I
1
, I
2
and I
3
have been assigned to closed loops in the
circuit rather than to branches. Currents I
1
,I
2
and I
3
are called mesh-
currents or loop-currents.
Figure 31.1
In mesh-current analysis the loop-currents are all arranged to circu-
late in the same direction (in Figure 31.1, shown as clockwise direction).
Kirchhoff’s second law is applied to each of the loops in turn, which
in the circuit of Figure 31.1 produces three equations in three unknowns
which may be solved for I
1
,I
2
and I
3
. The three equations produced from
Figure 31.1 are:
I
1
Z
1
C Z
2
I
2
Z
2
D E
1
I
2
Z
2
C Z
3
C Z
4
I
1
Z
2
I
3
Z
4
D 0
I
3
Z
4
C Z
5
I
2
Z
4
DE
2
The branch currents are determined by taking the phasor sum of the
mesh currents common to that branch. For example, the current flowing

546 Electrical Circuit Theory and Technology
in impedance Z
2
of Figure 31.1 is given by (I
1
I
2
) phasorially. The
method of mesh-current analysis, called Maxwell’s theorem, is demon-
strated in the following problems.
Problem 1. Use mesh-current analysis to determine the current
flowing in (a) the 5 resistance, and (b) the 1 resistance of the
d.c. circuit shown in Figure 31.2.
Figure 31.2
The mesh currents I
1
, I
2
and I
3
are shown in Figure 31.2. Using Kirch-
hoff’s voltage law:
For loop 1,3 C 5I
1
5I
2
D 4 1
For loop 2,4 C 1 C6 C 5I
2
5I
1
1I
3
D 0 2
For loop 3,1 C 8I
3
1I
2
D5 3
Thus
8I
1
5I
2
4 D 0 1
0
5I
1
C 16I
2
I
3
D 0 2
0
I
2
C 9I
3
C 5 D 0 3
0
Using determinants,
I
1
504
16 10
19 5
D
I
2
804
5 10
095
D
I
3
8 5 4
516 0
0 15
D
1
8 50
5161
0 19

Mesh-current and nodal analysis 547
I
1
5
10
95
4
16 1
19
D
I
2
8
10
95
4
5 1
09
D
I
3
4
516
0 1
C 5
8 5
516
D
1
8
16 1
19
C 5
5 1
09
I
1
55 4143
D
I
2
85 445
D
I
3
45 C 5103
D
1
8143 C 545
I
1
547
D
I
2
140
D
I
3
495
D
1
919
Hence I
1
D
547
919
D 0.595 A, I
2
D
140
919
D 0.152 A, and
I
3
D
495
919
D0.539 A
Thus current in the 5 Z resistance D I
1
I
2
D 0.595 0.152
D 0.44 A,
and current in the 1 Z resistance D I
2
I
3
D 0.152 0.539
D 0.69 A
Problem 2. For the a.c. network shown in Figure 31.3 determine,
using mesh-current analysis, (a) the mesh currents I
1
and I
2
(b) the
current flowing in the capacitor, and (c) the active power delivered
by the 100
6
0
°
V voltage source.
Figure 31.3
(a) For the first loop 5 j4I
1
j4I
2
D 100
6
0
°
(1)
For the second loop 4 C j3 j4I
2
j4I
1
D 0(2)
Rewriting equations (1) and (2) gives:
5 j4I
1
C j4I
2
100 D 0 1
0
j4I
1
C 4 jI
2
C 0 D 0 2
0
