Bird J. Electrical Circuit Theory and Technology

Подождите немного. Документ загружается.

458 Electrical Circuit Theory and Technology

Figure 25.19 Figure 25.20

Figure 25.21 Figure 25.22

19 For the network shown in Figure 25.21, determine (a) the value of

impedance Z

, (b) the current ﬂowing in Z

, and (c) the components

comprising Z

if the supply frequency is 2 kHz

[(a) 6.25

52.34

 (b) 16.0

7.66

20 Coils of impedance 5 C j8 and 12 Cj16 are connected

in parallel. In series with this combination is an impedance of

15  j40. If the alternating supply pd. is 150

V, determine

(a) the equivalent network impedance, (b) the supply current, (c) the

supply phase angle, (d) the current in the 5 C j8 impedance, and

(e) the current in the 12 Cj16 impedance.

[(a) 39.31

61.84

 (b) 3.816

61.84

leading (d) 2.595

60.28

(e) 1.224

65.15

21 For circuit shown in Figure 25.22, determine (a) the input

impedance, (b) the source voltage V, (c) the p.d. between points A

and B, and (d) the current in the 10  resistor.

[(a) 10.0

36.87

 (b) 150

66.87

51.92

V (d) 2.50

18.23

26 Power in a.c. circuits

At the end of this chapter you should be able to:

ž determine active, apparent and reactive power in a.c.

series/parallel networks

ž appreciate the need for power factor improvement

ž perform calculations involving power factor improvement

26.1 Introduction

Alternating currents and voltages change their polarity during each cycle.

It is not surprising therefore to ﬁnd that power also pulsates with time.

The product of voltage

v and current i at any instant of time is called

instantaneous power p, and is given by:

= vi

26.2 Determination of

power in a.c. circuits

(a) Purely resistive a.c. circuits

Let a voltage

v D V

sinωt be applied to a circuit comprising resistance

only. The resulting current is i D I

sinωt, and the corresponding instan-

taneous power, p, is given by:

p D

vi D V

sinωtI

sinωt

i.e., p D V

sin

ωt

From trigonometrical double angle formulae, cos2A D 1 2sin

A, from

which,

sin

A D

1  cos2A

Thus sin

ωt D

1  cos2ωt

Then power p D V



1  cos2ωt



, i.e., p =

.1 − cos2!t/.

The waveforms of

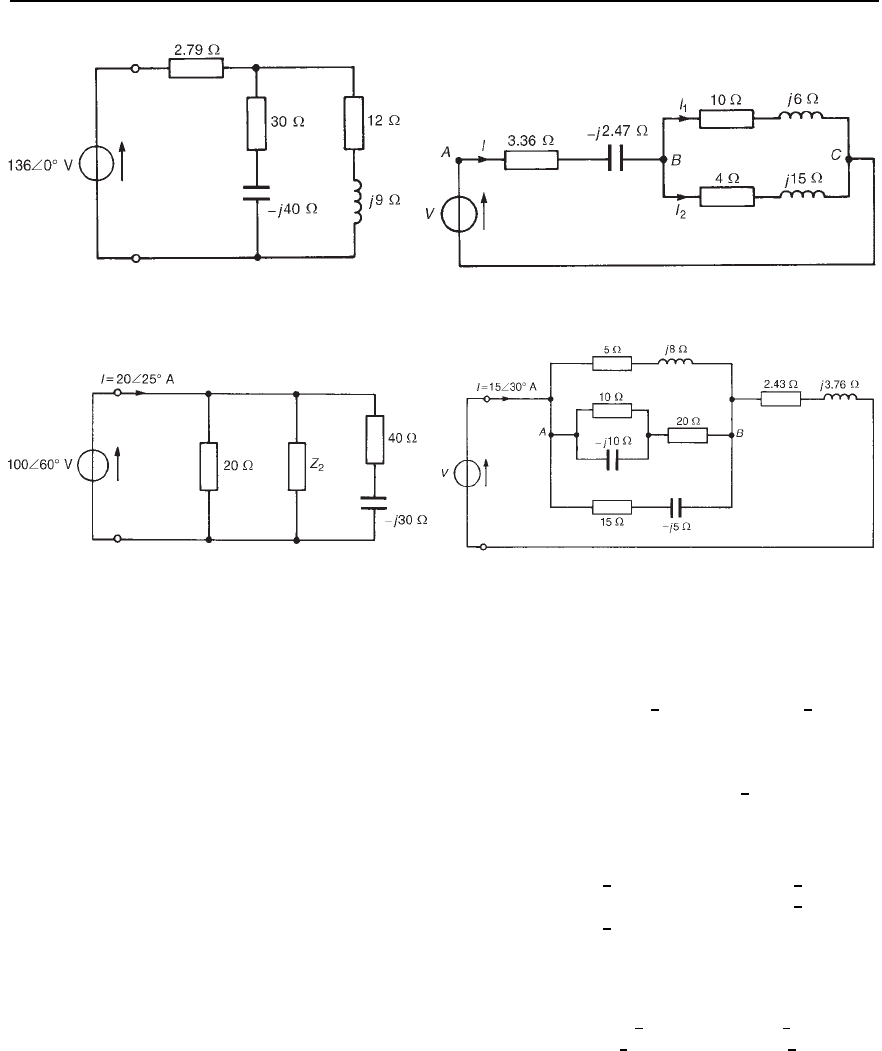
v, i and p are shown in Figure 26.1. The waveform

of power repeats itself after /ω seconds and hence the power has a

frequency twice that of voltage and current. The power is always positive,

having a maximum value of V

. The average or mean value of the

power is

The rms value of voltage V D 0.707 V

,i.e.V D V

2, from which,

2 V. Similarly, the rms value of current, I D I

2, from which,

2 I. Hence the average power, P, developed in a purely resistive

460 Electrical Circuit Theory and Technology

Figure 26.1 The waveforms of v, i and p

a.c. circuit is given by

P D



2 V

2 I D VI watts

Also, power P D I

R or V

/R as for a d.c. circuit, since V D IR.

Summarizing, the average power P in a purely resistive a.c. circuit is

given by

P = VI = I

R =

watts

where V and I are rms values.

(b) Purely inductive a.c. circuits

Let a voltage

v D V

sinωt be applied to a circuit containing pure induc-

tance (theoretical case). The resulting current is i D I

sinωt  /2

since current lags voltage by 90

in a purely inductive circuit, and the

corresponding instantaneous power, p, is given by:

p D

vi D V

sinωtI

sinωt  /2

i.e., p D V

sinωt sinωt  /2

However, sinωt  /2 Dcosωt

Thus p DV

sinωt cosωt

Rearranging gives: p D

2 sin ωt cosωt. However, from the

double-angle formulae, 2sinωt cosωt D sin 2ωt.

Thus power, p

= −

sin2!t

Power in a.c. circuits 461

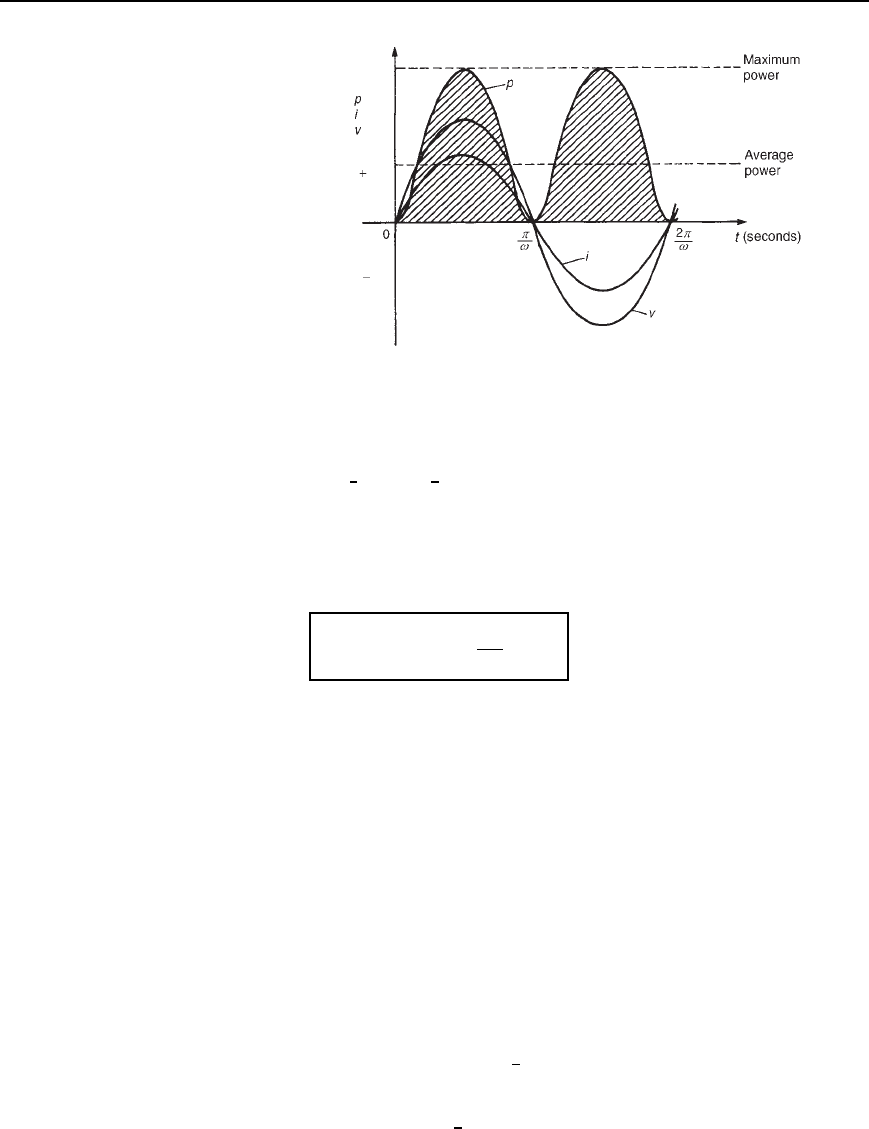
The waveforms of v, i and p are shown in Figure 26.2. The frequency of

power is twice that of voltage and current. For the power curve shown

in Figure 26.2, the area above the horizontal axis is equal to the area

below, thus over a complete cycle the average power P is zero. It is

noted that when

v and i are both positive, power p is positive and energy

is delivered from the source to the inductance; when

v and i have opposite

signs, power p is negative and energy is returned from the inductance to

the source.

Figure 26.2 Power in a purely inductive a.c. circuit

In general, when the current through an inductance is increasing, energy

is transferred from the circuit to the magnetic ﬁeld, but this energy is

returned when the current is decreasing.

Summarizing, the average power P in a purely inductive a.c. circuit

is zero.

Let a voltage

v D V

sinωt be applied to a circuit containing pure capac-

itance. The resulting current is i D I

sinωt C /2, since current leads

voltage by 90

in a purely capacitive circuit, and the corresponding instan-

taneous power, p, is given by:

p D

vi D V

sinωtI

sinωt C /2

i.e., p D V

sinωt sinωt C /2

However, sinωt C /2 D cosωt.

Thus P D V

sinωt cosωt

Rearranging gives p D

2 sin ωt cosωt.

Thus power, p

sin2!t

462 Electrical Circuit Theory and Technology

The waveforms of v, i and p are shown in Figure 26.3. Over a complete

cycle the average power P is zero. When the voltage across a capacitor

is increasing, energy is transferred from the circuit to the electric ﬁeld,

but this energy is returned when the voltage is decreasing.

Figure 26.3 Power in a purely capacitive a.c. circuit

Summarizing, the average power P in a purely capacitive a.c. circuit

is zero.

(d) R–L or R–C a.c. circuits

Let a voltage

v D V

sinωt be applied to a circuit containing resistance

and inductance or resistance and capacitance. Let the resulting current

be i D I

sinωt C , where phase angle  will be positive for an R–C

circuit and negative for an R –L circuit. The corresponding instantaneous

power, p, is given by:

p D

vi D V

sinωtI

sinωt C 

i.e., p D V

sinωt sinωt C 

Products of sine functions may be changed into differences of cosine

functions by using: sinA sinB D

[cosA C B  cosA  B]

Substituting ωt D A and ωt C  D B gives:

power, p D V



[cosωt C ωt C   cosωt  ωt C ]



i.e., p D

[cos  cos2ωt C ]

However, cos D cos.

Thus p

[cosf − cos.2!t Y f/]

Power in a.c. circuits 463

The instantaneous power p thus consists of

(i) a sinusoidal term, 

cos2ωt C , which has a mean value

over a cycle of zero, and

(ii) a constant term,

cos (since  is constant for a particular

circuit).

Thus the average value of power, P D

cos.

Since V

2 V and I

2 I,

average power, P D



2 V

2 I cos

i.e.,

P = VI cosf watts

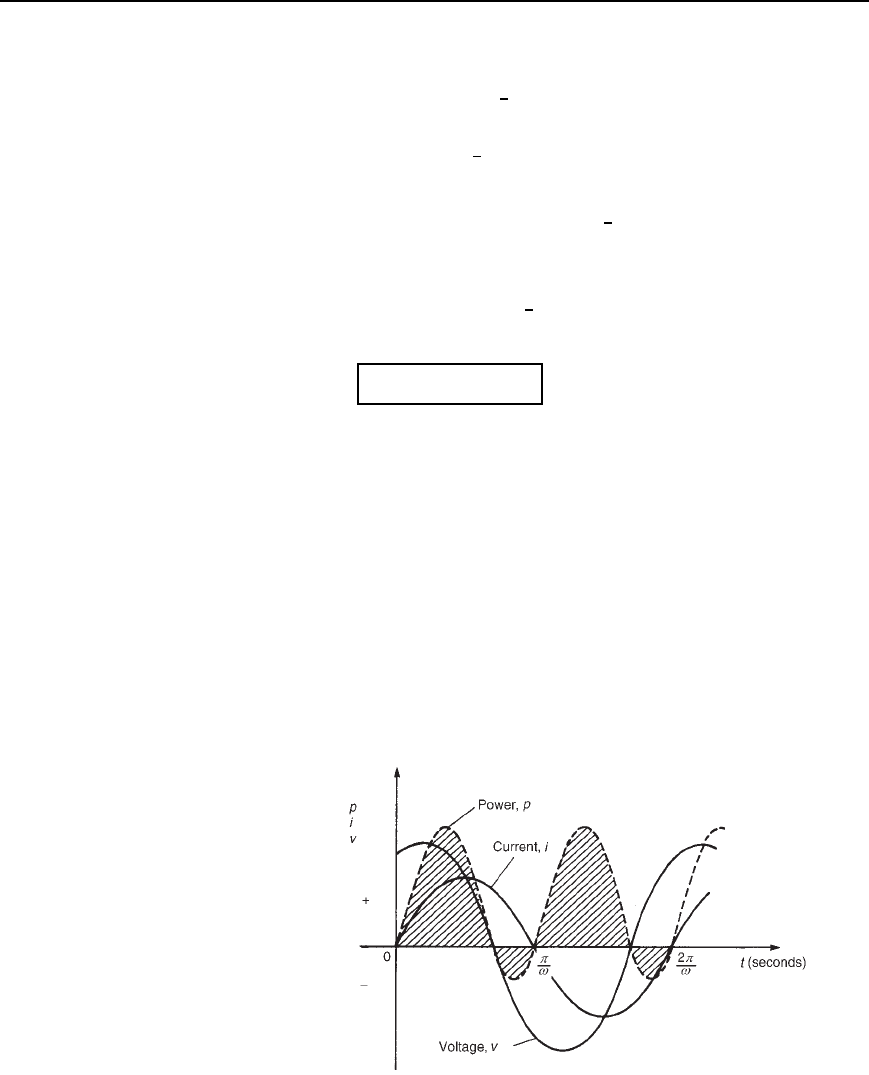
The waveforms of v, i and p, are shown in Figure 26.4 for an R–L circuit.

The waveform of power is seen to pulsate at twice the supply frequency.

The areas of the power curve (shown shaded) above the horizontal time

axis represent power supplied to the load; the small areas below the axis

represent power being returned to the supply from the inductance as the

magnetic ﬁeld collapses.

A similar shape of power curve is obtained for an R –C circuit, the

small areas below the horizontal axis representing power being returned

to the supply from the charged capacitor. The difference between the areas

above and below the horizontal axis represents the heat loss due to the

circuit resistance. Since power is dissipated only in a pure resistance, the

alternative equations for power, P D I

R, may be used, where I

is the

rms current ﬂowing through the resistance.

Figure 26.4 Power in a.c. circuit containing resistance and inductive

reactance

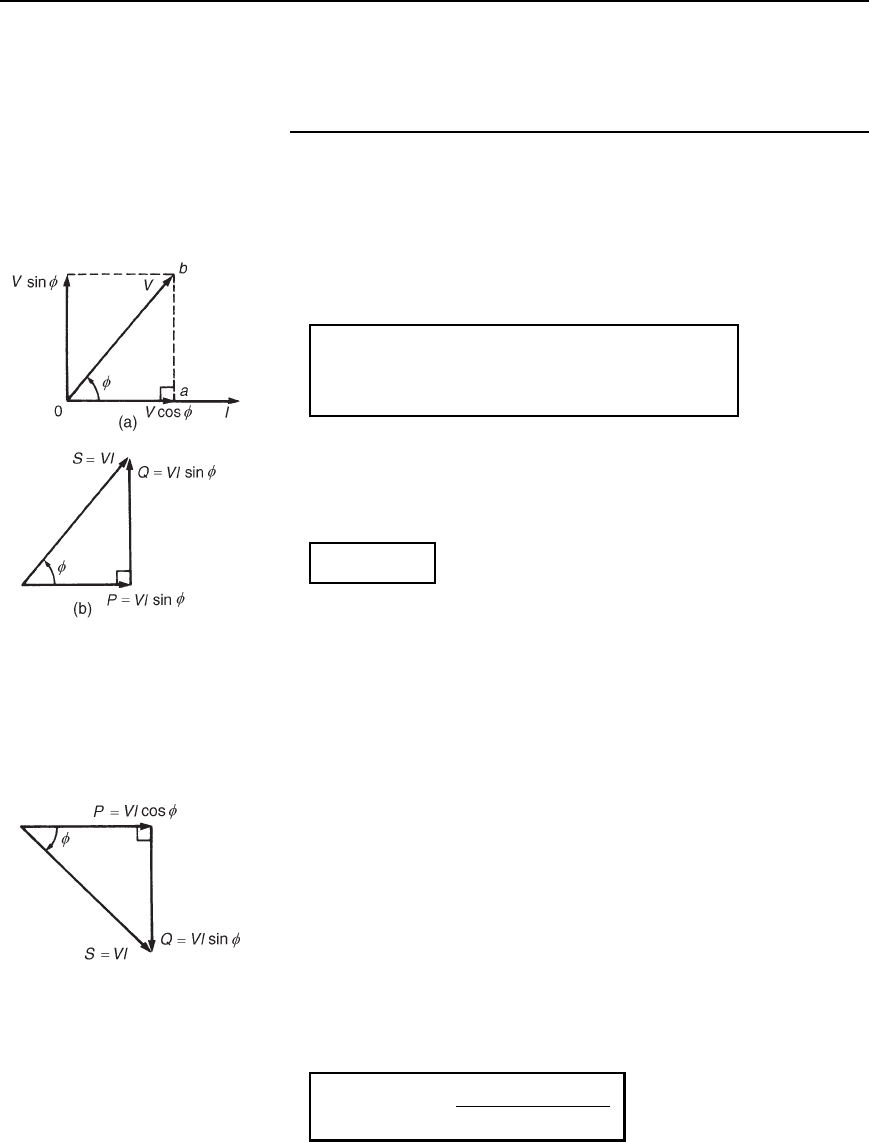
464 Electrical Circuit Theory and Technology

Summarizing, the average power P in a circuit containing resistance

and inductance and/or capacitance, whether in series or in parallel,

is given by P

= VI cosf or P = I

R .V ,I and I

being rms values).

26.3 Power triangle and

power factor

A phasor diagram in which the current I lags the applied voltage V

by angle  (i.e., an inductive circuit) is shown in Figure 26.5(a). The

horizontal component of V is V cos, and the vertical component of V is

V sin. If each of the voltage phasors of triangle Oab is multiplied by I,

Figure 26.5(b) is produced and is known as the ‘power triangle’. Each

side of the triangle represents a particular type of power:

True or active power P= VI cosf watts (W)

Apparent power S

= VI voltamperes (VA)

Reactive power Q

= VI sinf vars (var)

The power triangle is not a phasor diagram since quantities P, Q and S

are mean values and not rms values of sinusoidally varying quantities.

Superimposing the power triangle on an Argand diagram produces a

relationship between P, S and Q in complex form, i.e.,

S = P Y jQ

Figure 26.5 (a) Phasor

diagram, (b) Power triangle for

inductive circuit

Apparent power, S, is an important quantity since a.c. apparatus, such

as generators, transformers and cables, is usually rated in voltamperes

rather than in watts. The allowable output of such apparatus is usually

limited not by mechanical stress but by temperature rise, and hence by

the losses in the device. The losses are determined by the voltage and

current and are almost independent of the power factor. Thus the amount

of electrical equipment installed to supply a certain load is essentially

determined by the voltamperes of the load rather than by the power alone.

The rating of a machine is deﬁned as the maximum apparent power that

it is designed to carry continuously without overheating.

The reactive power, Q, contributes nothing to the net energy transfer

and yet it causes just as much loading of the equipment as if it did so.

Reactive power is a term much used in power generation, distribution and

utilization of electrical energy.

Inductive reactive power, by convention, is deﬁned as positive reactive

power; capacitive reactive power, by convention, is deﬁned as negative

reactive power. The above relationships derived from the phasor diagram

of an inductive circuit may be shown to be true for a capacitive circuit,

the power triangle being as shown in Figure 26.6.

Figure 26.6 Power triangle for

capacitive circuit

Power factor is deﬁned as:

power factor =

active power P

apparent power S

Power in a.c. circuits 465

For sinusoidal voltages and currents,

power factor D

VI cos

D cosf

(from the impedance triangle)

A circuit in which current lags voltage (i.e., an inductive circuit) is said

to have a lagging power factor, and indicates a lagging reactive power Q.

A circuit in which current leads voltage (i.e., a capacitive circuit) is said

to have a leading power factor, and indicates a leading reactive power Q.

26.4 Use of complex

numbers for

determination of power

Let a circuit be supplied by an alternating voltage V

˛, where

˛ D Vcos˛ C j sin˛ D V cos˛ C jV sin ˛ D a C jb 26.1

Let the current ﬂowing in the circuit be I

ˇ, where

ˇ D Icos ˇ C j sin ˇ D I cos ˇ C jIsin ˇ D c C jd 26.2

From Sections 26.2 and 26.3, power P D VI cos , where  is the angle

between the voltage V and current I. If the voltage is V

and the current

is I

, then the angle between voltage and current is ˛  ˇ

Thus power, P D VI cos˛  ˇ

From compound angle formulae, cos˛  ˇ D cos˛ cosˇ C sin˛ sinˇ.

Hence power, P D VI[cos ˛ cos ˇ C sin ˛ sin ˇ]

Rearranging gives P D V cos ˛I cos ˇ C V sin˛I sinˇ, i.e.,

P D ac C bd from equations (26.1) and (26.2)

Summarizing, if V

= .a Y jb/ and I = .c Y jd/, then

power, P = ac Y bd

26.3

Thus power may be calculated from the sum of the products of the real

components and imaginary components of voltage and current.

Reactive power, Q D VI sin˛  ˇ

From compound angle formulae, sin˛  ˇ D sin˛ cosˇ  cos˛ sinˇ.

Thus Q D VI[sin˛ cos ˇ  cos˛ sin ˇ]

Rearranging gives Q D V sin ˛I cosˇ  V cos ˛I sin ˇ i.e.,

Q D bc  ad from equations (26.1) and (26.2).

466 Electrical Circuit Theory and Technology

Summarizing, if V = .a Y jb/ and I = .c Y jd/, then

reactive power,

Q = bc − ad 26.4

Expressions (26.3) and (26.4) provide an alternative method of deter-

mining true power P and reactive power Q when the voltage and current

are complex quantities. From Section 26.3, apparent power S D P C jQ.

However, merely multiplying V by I in complex form will not give this

result, i.e. (from above)

S D VI D a C jbc C jd D ac  bd C jbc C ad

Here the real part is not the expression for power as given in equa-

tion (26.3) and the imaginary part is not the expression of reactive power

given in equation (26.4)

The correct expression may be derived by multiplying the voltage V

by the conjugate of the current, i.e. c  jd, denoted by I

. Thus

apparent power S

= VI

∗

D a C jbc  jd

D ac C bd C jbc  ad

i.e.,

S = P Y jQ

, from equations (26.3) and (26.4).

Thus the active and reactive powers may be determined if, and only

if, the voltage V is multiplied by the conjugate of current I. As stated

in Section 26.3, a positive value of Q indicates an inductive circuit, i.e.,

a circuit having a lagging power factor, whereas a negative value of

Q indicates a capacitive circuit, i.e., a circuit having a leading power

factor.

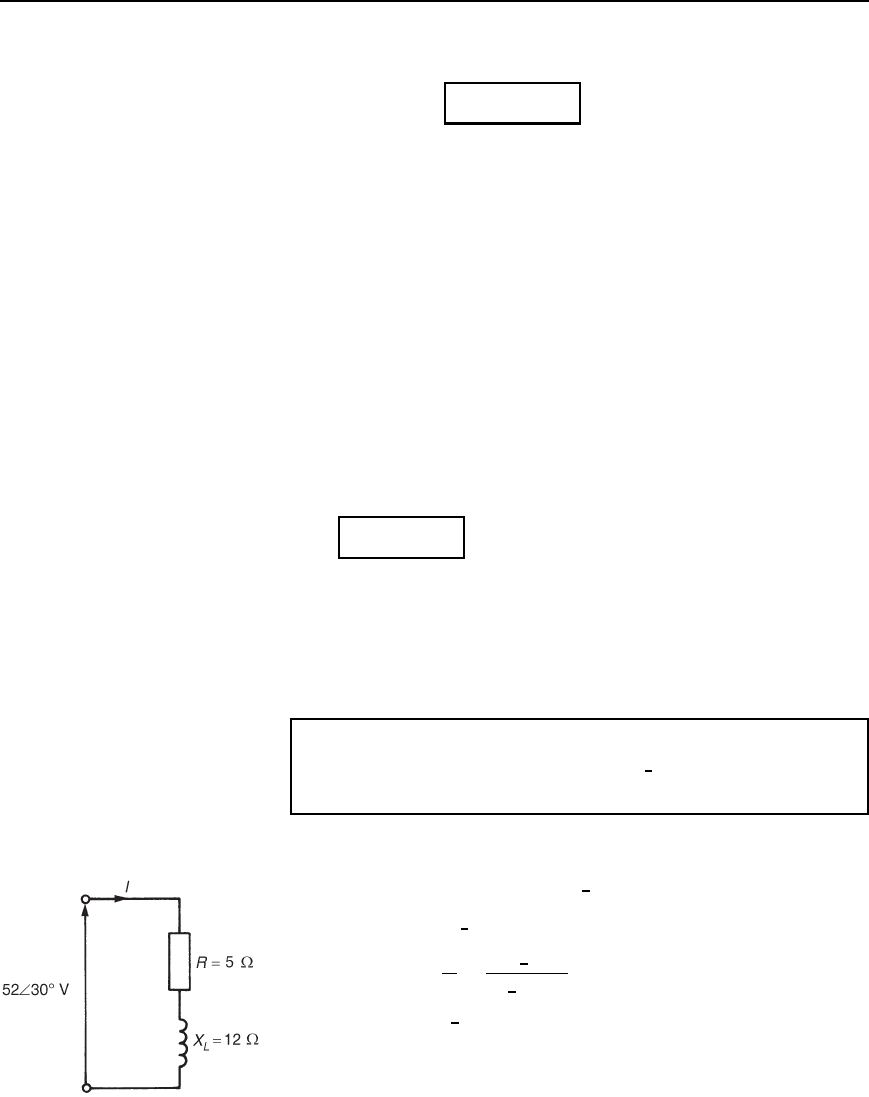
Problem 1. A coil of resistance 5  and inductive reactance 12 

is connected across a supply voltage of 52

volts. Determine the

active power in the circuit.

The circuit diagram is shown in Figure 26.7.

Impedance Z D 5 C j12 or 13

67.38



Voltage V D 52

Vor45.03 C j26.0V

Current I D

67.38

D 4

37.38

Aor3.18  j2.43A

There are three methods of calculating power.

Method 1. Active power, P D VI cos , where  is the angle

between voltage V and current I. Hence

Figure 26.7

Power in a.c. circuits 467

P D 524 cos[30

 37.38

] D 524 cos67.38

D 80 W

Method 2. Active power, P D I

R D 4

5 D 80 W

Method 3. Since V D 45.03 C j26.0Vand

I D 3.18  j2.43A, then active power,

P D 45.033.18 C 26.02.43

from equation (26.3), i.e.,

P D 143.2 63.2 D 80 W

Problem 2. A current of 15 C j8A ﬂows in a circuit whose

supply voltage is 120 C j200V. Determine (a) the active power,

and (b) the reactive power.

(a) Method 1. Active power P D 12015 C 2008,

from equation (26.3), i.e.,

P D 1800 C 1600 D 3400 W or 3.4kW

Method 2. Current I D 15 Cj8A D 17

28.07

Aand

Voltage V D 120 C j200V D 233.24

59.04

Angle between voltage and current D 59.04

 28.07

D 30.97

Hence power, P D VI cos D 233.2417 cos30.97

D 3.4 kW

(b) Method 1. Reactive power, Q D 20015  1208

from equation (26.4), i.e.,

Q D 3000  960 D 2040 var or

2.04 kvar

Method 2. Reactive power, Q D VI sin

D 233.2417 sin30.97

D 2.04 kvar

Alternatively, parts (a) and (b) could have been obtained directly, using

Apparent power, S D VI

D 120 C j20015  j8

D 1800 C 1600 C j3000  960

D 3400 C j2040 D P C jQ

from which, power P

= 3400 W and reactive power, Q = 2040 var