Bird J. Electrical Circuit Theory and Technology

Подождите немного. Документ загружается.

488 Electrical Circuit Theory and Technology

(d) Power factor of capacitor = cos D cos88.7

D 0.0227

(e) Loss angle, shown as υ in Figure 27.11, is given by

υ D 90

 88.7

D 1.3

Alternatively, loss angle υ D arctanωC

(see para (f), page 483)

D arctan



44.21



from (c) above,

i.e., υ D 1.3

Further problems on a.c. bridges may be found in Section 27.4 following,

problems 1 to 13.

27.4 Further problems

on a.c. bridges

1 A Maxwell-Wien bridge circuit ABCD has the following arm

impedances: AB, 250  resistance; BC, 2

µF capacitor in parallel

with a 10 k resistor; CD, 400  resistor; DA, unknown inductor

having inductance L in series with resistance R. Determine the values

of L and R if the bridge is balanced. [L D 0.20 H, R D 10 ]

2 In a four-arm de Sauty a.c. bridge, arm 1 contains a 2 k non-

inductive resistor, arm 3 contains a loss-free 2.4

µF capacitor, and

arm 4 contains a 5 k non-inductive resistor. When the bridge is

balanced, determine the value of the capacitor contained in arm 2.

µF]

3 A four-arm bridge ABCD consists of: AB — ﬁxed resistor R

;

BC—variable resistor R

in series with a variable capacitor C

;

CD—ﬁxed resistor R

; DA — coil of unknown resistance R and

inductance L. Determine the values of R and L if, at balance,

D 1k, R

D 2.5k, C

D 4000 pF, R

D 1k and the supply

frequency is 1.6 kHz. [R D 4.00 , L D 3.96 mH]

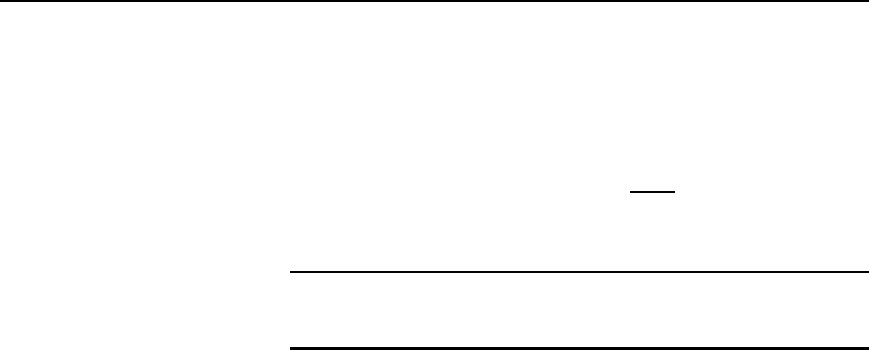
4 The bridge shown in Figure 27.12 is used to measure capacitance

and resistance R

. Derive the balance equations of the bridge

and determine the values of C

and R

when R

D R

, C

D 0.1 µF,

D 2k and the supply frequency is 1 kHz.

D 38.77 nF, R

D 3.27 k]

5 In a Schering bridge network ABCD, the arms are made up as

follows: AB—a standard capacitor C

; BC—a capacitor C

parallel with a resistor R

; CD — a resistor R

; DA — the capacitor

under test, represented by a capacitor C

in series with a resistor

. The detector is connected between B and D and the a.c. supply

is connected between A and C. Derive the equations for R

and

when the bridge is balanced. Evaluate R

and C

if, at balance,

D 1 nF, R

D 100 , R

D 1kand C

D 10 nF.

D 10 k, C

D 100 pF]

A.c. bridges 489

Figure 27.12 Figure 27.13

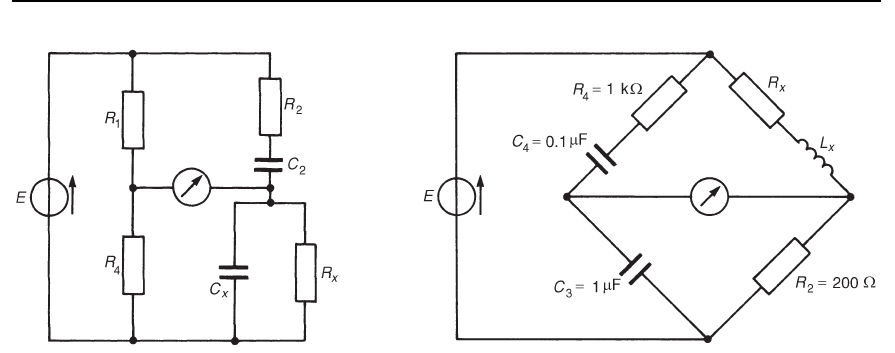
6 The a.c. bridge shown in Figure 27.13 is balanced when the values

of the components are shown. Determine at balance, the values of

and L

.[R D 2k, L

D 0.2H]

7 An a.c. bridge has, in arm AB, a pure capacitor of 0.4

µF; in arm BC,

a pure resistor of 500 ; in arm CD, a coil of 50  resistance and

0.1 H inductance; in arm DA, an unknown impedance comprising

resistance R

and capacitance C

in series. If the frequency of the

bridge at balance is 800 Hz, determine the values of R

and C

D 500 , C

D 4 µF]

8 When the Wien bridge shown in Figure 27.9 is balanced, the

components have the following values: R

D R

D 20 k, R

500 , C

D C

D 800 pF. Determine for the balance condition

(a) the value of resistance R

and (b) the frequency of the bridge

supply. [(a) 250  (b) 9.95 kHz]

9 The conditions at balance of a Schering bridge ABCD used to

measure the capacitance and loss angle of a paper capacitor are

as follows: AB — a pure capacitance of 0.2

µF; BC—a pure

capacitance of 3000 pF in parallel with a 400  resistance; CD—a

pure resistance of 200 ; DA—the capacitance under test which

may be considered as a capacitance C

in series with a resistance

. If the supply frequency is 1 kHz determine (a) the value of R

(b) the value of C

, (c) the power factor of the capacitor, and (d) its

loss angle. [(a) 3  (b) 0.4

µF (c) 0.0075 (d) 0.432

]

10 At balance, an a.c. bridge PQRS used to measure the inductance

and resistance of an inductor has the following values: PQ — a

non-inductive 400  resistor; QR— the inductor with unknown

inductance L

in series with resistance R

;RS—a3µF capacitor in

series with a non-inductive 250  resistor; SP —a 15

µF capacitor.

A detector is connected between Q and S and the a.c. supply is

connected between P and R. Derive the balance equations for R

and L

and determine their values. [R

D 2k, L

D 1.5H]

490 Electrical Circuit Theory and Technology

11 A 1 kHz a.c. bridge ABCD has the following components in its four

arms: AB — a pure capacitor of 0.2

µF; BC — a pure resistance of

500 ; CD—an unknown impedance; DA—a 400  resistor in

parallel with a 0.1

µF capacitor. If the bridge is balanced, determine

the series components comprising the impedance in arm CD.

[R D 59.41 , L D 37.6mH]

12 An a.c. bridge ABCD has in arm AB a standard lossless capacitor

of 200 pF; arm BC, an unknown impedance, represented by a loss-

less capacitor C

in series with a resistor R

; arm CD, a pure 5 k

resistor; arm DA, a 6  resistor in parallel with a variable capacitor

set at 250 pF. The frequency of the bridge supply is 1500 Hz. Deter-

mine for the condition when the bridge is balanced (a) the values of

and C

, and (b) the loss angle.

[(a) R

D 6.25 k, C

D 240 pF; (b) 0.81

]

13 An a.c. bridge ABCD has the following components: AB—a 1k

resistance in parallel with a 0.2

µF capacitor; BC—a 1.2 k

resistance; CD—a 750  resistance; DA — a 0.8

µF capacitor in

series with an unknown resistance. Determine (a) the frequency for

which the bridge is in balance, and (b) the value of the unknown

resistance in arm DA to produce balance.

[(a) 649.7 Hz (b) 375 ]

28 Series resonance and

Q-factor

At the end of this chapter you should be able to:

ž state the conditions for resonance in an a.c. series circuit

ž calculate the resonant frequency in an a.c. series circuit,

2

LC

ž deﬁne Q-factor as

and as

ž determine the maximum value of V

and V

COIL

and the

frequency at which this occurs

ž determine the overall Q-factor for two components in series

ž deﬁne bandwidth and selectivity

ž calculate Q-factor and bandwidth in an a.c. series circuit

ž determine the current and impedance when the frequency

deviates from the resonant frequency

28.1 Introduction

When the voltage V applied to an electrical network containing resistance,

inductance and capacitance is in phase with the resulting current I, the

circuit is said to be resonant. The phenomenon of resonance is of great

value in all branches of radio, television and communications engineering,

since it enables small portions of the communications frequency spectrum

to be selected for ampliﬁcation independently of the remainder.

At resonance, the equivalent network impedance Z is purely resistive

since the supply voltage and current are in phase. The power factor of a

resonant network is unity,(i.e., power factor D cos D cos0 D 1).

In electrical work there are two types of resonance— one associated

with series circuits,(which was introduced in Chapter 15), when the input

impedance is a minimum, (which is discussed further in this chapter),

and the other associated with simple parallel networks, when the input

impedance is a maximum (which is discussed in Chapter 29).

28.2 Series resonance

Figure 28.1 shows a circuit comprising a coil of inductance L and resis-

tance R connected in series with a capacitor C. The R–L –C series circuit

has a total impedance Z given by Z D R C jX

 X

) ohms, or Z D

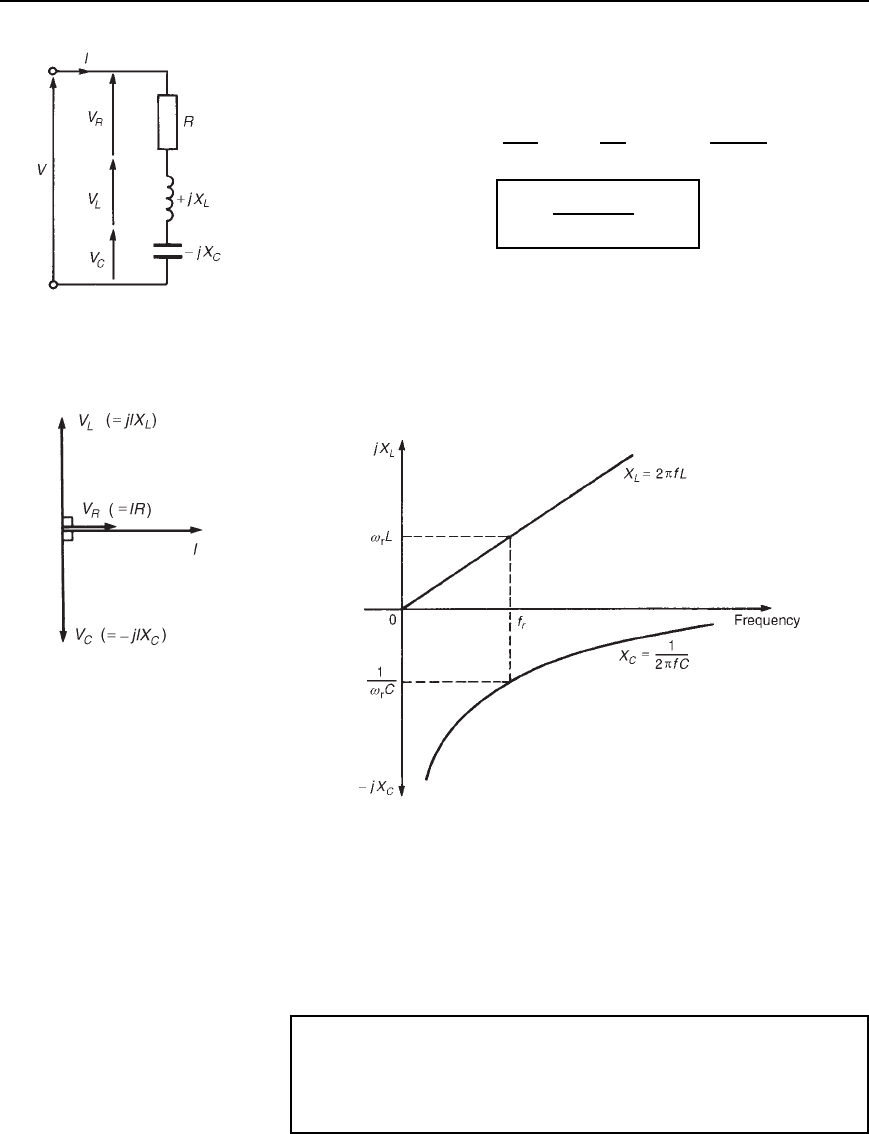
492 Electrical Circuit Theory and Technology

Figure 28.1 R  L  C series

circuit

R C jωL  1/ωC ohms where ω D 2f. The circuit is at resonance

when X

 X

 D 0, i.e., when X

D X

or ωL D 1/ωC. The phasor

diagram for this condition is shown in Figure 28.2, where jV

jDjV

Since at resonance ω

L D

, ω

and ω D

LC

Thus resonant frequency,

.LC/

hertz,

since ω

D 2f

Figure 28.2 Phasor diagram

jDjV

Figure 28.3 shows how inductive reactance X

and capacitive reactance

vary with the frequency. At the resonant frequency f

, jX

jDjX

Since impedance Z D R C jX

 X

 and, at resonance, X

 X

 D

0, then impedance Z

= R at resonance. This is the minimum value

possible for the impedance as shown in the graph of the modulus of

impedance, jZj, against frequency in Figure 28.4.

Figure 28.3 Variation of X

and X

with frequency

At frequencies less than f

, X

and the circuit is capacitive; at

frequencies greater than f

, X

and the circuit is inductive.

Current I D V/Z. Since impedance Z is a minimum value at resonance,

the current I has a maximum value. At resonance, current I D V/R.A

graph of current against frequency is shown in Figure 28.4.

Problem 1. A coil having a resistance of 10  and an inductance

of 75 mH is connected in series with a 40

µF capacitor across a

200 V a.c. supply. Determine at what frequency resonance occurs,

and (b) the current ﬂowing at resonance.

Series resonance and Q-factor 493

Figure 28.4 jZj and I plotted against frequency

(a) Resonant frequency,

2

LC

2



[75 ð 10

3

40 ð 10

6

]

i.e., f

= 91.9Hz

(b) Current at resonance, I D

200

D 20 A

Problem 2. An R–L –C series circuit is comprised of a coil of

inductance 10 mH and resistance 8  and a variable capacitor C.

The supply frequency is 1 kHz. Determine the value of capacitor

C for series resonance.

At resonance, ω

L D 1/ω

C, from which, capacitance, C D 1/ω

L

Hence capacitance C D

21000

10 ð 10

3



D 2.53 mF

Problem 3. A coil having inductance L is connected in series with

a variable capacitor C. The circuit possesses stray capacitance C

which is assumed to be constant and effectively in parallel with

the variable capacitor C. When the capacitor is set to 1000 pF

the resonant frequency of the circuit is 92.5 kHz, and when the

capacitor is set to 500 pF the resonant frequency is 127.8 kHz.

Determine the values of (a) the stray capacitance C

, and (b) the

coil inductance L.

494 Electrical Circuit Theory and Technology

For a series R–L –C circuit the resonant frequency f

is given by:

2

LC

The total capacitance of C in parallel with C

is given by C C C



At 92.5 kHz, C D 1000 pF. Hence

92.5 ð 10

2



[L1000 C C

10

12

]

1

At 127.8 kHz, C D 500 pF. Hence

127.8 ð 10

2



[L500 C C

10

12

]

2

(a) Dividing equation (2) by equation (1) gives:

127.8 ð 10

92.5 ð10

2



[L500 C C

10

12

]

2



[L1000 C C

10

12

]

i.e.,

127.8

92.5



[L1000 C C

10

12

]



[L500 C C

10

12

]





1000 C C

500 C C



where C

is in picofarads, from which,



127.8

92.5



1000 C C

500 C C

i.e., 1.909 D

1000 C C

500 C C

Hence 1.909500 C C

 D 1000 C C

954.5 C 1.909C

D 1000 C C

1.909C

 C

D 1000  954.5

0.909C

D 45.5

Thus stray capacitance C

D 45.5/0.909 D 50 pF

(b) Substituting C

D 50 pF in equation (1) gives:

92.5 ð10

2



[L1050 ð 10

12

]

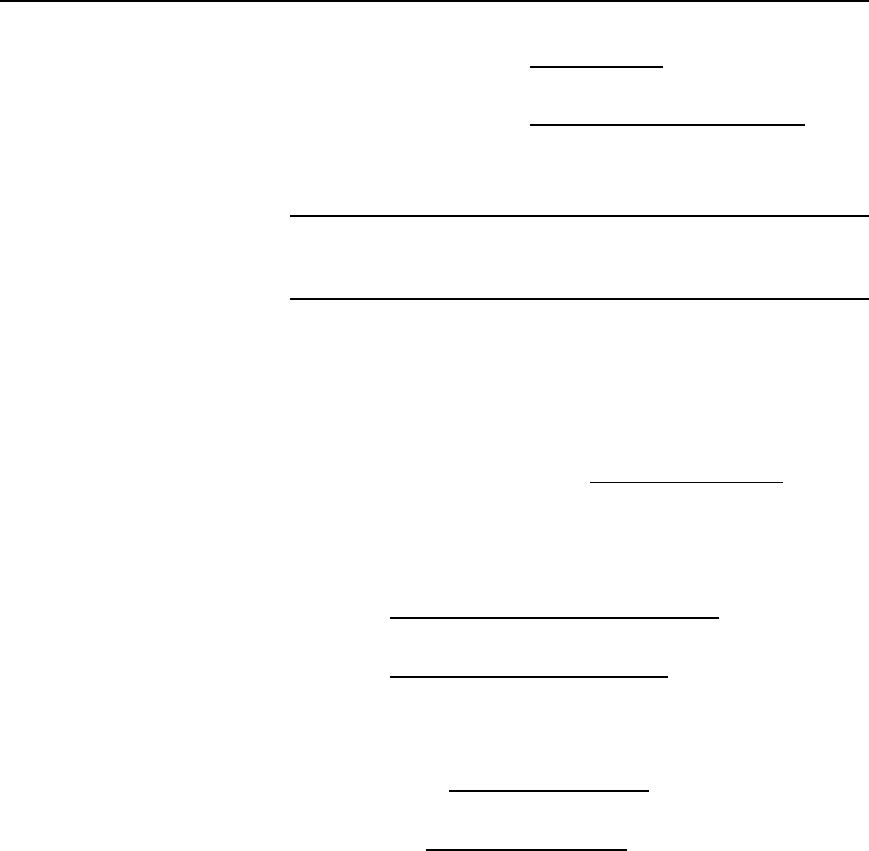
Series resonance and Q-factor 495

Hence 92.5 ð 10

ð 2

L1050 ð 10

12



from which, inductance L D

1050 ð 10

12

92.5 ð 10

ð 2

D 2.82 mH

Further problems on series resonance may be found in Section 28.8, prob-

lems 1 to 5, page 512

28.3 Q-factor

Q-factor is a ﬁgure of merit for a resonant device such as an L –C–R

circuit.

Such a circuit resonates by cyclic interchange of stored energy, accom-

panied by energy dissipation due to the resistance.

By deﬁnition, at resonance Q D 2



maximum energy stored

energy loss per cycle



Since the energy loss per cycle is equal to (the average power dissipated)

ð (periodic time),

Q D 2



maximum energy stored

average power dissipated ð periodic time



D 2



maximum energy stored

average power dissipated ð 1/f





since the periodic time T D 1/f

Thus Q D 2f



maximum energy stored

average power dissipated



i.e., Q D ω



maximum energy stored

average power dissipated



where ω

is the angular frequency at resonance.

In an L –C–R circuit both of the reactive elements store energy during

a quarter cycle of the alternating supply input and return it to the circuit

source during the following quarter cycle. An inductor stores energy in

its magnetic ﬁeld, then transfers it to the electric ﬁeld of the capacitor

and then back to the magnetic ﬁeld, and so on. Thus the inductive and

capacitive elements transfer energy from one to the other successively

with the source of supply ideally providing no additional energy at all.

Practical reactors both store and dissipate energy.

Q-factor is an abbreviation for quality factor and refers to the ‘good-

ness’ of a reactive component.

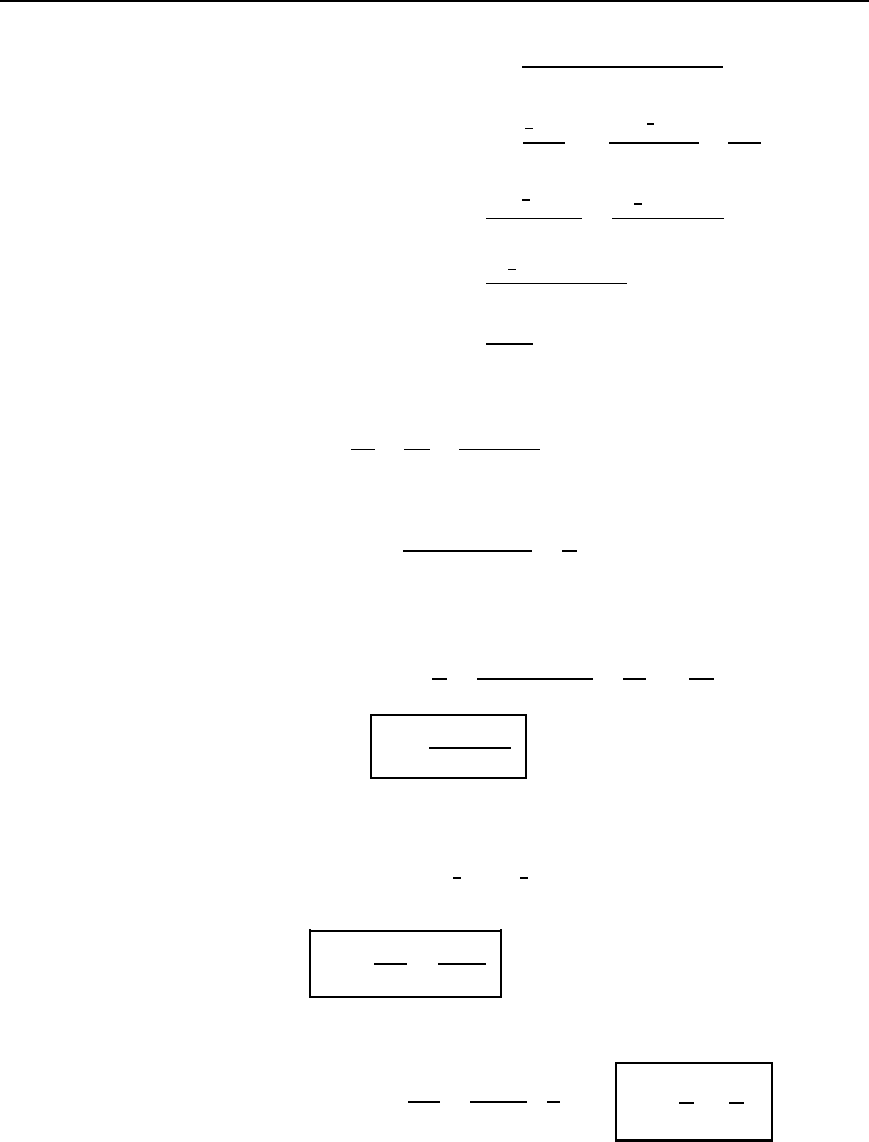
496 Electrical Circuit Theory and Technology

For an inductor, Q D ω



maximum energy stored

average power dissipated



D ω









I

2

28.1

For a capacitor Q D





I

2

CI



I

2

1/ω

C

I

2

i.e., Q D

28.2

From expressions (28.1) and (28.2) it can be deduced that

Q D

reactance

resistance

In fact, Q-factor can also be deﬁned as

Q-factor D

reactance power

resistance

where Q is the reactive power which is also the peak rate of energy

storage, and P is the average energy dissipation rate. Hence

Q-factor D

or I







i.e.,

Q =

reactance

resistance

In an R–L –C series circuit the amount of energy stored at resonance is

constant.

When the capacitor voltage is a maximum, the inductor current is zero,

and vice versa, i.e.,

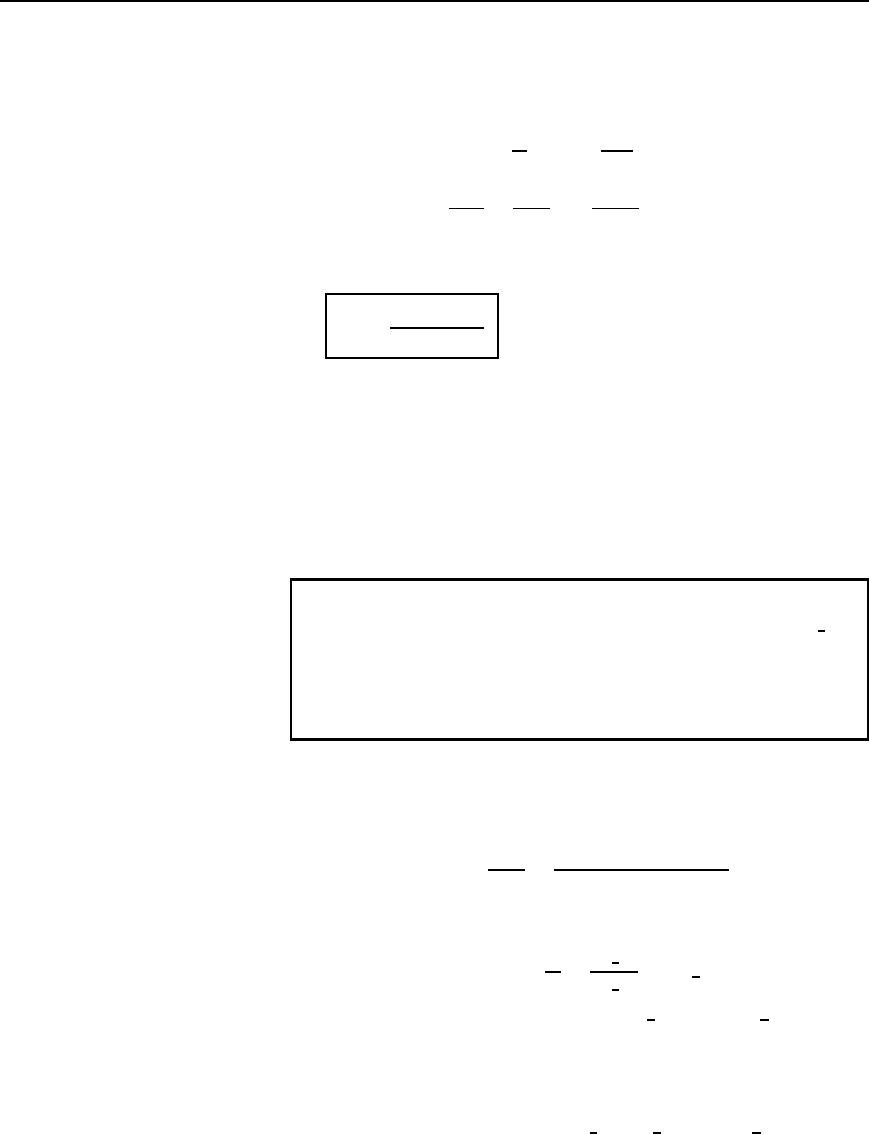
Thus the Q-factor at resonance, Q

is given by

28.3

However, at resonance ω

D 1/

LC

Hence Q

LC





i.e,







Series resonance and Q-factor 497

It should be noted that when Q-factor is referred to, it is nearly always

assumed to mean ‘the Q-factor at resonance’.

With reference to Figures 28.1 and 28.2, at resonance, V

D V

D IX

D Iω

L D





V D Q

and V

D IX

V/R





V D Q

Hence, at resonance, V

D V

D Q

.or V

The voltages V

and V

at resonance may be much greater than that

of the supply voltage V. For this reason Q is often called the circuit

magniﬁcation factor. It represents a measure of the number of times V

or V

is greater than the supply voltage.

The Q-factor at resonance can have a value of several hundreds. Reso-

nance is usually of interest only in circuits of Q-factor greater than about

10; circuits having Q considerably below this value are effectively merely

operating at unity power factor.

Problem 4. A series circuit comprises a 10  resistance, a 5 µF

capacitor and a variable inductance L. The supply voltage is 20

volts at a frequency of 318.3 Hz. The inductance is adjusted until

the p.d. across the 10  resistance is a maximum. Determine for

this condition (a) the value of inductance L, (b) the p.d. across each

component and (c) the Q-factor.

(a) The maximum voltage across the resistance occurs at resonance

when the current is a maximum. At resonance, ω

L D 1/ω

C,

from which

inductance L D

2318.3

5 ð 10

6



D 0.050 H or 50 mH

(b) Current at resonance I

D 2.0

p.d. across resistance, V

D I

R D 2.0

10 D 20

p.d. across inductance, V

D IX

D 2318.30.050 D 100 

Hence V

D 2.0

100

 D 200